Shanghai University
Article Information
- ZAINAL N. A., NAZAR R., NAGANTHRAN K., POP I.
- Unsteady flow of a Maxwell hybrid nanofluid past a stretching/shrinking surface with thermal radiation effect
- Applied Mathematics and Mechanics (English Edition), 2021, 42(10): 1511-1524.
- http://dx.doi.org/10.1007/s10483-021-2781-7
Article History
- Received Jun. 17, 2021
- Revised Aug. 14, 2021
2. Fakulti Teknologi Kejuruteraan Mekanikal dan Pembuatan, Universiti Teknikal Malaysia Melaka, Durian Tunggal 76100, Melaka, Malaysia;
3. Department of Mathematics, Babeş-Bolyai University, Cluj-Napoca R-400084, Romania
The non-Newtonian fluid has intrigued many scholars due to its enormous significance in nature and engineering systems, for instance, electronic chips, polymer depolarization, boiling, fermentation, composite processing, and bioengineering. In 1867, Maxwell[1] proposed a new kind of fluid, known as the Maxwell fluid. It is well-known that this type of fluid is the most basic subclass in the non-Newtonian fluid. The Maxwell fluid model estimates effects on relaxation time and is capable of estimating the shear-thinning liquid. This model also removes the complicated effects of shear-dependent viscosity, allowing researchers to focus solely on the role of fluid elasticity on boundary layer parameters[2]. Wang and Tan[3] investigated the stability performance of the Maxwell fluid model, and observed that the relaxation time boosted the system's instability.
The exploration of the Maxwell fluid model was broadened by Nadeem et al.[4] who incorporated the effects of nanoparticles in the non-Newtonian Maxwell fluid past a stretching sheet. The results showed that the inclusion of nanoparticles revealed a significant effect on the heat transfer and behaviors of the working fluid. The experimental work of Binetti et al.[5] proved that the sodium alginate (SA) exhibits the linear viscoelastic feature, which is an example of the Maxwell fluid. Next, Pawar and Sunnapwar[6] undertook an investigation on the heat transfer performance of non-Newtonian fluids (including the SA) in a helically coiled heat exchanger. Their study has provided the thermophysical properties data of the SA comprehensively. The SA has also been attempted as nanoparticles[7] and as base fluids[8], which benefits the applications in agriculture sectors.
In recent years, growing attention has been paid to classifying the nanoparticles' properties in a Newtonian hybrid nanofluid. However, limited studies have been reported on non-Newtonian hybrid nanofluid properties. Bahiraei et al.[9] performed an experimental study on the hydraulic and thermal features in a mini channel heat exchanger. The obtained results reflect a favorable outlook for using the non-Newtonian hybrid nanofluid in mini heat exchangers. Al-Rashed et al.[10] presented a numerical analysis of non-Newtonian hybrid nanofluid considering the thermodynamic properties in a microchannel heat sink. The results demonstrate that by increasing the concentration of nanoparticles, the thermal resistance decreases. Other studies in which non-Newtonian fluid was used to assess thermal efficiency can be reviewed here[11-13]. It is also worth mentioning here some good papers that discussed the respective problems[14-16].
Radiation parameters are one of the essential control factors for heat and fluid flow in the thermal system involving high temperatures. In particular, the effects of thermal radiation on the development of stable equipment, gas turbines, nuclear plants, satellites, missiles, and several complex conversion systems are very important[17-18]. Accordingly, Cess[19] was the first researcher who studied the heat transfer interaction between thermal reaction and free convection by employing the perturbation technique. The remarkable work has been widened by Arpaci[20] in a heated vertical plate towards a stagnant radiating gas. Since then, countless research works have been carried out on concerns with thermal radiation, such as Agbaje et al.[21], who performed a numerical analysis on the unsteady flow of Powell-Eyring nanofluid in the presence of thermal radiation and heat generation. The results revealed that the heat generation and thermal radiation parameters increased the thermal boundary layer thickness and fluid temperature.
In a nutshell, non-Newtonian fluid dynamics has gained much importance in recent decades due to its numerous practical applications. The typical fluid flow characteristics in the industry, such as polymeric liquids, biological fluids, and motor oils, can also be defined via the non-Newtonian fluid model. A review of the previously listed literature, however, addresses a variety of limitations and shortcomings. This research work aims to construct a mathematical model driven by the initial analysis to assess the numerical solutions of the unsteady flow in the Maxwell hybrid nanofluids with thermal radiation impact. The thermophysical characteristics of hybrid nanofluids are adopted from Takabi and Salehi[22] and Ghalambaz et al.[23]. It is important to note that an effective numerical procedure is crucial in solving this mathematical model. Hence, in this study, the bvp4c scheme in the MATLAB software is prompted to solve the resulting ordinary differential equations. This solver is built by utilizing a collocation approach with the fourth-order precision. By employing a pair of arbitrary initial guesses, the bvp4c solver can efficiently anticipate solutions. Also, the method described above has successfully provided multiple solutions in the current study. Moreover, previous literature demonstrated that the bvp4c solver is accurate in addressing boundary layer problems, as it is able to withstand and compete with other numerical methods such as the Keller-box method and the shooting method[24-26].
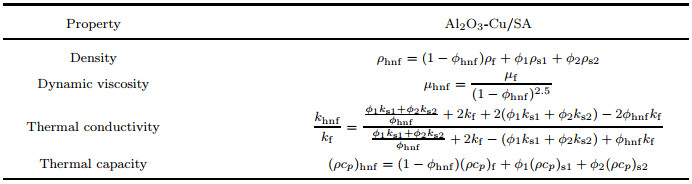
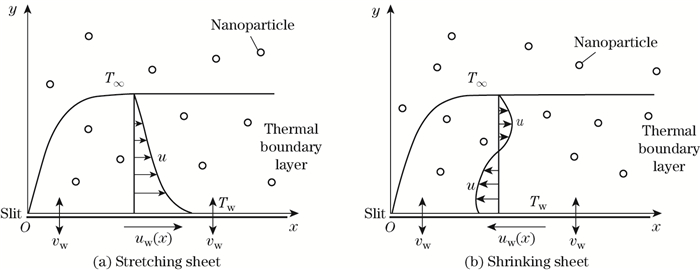
2 Mathematical modelIn this study, we deliberate the unsteady upper convected Maxwell hybrid nanofluid over a permeable stretching/shrinking sheet and heat transfer in two-dimensional laminar boundary layer flow, which starts at time t=0. The sheet moves with the non-uniform velocity uw (x, t), where (x, y) are the Cartesian coordinates, and the x- and y-axes are assigned along the surface and normal to it while the flow is at y≥ 0 (see Fig. 1). Also, the surface temperature Tw and ambient temperature T∞ are assumed to be constant. All these assumptions apply to geophysical problems such as double diffusive convection or salt finger evolution, reactor design in chemical processing, and turbidity currents[27-28]. Therefore, the governing equations of the respecting assumptions can be defined as[18, 29]
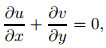
|
(1) |
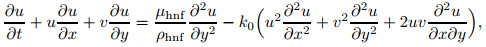
|
(2) |
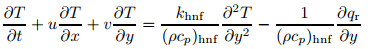
|
(3) |
|
| Fig. 1 Flow configuration |
|
|
subject to
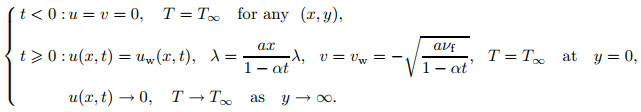
|
(4) |
Here, u is the velocity along the x-direction and v in the y-direction, vw (t) represents the mass flux velocity with vw (t) < 0 for suction and vw (t)>0 for injection, respectively, and α denotes the constant having dimension time t-1 such as (αt < 1, αt≥ 0), a denotes a positive constant, qr is the radiation, μhnf is the Al2O3-Cu/SA dynamic viscosity, khnf is the Al2O3-Cu/SA heat/thermal conductivity, ρhnf is the Al2O3-Cu/SA density, T is the temperature of Al2O3-Cu/SA, and (ρcp)hnf is the Al2O3-Cu/SA heat capacity. Table 1 shows the hybrid nanofluid thermophysical properties as defined by Takabi and Salehi[22] and Ghalambaz et al.[23]. Here, ϕ is the volume fraction of nanoparticles, ρf denotes the SA density, ρs is the hybrid nanoparticle density, kf and ks indicate the thermal conductivity of SA and hybrid nanoparticles, respectively, and finally cp is the heat capacity pressure. At the same time, the thermophysical properties of Cu, Al2O3 nanoparticles and also base fluid, SA, are demonstrated in Table 2 (see Ref. [30]).
The radiative heat flux qr is presented by the Rosseland[31] approximation,
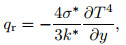
|
(5) |
where k* is the coefficient of mean absorption, and σ* is the Stefan-Boltzmann constant. We presume that within the flow, the temperature difference T4 can be extended in Taylor's series. Hence, enlarging T4 about T∞ while disregarding the terms of the higher-order, we obtain
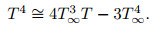
|
(6) |
Thus,
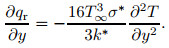
|
(7) |
Substituting Eq. (7) into Eq. (3), we get
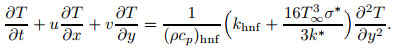
|
(8) |
By considering the following dimensionless variables[29]:
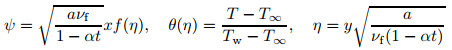
|
(9) |
with the stream function ψ, which is defined as 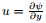
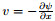
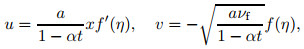
|
(10) |
so that
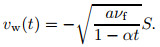
|
(11) |
In the above equation, S is a parameter of the mass flux, where S=0 denotes an impermeable surface, and S < 0 and S>0 correspond to injection and suction, respectively. Substituting (9) into Eqs. (2) and (8), we get the following ordinary (similarity) differential equations:
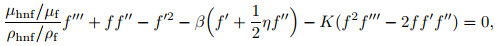
|
(12) |
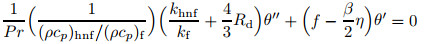
|
(13) |
subject to
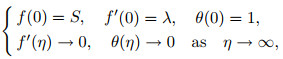
|
(14) |
where primes denote differentiation with respect to η, Pr=νf/αf is the Prandtl number, λ is the constant stretching/shrinking parameter with λ >0 for the stretching sheet, λ < 0 for the shrinking sheet, and λ =0 for the static sheet. The unsteadiness parameter is defined by β =a/α with β < 0 indicating the decelerating flows, and β >0 indicating the accelerating flow, while β =0 indicates the steady-state flow, and K=ak0 is the Maxwell parameter. Now, we describe Cf (skin friction coefficient) and Nux (local Nusselt number) as follows:
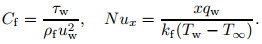
|
(15) |
We note that τw and qw are the shear stress and the heat flux from the plate, respectively. Thus, we have
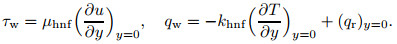
|
(16) |
Utilizing Eqs. (9) and (16), we get
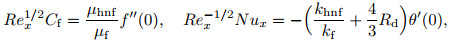
|
(17) |
where Rex=uw(x, t)x/νf is the local Reynolds number, and Rd=4σ* T∞3/(kfk*) is the radiation parameter.
3 Stability analysisSince several solutions in the boundary value problem (12)-(13) have been demonstrated, an examination of solution stability is carried out. This technique has been frequently adopted by a number of researchers due to its validity[32-34]. By perceiving the efforts of Merkin[35] and Merrill et al.[36], we instigate a new transformation variable τ under the unsteady-state query in the following way[37-38]:
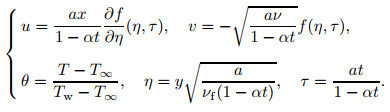
|
(18) |
Substituting Eq. (15) into Eqs. (12)-(13), the following equations are secured:
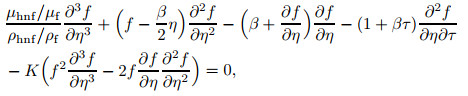
|
(19) |
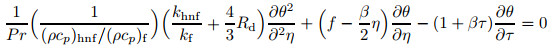
|
(20) |
with respect to
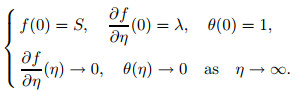
|
(21) |
To scrutinize the steady flow solutions stability, where f(η)=f0 (η) and θ (η)=θ0 (η), we describe f(η, τ)=f0(η)+e-ωτF(η) and θ (η, τ)=θ0 (η)+e-ωτH(η), which is developed by Weidman et al.[39]. Here, F(η) and H(η) are relatively small to f0 (η) and θ0 (η), while ω is the undetermined eigenvalue parameter. The eigenvalue problem (19)-(20) leads to an infinite number of eigenvalues ω1 < ω2 < ω3⋯ that disclose a steady flow and initial deterioration when ω1 is positive. On the other hand, once ω1 is negative, an initial development of perturbations will be discovered. This finding exposes the occurrence of unstable flow. By substituting Eq. (21) into Eqs. (19)-(21), the equations below are generated,
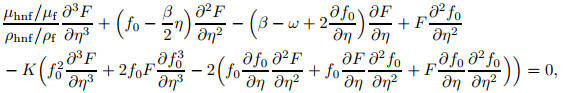
|
(22) |
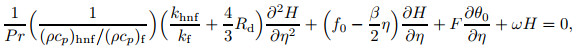
|
(23) |
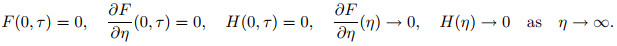
|
(24) |
Now, we implement the steady-state flow solutions f0(η) and θ0 (η) via τ→0. As a result, the linearized eigenvalue problem is determined as follows:
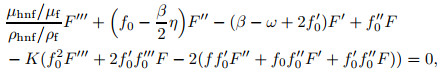
|
(25) |
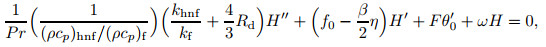
|
(26) |
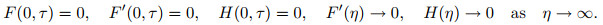
|
(27) |
The possible eigenvalues could be deliberated via relaxing a boundary condition[40], where the value of F'(η)→0 is fixed as η→∞, and thus the linearized eigenvalue problems (25)-(26) are exposed as F"(0)=1 when ω1 is set up.
4 Interpretation of resultsThe resulting ordinary differential equations presented in Eqs. (12)-(14) are clarified in the MATLAB software[41] by utilizing the bvp4c method. In this technique, the essential approximation of boundary layer thickness is critical while discovering multiple solutions. Before achieving the required outcome, several attempts need to be performed in offering a significant initial prediction. Further, the reliability of the findings is measured with Sharidan et al.[42], who employed the Keller-box method and Chamka et al.[43], together with Madhu et al.[29], who utilized the finite-difference method. By establishing an explicit agreement with previous literature, the significance of the existing numerical approach, i.e., the bvp4c function, is undeniable as accessible in Table 3. Thus, we suggest that the proposed conceptual model thoroughly examine heat transfer and fluid flow activity with considerable certainty.

|
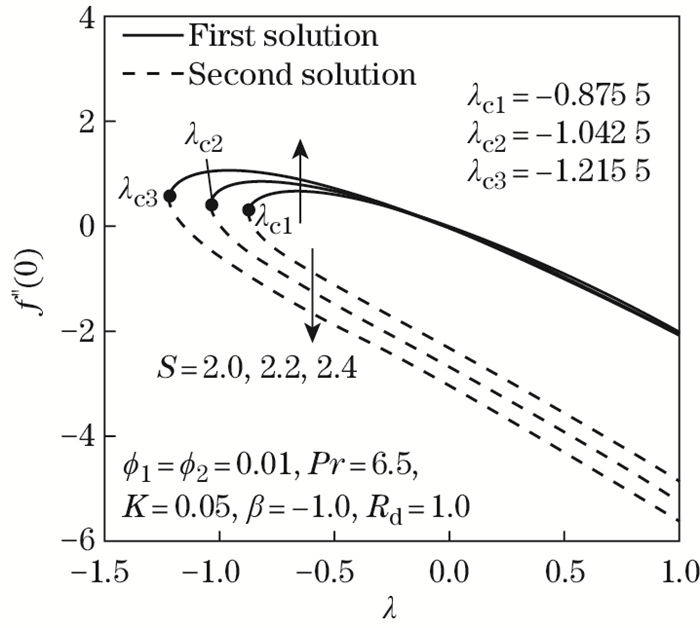
Figures 2-15 unveil the existence of the dual solution for preferred proportions of the controlling parameters when the stretching/shrinking parameter (λ) is varied. In the entire study, the dual solutions are seen as the sheet shrinks (λ < 0) within a certain limit of a critical point, i.e., λc. When λ < λc, no solution is noticed as it expresses the separation of the boundary layer. It is also worth noting here that the counter-argument of which solutions ultimately take place in a real-life application depends on flow stability, which demands comprehensive examination. Furthermore, certain limiting parameters are utilized to assure the accuracy of the outputs, and they are fixed to the extents listed here; 0.0≤ ϕ2 ≤ 0.3, 2.0≤ S≤ 2.4, 0.03≤ K≤ 0.08, -0.5≤ β ≤ -1.5, and 1≤ Rd≤ 3. During the analytical execution of this investigation, the Prandtl number is assigned to 6.5, omitting any similarities with previous arguments.
|
| Fig. 2 f"(0) as opposed to λ by S=2.0, 2.2, 2.4 |
|
|
|
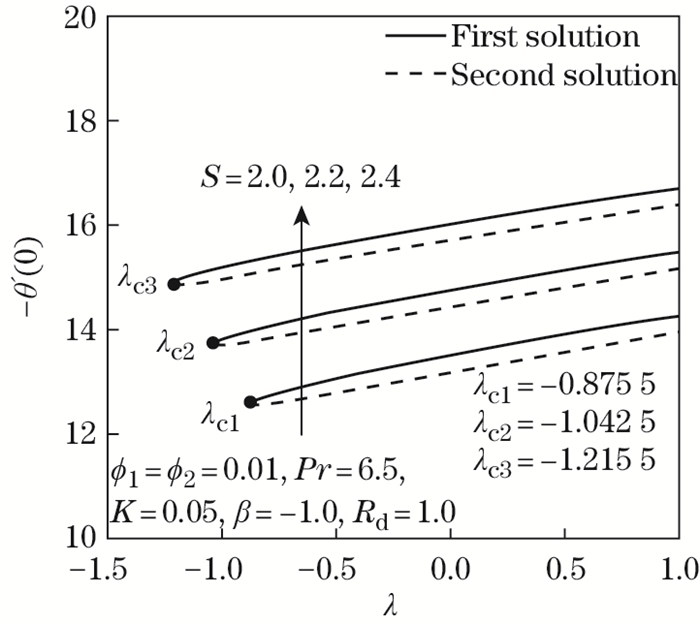
| Fig. 3 -θ'(0) as opposed to λ by S=2.0, 2.2, 2.4 |
|
|
|
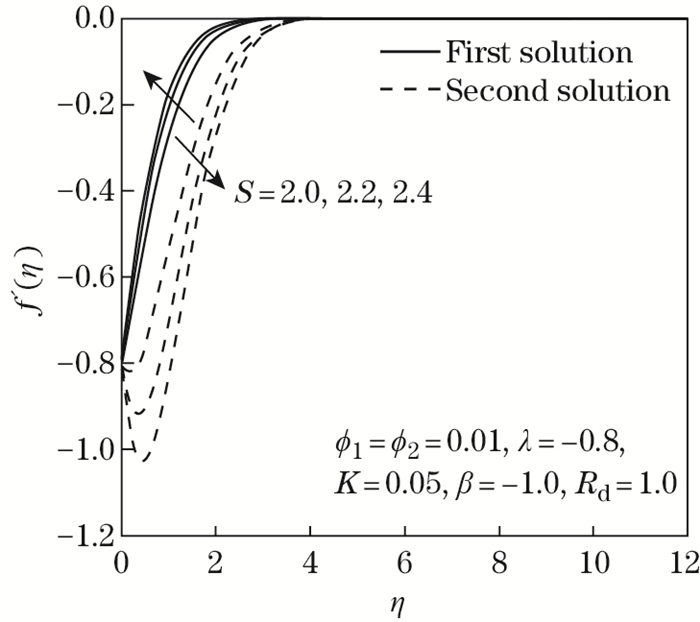
| Fig. 4 f'(η) as opposed to η by S=2.0, 2.2, 2.4 |
|
|
|
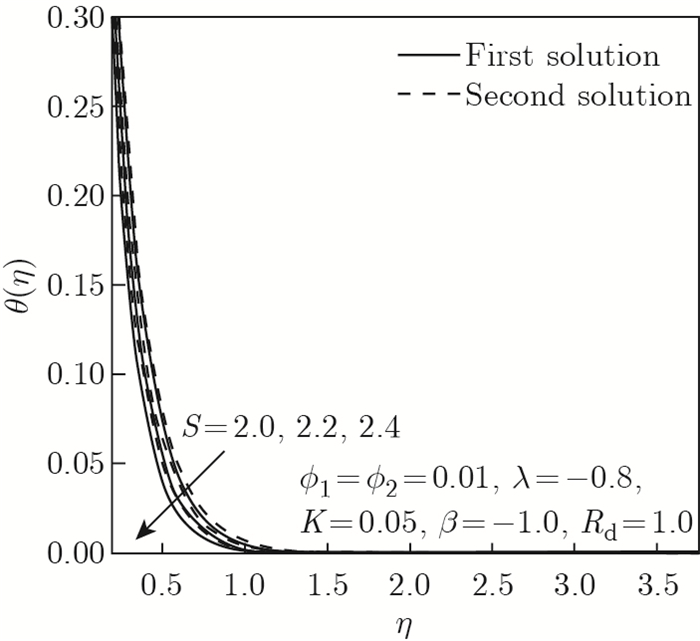
| Fig. 5 θ (η) as opposed to η by S=2.0, 2.2, 2.4 |
|
|
|
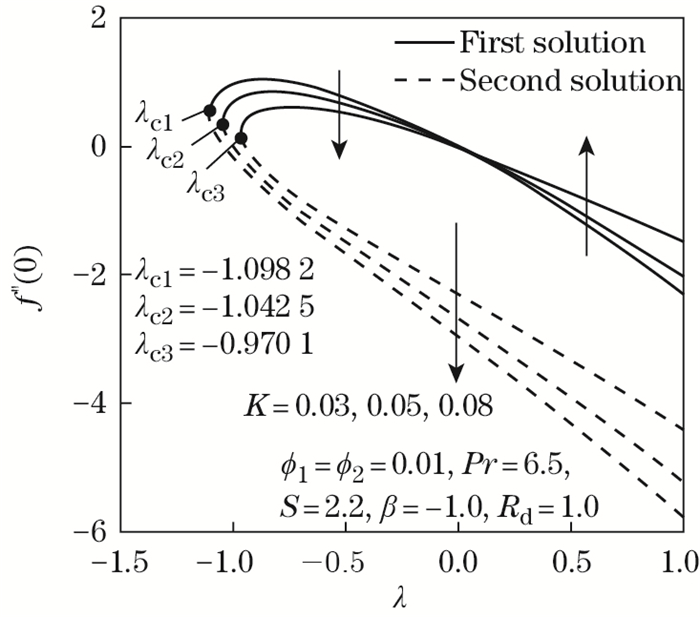
| Fig. 6 f"(0) as opposed to λ by K=0.03, 0.05, 0.08 |
|
|
|
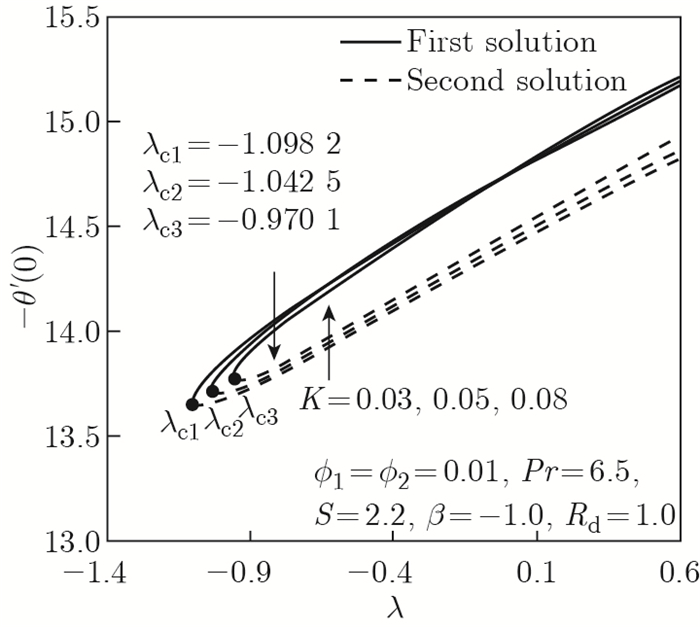
| Fig. 7 -θ'(0) as opposed to λ by K=0.03, 0.05, 0.08 |
|
|
|
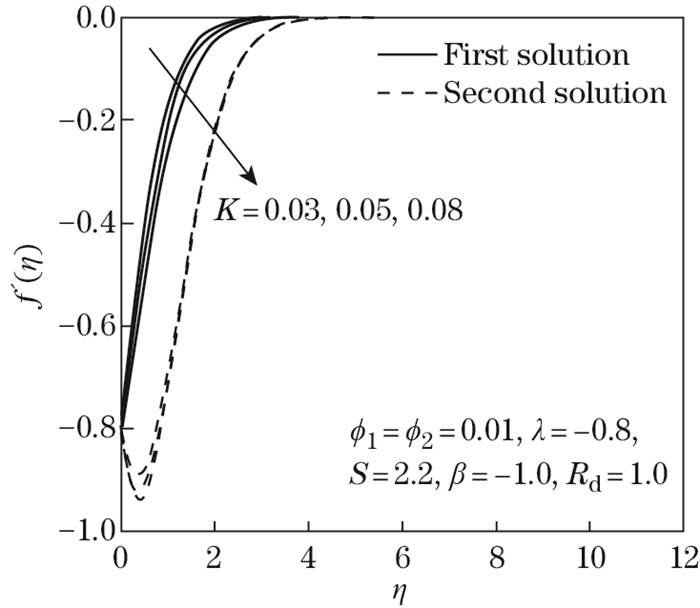
| Fig. 8 f'(η) as opposed to η by K=0.03, 0.05, 0.08 |
|
|
|
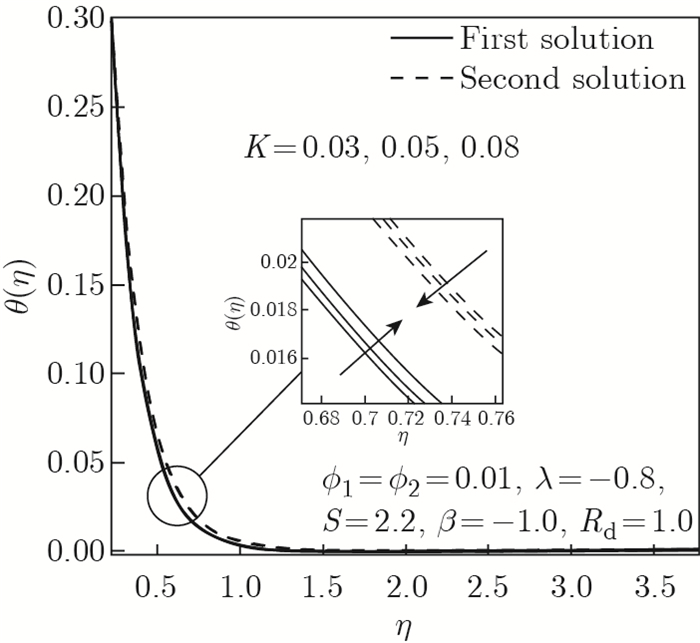
| Fig. 9 θ (η) as opposed to η by K=0.03, 0.05, 0.08 |
|
|
|
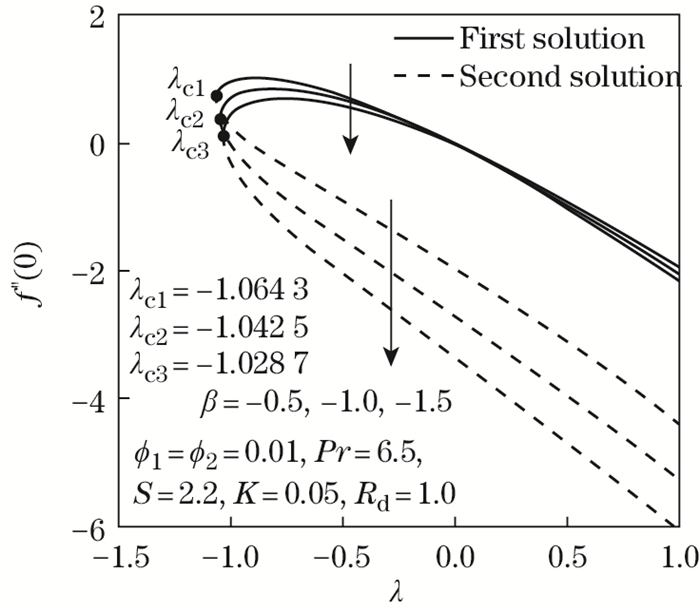
| Fig. 10 f"(0) as opposed to λ by β=-0.5, -1.0, -1.5 |
|
|
|
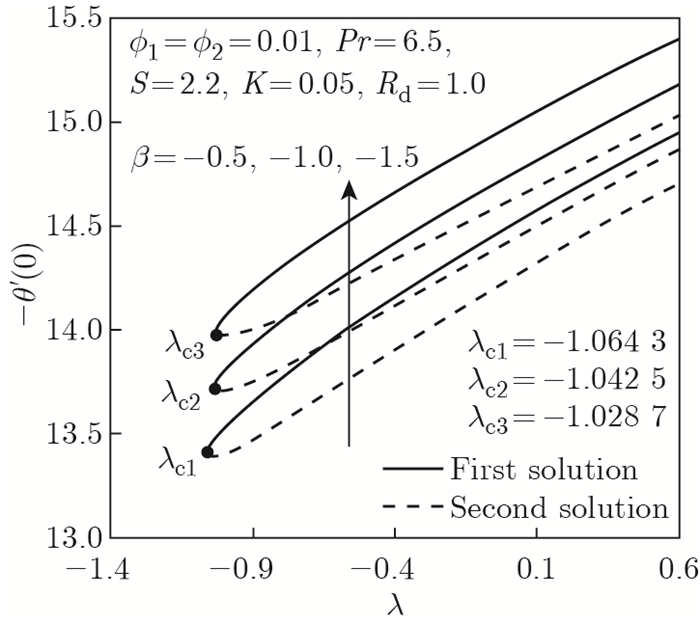
| Fig. 11 -θ'(0) as opposed to λ by β=-0.5, -1.0, -1.5 |
|
|
|
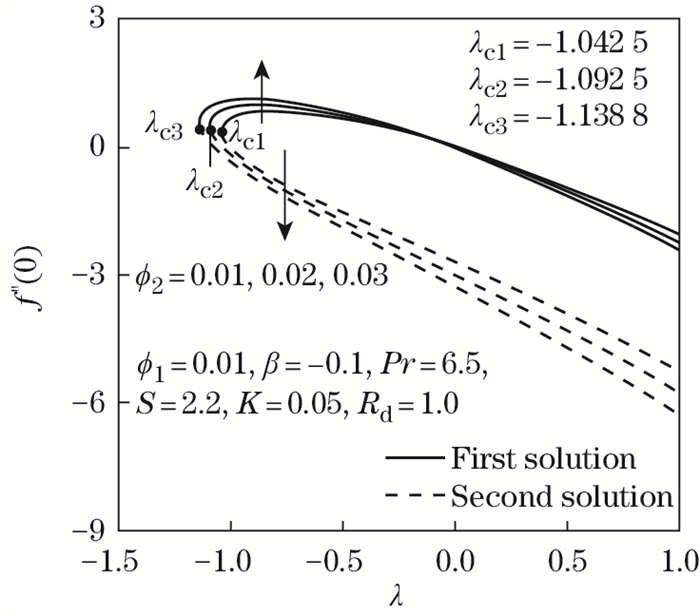
| Fig. 12 f"(0) as opposed to λ by ϕ2 =0.01, 0.02, 0.03 |
|
|
|
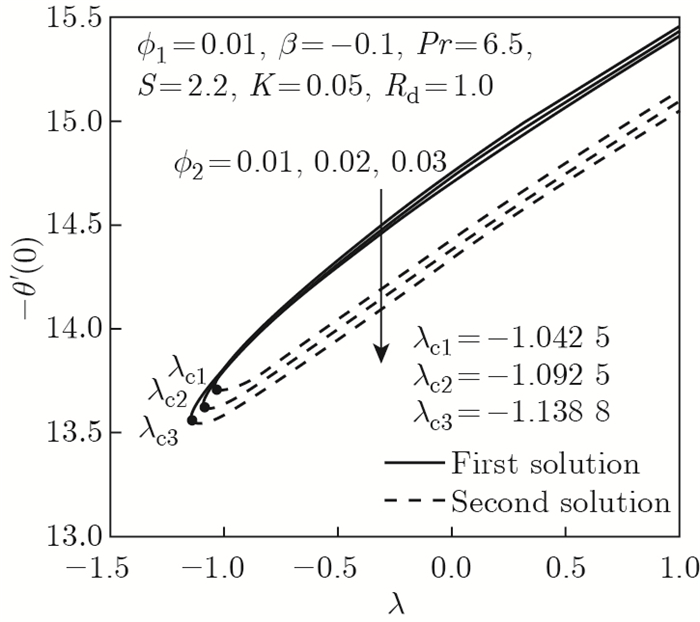
| Fig. 13 -θ'(0) as opposed to λ by ϕ2 =0.01, 0.02, 0.03 |
|
|
|
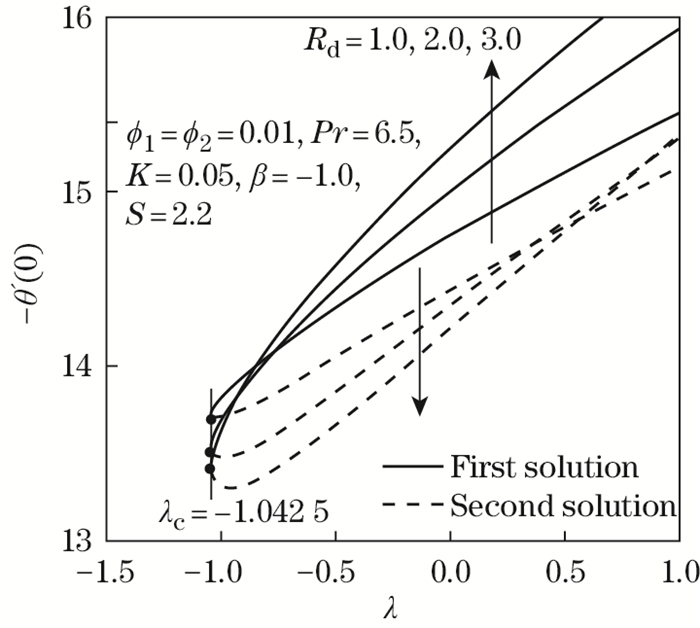
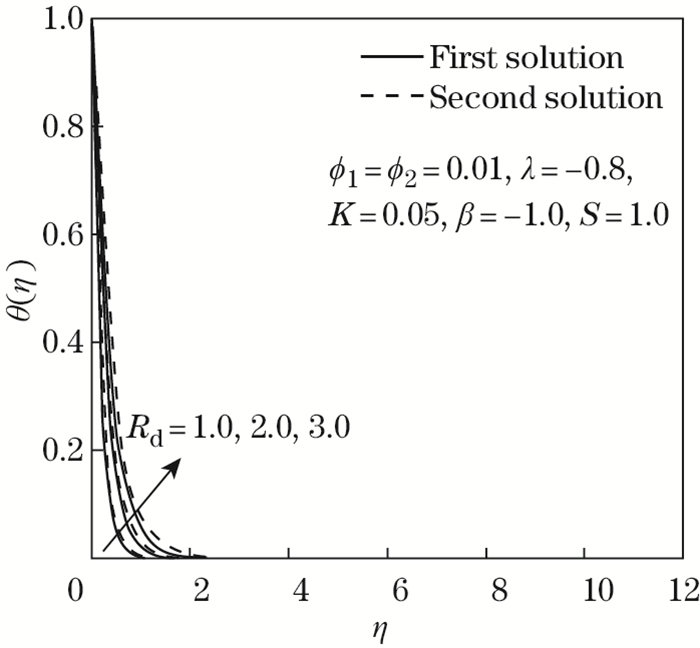
| Fig. 14 -θ'(0) as opposed to λ by Rd=1.0, 2.0, 3.0 |
|
|
|
| Fig. 15 θ (η) as opposed to η by Rd=1.0, 2.0, 3.0 |
|
|
Figures 2 and 3 expose the effects of assorted values in the suction parameter S toward λ past a stretching/shrinking surface. The characteristic of f"(0) in Al2O3-Cu/SA is described in Fig. 2, and it indicates that, in the first solution, an improvement in S would substantially upsurge f"(0). By comparison, another solution reveals a declining tendency of f"(0) with the addition of S. The occurrence of suction on a stretching/shrinking sheet potentially promotes the stabilization of the boundary layer. Besides, the suction parameter lowers the body pressure in such a decelerating flow, thereby augmenting the velocity gradient and reducing the thickness of the stretching/shrinking sheet boundary layer by evacuating the fluid with low momentum alongside the surface. This is proven in Fig. 4, which displays the velocity profile f'(η) with multiple values of S. Meanwhile, the first and second solutions provide an enhancement in -θ'(0) as S escalates through the Al2O3-Cu/SA stretching/shrinking surface, which is clarified in Fig. 3. It is worth noting that the suction action allows Maxwell hybrid nanofluid particles to occupy the surface as it stretches or shrinks and boost up the rate of heat transfer physically. The temperature distribution profile θ (η) confirms this argument by showing a downward trend in both solutions, where suction is imposed in the stretching/shrinking sheet, as displayed in Fig. 5. In general, the momentum and temperature distribution profiles f'(η) and θ (η) satisfy the far-field boundary conditions (14) whenever η∞ =12 is executed.
Figures 6 and 7 inaugurate the effects of Maxwell parameter K on f"(0) and -θ'(0) in the Maxwell hybrid nanofluid, respectively. The consequence of rising K values is to reduce the velocity field and thereby decrease the thickness of the boundary layer, as presented in Fig. 8. From a physical perspective, fluid tends to rest when the shear stress is eliminated. This phenomenon can be observed in a variety of polymeric liquids that defy the Newtonian fluid model. Also, a high value of the Maxwell parameter may create a retarding force in the flow between two adjacent layers. This leads to a decline in the velocity and the thickness of the boundary layer, which can be seen in Fig. 8. Figure 7 displays a diminishing response of -θ'(0) when K varies in the first solution. Concisely, the rate of heat transfer decreases as K improves in a Maxwell hybrid nanofluid. This observation suggests that the addition of the Maxwell parameter in the boundary layer may minimize the heat transfer rate of the thermal boundary layer, thus increasing the fluid's temperature. This is in accord with the temperature profile trend at the stretching/shrinking surface of the Maxwell hybrid nanofluid Al2O3-Cu/SA as disclosed in Fig. 9. Figure 9 confirms that by extending the Maxwell parameter value, the temperature profile increases since the thickening of the thermal boundary layer enhances the elasticity stress parameter. Additionally, improving the value of K in the Maxwell hybrid nanofluid is proven to boost up characteristics of the first solution; however, diminishes in other solution of the temperature distribution profile.
The effects of the unsteadiness parameter β toward λ when β shifts from -0.5 to -1.5 are demonstrated in Figs. 10-11. The Maxwell hybrid nanofluid Al2O3-Cu/SA characteristic is depicted in fig. 10 with respect to f"(0) when β is reduced. the reduction of β leads to the expansion of the boundary layer thickness and subsequently declines the velocity gradient, and hence f"(0) diminishes. the presence of the nanoparticle volume fraction could also initiate the decline of f"(0) because of the rise in the maxwell hybrid nanofluid viscosity. moreover, according to the generated results in fig. 11, -θ'(0) is increased in both solutions as β decreases. based on the present results, the authors can deduce that a reduction value of the unsteadiness parameter promotes the rise of the heat transfer rate significantly. even so, if multiple control parameters are taken into account, the authors would also like to claim that those effects may vary.
Figures 12-13 present the responses of f"(0) and -θ'(0) in the Maxwell hybrid nanofluid when ϕ2=0.01, 0.02, and 0.03. Figure 12 expresses that an augmentation in the nanoparticle volume fraction ϕ2 (Cu) is proven to intensify the f"(0) values. The intensification of ϕ2 improves the Maxwell hybrid nanofluid viscosity, which successively boosts the fluid velocity. While f"(0) increases, the frictional drag exerted increases, potentially slowing the separation of the boundary layer as the surface shrinks. In contrast, the downward trend of f"(0) is revealed when ϕ2 improves, and the value of reduced skin friction coefficient progressively becomes negative. The negative value of f"(0) elucidates that the Maxwell hybrid nanofluid imposes the drag force away from the sheet. Figure 12 also emphasizes that when λ=0 (static sheet), f"(0)=0, which reflects a lack of frictional drag on the surface of the static sheet. Figure 13 depicts the behavior of declining thermal performance or -θ'(0) towards a shrinking sheet, and this behavior can be seen in every solution. In other words, as ϕ2 rises, the heat transmission performance decreases. Theoretically, as the mass of the Maxwell hybrid nanoparticles increases, the temperature of the sheet rises; as a result, the efficiency of thermal conductivity drops, affecting the performance of heat transfer. This could be due to radiation parameter effects that raising the temperature across the surface and disrupting nanoparticle interactions, result in lowering thermal conductivities.
The effects of the radiation parameter Rd in the Maxwell hybrid nanofluid Al2O3-Cu/SA are shown in Figs. 14 and 15. Figure 14 presents the variants of -θ'(0) for several values of Rd where Rd=1.0, 2.0, and 3.0, while Fig. 15 displays the temperature profile distribution θ (η). The thermal radiation parameter is discovered to increase the temperature profile distribution. Substantially, -θ' (0) boosts when the thermal radiation parameter is intensified attributing to the conversion of thermal energy. This is due to the development and transmission of more heat into the flow, which helps increase the momentum boundary layer thickness. The same findings were found in the preceding literature[18]. On another note, Fig. 15 displays the increment of θ (η) when Rd improves to the extent that the energy conversion rate over the non-Newtonian Maxwell hybrid nanofluid is enlarged. The observations in the previous analysis (see Ref. [44]) indicated the same effects as the current findings. Up to now, it has been demonstrated that the influence of thermal radiation can raise the temperature of a Maxwell hybrid nanofluid in a stretching/shrinking surface prior to the listed condition.
A stability analysis was further conducted by utilizing the bvp4c application in the MATLAB software. The smallest eigenvalues ω1 for certain values of λ when ϕ1=ϕ2=0.01, S=2.2, K=0.05, β =1.0, Rd=1.0, and Pr=6.5 are given in Table 4. The first solution is usually denoted as reliable because it fulfils the far-field boundary condition. By conducting a stability analysis, we are able to confirm the accurate and reliable solutions convincingly. In the stability analysis procedure, the smallest eigenvalue ω1 indicates the characteristics of the dual solutions. When ε1 is positive, the flow is considered stable since the solutions comply with the stabilizing property where an initial decay is permitted. Meanwhile, when ω1 appears negative, the flow is represented unreliable as it evokes an initial extension of disturbances. The first solution is found to be reliable, while the alternative solution is unreliable, as witnessed in Table 4.
A mathematical analysis of the unsteady Maxwell hybrid nanofluid over a stretching/shrinking surface with the impact of thermal radiation is validated. The Maxwell hybrid nanofluid is chosen as the operating fluid since this model is proposed to describe the behavior of viscoelastic fluids and succeed in modeling the polymeric liquids. The present work is an example of a numerical approach to a thermal extrusion manufacturing process, such as drawing plastic films or extrusion of a polymer sheet from a dye. The findings indicate that the existence of dual solutions across the Maxwell hybrid nanofluid Al2O3-Cu/SA flow is factual in specific controlling parameters. The suction action permits Maxwell hybrid nanofluid molecules to occupy the sheet, resulting in the increment of the heat transfer rate, physically. When the thermal radiation parameter is increased, the heat transfer rate boosts due to the presence of thermal energy conversion. The augmentation of the nanoparticle volume fraction raises the Maxwell hybrid nanofluid viscosity, resulting in an upsurge in fluid velocity. A reduction value of the unsteadiness parameter that denotes the decelerating flow promotes the heat transfer rate significantly. Meanwhile, an increment in the Maxwell parameter value causes a decrement in the heat transfer rate due to the retarding force in the flow. Finally, the stability analysis guarantees the first solution's consistency, while the second solution is declared unstable.
| [1] |
MAXWELL, J. On the dynamical theory of gases. Philosophical Transactions of the Royal Society of London, 157, 49-88 (1867) |
| [2] |
HEYHAT, M. M. and KHABAZI, N. Non-isothermal flow of Maxwell fluids above fixed flat plates under the influence of a transverse magnetic field. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 225, 909-916 (2011) |
| [3] |
WANG, S. and TAN, W. Stability analysis of Soret-driven double-diffusive convection of Maxwell fluid in a porous medium. International Journal of Heat and Fluid Flow, 32, 88-94 (2011) |
| [4] |
NADEEM, S., HAQ, R. U., and KHAN, Z. H. Numerical study of MHD boundary layer flow of a Maxwell fluid past a stretching sheet in the presence of nanoparticles. Journal of the Taiwan Institute of Chemical Engineers, 45, 121-126 (2014) |
| [5] |
BINETTI, L., STANKIEWICZ, A., and ALWIS, L. Measurement of viscoelasticity of sodium alginate by fibre Bragg grating. Multidisciplinary Digital Publishing Institute Proceedings, 15, 33 (2019) |
| [6] |
PAWAR, S. S. and SUNNAPWAR, V. K. Experimental studies on heat transfer to Newtonian and non-Newtonian fluids in helical coils with laminar and turbulent flow. Experimental Thermal and Fluid Science, 44, 792-804 (2013) |
| [7] |
KUMAR, S., BHANJANA, G., SHARMA, A., SIDHU, M. C., and DILBAGHI, N. Synthesis, characterization and on-field evaluation of pesticide loaded sodium alginate nanoparticles. Carbohydrate Polymers, 101, 1061-1067 (2014) |
| [8] |
FAYAZ, M. A., BALAJI, K., GIRILAL, M., KALAICHELVAN, P. T., and VENKATESAN, R. Mycobased synthesis of silver nanoparticles and their incorporation into sodium alginate films for vegetable and fruit preservation. Journal of Agricultural and Food Chemistry, 57, 6246-6252 (2009) |
| [9] |
BAHIRAEI, M., GODINI, A., and SHAHSAVAR, A. Thermal and hydraulic characteristics of a mini channel heat exchanger operated with a non-Newtonian hybrid nanofluid. Journal of the Taiwan Institute of Chemical Engineers, 84, 149-161 (2018) |
| [10] |
AL-RASHED, A. A. A. A., SHAHSAVAR, A., ENTEZARI, S., MOGHIMI, M. A., ADIO, S. A., and NGUYEN, T. K. Numerical investigation of non-Newtonian water-CMC/CuO nanofluid flow in an offset strip-fin microchannel heat sink: thermal performance and thermodynamic considerations. Applied Thermal Engineering, 155, 247-258 (2019) |
| [11] |
NAGANTHRAN, K., NAZAR, R., and POP, I. Effects of heat generation/absorption in the Jeffrey fluid past a permeable stretching/shrinking disc. Journal of the Brazilian Society of Mechanical Sciences and Engineering, 41, 414 (2019) |
| [12] |
ESFE, M. H. On the evaluation of the dynamic viscosity of non-Newtonian oil based nanofluids: experimental investigation. predicting, and data assessment. Journal of Thermal Analysis and Calorimetry, 135, 97-109 (2019) |
| [13] |
NAGANTHRAN, K., NAZAR, R., and POP, I. Unsteady stagnation-point flow and heat transfer of a special third grade fluid past a permeable stretching/shrinking sheet. Scientific Reports, 6, 24632 (2016) |
| [14] |
EL-ZAHAR, E. R., RASHAD, A. M., SAAD, W., and SEDDEK, L. F. Magneto-hybrid nanofluids flow via mixed convection past a radiative circular cylinder. Scientific Reports, 10, 10494 (2020) |
| [15] |
RASHAD, A. M., CHAMKHA, A. J., ISMAEL, M. A., and SALAH, T. Magnetohydrodynamics natural convection in a triangular cavity filled with a Cu-Al2O3/water hybrid nanofluid with localized heating from below and internal heat generation. Journal of Heat Transfer, 140, 072502 (2018) |
| [16] |
GORLA, R. S. R., SIDDIQA, S. M., MANSOUR, M. A., RASHAD, A. M., and SALAH, T. Heat source/sink effects on natural convection of a hybrid nanofluid-filled porous cavity. Journal of Thermophysics and Heat Transfer, 31, 847-857 (2017) |
| [17] |
NAYAK, M. K., AKBAR, N. S., PANDEY, V. S., KHAN, Z. H., and TRIPATHI, D. 3D free convective MHD flow of nanofluid over permeable linear stretching sheet with thermal radiation. Powder Technology, 315, 205-215 (2017) |
| [18] |
ZAINAL, N. A., NAZAR, R., NAGANTHRAN, K., and POP, I. MHD flow and heat transfer of hybrid nanofluid over a permeable moving surface in the presence of thermal radiation. International Journal of Numerical Methods for Heat and Fluid Flow, 31, 858-879 (2021) |
| [19] |
CESS, R. D. The interaction of thermal radiation with free convection heat transfer. International Journal of Heat and Mass Transfer, 9, 1269-1277 (1966) |
| [20] |
ARPACI, V. S. Effect of thermal radiation on the laminar free convection from a heated vertical plate. International Journal of Heat and Mass Transfer, 11, 871-881 (1968) |
| [21] |
AGBAJE, T. M., MONDAL, S., MOTSA, S. S., and SIBANDA, P. A numerical study of unsteady non-Newtonian Powell-Eyring nanofluid flow over a shrinking sheet with heat generation and thermal radiation. Alexandria Engineering Journal, 56, 81-91 (2017) |
| [22] |
TAKABI, B. and SALEHI, S. Augmentation of the heat transfer performance of a sinusoidal corrugated enclosure by employing hybrid nanofluid. Advances in Mechanical Engineering, 6, 147059 (2014) |
| [23] |
GHALAMBAZ, M., ROŞCA, N. C., ROŞCA, A. V., and POP, I. Mixed convection and stability analysis of stagnation-point boundary layer flow and heat transfer of hybrid nanofluids over a vertical plate. International Journal of Numerical Methods for Heat and Fluid Flow, 30, 3737-3754 (2020) |
| [24] |
ANUAR, N. S. and BACHOK, N. Double solutions and stability analysis of micropolar hybrid nanofluid with thermal radiation impact on unsteady stagnation point flow. Mathematics, 9, 276 (2021) |
| [25] |
KHASHI'IE, N. S., ARIFIN, N. M., POP, I., NAZAR, R., and HAFIDZUDDIN, E. H. A new similarity solution with stability analysis for the three-dimensional boundary layer of hybrid nanofluids. International Journal of Numerical Methods for Heat and Fluid Flow, 31, 809-828 (2021) |
| [26] |
WAINI, I., ISHAK, A., and POP, I. Agrawal flow of a hybrid nanofluid over a shrinking disk. Case Studies in Thermal Engineering, 25, 100950 (2021) |
| [27] |
KOPLIK, J. and BANAVAR, J. R. The no-slip condition for a mixture of two liquids. Physical Review Letters, 80, 5125-5128 (1998) |
| [28] |
MAY, S. E. and MAHER, J. V. Capillary-wave relaxation for a meniscus between miscible liquids. Physical Review Letters, 67, 2013-2016 (1991) |
| [29] |
MADHU, M., KISHAN, N., and CHAMKHA, A. J. Unsteady flow of a Maxwell nanofluid over a stretching surface in the presence of magnetohydrodynamic and thermal radiation effects. Propulsion and Power Research, 6, 31-40 (2017) |
| [30] |
OZTOP, H. F. and ABU-NADA, E. Numerical study of natural convection in partially heated rectangular enclosures filled with nanofluids. International Journal of Numerical Methods for Heat and Fluid Flow, 29, 1326-1336 (2008) |
| [31] |
ROSSELAND, S. Theoretical Astrophysics, Oxford University Press, Oxford (1936)
|
| [32] |
WAINI, I., ISHAK, A., and POP, I. Flow and heat transfer of a hybrid nanofluid past a permeable moving surface. Chinese Journal of Physics, 66, 606-619 (2020) |
| [33] |
WAINI, I., ISHAK, A., and POP, I. Hybrid nanofluid flow on a shrinking cylinder with prescribed surface heat flux. International Journal of Numerical Methods for Heat and Fluid Flow, 31, 1987-2004 (2020) |
| [34] |
KHASHI'IE, N. S., ARIFIN, N. M., POP, I., and NAZAR, R. Melting heat transfer in hybrid nanofluid flow along a moving surface. Journal of Thermal Analysis and Calorimetry (2020) https://doi.org/10.1007/s10973-020-10238-4 |
| [35] |
MERKIN, J. H. Natural convective boundary-layer flow in a heat-generating porous medium with a prescribed wall heat flux. Zeitschrift für Angewandte Mathematik und Physik, 60, 543-564 (2009) |
| [36] |
MERRILL, K., BEAUCHESNE, M., PREVITE, J., PAULLET, J., and WEIDMAN, P. Final steady flow near a stagnation point on a vertical surface in a porous medium. International Journal of Heat and Mass Transfer, 49, 4681-4686 (2006) |
| [37] |
ZAINAL, N. A., NAZAR, R., NAGANTHRAN, K., and POP, I. Unsteady three-dimensional MHD non-axisymmetric Homann stagnation point flow of a hybrid nanofluid with stability analysis. Mathematics, 8, 784 (2020) |
| [38] |
ZAINAL, N. A., NAZAR, R., NAGANTHRAN, K., and POP, I. Unsteady EMHD stagnation point flow over a stretching/shrinking sheet in a hybrid Al2O3-Cu/H2O nanofluid. International Communications in Heat Mass Transfer, 123, 105205 (2021) |
| [39] |
WEIDMAN, P. D., KUBITSCHEK, D. G., and DAVIS, A. M. J. The effect of transpiration on self-similar boundary layer flow over moving surfaces. International Journal of Engineering Science, 44, 730-737 (2006) |
| [40] |
HARRIS, S. D., INGHAM, D. B., and POP, I. Mixed convection boundary-layer flow near the stagnation point on a vertical surface in a porous medium: Brinkman model with slip. Transport in Porous Media, 77, 267-285 (2009) |
| [41] |
SHAMPINE, L. F., GLADWELL, I., and THOMPSON, S. Solving ODEs with MATLAB, Cambridge University Press, Cambridge (2003)
|
| [42] |
SHARIDAN, S., MAHMOOD, T., and POP, I. Similarity solutions for the unsteady boundary layer flow and heat transfer due to a stretching sheet. Applied Mechanics and Engineering, 11, 647-654 (2006) |
| [43] |
CHAMKHA, A., ALY, A., and MANSOUR, M. Similarity solution for unsteady heat and mass transfer from a stretching surface embedded in a porous medium with suction/injection and chemical reaction effects. Chemical Engineering Communications, 197, 846-858 (2010) |
| [44] |
USMAN, M., HAMID, M., ZUBAIR, T., UL-HAQ, R., and WANG, W. Cu-Al2O3/water hybrid nanofluid through a permeable surface in the presence of nonlinear radiation and variable thermal conductivity via LSM. International Journal of Heat and Mass Transfer, 126, 1347-1356 (2018) |

 2021, Vol. 42
2021, Vol. 42