Shanghai University
Article Information
- XIE-SHENG GE, KUI ZOU. 2014.
- Open-plus-closed-loop control for chaotic motion of 3D rigid pendulum
- Appl. Math. Mech. -Engl. Ed., 35(4): 403-412
- http://dx.doi.org/10.1007/s10483-014-18800-8
Article History
- Received 2013-02-25;
- in final form 2013-06-03
2. Department of Electrical and Computer Engineering, Faculty of Engineering, King Abdulaziz University, Jeddah 21589, Saudi Arabia
It is a kind of generalized rigid 3D pendulum that consists of a rigid body supported by a fixed and frictionless pivot with three rotational degrees,acted by a constant gravitational force. Symmetry assumptions are shown to lead to the spherical 2D pendulum if the angular velocity around the axis of symmetry is zero,and the 3D rigid pendulum is referred as a Lagrange top if the angular velocity around the axis of symmetry is a non-zero constant. Many literatures about axially symmetry 3D rigid pendulum have been published.
In 2004,Shen et al.[1] proposed the reduced attitude model of 3D rigid with Euler’s angles formulation. Chaturvedi et al.[2] studied the Poincarémapping with the reduced attitude model. Chang and Ge[3] studied the chaotic motion of the 3D rigid pendulum in the inertial coordinate frame with the Poincaré surface of section method. The chaoticmotion of the 3D rigid pendulum makes the controller’s design more difficult and the research more significant. The stabilization of the 3D rigid pendulum has been studied in recent years. Chaturvedi et al.[4] designed the attitude controllers for the 3D rigid pendulum at inverted equilibrium position with angular velocity feedback and attitude feedback. Santillo et al.[5] realized the attitude stabilization for the 3D rigid pendulum at hanging equilibrium position with angular velocity feedback.
In 1995,Jackson and Grosu[6] and Jackson[7] proposed the open-plus-closed-loop (OPCL) control method for the complex dynamic system,and then Chen and Liu’s group[8, 9, 10, 11] researched the OPCL approach and its applications for chaotic motion of nonlinear oscillators. To avoid the singular problem and complex trigonometric function of Lagrange’s equation,the quaternion matrix equation Euler’s dynamic equation are used to describe the 3D rigid pendulum,and then we analyze the dynamic characteristic with the Poincaré section.
The present paper continues our research on the control of an asymmetric 3D rigid pendulum. For complex motion of the 3D rigid pendulum,an OPCL controller,which contains two parts: the open-loop part to construct an ideal trajectory and the closed-loop part to calm the 3D rigid pendulum down,is designed. 2 Mathematical model of 3D rigid pendulum
The 3D rigid pendulum rotates around a fixed and frictionless pivot O with three degrees. An inertial coordinate frame O-XYZ has its origin at the pivot O,and the first two coordinate axes X and Y lie in the horizontal plane along the inertia principal axis direction while the third coordinate axis Z is vertical in the direction of gravity. The origin of the body fixed coordinate frame O-X′Y ′Z′ is also located at the pivot. In this frame,the inertia matrix J is constant. A schematic of a 3D rigid pendulum is shown in Fig. 1. Consider Euler’s dynamic equation of the 3D rigid pendulum[1]
 |
| Fig. 1 Schematic of 3D rigid pendulum |
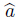 b,where
b,where 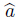 is the skew-symmetric matrix as follows:
The parameter R in (1) stands for the direction cosine matrix which is described by quaternion as follows:
The attitude kinematics equations described by quaternion are
where the quaternion has to satisfy the following holonomic equation:
The angular velocities described by the quaternion from (2) can be obtained as
The nonholonomic constraint (speed) equation is
Form (4),we can obtain
Taking the second derivative of (3),we have
Substituting (4) and (6) into (1) and combining with (7),a second-order ordinary differential equation which consists of quaternion and whose derivative function will be produced,can be expressed as follows:
where
is the skew-symmetric matrix as follows:
The parameter R in (1) stands for the direction cosine matrix which is described by quaternion as follows:
The attitude kinematics equations described by quaternion are
where the quaternion has to satisfy the following holonomic equation:
The angular velocities described by the quaternion from (2) can be obtained as
The nonholonomic constraint (speed) equation is
Form (4),we can obtain
Taking the second derivative of (3),we have
Substituting (4) and (6) into (1) and combining with (7),a second-order ordinary differential equation which consists of quaternion and whose derivative function will be produced,can be expressed as follows:
where 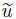 = [uT 0]T,and
The determinant of M(q) is 16J1J2J3 > 0. The components of F(q,
= [uT 0]T,and
The determinant of M(q) is 16J1J2J3 > 0. The components of F(q,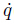 ) are as follows:
where
) are as follows:
where 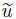 = [uT 0]T,and
3 Chaotic motion of 3D rigid pendulum
= [uT 0]T,and
3 Chaotic motion of 3D rigid pendulum
In this section,we present the chaotic motion of an uncontrolled 3D rigid pendulum. It is well known that chaotic motion is very sensitive to the initial conditions. The chaotic motion will be observed if we choose proper initial values with q(0) and 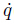 (0). Consider an uncontrolled 3D rigid pendulum,the parameters in (8) are J = diag(40 45 50) kg · m2,g = 9.8 m/s2,l = 0.5 m,m = 140 kg,and λ = -1. We choose q(0) = (0 0 0 1)T and
(0). Consider an uncontrolled 3D rigid pendulum,the parameters in (8) are J = diag(40 45 50) kg · m2,g = 9.8 m/s2,l = 0.5 m,m = 140 kg,and λ = -1. We choose q(0) = (0 0 0 1)T and 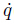 (0) = (0.1 0.1 0 0)T. We observe the vector ω in the inertial coordinate frame. Figure 2 shows the angular velocity phase diagram of the 3D rigid pendulum. Figures 3-5 show us the time history of the angular velocities.
(0) = (0.1 0.1 0 0)T. We observe the vector ω in the inertial coordinate frame. Figure 2 shows the angular velocity phase diagram of the 3D rigid pendulum. Figures 3-5 show us the time history of the angular velocities.
 |
| Fig. 2 Phase diagram of angular velocity ω |
 |
| Fig. 3 Angular velocity ωx with time |
 |
| Fig. 4 Angular velocity ωy with time |
 |
| Fig. 5 Angular velocity ωz with time |
Figure 6 is the Poincaré section of the angular velocities,and we can conclude that the 3D pendulum appears the chaotic motion. At first,the pendulum is located in the inverted equilibrium position,then it takes on chaotic motion if the initial value of 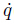 is a nonzero vector,and the quaternion changes irregularly with time.
is a nonzero vector,and the quaternion changes irregularly with time.
 |
| Fig. 6 Poincaré section of angular velocity ω(ωz=0) |
Consider the chaotic motion of the 3D rigid pendulum,an OPCL controller is designed in this section. From (8),we can get
By assuming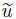 = M-1
= M-1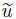 and
and 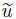 = (υ1 υ2 υ3 υ4)T,we have
Equations (10)-(12) can be written in the vector form as
where q = [q1 q2 q3]T,f = [f1 f2 f3]T,and υ = [υ1 υ2 υ3]T.
= (υ1 υ2 υ3 υ4)T,we have
Equations (10)-(12) can be written in the vector form as
where q = [q1 q2 q3]T,f = [f1 f2 f3]T,and υ = [υ1 υ2 υ3]T.
Define the error as e =q-p,where p stands for the control objective function. Introduce the OPCL law[12]
where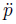 -h(p,
-h(p,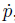 ,t) is the open loop part,the rest of them are the closed loop parts,A and B are the coefficient matrices of the controller. Substituting (15) into (14),we can get the error function of the system
Select the Lyapunov function as follows:
Its derivative function is
where I is an unit matrix. If we make B = -I and A < 0,then we can get
,t) is the open loop part,the rest of them are the closed loop parts,A and B are the coefficient matrices of the controller. Substituting (15) into (14),we can get the error function of the system
Select the Lyapunov function as follows:
Its derivative function is
where I is an unit matrix. If we make B = -I and A < 0,then we can get 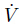 (e,
(e,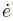 ) =
) = 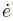 TA
TA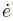 < 0. According to the Lyapunov stable theory,q1,q2,and q3 are globally asymptotically stable. From
< 0. According to the Lyapunov stable theory,q1,q2,and q3 are globally asymptotically stable. From 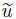 = M
= M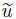 ,we can get
5 Simulation results and analysis
5.1 Inverted equilibrium
,we can get
5 Simulation results and analysis
5.1 Inverted equilibrium
Considering the chaotic characteristics of the 3D rigid pendulum,we simulate the inverted equilibrium of the 3D rigid pendulum in this section. When the 3D rigid pendulum reaches the inverted equilibrium,and λ = -1,the reduced attitude Γ = [0 0 -1]T. Then,we have 2(q42 + q32) -1 = 1,i.e.,q42 + q32= 1,q1 = 0,and q2 = 0. From (19),it can be seen that q4 ≠ 0. Therefore,the valuesq1 = 0,q2 = 0,q3 = 0,and q42 = 1 are introduced as the final equilibrium state. For the inverted equilibrium of the 3D rigid pendulum,the parameters in (8) are J = diag(40 45 50) kg · m2,g = 9.8 m/s2,l = 0.5 m,and m = 140 kg. We choose the same initial conditions q(0) = (0 0 0 1)T and 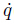 (0) = (0.1 0.1 0 0)T.
(0) = (0.1 0.1 0 0)T.
The initial values of quaternion and its derivative have to satisfy the constraint from (5). For the OPCL control law in (15),the objective function as p = (0 0 0)T is selected,and A = B = -I is used as the coefficient matrix. When the controller is opened at the 11st second,the evolution of quaternion for the 3D rigid pendulum at inverted equilibrium is shown in Fig. 7. From Figs. 8 and 9,it can be concluded that the 3D rigid pendulum finally reaches the inverted equilibrium. Figure 10 shows us the input control moment of 3D rigid pendulum for the inverted equilibrium.
 |
| Fig. 7 Evolution of quaternion of 3D rigid pendulum at inverted equilibrium |
 |
| Fig. 8 Evolution of angular velocity of 3D rigid pendulum at inverted equilibrium |
 |
| Fig. 9 Evolution of reduced attitude of 3D rigid pendulum at inverted equilibrium |
 |
| Fig. 10 Input control moment of 3D rigid pendulum for inverted equilibrium |
Considering the same pendulum,we simulate the hanging equilibrium of the 3D rigid pendulum in this section. When the 3D rigid pendulum reaches the hanging equilibrium,and λ = 1,the reduced attitude Γ = [0 0 1]T. Then,we have 2(q42+q32)-1 = 1,i.e.,q42+q32 = 1,q1 = 0,and q2 = 0. For the hanging equilibrium of the 3D rigid pendulum,we choose the initial conditions q(0) = (0 0.6 0.8 0)T. and 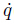 (0) = (0.1 0 0 0.1)T. We select the objective function as p = (0 0 0)T and A = B = -I as the coefficient matrix. When the controller is opened at the 8th second,Fig. 11 shows the evolution of quaternion of the 3D rigid pendulum at the hanging equilibrium. From Figs. 12 and 13,we can conclude that the 3D rigid pendulum finally reaches the hanging equilibrium. Figure 14 shows us the input control moment of the 3D rigid pendulum for the hanging equilibrium.
(0) = (0.1 0 0 0.1)T. We select the objective function as p = (0 0 0)T and A = B = -I as the coefficient matrix. When the controller is opened at the 8th second,Fig. 11 shows the evolution of quaternion of the 3D rigid pendulum at the hanging equilibrium. From Figs. 12 and 13,we can conclude that the 3D rigid pendulum finally reaches the hanging equilibrium. Figure 14 shows us the input control moment of the 3D rigid pendulum for the hanging equilibrium.
 |
| Fig. 11 Evolution of quaternion of 3D rigid pendulum at hanging equilibrium |
 |
| Fig. 12 Evolution of angular velocity of 3D rigid pendulum at hanging equilibrium |
 |
| Fig. 13 Evolution of reduced attitude of 3D rigid pendulum at hanging equilibrium |
 |
| Fig. 14 Input control moment of 3D rigid pendulum for hanging equilibrium |
In order to avoid the singular phenomenon of Euler’s angular velocity equation,the quaternion kinematic equation is used to describe the 3D rigid pendulum in this paper. We design an OPCL controller for chaotic motion of the 3D rigid pendulum at the inverted equilibrium position. The OPCL controller contains two parts: the open-loop part to construct an ideal trajectory and the closed-loop part to calm the 3D rigid pendulum down. Simulation results show that this control law can fulfill the attitude control for the 3D rigid pendulum at the inverted and hanging equilibrium positions.
| [1] | Shen, J., Sanyal, A. K., Chaturvedi, N. A., Bernstein, D., and McClamroch, N. H. Dynamics andcontrol of a 3D pendulum. Proceeding of 43rd IEEE Conference on Decision and Control, IEEEPress, Bahamas, 323–328 (2004) |
| [2] | Chaturvedi, N. A., Lee, T., Leok, M., and McClamroch, N. H. Nonlinear dynamic of the 3Dpendulum. Journal of Nonlinear Science, 21(1), 3–32 (2011) |
| [3] | Chang, J. and Ge, X. S. Chaotic attitude motion of the 3D rigid pendulum. Proceeding of 3rdInternational Conference on Advanced Computer Control, IEEE Press, Harbin, 470–472 (2011) |
| [4] | Chaturvedi, N. A., Bacconi, F., Sanyal, A. K., Bernstein, D., and McClamroch, N. H. Stabilizationof a 3D rigid pendulum. Proceeding of American Control Conference, IEEE Press, Ann Arbor,3030–3035 (2005) |
| [5] | Santillo, M. A., Chaturvedi, N. A., Bacconi, F., McClamroch, N. H., and Bernstein, D. Exper-iments on stabilization of the hanging equilibrium of a 3D asymmetric rigid pendulum. IEEEConference on Control Applications, IEEE Press, Toronto, 308–313 (2005) |
| [6] | Jackson, E. A. and Grosu, I. An open-plus-close-loop (OPCL) control of complex dynamic systems.Nonlinear Phenomena, 85(1), 1–9 (1995) |
| [7] | Jackson, E. A. The OPCL control for entrainment, model-resonance and migration actions onmulti-attractor systems. Chaos, 7(4), 550–559 (1997) |
| [8] | Chen, L. Q. and Liu, Y. Z. An open-plus-closed-loop control for chaotic motion of nonlinearoscillators (in Chinese). Journal of Applied Science, 17(4), 445–449 (1999) |
| [9] | Chen, L. Q. An open-plus-closed-loop control for discrete chaos and hyperchaos. Physics LettersA, 281(5-6), 327–333 (2001) |
| [10] | Chen, L. Q. and Liu, Y. Z. An open-plus-closed-loop approach to synchronization of chaotic andhyperchaotic maps. International Journal of Bifurcation and Chaos, 12(5), 1219–1225 (2002) |
| [11] | Chen, L. Q. and Liu, Y. Z. The parametric open-plus-closed-loop control of chaotic maps and itsrobustness. Chaos, Solitons and Factals, 21(1), 113–118 (2004) |
| [12] | Han, Q. K., Zhao, X. Y., and Wen, B. C. Synchronization motion of a two-link mechanism with animproved OPCL method. Applied Mathematics and Mechanics (English Edition), 29(12), 1561–1568 (2008) DOI 10.1007/s10483-008-1204-z |
 2014, Vol. 35
2014, Vol. 35























