Shanghai University
Article Information
- QIN-HUANG DONG, LI CHEN. 2014.
- Impact dynamics analysis of free-floating space manipulator capturing satellite on orbit and robust adaptive compound control algorithm design for suppressing motion
- Appl. Math. Mech. -Engl. Ed., 35(4): 413-422
- http://dx.doi.org/10.1007/s10483-014-1801-7
Article History
- Received 2013-03-27;
- in final form 2013-09-16
B0,free-floating base;
Bi,link of manipulator (i = 1,2);
B3,target satellite;
O0,centre of free-floating base;
Oi,joint centre (i = 1,2);
O-XY,inertial coordinate;
Oi-XiYi,local coordinate of Bi (i = 0,1,2);
Cm,centre of target satellite;
P,end-effector of space manipulator;
P′,handle on satellite surface which impact with end-effector of manipulator;
l0,distance between l0 and l1;
li,length of link Bi(i = 1,2);
l3,distance between Cm,and P′;
mi,mass of Bi (i = 0,1,2,3);
Ji,center inertial momentum ofBi(i=0,1,2,3). 1 Introduction
As the astronautic technology developing,the space manipulator will be employed to manage more assignments for helping the astronaut in the aerospace. It is attracting the attention of researchers[1, 2, 3, 4, 5]. The space manipulator was employed in the space station firstly,then equipped in the space shuttle. Now,the free-floating space manipulator is becoming a new research area[6]. The free-floating space manipulator can be employed in a wider work space on orbit to finish the repair,retrieve,and fuel refill of satellite services. In finishing the above services,the endeffector of space manipulator will impact with the satellite inevitably,the impact will cause the unstable motion or even cause damage of space manipulator,the dynamics and control of space manipulator capturing the satellite are more complex than the non-capture operation[7, 8].
In this paper,the impact dynamics and control of free-floating space manipulator capturing a satellite are analyzed. Firstly,based on the kinematics analysis,the dynamics equation of free-floating space manipulator system is derived by the second Lagrangian equation,and then according to the momentum conservation principle,the impact dynamics and effect of the capture process are analyzed by the momentum impulse. Considering the unstable motion of space manipulator which is caused by the impact of satellite,a robust adaptive compound control algorithm is designed to suppress the unstable motion of the space manipulator,it can eliminate the effect of uncertain and unknown parameters of space manipulator and satellite for the control,and the stability of the control algorithm is proved by the Lyapunov theorem. Finally,the simulation is proposed to reveal the impact effect and verify the validity of the control algorithm. 2 Kinematics analysis
The process of planar free-floating space manipulator capturing a target satellite on orbit is shown in Fig. 1. The capture process can be divided into three stages: the pre-impact stage between the manipulator end-effector and the target satellite handle,the impact stage,and the post-impact stage in which the space manipulator and satellite get combination.
 |
| Fig. 1 Free-floating space manipulator system and target satellite |
The kinematic equation of the space manipulator which represents the relationship between the velocity of end-effector P and the generalized velocity is
where VP =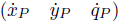 T ∈ R3×1 is the velocity of end-effector P in the inertial frame,q = (x0 y0 α θ1 θ2)T ∈ R5×1 is the generalized coordinates vector of space manipulator which represents the free-floating base position and attitude,and the manipulator joint angle,and J ∈ R3×5 is the corresponding Jacobian matrix.
T ∈ R3×1 is the velocity of end-effector P in the inertial frame,q = (x0 y0 α θ1 θ2)T ∈ R5×1 is the generalized coordinates vector of space manipulator which represents the free-floating base position and attitude,and the manipulator joint angle,and J ∈ R3×5 is the corresponding Jacobian matrix.
Similarly,the kinematic equation of the satellite can be expressed as follows:
where VP′ =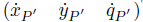 T ∈ R3×1 is the velocity of the satellite handle P′ in the inertial frame,φ = (xcm ycm β)T ∈ R3×1 is the generalized coordinate vector of satellite which represents the position and attitude,and JP′ ∈ R3×3 is the corresponding Jacobian matrix.
3 Dynamics analysis
T ∈ R3×1 is the velocity of the satellite handle P′ in the inertial frame,φ = (xcm ycm β)T ∈ R3×1 is the generalized coordinate vector of satellite which represents the position and attitude,and JP′ ∈ R3×3 is the corresponding Jacobian matrix.
3 Dynamics analysis3.1 Dynamic equation of free-floating space manipulator of pre-impact stage
The free-floating base position of space manipulator is uncontrolled for saving the jet fuel as shown in Fig. 1,the dynamic equation can be derived by the second Lagrangian equation as follows:
where D ∈ L5×5 is the symmetric positive definite inertial matrix,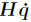 ∈ R5×1 is the vector of the Coriolis and centrifugal force,τ = (0 0 τ0 τ1 τ2)T ∈ R5×1 is the control input,the base position is uncontrolled for saving the jet fuel,and FP = (FPx FPy MP )T ∈ R3×1 is the external force which acts on the end-effector.
3.2 Impact dynamics and effect of impact stage
∈ R5×1 is the vector of the Coriolis and centrifugal force,τ = (0 0 τ0 τ1 τ2)T ∈ R5×1 is the control input,the base position is uncontrolled for saving the jet fuel,and FP = (FPx FPy MP )T ∈ R3×1 is the external force which acts on the end-effector.
3.2 Impact dynamics and effect of impact stageAssume the satellite is free motion on orbit which will be captured by the space manipulator, and the dynamic equation of satellite can be expressed as
where Dt = diag(m3,m3,J3) ∈ R3×3 is the inertial matrix,Ct ∈ R3×1 is the vector of the Coriolis and centrifugal force,and FP′ is the impact force which acts on the satellite handle during the impact stage.The impact between the manipulator end-effector and the target satellite is inevitably during the capture process,where FP and FFP′ are the interact forces. According to the impulse principle,it is known that the fact of the impact is the momentum transfer between the space manipulator and satellite. The impact affects the motion of space manipulator. By combining (3) and (4),and eliminating the interact force as follows,we can get
Assume the duration of the impact stage is △t. According to the momentum impulse,the integral of (5) for the duration △t can be expressed as follows:
where t0 is the moment before impact. Since the duration of the impact stage is very short and the interact force is very large,the generalized coordinates of the space manipulator remain unchanged during the impact stage although the rate may change. Besides,there is not any control input during the impact stage to avoid joint damage by impact impulse,i.e.,τ = 0. It can be expressed in a mathematical form as Thus,the integral can be further written as follows: where the subscripts i and f of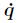 and
and 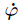 represent before and after the impact,respectively. Since D,Dt,J,and JP′ depend on the generalized coordinates only,they remain the same during the impact stage. D,Dt,J,and JP′ are the values of D,Dt,J,and JP′ at moment t0. We know the left of (7) is O(1),the integrand of right is O(1),however the integration time △t = O(ε),the right of (7) is O(ε). (7) can be written as follows:
represent before and after the impact,respectively. Since D,Dt,J,and JP′ depend on the generalized coordinates only,they remain the same during the impact stage. D,Dt,J,and JP′ are the values of D,Dt,J,and JP′ at moment t0. We know the left of (7) is O(1),the integrand of right is O(1),however the integration time △t = O(ε),the right of (7) is O(ε). (7) can be written as follows:
The derivation of (8) based on the momentum conservation can be used from perfect elastic impact to plastic impact situation. On the assumption that it is perfect plastic impact between the end-effector P and the satellite handle P′ during the capture process,i.e.,the manipulator captures the satellite successfully. Since the impact point plastic deformation is very small relative to the structure dimension,the end-effector P of space manipulator and handle P′ of satellite have the same velocity after impact. Thus,
By combining (8) and (9),at the moment t0 + △t,the generalized velocity of space manipulator after impact can be expressed as
where(10) represents the impact effect for the space manipulator motion during the impact stage,it will cause the unstable motion of space manipulator after capture the satellite. Therefore,the control for suppressing motion is necessary. 3.3 Impact dynamic equation of combination system of post-impact stage
After the space manipulator capturing the satellite successfully,they will become the combination system,the dynamic equation of combination system contains space manipulator subsystem and satellite subsystem. Thus,
The derivative of (11) can be rewritten as follows:
The interact force between the space manipulator and satellite becomes the internal force for the combination system during the post-impact stage,assuming there is not any other external force acting on the combination system of the capture process. Thus,(5) can be described as the dynamic equation of the combination system of the post-impact stage. By substituting (11) and (12) into (5) and with linear treating,we get
where(13) is the dynamic equation of combination system of the post-impact stage. A relationship exists between Hz ∈ R5×5 and a random vector z ∈ R5×1[9],
4 Robust adaptive compound control algorithm design of space manipulator for suppressing unstable motion due to impact effectThe impact effect will cause the unstable motion of the combination system,such as the base movement,rotation,and joint irregular motion that will affect the normal operation of the solar panels and antenna,and damage the joint hinge due to over rotate. Therefore,in order to ensure the combination system normal operation,the applying of control for suppressing motion is necessary. Based on (13),a robust adaptive compound control algorithm of space manipulator is designed to suppress the unstable motion of the combination system,and it can be used to under the inertial parameters unknown or uncertain and the base position being uncontrolled.
Define the control output of the combination system as qr = (α θ1 θ2)T ∈ R3×1,the virtual augmented output is q = (qbT qrT)T ∈ R5×1,and qb = (x0 y0)T ∈ R2×1 is the position of the free-floating base. Assume the position qb,the velocity 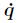 b,and the acceleration
b,and the acceleration  of the free-floating base can be measured or calculated,and the error between the desired augmented output qd = (qbT qrdT)T ∈ R5×1 and virtual augmented output is
of the free-floating base can be measured or calculated,and the error between the desired augmented output qd = (qbT qrdT)T ∈ R5×1 and virtual augmented output is
Define the augmented error of system as
where λ> 0 is the constant,and s1 =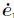 r + λer. Define the reference output joint velocity
r + λer. Define the reference output joint velocity 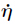 and reference output joint acceleration
and reference output joint acceleration 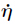 as
Therefore,according to (16) and (17),we can get
This is the combination system error equation,and τr =(τ0 τ1 τ2)T.
as
Therefore,according to (16) and (17),we can get
This is the combination system error equation,and τr =(τ0 τ1 τ2)T.
Based on (19),the robust adaptive compound control algorithm is proposed as follows:
where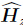 z and
z and 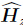 z are the estimation of Dz and Hz,the vector δ∈ R2×1 ensures the upper two rows of the right of (19) to be zero,K1 ∈ R3×3 is a random symmetric positive definite matrix,and Q = diag( Q1,Q2,Q3)∈ R3×3 is a undetermined matrix.
z are the estimation of Dz and Hz,the vector δ∈ R2×1 ensures the upper two rows of the right of (19) to be zero,K1 ∈ R3×3 is a random symmetric positive definite matrix,and Q = diag( Q1,Q2,Q3)∈ R3×3 is a undetermined matrix.
Substituting (20) into (19),we can get
where WΦ = (Dsub>z-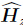 z)
z)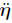 + (Hz −Hcz)
+ (Hz −Hcz)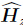
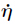 ,W is the function of q,
,W is the function of q,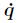 ,
,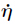 ,and
,and 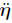 that does not contain undetermined parameters,Φ = ξ-
that does not contain undetermined parameters,Φ = ξ-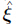 is the vector of estimation error of uncertain or unknown parameters,and ξ and
is the vector of estimation error of uncertain or unknown parameters,and ξ and 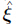 are the true value and estimated value of the parameters,respectively.
are the true value and estimated value of the parameters,respectively.
The inertial parameters of space manipulator are always uncertain,and they vary within a range as a result of fuel consuming. The inertial parameters of the target satellite are always unknown as an external body of space manipulator. Therefore,WΦ can be decomposed as follows:
where ΦR = ξ<>R-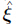 R represents the vector of estimation error of uncertain inertial parameters of space manipulator,and ΦS = ξS-
R represents the vector of estimation error of uncertain inertial parameters of space manipulator,and ΦS = ξS-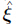 S represents the vector of estimate error of unknown inertial parameters of target satellite.
S represents the vector of estimate error of unknown inertial parameters of target satellite.
Assume that the inertial vector of space manipulator varies in a definite range as follows:
The above control algorithm does not need to self-adjust the uncertain inertial parameters,and will keep robust if the estimated parameters do not exceed the definite range,which will increase the computational efficiency of the control system. The following theorem exists for the control algorithm.
Lemma 1 If under the appropriative determination of the undetermined matrix Q,the following adaptive law equation (24) is used to adjust the unknown inertial parameters for the control algorithm,the control algorithm will guarantee  = 0.
= 0.
Remark 1 Assuming s = 0 and Φ= 0 represent no interference motion. (21) and (24) are interference motion equations,and the Lyapunov function is defined as follows:
By combining (14),(21),and (24),we can get
where K2 = diag(I2×2,K1). It is obviously that-γsTK2s 6 0,and the first term of (26) can be written as where n is the number of elements of the matrix ΦR,ΦRj represents the corresponding element of ΦR,WR3j ,WR4j ,and WR5j represent the elements of the matrix WR,and s11,s12,and s13 represent the elements of the vector s1. If the undetermined matrix Q is determined as where μi is the positive constant,then (27) satisfies the following relationship:By substituting (29) into (26),we can get
By analyzing (30),we known that  is negative definite,and
is negative definite,and  = 0 only exists when s = 0. Therefore,
= 0 only exists when s = 0. Therefore, = 0 is satisfied.
5 Simulations
= 0 is satisfied.
5 Simulations
To reveal the impact effect during the capture operation and verify the validity of the control algorithm,a simulation of free-floating space manipulator capturing a satellite shown in Fig. 1 is carried out. The parameters are taken as follows:
The uncertain and unknown parameters are taken as
The initial moment of the simulation is 0 s,and the duration of the simulation is 10 s. At 0 s,it is assumed that the space manipulator is adjusted to a desired position and configuration,and waited for capturing the satellite. At t0 = 1 s,the free motion satellite (velocity:  = −0.3 m/s,
= −0.3 m/s, = 0.3 m/s,
= 0.3 m/s, = 0.1 rad/s) is flying toward the end-effector of space manipulator,and then satellite impacts with end-hand,the duration of impact stage is △t (assume △t = 0.2 s here). The impact effect will cause the unstable motion of combination system. Therefore,it is necessary to employ the active control for suppressing motion of the combination system.
= 0.1 rad/s) is flying toward the end-effector of space manipulator,and then satellite impacts with end-hand,the duration of impact stage is △t (assume △t = 0.2 s here). The impact effect will cause the unstable motion of combination system. Therefore,it is necessary to employ the active control for suppressing motion of the combination system.
The parameters of control algorithm are taken as
The estimations of uncertain inertial parameters of the space manipulator are taken as The estimation of unknown parameters of the target satellite are taken as Two different simulations are carried out for comparing.Simulation 1 There is not any control algorithm used for suppressing the unstable motion of combination system after the impact between the space manipulator and satellite,the space manipulator is under uncontrolled state. Figure 2 shows the time history of the base attitude and joint angle under uncontrolled after impact. Figure 3 shows the time history of base rotation velocity and joint angle velocity under uncontrolled after impact. The above simulation results reveal the impact effect for the motion during the capture operation.
 |
| Fig. 2 Time history of base attitude and joint angle under uncontrolled after impact |
 |
| Fig. 3 Time history of base rotation velocity and joint angle velocity under uncontrolled after impact |
Simulation 2 A robust adaptive compound control algorithm is used for suppressing the unstable motion of combination system after the impact between the space manipulator and satellite,the space manipulator is under active controlled state. Figure 4 shows the time history of base attitude and joint angle under active controlled after impact. Figure 5 shows the time history of the base rotation velocity and joint angle velocity under active controlled after impact. By comparing the results of Simulation 1 and Simulation 2,the validity of the active control for suppressing motion is obvious.
 |
| Fig. 4 Time history of base attitude and joint angle under active controlled after impact |
 |
| Fig. 5 Time history of base rotation velocity and joint angle velocity under active controlled after impact |
In this paper,the dynamics of free-floating space manipulator capturing a target satellite on orbit are analyzed,and the active control for suppressing the unstable motion of combination system during the capture operation is proposed. By the analyzing,the following conclusions can be drawn.
Firstly,by the dynamics analysis and simulations,we can find that the impact effect for the stability of space manipulator system is obvious. Therefore,the active control for suppressing the unstable motion of space manipulator during capturing the satellite is necessary.
Secondly,some difficulties need to be considered for the active control in advance: the uncertain or unknown parameters effect for the control algorithm,the uncontrolled of freefloating base during the active control applied. In this paper,the robust adaptive compound control can be applied under the above situation.
Finally,the process of space manipulator capturing a satellite is complex,there are many detail and considerate problems need to be considered. This will also be the in-depth research work in future.
| [1] | Lindsay, E. Canadian space robotics on board the international space station. 2005 CCToMMSymposium on Mechanisms, Machines, and Mechatronics, Canadian Space Agency, Montreal,Canada, 26–27 (2005) |
| [2] | Iwata, T. Recent Japanese activities in space automation & robotics—an overview. Proceeding ofthe 6th International Symposium on Artificial Intelligence and Robotics & Automation in Space:i-SAIRAS 2001, Canadian Space Agency, Quebec, Canada (2001) |
| [3] | Ge, X. S., Chen, L. Q., and Lü, J. Nonholonomic motion planning of a space manipulator systemusing genetic algorithm (in Chinese). Journal of Astronautics, 26(3), 262–266 (2005) |
| [4] | Zhang, D. G. Recursive Lagrangian dynamic modeling and simulation of multi-link spatial flexiblemanipulator arms. Applied Mathematics and Mechanics (English Edition), 30(10), 1283–1294(2009) DOI 10.1007/s10483-009-1008-2 |
| [5] | Li, J. F. andWang, Z. L. Study on attitude dynamics of a liquid-filled spacecraft with manipulators(in Chinese). Journal of Astronautics, 20(2), 81–86 (1999) |
| [6] | Liang-Boon, W. and Michael, W. W. On the dynamics of contact between space robots andconfiguration control for impact minimization. IEEE Transactions on Robotics and Automation,9(5), 581–591 (1993) |
| [7] | Guo, Y. S. and Chen, L. Terminal sliding mode control for coordinated motion of space rigidmanipulator with external disturbance. Applied Mathematics and Mechanics (English Edition),29(5), 583–590 (2008) DOI 10.1007/s10483-008-0503-1 |
| [8] | Dong, Q. H. and Chen, L. The dynamic and robust control of space robot during capture operation.The 23rd International Congress of Theoretical and Applied Mechanics (ICTAM2012), Beijing,China, 9–24 (2012) |
| [9] | Slotin, J. E. and Li, W. P. On the adaptive control of robot manipulators. Journal of the RoboticsResearch, 6(3), 49–59 (1987) |
 2014, Vol. 35
2014, Vol. 35






































