Shanghai University
Article Information
- ZHI-YONG ZHANG, YU-SHU CHEN. 2014.
- Harmonic balance method with alternating frequency/time domain technique for nonlinear dynamical system with fractional exponential
- Appl. Math. Mech. -Engl. Ed., 35(4): 423-436
- http://dx.doi.org/10.1007/s10483-014-1802-9
Article History
- Received 2013-03-08;
- in final form 2013-06-13
All periodic motion of linear dissipation system is stable. However,some periodic motion fornonlinear dissipation system is unstable. There may be many different types of motion,such assuper-harmonic,sub-harmonic,and chaotic vibrations. The analysis of motion types and stableregions of engineering system has important significance. It is common to use the fractionalexponential model to describe impact and contact problems in engineering[1]. However,thedynamic response of this model is difficult for theoretical analysis[2]. Therefore,it is necessaryto find an effective method for these problems.
A semi-analytical method of implicit harmonic balance analysis named the harmonic balancemethod with alternating frequency/time (HB-AFT) domain technique was first proposed byYamauchi in 1983[3]. Kim and Noah[4, 5, 6] developed this method to a complete solution strategyfor the periodic response of dynamic systems. The homotopy continuation scheme togetherwith the HB-AFT method was provided to compute hysteresis response by Groll and Ewins[7].Tiwari and Gupta[8] first used the HB-AFT method to the bearing-rotor systems consideringball passage vibrations to validate the steady response obtained by numerical integration. Villaet al.[9] used a whole frequency domain method based on the HB-AFT and a perturbationmethod to study the response characteristic in a flexible ball bearings-rotor system. However,it should be noted that this whole frequency domain method in Ref. [9] cannot generate thebifurcation mechanism of instability locations.
In this paper,we present the advantage of the HB-AFT method for fractional exponentialproblems. The global response of a two degree-of-freedom ball bearing-rotor structure is deeplyanalyzed by the HB-AFT approach combined with the Floquet theory,and for the first time,weattempt to estimate the dangerous unstable ranges of with this system via the above schemes. 2 Comparison of solving methods
There are many numerical and analytical methods for the study of steady state of differentialdynamical systems. Usually,we take the problems as initial value problems of ordinarydifferential equations and solve the systems with numerical integration. The Runge-Kutta(R-K) method is among the most popular classes of formulas for the numerical integrationof initial value problems. Unlike the multi-step methods,it is a one-step method,and onecan change the step size of integration as often and by as much as required. Therefore,it isusually effective for stiff equations[10],although a higher-order R-K method requires more functionevaluations per integration step. However,the R-K method only can obtain asymptoticsteady-state response,and it may take a long time of integration for a system with a smallerdamping[4]. Furthermore,the initial value problems cannot be used to obtain the unstable periodicresponse[11]. This brings difficulties for the analysis of the bifurcation characteristics ofperiodic motion. The resolution of the responses of dynamic systems can also be converted toa boundary-value problem. Then,one can use the shooting method or finite-difference schemesto solve the problem. The shooting algorithm and its modified methods[12, 13, 14] are widely usedin engineering[15, 16]. However,the initial value and the integration step-size have a great effecton the convergence and the convergent speed[17, 18]. Moreover,a heavy computation is oftenneeded,especially when the period of the system’s response is very large,e.g.,in some casesdealing with multiple-input frequencies[19].
In terms of analytical methods,the common methods,such as the small parameter method,the average method,and the multi-scale method,are effective for characteristics investigationof weakly nonlinear systems. When dealing with strong nonlinearity,the harmonic balancemethod is usually used. However,the calculation accuracy is hard to ensure[17, 20].
All methods developing from the classic harmonic balance (HB) method,e.g.,the incrementalharmonic balance (IHB) method,the HB-AFT method,and the generalized harmonicbalance (GHB) method,can provide periodic solutions in form of trigonometric series. The IHBmethod was first proposed by Lau and Cheung in 1981[21]. The basic idea of the approach isas follows: first,suppose the solution to the system is harmonic; then,deduce the incrementalequation of the harmonic coefficients; finally,obtain the result by the iteration of the incrementalequation. The IHB method is very effective in analyzing the periodic behaviors of smoothdynamics[22],and it can be used to deal with piecewise-linear problems[23, 24]. However,becauseof the incremental equation of the system usually obtained by Taylor series expansion[25],thismethod is difficult to deal with nonlinear systems with piecewise discontinuity from the mathematicaldefinition[26, 27]. In recent years,the GHB method has been developed by Luo[28, 29].The authors,by the averaging idea,set the solution to the system with harmonic terms andsupposed that the coefficients of these terms vary slowly with time. The algebraic equationsof the coefficients were obtained by harmonic balance process,and the solutions were derivedby any iteration strategy. These solutions and their bifurcation behaviors could be determinedfrom the analysis of the stability about the equilibrium point by a perturbation of the harmonicterms. The GHB method provides an analysis tool for chaos systems[28]. However,because ofthe average idea[30],the nonlinear function should be integrated in the process of computation,which makes it a challenge for the problem with complicated integration.
For nonlinear systems,the main idea of the HB-AFT is as follows:
To analyze its periodic solution property,it is assumed that x(t) = x(t+T ),where T represents the period of x(t). Then,x(t) and f(·) can be written as two groups of Fourier series expansionswith the same orthogonal basis. According to Eq. (1),one can get an implicitly nonlinearalgebraic relationship between the harmonic coefficients of x(t) and f(·). With the aid ofthe discrete Fourier transform (DFT) and the inverse discrete Fourier transform (IDFT),theinformation used to iterate the implicitly algebraic can be obtained. Thus,it can be seen thatthe HB-AFT method is different from the IHB method and the GHB method. It establishesrelationships of each order harmonic term directly from the discrete time frequency features,and there is little integration and analytical work required during the solving processe of theHB-AFT method. Thus,this method can be considered to be more versatile for the strongnonlinear problems with piecewise fractional exponential. 3 Model and methods 3.1 Bearing-rotor model
For the ball bearing,as shown in Fig. 1,when only consider the effects of Hertz contact andball passage vibrations on the bearing-rotor system,the classical 2-DOF model of ball bearingis enough for the qualitative analysis[31]. Thus,the constitutive equation of a rigid rotor withthe ball bearing is expressed as
where and G(·) is a Heaviside function. Here, |
| Fig. 1 Schematic diagram of ball bearing model |
In the above equations,m is the mass of the rotor and the inner ring,C is the systemdamping,Cb is the Hertz contact stiffness between the balls and the inner-outer rings,δi is theith small displacement between the ith ball and the bearing raceway,δ0 is the radial clearanceof the bearing,W is the weight supported by the outer ring,ω is the angular velocity of therotor shaft,θi is the instant angular location of the ith ball,ωc is the cage angular velocity,Nb is the number of balls,ri and ro are the radii of the inner and the outer rings,and G(·)takes · and 0 representing the contact and non-contact cases between a ball and the outer ring,respectively.
According to the similarity theory[30],define τ=ωct and denote ()′ by differentiation withrespect to τ. Then,Eq. (2) can be transformed into
where Here,
From Eqs. (3) and (4),one can see the problem,dealt with in this article,is a parametricallyexcited system with the multiple piecewise G( ),where G(
),where G( ) is also a complicated function.Therefore,the common analytical method is not available for this problem[32].
3.2 HB-AFT scheme
) is also a complicated function.Therefore,the common analytical method is not available for this problem[32].
3.2 HB-AFT scheme
Firstly,do the process of harmonic balance to Eq. (3).
The periodic solution forms of x and y can be represented as
The nonlinear restoring forces of fx(x,y,τ) and fy(x,y,τ) can be also written as In Eqs. (5) and (6),K represents the maximum number of the considered harmonic terms.Substituting Eqs. (5) and (6) into Eq. (3) and balancing the coefficients of each order harmonic, one can obtain the algebraic equations g. For the constant terms,
For the cosine terms,For the sine terms,
In the above equations,k= 1,2,· · · ,K.Let
where P and Q represent the coefficients of harmonics of displacements and nonlinear restore forces,respectively.Take P as an unknown variable. Using Eqs. (5)-(7),one can iterate to find the fix point P.Here,the Newton-Raphson method is taken for the iteration,that is,
where J is the Jacobian matrix,i.e.,J =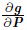
After the process of harmonic balance,the values of Q and J in each step of iterations canbe obtained by the alternating frequency/time (AFT) technique. For a supposed P,an IDFT is first used to obtain discrete values of x(τ) and y(τ),
where n = 0,1,· · · ,N. Here,x(n) and y(n) denote the sampled points at the nth discrete time,i.e.,x(n△T) and y(n△T ),where △T = 2π/N,and N is the number of samples in the timedomain.According to Eqs. (4) and (10),the nonlinear restoring forces fx(x,y,T) and fy(x,y,T) can be discreted into
The discrete values of fx(x,y,T) and fy(x,y,T) in the frequency domain can be obtained by the DFT as Q,that is, where k = 1,2,· · · ,K. According to Eq. (7) and Eqs. (10)-(12),the elements of J in Eq. (9) can be deduced into whereBy combining the process of harmonic balance and AFT,the iterations of Eq. (9) can readily yield P in proper accuracy. The procedure is as follows:
(i) For a supposed P(0),obtain Q(0) and J(0) by using Eqs. (10),(12),and (13).
(ii) Iterate Eq. (9) once,and get P(1).
(iii) Continue (i) and (ii) until the norm of P(m)-P(m−1) is less than an allowed ε". 3.3 Stability analysis
In order to make a systematic study on the bifurcation characteristics of the system,one needs to analyze the stability of the periodic solutions obtained by the HB-AFT. In this study,the Floquet theory is employed[17, 20, 25],and the method developed by Hsu is applied for approximating the monodromy matrix. Here,from the characteristics of the HB-AFT,a simplified strategy on the base of Hsu’s method can be proposed[33].
Let
Then,Eq. (3) can be transformed into Define A(T,U(T)) as whereFor the system of Eq. (14),give △U to perturb the assumed equilibrium U* and have
Then,the stability of U* can be obtained by the linear stability of △U in the following system: According to Hsu’s method,the approximating monodromy matrix can be expressed as[22] Here,I denotes the identity matrix,and a constant matrix An substitutes the time-varying matrix A(T,U(T) in the nth time interval,that is, whereCombining the HB-AFT process,we get
The substitution has been done for two reasons. First,some of the systems have complicated equation forms. Taking Eq. (20) rather than Eq. (19) can avoid the difficulties of complicated integrations. For instance,the problem of Eq. (15) studied here has multiple piecewise irrational functions of G(δi(n))0.5,where i = 1,2,· · · ,Nb. These functions are very hard to integrate. Second,this simplification can maintain internal consistency of discretization of the HB-AFT scheme. The elements of A(T,U(T)) are components of the elements of the Jacobian matrix elements (see Eq. (13)),which can reduce the work of the programming calculation. 4 Results and discussionThe rotor bearing system under analysis is shown in Eq. (3). The reference values in the equation are from Ref.[8] as follows:
From Eq. (3),one can see that the studied model is a parametrical excited system,and T = 2π/Ω is the excited period,where Ω is the revolution angular velocity of the balls. When K = 36 (in Eq. (5)),N = 144 (in Eq. (10)),ε = 10-19,and Ω= 500 rad/s,the analytical approximation of the period-1 solution obtained by the HB-AFT method is (here,the harmonic terms,whose coefficients are less than 10−18,are not presented) where Ωvc = NbΩ. The above expression of x(t) suggests that the period-1 motion of the system is affected by the ball passage vibrations. Actually,the minimum period of the motion is Tvc rather than T ,where Tvc = 2π/Ωvc. Here,fvc = 1/Tvc is usually called the varying compliance frequency [16].As shown in Fig. 2,the HB-AFT results agree well with the numerical solutions of the fourth-order R-K method. The calculation of the HB-AFT has a fast convergence and a large convergent region,which can be seen in Fig. 3. In Fig. 3,the HB-AFT with initial iterative values of P(0) = [0] except P(0)(1) = 1.0 via the 5th iteration has arrived at a solution close to the R-K integration corresponding to the round markers.
 |
| Fig. 2 Phase portrait of period-1 solution when Ω= 500 rad/s |
 |
| Fig. 3 Convergence of HB-AFT results under increasing iteration times |
In order to analyze system’s global periodic characteristics,taking Ω as a control parameter,using the HB-AFT method,search the period-1 solutions between 480 rad/s and 1 000 rad/s with a step-size of 10 rad/s. By the simplified method shown in Section 3.3,the stability of the obtained solutions of period-1 is analyzed by the Floquet theory. It is found that the Floquet multipliers keep a convergent accuracy to 0.01 with N = 2 × 104 and nj = 5 (in Eq. (18)). Calculations show that the leading multipliers are inside the unit circle at Ω = 480 rad/s to 690 rad/s,and the corresponding period-1 solutions are stable. From 700 rad/s to 950 rad/s,the leading multipliers are less than -1. Hence,the corresponding period-1 solutions are unstable. Until Ω = 960 rad/s,the leading multipliers come back to the unit circle from the negative real axis. Table 1 further indicates that the period doubling bifurcations occur in the angular velocity ranges of Ω from 697 rad/s to 698 rad/s and from 953 rad/s to 954 rad/s,which is basically consistent with the numerical result shown in Fig. 4.
 |
 |
| Fig. 4 Bifurcation diagrams versus parameter Ω and bifurcation locations of period-1 motion obtained by HB-AFT with Floquet theory |
Note the fact that the period doubling bifurcation induces the instability of period-1 motion. Hence,in order to do deep investigation for dynamical behaviors of the system,it is necessary to analyze the response of period-2 motion in the range from 700 rad/s to 950 rad/s,which is unstable for period-1 motion. For example,when K = 36,N = 144,ε = 10-19,and Ω = 930 rad/s,the analytical approximation of the period-2 solution obtained by the HB-AFT method is (here the harmonic terms,whose coefficients are less than 10-18,are not presented)
The result is close to the numerical simulation (see Fig. 5(a)),and this indicates that the system has period-2 motion at Ω = 930 rad/s. As displayed in the above expressions of x(t) and y(t),the period-2 motion of the system is also affected by the ball passage vibrations. Actually,the minimum period of the motion is 2Tvc rather than T ,which coincides with the power spectra shown by Fig. 5(b).
Using the present method,we continue to investigate the stability of the global period- 2 motion of the system. The analysis indicates that the dynamical characteristics of period-2 motion are also interval stability,and the period doubling bifurcation is also a way to instability. However,Table 2 presents the case that two complex conjugate Floquet multipliers leave the unit circle,which indicates that the Neimark bifurcation[11, 25] occurs from Ω = 925 rad/s to 928 rad/s. Figure 6 shows that the Poincaré maps are built by the R-K method at Ω = 926 rad/s,927 rad/s,and 928 rad/s. It is clear that the motion changes from quasi-periodic to periodic gradually,which is a strong evidence for the Neimark bifurcation in the period-2 motion.
Figure 7(a) presents the global peak value characteristics of the period-1 and period-2 solutions by Ω as the horizontal axis. The peak of x(t) is calculated by the HB-AFT as a function,where the square markers and the round markers correspond to the solutions to period-1 and period-2,respectively. In Fig. 7(a),the area of A-A denotes the unstable velocity range of period-1 motion,and the three darker areas,i.e.,B-B,C-C,and D-D,signify the unstable velocity ranges of period-1 and period-2 simultaneously. In these three areas,one can predict that the forms of motion are more complicated,and the chaotic motion may occur. The rotor bearing system would avoid working in these ranges. In fact,the largest Lyapunov exponent curve in Fig. 7(b) clearly indicates that the chaotic motion exists in the ranges of B-B,C-C,and D-D. Figure 8 affirms the existence of chaos in these ranges to be right further. It can be seen that the above process is an effective way to estimate the dangerous ranges of the system’s motion.
Compared with other common methods,the HB-AFT method requires fewer analysis,especially the studies of integration and series expansion,during the solving processes. Thus,this method is well-suited for the fractional exponential problems,even the problem with piecewise-irrational nonlinearities. It is also an efficient method because of its property of fast convergence in a large range.
Using the HB-AFT method,a rigid rotor-ball-bearing system is analyzed. The analysis indicates that the dynamical characteristics of periodic motion are interval stability,and the period doubling bifurcation and the Neimark bifurcation are two ways to instability for the system.
Besides,combining the treatment of the HB-AFT method,a simplified strategy to determine the Floquet multipliers is proposed. A way to give a fast estimation of the dangerous motion range is presented,which may be significant for the global response analysis and the dynamic optimal design of the nonlinear systems.

Fig. 5 Orbit of system and power spectra of x(t) with Ω
= 930 rad/s 

Fig. 6 Poincaré maps of x(t) at 926 rad/s,927 rad/s,and 928 rad/s 
Fig. 7 Peak diagrams of global period-1 solution and period-2 solution,obtained by HB-AFT and largest Lyapunov exponent curve calculated by Wolf method[34]

Fig. 8 Poincaré maps of x(t) response at 710 rad/s,820 rad/s,and 910 rad/s
Acknowledgements
We gratefully acknowledge Professor A. C. J. LUO for many valuable suggestions to this work during his seminars in Harbin,China.
| [1] | Jin, D. P., Hu, H. Y., and Wu, Z. Q. Analysis of vibro-impacting flexible beams based on Hertziancontact model (in Chinese). Journal of Vibration Engineering, 11(1), 46–51 (1998) |
| [2] | Yigit, A. S., Ulsoy, A. G., and Scott, R. A. Spring-dashpot models for the dynamics of a radicallyrotating beam with impact. Journal of Sound and Vibration, 142(3), 515–525 (1990) |
| [3] | Yamauchi, S. The nonlinear vibration of flexible rotors. Transaction of JSME, Series C, 446,1862–1868 (1983) |
| [4] | Kim, Y. B. and Noah, S. T. Stability and bifurcation analysis of oscillators with piecewise-linearcharacteristics: a general approach. ASME Journal of Applied Mechanics, 58(2), 545–553 (1991) |
| [5] | Kim, Y. B. and Noah, S. T. Response and bifurcation analysis of an MDOF rotor system with astrong nonlinearity. Nonlinear Dynamics, 2, 215–234 (1991) |
| [6] | Kim, Y. B. and Noah, S. T. Quasi-periodic response and stability analysis for a non-linear Jeffcottrotor. Journal of Sound and Vibration, 190(2), 239–253 (1996) |
| [7] | Groll, G. V. and Ewins, D. J. The harmonic balance method with arc-length continuation inrotor/stator contact problems. Journal of Sound and Vibration, 241(2), 223–233 (2001) |
| [8] | Tiwari, M. and Gupta, K. Effect of radial internal clearance of a ball bearing on the dynamics ofa balanced horizontal rotor. Journal of Sound and Vibration, 238(5), 723–756 (2000) |
| [9] | Villa, C., Sinou, J. J., and Thouverez, F. Stability and vibration analysis of a complex flexiblerotor bearing system. Communications in Nonlinear Science and Numerical Simulation, 13, 804–821 (2008) |
| [10] | Cash, J. R. and Karp, A. H. A variable order Runge-Kutta method for initial value problems withrapidly varying right-hand sides. ACM Transactions on Mathematical Software, 16(3), 201–222(1990) |
| [11] | Nayfeh, A. H. and Balachandran, B. Applied Nonlinear Dynamics, Wiley InterScience, New York(1995) |
| [12] | Ling, F. H. A numerical treatment of the periodic solutions of non-linear vibration systems. AppliedMathematics and Mechanics (English Edition), 4(4), 525–546 (1983) DOI 10.1007/BF01874666 |
| [13] | Hu, H. Y. Numerical scheme of locating the periodic response of non-smooth non-autonomoussystems of high dimension. Computer Methods in Applied Mechanics and Engineering, 123(1),53–62 (1995) |
| [14] | Li, D. X. and Xu, J. X. Periodic solution and its approximate analytic expressions of the nonlinearrotor bearing system (in Chinese). Chinese Journal of Computational Mechanics, 21(5), 557–563(2004) |
| [15] | Choi, S. K. and Noah, S. T. Response and stability analysis of piecewise-linear oscillators undermulti-forcing frequencies. Nonlinear Dynamics, 3, 105–121 (1992) |
| [16] | Bai, C. Q., Xu, Q. Y., and Zhang, X. L. Nonlinear stability of balanced rotor due to effect of ballbearing internal clearance. Applied Mathematics and Mechanics (English Edition), 27(2), 175–186(2006) DOI 10.1007/s10483-006-0205-1 |
| [17] | Zhou, J. Q. and Zhu, Y. Y. Nonlinear Vibrations (in Chinese), Xi’an Jiao Tong University Press,Xi’an (1998) |
| [18] | Press, W. H., Teukolsky, S. A., Vellering, W. T., and Flannery, B. P. Numerical Recipes in Fortranthe Art of Scientifc Computing, 2nd ed., Cambridge University Press, Cambridge (1992) |
| [19] | Chua, L. O. and Akio, U. Algorithms for computing almost periodic steady state response ofnonlinear systems to multiple input frequencies. IEEE Transactions on Circuits and Systems, 28,953–971 (1981) |
| [20] | Chen, Y. S. Nonlinear Vibrations (in Chinese), Higher Education Press, Beijing (2002) |
| [21] | Lau, S. L. and Cheung, Y. K. Amplitude incremental variational principle for nonlinear vibrationof elastic systems. ASME Journal of Applied Mechanics, 48, 959–964 (1981) |
| [22] | Shen, J. H., Lin, K. C., Chen, S. H., and Sze, K. Y. Bifurcation and route-to-chaos analyses forMathieu-Duffing oscillator by the incremental harmonic balance method. Nonlinear Dynamics,52, 403–414 (2008) |
| [23] | Aghothama, A. R. and Arayanan, S. N. Bifurcation and chaos in geared rotor bearing system byincremental harmonic balance method. Journal of Sound and Vibration, 226(3), 469–492 (1999) |
| [24] | Yang, S. P. and Shen, Y. J. Nonlinear dynamics of gear system based on incremental harmonicbalance method (in Chinese). Journal of Vibration and Shock, 24(3), 40–42 (2005) |
| [25] | Hu, H. Y. Applied Nonlinear Dynamics (in Chinese), Aviation Industry Press, Beijing (2000) |
| [26] | Zorich, V. A. Mathematical Analysis II, Springer, Berlin (2002) |
| [27] | Cameron, T. M. and Griffin, J. H. An alternating frequency/time domain method for calculatingthe steady state response of nonlinear dynamic systems. ASME Journal of Applied Mechanics, 56,149–154 (1989) |
| [28] | Luo, A. C. J. Continous Dynamical Systems, Higher Education Press, Beijing (2012) |
| [29] | Luo, A. C. J. Regularity and Complexity in Dynamical Systems, Springer-Verlage, New York (2012) |
| [30] | Arnold, V. I. Mathematical Methods of Classical Mechanics, 2nd ed., Springer-Verlag, New York(1991) |
| [31] | Liew, A., Feng, N., and Hahn, E. J. Transient rotordynamic modeling of rolling element bearingsystems. Journal of Engineering for Gas Turbines and Power, 124, 984–991 (2002) |
| [32] | Gao, S. H., Long, X. H., and Meng, G. Nonlinear response and nonsmooth bifurcations of anunbalanced machine-tool spindle-bearing system. Nonlinear Dynamics, 54, 365–377 (2008) |
| [33] | Friedmann, P. and Hammond, C. E. Efficient numerical treatment of periodic systems with ap-plication to stability problems. International Journal for Numerical Methods in Engineering, 11,1117–1136 (1977) |
| [34] | Wolf, A., Swift, J. B., Swinney, H. L., and Vastano, J. A. Determining Lyapunov exponents froma time series. Physica D, 16, 285–317 (1985) |
 2013, Vol. 35
2013, Vol. 35



































