Shanghai University
Article Information
- ZHEN-YU ZHANG. 2014.
- Improved modal truncation method for eigensensitivity analysis of asymmetric matrix with repeated eigenvalues
- Appl. Math. Mech. -Engl. Ed., 35(4): 437-452
- http://dx.doi.org/10.1007/s10483-014-1803-6
Article History
- Received 2012-07-24;
- in final form 2013-05-31
Matrix eigensensitivity analysis has extensive applications to identification,modification,re-analysis,vibration control,and optimization design of dynamic systems. Early works wereconcentrated on the sensitivity analysis of matrices with simple eigenvalues. In some problemssuch as dynamics of symmetric structures,however,the corresponding matrices can have repeatedeigenvalues. More importantly,many systems with clusters of frequencies can occurin practical engineering. For example,during system optimization,some originally separatedfrequencies may approach closer and closer. The direct eigensensitivity analysis of a systemwith clusters of frequencies is difficult and inefficient,but the problem can be solved efficientlyand accurately by reducing it to the perturbation problem of a proper system with repeatedfrequencies[1].
Most of the early works of eigensensitivity analysis were on the self-adjoint systems suchas the undamped dynamic systems or damped dynamic systems with proportional damping.However,in some problems such as the dynamics of damped systems with non-proportional damping,or more generally,the dynamics of fluid-structure coupled systems where the mass,damping,and stiffness matrices can be asymmetric,we often have to perform eigensensitivityanalysis of asymmetric matrices. In these cases,when the mass matrix is non-singular,thecorresponding quadratic eigenvalue problem can be reduced to a standard eigenvalue problemof an asymmetric matrix.
The method of eigensensitivity analysis can mainly be divided into two categories. One isthe direct or algebraic method which only involves the eigenpairs to be differentiated. It is themost efficient method for large systems when the number of the eigenpairs to be differentiatedis very small. But this method needs to calculate generalized inverses of singular matrices andis inefficient for large systems when the number of the eigenpairs to be differentiated is notvery small. Nelson[2],Ojalvo[3],Mills-Curran[4],Dailey[5],Friswell[6, 7],Lee et al.[8, 9, 10],Wei andZhang[11],Lee et al.[12, 13],and Choi et al.[14, 15] developed the direct methods for eigensensitivityanalysis of self-adjoint systems. Liu[16],Adhikari and Friswell[17],Najeh et al.[18, 19],and Xuet al.[20] extended the methods to non-self-adjoint systems with simple eigenvalues. Luongo[21]and Zhang and Zhang[22, 23, 24] extended the methods further to defective systems. The othercategory is the indirect or modal expansion method which needs to use all of the eigenpairsof the unperturbed system. It is very expansive and impractical for large systems,but it isthe foundation of various approximate and iterative methods. Fox and Kapoor[25],Murthyand Haftka[26],Juang et al.[27],Bernard and Bronowicki[28],and Zhang and Wei[29] developedthe modal expansion methods for eigensensitivity analysis of self-adjoint systems. Adhikariand Friswell[30] and Adhikari[31] extended the methods to non-self-adjoint systems with simpleeigenvalues. Zhang and Zhang[32] and Zhang[33] extended the methods further to defectivesystems.
The improved modal truncation methods for eigensensitivity analysis developed in recentyears only need to use parts of the eigenpairs of the unperturbed system. Therefore,they aremore efficient and more practical for large systems. Wang[34] proposed a first-order approximatemethod for calculating the first-order eigenvector derivatives of an undamped symmetricsystem with simple eigenvalues. Zhao et al.[1] extended the method to an undamped symmetricsystem with repeated eigenvalues. Zeng[35] developed a second-order approximate methodfor calculating the first-order eigenvector derivatives of a viscous damping system with simpleeigenvalues by reducing the quadratic eigenvalue problem to a linear eigenvalue problem of anasymmetric matrix whose order is twice of the degree-of-freedom of the original problem. Kimet al.[36] developed an approximate method for calculating the first-order eigenvector derivativesof a self-adjoint system with simple eigenvalues based directly on the quadratic eigenvalue problem.Based directly on the original quadratic eigenvalue problem,Moon wt al.[37] extended themethod to a non-self-adjoint system with simple eigenvalues,which can calculate the first-ordereigenvector derivatives.
In this paper,an improved modal truncation method with arbitrarily high order accuracy isdeveloped for calculating the second- and third-order eigenvalue derivatives and the first- andsecond-order eigenvector derivatives of an asymmetric and non-defective matrix with repeatedeigenvalues. 2 Exact modal expansion method
We investigate the eigensensitivity of an n × n non-defective and non-singular matrix A.The assumption that A is non-singular is not essential because when A is singular,instead oftreating A,we can treat
where α is any constant which makes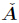 non-singular. Let λ1,λ2,···,λr be the eigenvalues of A with the multiplicities m(1),m(2),···,m(r),respectively. Let υ(i,1),u(i,2),···,u(i,m(i)) be the linearly independent eigenvectors of A associated with λi(i= 1,2,···,r). Let υ(i,1),υ(i,2),···,υ(i,m(i)) be the linearly independent left eigenvectors of A associated with λi,which are orthogonalizedand normalized with respect to υ(i,1),υ(i,2),···,υ(i,m(i)) so that
where the superscript “H ” denotes the transpose and complex conjugate of a matrix,and δj,k is the Kronecker’s notation. Define
Then,we have
where Im(j) is the unit matrix of the order m(j) (j= 1,2,···,r).
non-singular. Let λ1,λ2,···,λr be the eigenvalues of A with the multiplicities m(1),m(2),···,m(r),respectively. Let υ(i,1),u(i,2),···,u(i,m(i)) be the linearly independent eigenvectors of A associated with λi(i= 1,2,···,r). Let υ(i,1),υ(i,2),···,υ(i,m(i)) be the linearly independent left eigenvectors of A associated with λi,which are orthogonalizedand normalized with respect to υ(i,1),υ(i,2),···,υ(i,m(i)) so that
where the superscript “H ” denotes the transpose and complex conjugate of a matrix,and δj,k is the Kronecker’s notation. Define
Then,we have
where Im(j) is the unit matrix of the order m(j) (j= 1,2,···,r).
Suppose that A is perturbed to A(ε),where A(ε) is an arbitrary analytic function of the small parameter ε and satisfies the condition that A(0) = A. Write the eigenvalue problem of A(ε) by
where λ(ε) and ω(ε) are,respectively,the eigenvalue and eigenvector of A(ε).Now,we investigate the variations of an eigenvalue λi and its corresponding eigenvectors in the eigenspace spanned by the columns of U(i) (1≤i≤r) when A is perturbed to A(ε). When ε = 0,Eq. (7) becomes
Thus,in the eigenspace associated with the eigenvalue λi a differentiable eigenvector ω(0) can be denoted by where d is an undetermined non-zero vector of the dimension m(i). In the following,we write the lth-order (l≥1) derivatives ofA(ε),λ(ε),ω(ε),and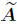 (ε) by A(l)(ε),λ(l)(ε),ω(l)(ε),and
(ε) by A(l)(ε),λ(l)(ε),ω(l)(ε),and 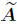 (l)(ε),where
and write A(l)(0),λ(l)(0),ω(l)(0),and
(l)(ε),where
and write A(l)(0),λ(l)(0),ω(l)(0),and 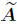 (l)(0) by A(l),λ(l),ω(l),and
(l)(0) by A(l),λ(l),ω(l),and 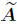 (l) (l = 1,2,···). Differentiating both sides of Eq. (7) with respect to ε,we obtain
When ε = 0,we have
To evaluate w(t) for t≥1,we perform its modal expansion,i.e.,
where c(t,k) is an undetermined vector of the dimension m(k) (k = 1,2,···,r; t = 1,2,···). Substituting Eq. (12) with t = 1 into Eq. (11) and using Eq. (9),we obtain
Pre-multiplying both sides of Eq. (13) by V (i)H,we obtain
Equation (14) is an eigenvalue problem of the m(i) × m(i) matrix V (i)HA(1)U(i) with λ(1) as its eigenvalue and d as its corresponding eigenvector. In this paper,it is assumed that all of the eigenvalues of Eq. (14) are simple.
(l) (l = 1,2,···). Differentiating both sides of Eq. (7) with respect to ε,we obtain
When ε = 0,we have
To evaluate w(t) for t≥1,we perform its modal expansion,i.e.,
where c(t,k) is an undetermined vector of the dimension m(k) (k = 1,2,···,r; t = 1,2,···). Substituting Eq. (12) with t = 1 into Eq. (11) and using Eq. (9),we obtain
Pre-multiplying both sides of Eq. (13) by V (i)H,we obtain
Equation (14) is an eigenvalue problem of the m(i) × m(i) matrix V (i)HA(1)U(i) with λ(1) as its eigenvalue and d as its corresponding eigenvector. In this paper,it is assumed that all of the eigenvalues of Eq. (14) are simple.
Let λ(1,1),λ(1,2),···,λ(1,m(i)) be the eigenvalues of Eq. (14) and { (1),
(1), (2),···,
(2),···, (m(i))} be any set of the corresponding linearly independent eigenvectors. Define
(m(i))} be any set of the corresponding linearly independent eigenvectors. Define
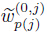 be the first among the components of e
be the first among the components of e 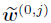 (j = 1,2,···,m(i)) with the largest absolute value.
(j = 1,2,···,m(i)) with the largest absolute value.
Define
Then,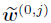 satisfies the normalization condition that
satisfies the normalization condition that 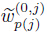 ,the first among the components of w(0,j) (j = 1,2,···,m(i)) with the largest absolute value,is 1,i.e.,
Then,w(0,j) satisfies the normalization condition that wp(j)(0,j) ,the first among the components of w(0,j) (j = 1,2,···,m(i)) with the largest absolute value,is 1,i.e.,
,the first among the components of w(0,j) (j = 1,2,···,m(i)) with the largest absolute value,is 1,i.e.,
Then,w(0,j) satisfies the normalization condition that wp(j)(0,j) ,the first among the components of w(0,j) (j = 1,2,···,m(i)) with the largest absolute value,is 1,i.e.,
Define
Then,we haveNow,for any j ≤ m(i),we investigate the evaluation of the eigenvalue and eigenvector derivatives associated with
For notation simplification,here we still denote the perturbed eigenvalue λi,j(ε) and the eigenvector wi,j(ε),respectively,by λ(ε) and w(ε). Note that if the perturbed eigenvector w(ε) is so normalized that wp(j)(ε),the corresponding component of w(ε),is 1,then for any k ≥ 1,wp(j)(k),the corresponding component of w(k),is zero,i.e.,Pre-multiplying both sides of Eq. (13) by V (l)H (≠i),we obtain the coefficient c(1,l) in Eq. (12) for w(1) as follows: Define the known quantity
Then,we have Differentiating both sides of Eq. (10) with respect to ε,we obtain When ε = 0,by using Eq. (21),Eq. (22) becomes where Substituting Eq. (12) with t = 2 into Eq. (23),we obtain Pre-multiplying both sides of Eq. (24) by V (i)H and using Eq. (18),we obtain Pre-multiplying both sides of Eq. (25) by D−1 and noting that d = d(j) is the jth-column of D,we have where and e(j) is the jth-column of Im(i). Comparing the jth-component on both sides of Eq. (26) and noting that λ(1) = λ(1,j) is the jth-diagonal element of the diagonal matrix ∧(1),we get Comparing the kth-component (k≠j) on both sides of Eq. (26),we get the kth-component of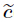 (1,i) as follows:
(1,i) as follows:
By use of Eq. (17),Eq. (21) can be re-written as
Comparing the p(j)th-component on both sides of Eq. (29) and using the conditions that wp(j)(1) = 0 and wp(j)(0,j) = 1,we can get the jth-component of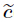 (1,i) as follows:
where
(1,i) as follows:
where 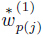 is the jth-component of
is the jth-component of 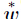 (1) . Thus,
(1) . Thus,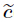 (1,i) is completely determined. Therefore,c(1,i) = D
(1,i) is completely determined. Therefore,c(1,i) = D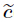 (1,i) and w(1) can in turn be determined.
(1,i) and w(1) can in turn be determined.Pre-multiplying both sides of Eq. (24) by V (<>il)H (l≠i),we obtain
Define Then,we have Differentiating both sides of Eq. (22) with respect to ε,we obtain When ε = 0,by using Eq. (32),Eq. (33) becomes where Substituting Eq. (12) with t = 3 into Eq. (34),we obtain Pre-multiplying both sides of Eq. (35) by V(i)H and using Eq. (18),we obtain where Comparing the jth-component on both sides of Eq. (36),we obtain Comparing the kth-component (k≠j) on both sides of Eq. (36),we get the kth-component of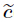 (2,i) as follows:
(2,i) as follows:
By using Eq. (17),Eq. (32) can be re-written as
Comparing the p(j)th-component on both sides of Eq. (39) and using the conditions that we get Thus,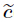 (2,i) is completely determined. Therefore,c(2,i) = D
(2,i) is completely determined. Therefore,c(2,i) = D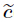 (2,i),and w(2) can in turn be determined. By the similar way,the higher order eigenvalue and eigenvector derivatives can also be determined step by step.
3 Improved modal truncation method
(2,i),and w(2) can in turn be determined. By the similar way,the higher order eigenvalue and eigenvector derivatives can also be determined step by step.
3 Improved modal truncation method
Let the different eigenvalues of A be arranged so that
We choose s(s<r) that satisfies the conditionNow,we investigate the modal truncation method for calculating the eigenvalue and eigenvector derivatives associated with eigenvalue λi(i≤s) and the differentiable eigenvector
As before,we briefly write w(0),λ(1),and d for w(0,j),λ(1,j),and d(j),respectively. It is known from the preceding analysis that w(1),the first-order derivative of the differentiable eigenvector w(0),can be expressed by Eq. (21),where and On the rightest side of Eq. (44), In the derivation of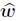 (q,1),Eq. (6),the spectral decomposition of A,has been used. The computation of
(q,1),Eq. (6),the spectral decomposition of A,has been used. The computation of 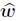 (q,1) can be written in the iterative form as follows:
Thus,
(q,1) can be written in the iterative form as follows:
Thus,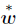 (1) in Eq. (21) can be approximated by
(1) in Eq. (21) can be approximated by 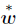 (q,1) ,where
Therefore,in the computation of
(q,1) ,where
Therefore,in the computation of 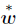 (q,1),once the inversion of A or the LU factorization of A is enough,the approximation of
(q,1),once the inversion of A or the LU factorization of A is enough,the approximation of 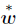 (q,1) to
(q,1) to 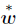 (1) has the accuracy of order O(|λi/λs+1|q+1). When
(1) has the accuracy of order O(|λi/λs+1|q+1). When 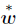 (1) is replaced by its qth-order approximation
(1) is replaced by its qth-order approximation 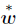 (q,1) ,the approximations of λ(2),c(1,i),and w(1) can be obtained by exactly the same way as described in Section 2. It is known from the analysis of Section 2 that w(2),the second-order derivative of the differentiable eigenvector w(0),can be expressed by Eq. (32),where
and
On the rightest side of Eq. (49),
Similarly,the calculation of
(q,1) ,the approximations of λ(2),c(1,i),and w(1) can be obtained by exactly the same way as described in Section 2. It is known from the analysis of Section 2 that w(2),the second-order derivative of the differentiable eigenvector w(0),can be expressed by Eq. (32),where
and
On the rightest side of Eq. (49),
Similarly,the calculation of 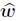 (q,2) can be written in the iterative form as follows:
Therefore,
(q,2) can be written in the iterative form as follows:
Therefore,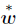 (2) in Eq. (32) can be approximated by
(2) in Eq. (32) can be approximated by 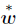 (q,2),where
When
(q,2),where
When 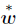 (2) is replaced by its qth-order approximation
(2) is replaced by its qth-order approximation 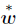 (q,2),the approximation of λ(3),c(2,i),and w(2) can be obtained by exactly the same way as described in Section 2. By the similar way,we can get the approximations of higher order eigenvalue and eigenvector derivatives.
4 Numerical examples
(q,2),the approximation of λ(3),c(2,i),and w(2) can be obtained by exactly the same way as described in Section 2. By the similar way,we can get the approximations of higher order eigenvalue and eigenvector derivatives.
4 Numerical examples 4.1 Numerical example for testing exact method
Consider a 3 × 3 matrix
The different eigenvalues of A are λ1 = 1 and λ2 = −1,whose multiplicities are,respectively,2 and 1,and whose corresponding eigenvectors and left eigenvectors of A are Thus,After perturbation by small parameter ε,A becomes
The eigenvalues of A(ε) are
Now,we investigate the derivatives of repeated eigenvalues and their corresponding differentiable eigenvectors of A after A is perturbed. The eigenvectors associated with λ1,1(ε) and λ1,2(ε) are
The first-,second-,and third-order derivatives of the eigenvalue λ1,1(ε) at ε = 0 are,respectively,1,0,and -1,and the first-,second-,and third-order derivatives of the eigenvalue λ1,2(ε) at ε = 0 are,respectively,-1,0,and 1. The eigenvector w(0,1)(ε) and its first- and second-order derivatives at ε = 0 are
The eigenvector w(0,2)(ε) and its first- and second-order derivatives at ε = 0 areCompared with the above exact results,the calculated results obtained by our exact method and by MATLAB programming have at least same 16 significant digits,which shows the correctness of our exact method. 4.2 Numerical example for testing approximate method
Consider an 8 × 8 matrix
The different eigenvalues of A are whose multiplicities are 1,2,2,2,and 1,respectively. The corresponding eigenvector sets of A are The corresponding left eigenvector sets of A are A(ε),the perturbed matrix of A,isNow,we investigate the efficiency of the approximate method for the eigensensitivity analysis associated with the repeated eigenvalue λ2. In this example,we take s= 3,i.e.,only the eigenpairs associated with the eigenvalues λ1,λ2,and λ3 of A are used. Associated with the differentiable eigenvectors w(0,1) and w(0,2),Table 1 and Table 2,respectively,give the relative errors of the second- and third-order eigenvalue derivatives and the first- and secondorder eigenvector derivatives by the qth-order (q= 1,2,3,4,5) approximate method,where the vector errors are in the maximal norm. The lower order derivatives used in the computation of the approximate values of the higher order derivatives are taken their exact values. It can be seen that the errors of the eigenvalue and eigenvector derivatives obtained by the qth-order approximate method are proportional to |λ2/λ4|q+1,which show the validity of the approximate method. It should be noted that if the lower order derivatives used in the computation of the approximate values of the higher order derivatives are taken their approximate values,then the accuracies of the computed approximate values of the higher order derivatives will be reduced.
 |
 |
An improved modal truncation method with arbitrarily high order accuracy is developed for calculating the second- and third-order eigenvalue derivatives and the first- and secondorder eigenvector derivatives of an asymmetric and non-defective matrix with repeated eigenvalues. The numerical example shows the validity of the method. If the different eigenvalues λ1,λ2,···,λr of the matrix satisfy |λ1|≤···≤|λr| and |λs|/|λs+1| < 1 for s ≤r-1 and if the method only uses the eigenparis corresponding to the eigenvalues λ1,λ2,···,λs,then associated with λi (i≤s) the errors of the eigenvalue and eigenvector derivatives obtained by the qth-order approximate method are proportional to |λi/λs+1|q+1. The method can easily be extended to the evaluation of higher order eigenvalue and eigenvector derivatives.
| [1] | Zhao, Y. Q., Liu, Z. S., Chen, S. H., and Zhang, G. Y. An accurate modal truncation method foreigenvector derivatives. Computers & Structures, 73(6), 609–614 (1999) |
| [2] | Nelson, R. B. Simplified calculation of eigenvector derivatives. AIAA Journal, 14(9), 1201–1205(1976) |
| [3] | Ojalvo, I. U. Efficient computation of modal sensitivities for systems with repeated frequencies.AIAA Journal, 26(3), 361–366 (1988) |
| [4] | Mills-Curran, W. C. Calculation of eigenvector derivatives for structures with repeated eigenvalues.AIAA Journal, 26(7), 867–871 (1988) |
| [5] | Dailey, R. L. Eigenvector derivatives with repeated eigenvalues. AIAA Journal, 27(4), 486–491(1989) |
| [6] | Friswell, M. I. Calculation of 2nd-order and higher-order eigenvector derivatives. Journal ofGuidance, Control and Dynamics, 18(4), 919–921 (1995) |
| [7] | Friswell, M. I. The derivatives of repeated eigenvalues and their associated eigenvectors. Journalof Vibration and Acoustics-Transactions of the ASME, 118(3), 390–397 (1996) |
| [8] | Lee, I. W., Jung, G. H., and Lee, J. W. Numerical method for sensitivity analysis of eigensystemswith non-repeated and repeated eigenvalues. Journal of Sound and Vibration, 195(1), 17–32 (1996) |
| [9] | Lee, I. W. and Jung, G. H. An efficient algebraic method for the computation of natural frequencyand mode shape sensitivities, 1: distinct natural frequencies. Computers & Structures, 62(3), 429–435 (1997) |
| [10] | Lee, I. W. and Jung, G. H. An efficient algebraic method for the computation of natural frequencyand mode shape sensitivities, 2: multiple natural frequencies. Computers & Structures, 62(3),437–443 (1997) |
| [11] | Wei, F. S. and Zhang, D. W. Eigenvector derivatives with repeated eigenvalues using generalizedinverse technique. AIAA Journal, 34(10), 2206–2209 (1996) |
| [12] | Lee, I.W., Kim, D. O., and Jung, G. H. Natural frequency and mode shape sensitivities of dampedsystems: part I, distinct natural frequencies. Journal of Sound and Vibration, 223(3), 399–412(1999) |
| [13] | Lee, I.W., Kim, D. O., and Jung, G. H. Natural frequency and mode shape sensitivities of dampedsystems: part II, multiple natural frequencies. Journal of Sound and Vibration, 223(3), 413–424(1999) |
| [14] | Choi, K. M., Jo, H. K., Kim, W. H., and Lee, I. W. Sensitivity analysis of non-conservativeeigensystems. Journal of Sound and Vibration, 274(3-5), 997–1011 (2004) |
| [15] | Choi, K. M., Cho, S. W., Ko, M. G., and Lee, I. W. Higher order eigensensitivity analysis ofdamped systems with repeated eigenvalues. Computers & Structures, 82(1), 63–69 (2004) |
| [16] | Liu, J. K. Universal perturbation technique for reanalysis of non-self-adjoint systems. AIAA Journal, 38(6), 1035–1039 (2000) |
| [17] | Adhikari, S. and Friswell, M. I. Calculation of eigensolution derivatives for nonviscously dampedsystems using Nelson’s method. AIAA Journal, 44(8), 1799–1806 (2006) |
| [18] | Najeh, G., Hichem, S., and Mnaouar, C. A direct algebraic method for eigensolution sensitivitycomputation of damped asymmetric systems. International Journal for Numerical Methods inEngineering, 68(6), 674–689 (2006) |
| [19] | Najeh, G., Mnaouar, C., and Hichem, S. Second-order eigensensitivity analysis of asymmetricdamped systems using Nelson’s method. Journal of Sound and Vibration, 300(3-5), 974–992(2007) |
| [20] | Xu, Z. H., Zhong, H. X., Zhu, X. W., and Wu, B. S. An efficient algebraic method for computingeigensolution sensitivity of asymmetric damped systems. Journal of Sound and Vibration, 327(3-5), 584–592 (2009) |
| [21] | Luongo, A. Eigensolutions sensitivity for nonsymmetric matrices with repeated eigenvalues. AIAAJournal, 31(7), 1321–1328 (1993) |
| [22] | Zhang, Z. Y. and Zhang, H. S. Eigensensitivity analysis of a defective matrix. AIAA Journal,39(3), 473–479 (2001) |
| [23] | Zhang, Z. Y. and Zhang, H. S. Higher-order eigensensitivity analysis of a defective matrix. AIAAJournal, 40(4), 751–757 (2002) |
| [24] | Zhang, Z. Y. and Zhang, H. S. Eigensensitivity analysis of defective matrix with zero first-ordereigenvalue derivatives. AIAA Journal, 42(1), 114–123 (2004) |
| [25] | Fox, R. L. and Kapoor, M. P. Rates of change eigenvalues and eigenvectors. AIAA Journal, 6(12),2426–2429 (1968) |
| [26] | Murthy, D. V. and Haftka, R. T. Derivatives of eigenvalues and eigenvectors of a general complexmatrix. International Journal for Numerical Methods in Engineering, 26(2), 293–311 (1998) |
| [27] | Juang, J. N., Ghaemmaghami, P., and Lim, K. B. Eigenvalue and eigenvector derivatives of anondefective matrix. Journal of Guidance, Control and Dynamics, 12(4), 480–486 (1989) |
| [28] | Bernard, M. L. and Bronowicki, A. J. Modal expansion method for eigensensitivity with repeatedroots. AIAA Journal, 32(7), 1500–1506 (1994) |
| [29] | Zhang, D. W. and Wei, F. S. Computation of eigenvector derivatives with repeated eigenvaluesusing a complete modal space. AIAA Journal, 33(9), 1749–1753 (1995) |
| [30] | Adhikari, S. and Friswell, M. I. Eigenderivative analysis of asymmetric non-conservative systems.International Journal for Numerical Methods in Engineering, 51(6), 709–733 (2001) |
| [31] | Adhikari, S. Derivative of eigensolutions of nonviscously damped linear systems. AIAA Journal,30(10), 2061–2069 (2002) |
| [32] | Zhang, Z. Y. and Zhang, H. S. Calculation of eigenvalue and eigenvector derivatives of a defectivematrix. Applied Mathematics and Computation, 176(1), 7–26 (2006) |
| [33] | Zhang, Z. Y. A development of modal expansion method for eigensensitivity analysis of a defectivematrix. Applied Mathematics and Computation, 188(2), 1995–2019 (2007) |
| [34] | Wang, B. P. Improved approximate methods for computing eigenvector derivatives in structuraldynamics. AIAA Journal, 29(6), 1018–1020 (1991) |
| [35] | Zeng, Q. H. Highly accurate modal method for calculating eigenvector derivatives in viscousdamping systems. AIAA Journal, 33(4), 746–751 (1995) |
| [36] | Kim, Y., Lee, S., and Junkins, J. L. Eigenvector derivatives for mechanical 2nd-order systems.Journal of Guidance, Control and Dynamics, 18(4), 899–906 (1995) |
| [37] | Moon, Y. J., Kim, B. W., Ko, M. G., and Lee, I. W. Modified modal methods for calculatingeigenpair sensitivity of asymmetric damped system. International Journal for Numerical Methodsin Engineering, 66(11), 1847–1860 (2004) |
 2013, Vol. 35
2013, Vol. 35








































































