Shanghai University
Article Information
- A. ALSAEDI, N. ALI, D. TRIPATHI, T. HAYAT. 2014.
- Peristaltic flow of couple stress fluid through uniform porous medium
- Appl. Math. Mech. -Engl. Ed., 35(4): 469-480
- http://dx.doi.org/10.1007/s10483-014-1805-8
Article History
- Received 2013-02-13;
- in final form 2013-08-15
2. Department of Mathematics & Statistics International Islamic University, Islamabad 44000, Pakistan;
3. Department of Applied Mathematics, IT-BHU, Varanasi 221005, India;
4. Department of Mathematics, Quaid-i-Azam University, Islamabad 44000, Pakistan
The flow of physiological fluids through vessels is a well documented problem of peristalticmotion. The movement of food bolus through oesophagus,chyme movement,flow of urine inureters and blood flow through vessels such as arteries,veins,arterioles,venules,and capillar-ies are some important examples of peristaltic flow. Latham[1],in his thesis,initiated studyof the peristaltic motion experimentally. Shapiro et al.[2] employed long wavelength and lowReynolds number. Both the cases of planar and axisymmetric flows were considered by them.The mechanical efficiency of the peristaltic pump and phenomena of trapping and reflux werediscussed. However,this investigation was related to viscous fluids. Therefore,it was not appli-cable to peristaltic flow of non-Newtonian fluids. Keeping this fact in mind,several researchersstudied the peristaltic flow of non-Newtonian fluids under various assumptions[3, 4, 5, 6, 7, 8, 9, 10].
It is well established fact that the classical Navier-Stokes theory is not adequate to describe the mechanics of fluids having high molecular weights like liquid crystals,polymeric solutions blood,etc. As a consequence of this inadequacy,many theories of micro-continua were developed by the researchers. The key feature of micro-continua theories is that they consider the continuous media as a set of structured particles which in addition to mass and velocity also have a substructure. It is assumed that this substructure is associated with the size of the particle,a moment of inertia density,and the micro-deformation tensor. The theory of micro-continua proposed by Stokes[11] accounts the particle size effects. In fact,Stokes theory is an extended version of the Navier-Stokes theory. This theory accounts for polar effects such as presence of anti-symmetric stress tensor,couple stresses,and body couples. Some recent investigations dealing with the peristaltic flow of a couple stress fluid in various configurations can be found in Refs.[12, 13, 14, 15, 16]. In these studies,the objective is to discuss the combined effects of the magnetic field and couple stress parameter on various features of peristaltic motion.
A medium containing tiny holes distributed throughout the matter is called a porousmedium. The involvement of parallel flow of fluids having different viscosity and density through a porous medium is extensively found in many technical processes. Particularly,parallel flows can be found in the chemical industry,in the packed bed reactors,in the petroleum industry,and many other processes. Natural examples of flow through porous media include filtration of fluids,water seepage in the bed of river,underground movement of water and oil,limestone,wood,etc. Physiological examples of flow through porous medium are human lung,bile duct,gall bladder with stones,and small blood vessels. It is known to us that localized narrowing is commonly found in arterial systems of humans or animals. The primarily cause of these narrowing developed in the arteries is intravascular plaques. The flow measurement through these narrow arteries is very helpful in the investigation of cardiovascular disease,particularly,atherosclerosis. The lumen of the coronary artery which is composition of fatty cholesterol and artery clogging blood clots can be regarded as a porous medium under some pathological con- ditions. Motivated by such facts,many researchers[17−30] studied the peristaltic flow of viscous fluid through a porous medium in symmetric/asymmetric channel and tube with the objective analyze permeability parameter on the flow quantities of interest. The above investigations en- compass constant and variable viscosity cases,couple stress fluid,generalized Newtonian fluid,micropolar fluid,and Maxwell fluid.
In this investigation,we consider the flow through a channel filled with the porous medium induced by traveling sinusoidal waves along the channel boundaries. An incompressible couple stress fluid is considered. The flow is analyzed subject to long wavelength and low Reynolds number. The effects of couple stress and permeability parameters on the peristaltic flow are analyzed. Graphs for pertinent parameters are displayed and discussed. 2 Mathematical model
We analyze the peristaltic flow of couple stress fluid filling the porous space. The fluid fills a symmetric channel of width 2a. Sinusoidal waves of constant speed c propagate along the channel boundaries. The align of wall surface is given by
where a is the half width of channel,b is the amplitude,λ is the wavelength,c is the wave speed,and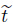 is the time.
is the time.
In absence of body forces and the body couples,the laws of mass and momentum conservation for flow of a couple stress fluid through the porous medium in the fixed frame yield the following aligns:
In the above aligns ρ,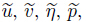 μ,μ1,and
μ,μ1,and 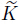 denote the fluid density,the axial velocity,the transverse velocity,the transverse coordinate,the pressure,the viscosity,the constant associated with the couple stress,the permeability parameter,respectively,and
Equations(2)-(4) can be put in the dimensionless form with the help of parameters defined as
where δ,φ,Re,and α are the wave number,the amplitude ratio,the Reynolds number,the couple stress parameter,respectively. In view of the long wavelength and low Reynolds number approximations,Eqs. (2)-(4) in the non-dimensional form read as
Equations (7),(9),and (10) yield
where
and
denote the fluid density,the axial velocity,the transverse velocity,the transverse coordinate,the pressure,the viscosity,the constant associated with the couple stress,the permeability parameter,respectively,and
Equations(2)-(4) can be put in the dimensionless form with the help of parameters defined as
where δ,φ,Re,and α are the wave number,the amplitude ratio,the Reynolds number,the couple stress parameter,respectively. In view of the long wavelength and low Reynolds number approximations,Eqs. (2)-(4) in the non-dimensional form read as
Equations (7),(9),and (10) yield
where
and
The volume flow rate is defined by
With Eq. (11) in Eq. (15),one has The wave frame (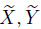 ) moving with the speed c and the fixed frame
) moving with the speed c and the fixed frame 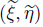 are related through the transformations
in which (
are related through the transformations
in which (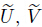 ) and
) and 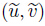 are the velocity components in the wave and fixed frames,respec- tively.
are the velocity components in the wave and fixed frames,respec- tively.
The volume flow rate in the fixed frame is
in which The averaging volume flow rate over one time period is From Eqs. (19) and (20),one has Through Eqs. (16) and (21),we have where The expressions of the pressure rise △p and the frictional force F over one wavelength are given by Using the definition of the maximum averaged flow rate and utilizing Eqs. (22) and (24),we get Equations (6)-(8) in the wave frame of reference can be written as By defining the stream function by the relations Eq. (27) is identically satisfied,and Eqs. (28) and (29) become Differentiating Eq. (31) with respect to η and using Eq. (32),we get The boundary conditions (9) and (10) become The two additional boundary conditions can be obtained by prescribing the value of stream function at the centerline and boundary[2],i.e., Equation (33) along with boundary conditions (34)-(36) is solved exactly to obtain the stream function. Later,the trapping phenomenon is discussed by using the obtained stream function. The explicit expression of stream function is given byWe note that in the wave frame,the corresponding problem and results are reduced to the results in Ref. [2] when α →∞ and K → ∞
In the following,we discuss the mechanical efficiency.
The ratio of the average rate per wavelength is done by the moving fluid against a pressure head,and the average rate at which the walls do work on the fluid is known as the mechanical efficiency[2]. Mathematically,we have
where
3 Numerical results and discussion
This section aims to discuss how the different emerging variable affects the fundamental features of peristaltic motion such as pressure rise over one wavelength,friction force across one wavelength,mechanical efficiency,and trapping. The region in which △p > 0,Q > 0 is known as the peristaltic pumping region. In this region,the peristaltic wave overcomes the pressure rise and drives the fluid in the direction of its propagation. When △p = 0,then fluid is solely propelled by the peristaltic wave. In the copumping region,where △p < 0,Q > 0,the pressure augments the flow due to peristalsis. Figures 1-3 illustrate the influence of couple stress parameter (α),permeability parameter (K),and amplitude ratio (Φ) on pressure rise over one wavelength (△p).
 |
| Fig. 1 Pressure difference across one wave-length vs. averaged flow rate for different values of α at Φ= 0.6 and K = 0.1 |
 |
| Fig. 2 Pressure difference across one wavelength vs. averaged flow rate for different values of K at Φ= 0.6 and α= 10.0 |
 |
| Fig. 3 Pressure difference across one wavelength vs. averaged flow rate for different values of Φ at K = 0.1 and α = 10.0 |
It is observed from Fig. 1 that pumping rate (Q) decreases with α in the peristaltic pumping and free pumping regions. Since large values of α correspond to the viscous fluid,therefore,we may conclude that for a couple stress,fluid peristalsis has to work as a positive displacement pump against greater pressure rise in comparison with viscous fluid. Physically,the parameter α is a measure of size of suspended fluid particles in the fluid. Small values of α correspond to the suspended particles in the fluid with large size. However,large values of α correspond to the clear fluid,i.e.,a fluid which is free of suspended particles. Thus,it seems physically acceptable that more effort is needed to pump a fluid with suspended particles in comparison with the clear fluid.
Figure 2 demonstrates that effects of K on Q in the peristaltic pumping region are similar to the effects of α,when △p >△pc. This is because of the fact that small values of the permeability parameter K imply that the radius of the holes distributed in the porous matrix is small. Therefore,resistance to the flow is large and hence pressure rise per wavelength △p is large. When △p < △pc,Q increases by increasing K. The value of △pc in Fig. 2 equals 3. Obviously,the value of △pcc depends on α and Φ. Similarly,in the free pumping region,increasing K increases the pumping rate.
The effects of Φon Q are displayed in Fig. 3. It is observed from this figure that increasing Φ increases the pumping rate Q in all the three cases,i.e.,when △p is positive,zero,or negative.
The effects of α,K,and Φ on friction force across one wavelength on the wall of channel (F) can be viewed with the help of Figs. 4-6. Physically,F represents the value of shear stress across one wavelength at the wall. These figures show that frictional force has reverse behavior in comparison to the pressure rise. We further note that there exists a critical value of the flow rate Q below (above) which the frictional force resists (assists) the flow. This critical value of Q decreases when the parameters α and K are increased. However,increasing Φ increases this critical value. Moreover,the resistance provided by F is larger for a couple stress fluid in comparison with the clear viscous fluid.
 |
| Fig. 4 Frictional force across one wavelength vs. averaged flow rate for different values of α at Φ = 0.6 and K = 0.1 |
 |
| Fig. 5 Frictional force across one wavelength vs. averaged flow rate for different values of K at Φ= 0.6 and α = 10.0 |
 |
| Fig. 6 Frictional force across one wavelength vs. averaged flow rate for different values of Φ at K = 0.1 and α = 10.0 |
Figures 7-9 show how the mechanical efficiency of the peristaltic pump (E) is affected by the parameters α,K,and Φ. We can see that nature of variation of E with respect to Q/Q0 is parabolic. Further,E decreases with α and K while it increases with Φ.
 |
| Fig. 7 Mechanical efficiency vs. ratio of averaged flow rate and maximum averaged flow rate for different values of α at Φ = 0.6 and K = 0.1 |
 |
| Fig. 8 Mechanical efficiency vs. ratio of averaged flow rate and maximum averaged flow rate for different values of K at Φ = 0.6 and α = 10.0 |
 |
| Fig. 9 Mechanical efficiency vs. ratio of averaged flow rate and maximum averaged flow rate for different values of Φ at K = 0.1 and α = 10.0 |
The variation of α and K on trapping phenomenon can be visualized with the aid of Figs. 10- 11. We choose a value of Q for which trapping is about the center streamline. The size of this trapped bolus decreases with α. This is perhaps due to the fact that the presence of suspended particles increase the volume of the bolus. However,it increases when large values of permeability parameter are accounted. Quite likely this observation is reflection of the fact that trapping phenomenon is more likely in a non-porous region.
 |
| Fig. 10 Streamlines in wave frame for different values of α when Q = 0.6,Φ = 0.6,and K = 5.0 |
 |
| Fig. 11 Streamlines in wave frame for different values of K when Φ = 0.6,Φ = 0.6,and α = 5.0 |
The peristaltic flow of couple stress fluid is studied in a planar channel. The medium in- side the channel is considered as the porous. Closed form solutions of axial velocity and axial pressure gradient are obtained. The stream function formulation is utilized in the wave frame. A parametric study is carried out in order to analyze the effects of various parameters on the salient features of peristaltic motion. It is revealed that the presence of porous medium gives rise to a critical value of △p,i.e.,△pc in the peristaltic pumping region. Above this critical value,the peristaltic pumping rate decreases by increasing K for a fixed △p,and below this value,the situation is reversed. Further,the mechanical efficiency of peristaltic pump decreases by increasing K. Moreover,the presence of porous medium affects the trapping phenomenon in the sense that volume of the trapped bolus increases and it circulates faster when the per- meability parameter is increased.
| [1] | Latham, T. W. Fluid Motion in a Peristaltic Pump, M. Sc. dissertation, Massachusetts Instituteof Technology (1966) |
| [2] | Shapiro, A. H., Jafferin, M. Y., and Weinberg, S. L. Peristaltic pumping with long wavelengths atlow Reynolds number. Journal of Fluid Mechanics, 35, 669–675 (1969) |
| [3] | Mekheimer, K. S., El-Shehawey, E. F., and Alaw, A. M. Peristaltic motion of a particle fluidsuspension in a planar channel. International Journal of Theoretical Physics, 37, 2895–2920 (1998) |
| [4] | Hayat, T. and Ali, N. Peristaltically induced motion of a MHD third grade fluid in a deformabletube. Physica A, 370, 225–239 (2006) |
| [5] | Hayat, T. and Ali, N. On mechanism of peristaltic flows for power-law fluids. Physica A, 371,188–194 (2006) |
| [6] | Pandey, S. K. and Tripathi, D. Unsteady peristaltic transport of Maxwell fluid through finitelength tube: application to oesophageal swallowing. Applied Mathematics and Mechanics (EnglishEdition), 33(1), 15–24 (2012) DOI 10.1007/s10483-012-1530-9 |
| [7] | Wang, Y., Hayat, T., and Hutter, K. Peristaltic flow of a Johnson-Segalman fluid through adeformable tube. Theoretical and Computational Fluid Dynamics, 21, 369–380 (2007) |
| [8] | Ali, N., Wang, Y., Hayat, T., and Oberlack, M. Long wavelength approximation to peristalticmotion of an Oldroyd 4—constant fluid in a planar channel. Biorheolgy, 45, 611–628 (2008) |
| [9] | Haroun, M. H. Effect of Deborah number and phase difference on peristaltic transport of a third-order fluid in an asymmetric channel. Communications in Nonlinear Science and Numerical Simulation, 12, 1464–1480 (2007) |
| [10] | Hayat, T., Noreen, S., and Alsaedi, A. Slip and induced magnetic field effects on peristaltic trans-port of Johnson-Segalman fluid. Applied Mathematics and Mechanics (English Edition), 33(8),1035–1048 (2012) DOI 10.1007/s10483-012-1603-6 |
| [11] | Stokes, V. K. Couple stress fluid. Physics of Fluids, 9, 1709–1715 (1966) |
| [12] | Srivastava, L. M. Peristaltic transport of a couple stress fluid. Rheologica Acta, 25, 638–641 (1986) |
| [13] | El-Shehawey, E. F. and Mekheimer, K. S. Couple stress in peristaltic transport of fluids. Journalof Physics D: Applied Physics, 27, 1163–1170 (1994) |
| [14] | El-Shehawey, E. F. and El-Sebaei, W. Couple stress in peristaltic transport of a magneto-fluid.Physica Scripta, 64, 401–409 (2001) |
| [15] | Mekheimer, Kh. S. Effect of the induced magnetic field on the peristaltic flow of a couple stressfluid. Physics Letters A, 372, 4271–4278 (2008) |
| [16] | Shobh, A. M. Interaction of couple stresses and slip flow on peristaltic transport in uniform andnon-uniform channels. Turkish Journal of Engineering and Environmental Sciences, 32, 117–123(2008) |
| [17] | Afifi, N. A. S. and Gad, N. S. Interaction of peristaltic flow with pulsatile magneto-fluid througha porous medium. Acta Mechanica, 149, 229–237 (2001) |
| [18] | Mekheimer, K. S. Nonlinear peristaltic transport through a porous medium in an inclined planarchannel. Journal of Porous Media, 6, 189–201 (2003) |
| [19] | Elsehawey, E. F., Sobh, A. M., and E-Elbarbary, E. M. Peristaltic motion of a generalized New-tonian fluid through a porous medium. Journal of Physical Society of Japan, 69, 401–407 (2000) |
| [20] | Elshehawey, E. F., Eldabe, N. T., Elghazy, E. M., and Ebaid, A. Peristaltic transport in anasymmetric channel through a porous medium. Applied Mathematics and Computation, 182, 140–150 (2006) |
| [21] | El-Shehawey, E. F. and Husseny, S. Z. A. Effects of porous boundaries on peristaltic transportthrough a porous medium. Acta Mechanica, 143, 165–177 (2000) |
| [22] | Hayat, T., Ali, N., and Asghar, S. Hall effects on peristaltic flow of a Maxwell fluid in a porousmedium. Physics Letters A, 363, 397–403 (2007) |
| [23] | Pandey, S. K. and Chaube, M. K. Peristaltic flow of a micropolar fluid through a porous medium inthe presence of an external magnetic field. Communications in Nonlinear Science and NumericalSimulation, 16, 3591–3601 (2011) |
| [24] | Mahmoud, S. R., Afifi, N. A. S., and Al-Isede, H. M. Effect of porous medium and magneticfield on peristaltic transport of a Jeffery fluid. International Journal of Mathematical Analysis, 5,1025–1034 (2011) |
| [25] | Hayat, T., Qureshi, M. U., and Hussain, Q. Effect of heat transfer on the peristaltic flow of anelectrically conducting fluid in a porous space. Applied Mathematical Modelling, 33, 1869–1873(2009) |
| [26] | El-Koumy, S. R., Barakat, E. S. I., and Abdesalam, S. I. Hall and porous boundaries effects onperistaltic transport through porous medium of Maxwell model. Transport in Porous Media, 94,643–658 (2012) |
| [27] | Srinivas, S. and Muthuraj, R. Effects of chemical reaction and space porosity on MHD mixedconvective flow in a vertical asymmetric channel with peristalsis. Mathematical and ComputerModelling, 54, 1213–1227 (2011) |
| [28] | Vajravelu, K., Sreenadh, S., and Lakshminarayana, P. The influence of heat transfer on peristaltictransport of a Jeffery fluid in a vertical porous stratum. Communications in Nonlinear Scienceand Numerical Simulation, 16, 3107–3125 (2011) |
| [29] | Abo-Aldahab, E., Barakat, E., and Nowar, K. Hall currents and heat transfer effects on peristaltictransport in a vertical asymmetric channel through a porous medium. Mathematical Problems inEngineering (2012) DOI 10.1155/2012/840203 |
| [30] | Lakshminarayana, P., Sreenadh, S., and Sucharitha, G. Peristaltic pumping of a conducting fluidin a channel with a porous peripheral layer. Advances in Applied Sciences Research, 3, 2890–2899(2012) |
 2013, Vol. 35
2013, Vol. 35






























