Shanghai University
Article Information
- FANG CHEN, QING-QUAN LIU. 2014.
- Modified asymptotic Adomian decomposition method for solving Boussinesq equation of groundwater flow
- Appl. Math. Mech. -Engl. Ed., 35(4): 481–488
- http://dx.doi.org/10.1007/s10483-014-1806-7
Article History
- Received 2013-09-13;
- in final form 2013-11-13
2. School of Applied Science, Beijing Information Science and Technology University, Beijing 100192, P. R. China
The Adomian decomposition method (ADM) was proposed by Adomian[1] in the beginning of the 1980s. The ADM is a simple and efficient method for solving the analytic approximant of the nonlinear equations. People deeply research it according to the basic principle and apply it to many fields of science and engineering. The convergence property,noise phenomenon,and various modifications of ADM have been studied. Though the principle of ADM is simple,and it can be used to solve many equations,ADMneeds to be modified for getting efficient approximate solution to the real-world problems. For example,based on the choice of initial term,two-step and multi-step ADMs were proposed[2, 3, 4]. An implicit determination of the initial term was studied by using the ADM[5]. Other modified ADMs for solving the nonlinear equations were discussed in Refs. [6, 7]. Based on the ADM and the modified ADM,the weighted ADM was proposed in Ref. [8]. The ADM can solve some special nonlinear equations by combining the Laplace transform and the Padé approximant[9, 10, 11, 12, 13].
Assume the equipotential line is vertical,the flow is horizontal,and the vertical component of seepage is ignored on the activities of the groundwater flow. Then the differential equations describing the groundwater flow can be formulated as follows,which is usually called the Boussinesq equation:
The Boussinesq equation was broad applied in groundwater dynamics. We do not take into account the replenishment of rainfall,that is,there is no recharge. At the same time,we neglect the effect of vertical flow in the aquifer and the capillary effects on the groundwater table,and only discuss the approximate solution of this Boussinesq equation. Though the Boussi- nesq equation is simple,the analytic solution is difficultly gotten under initial and boundary conditions. People have studied the Boussinesq equation in many cases[14, 15, 16, 17].
In this paper,based on the ADM,we give an modified asymptotic ADM. Then the modified asymptotic ADM is used to solve the Boussinesq equation,which describes the groundwater flow. From the example,we deserve that the growing of the time the solution given by the modified asymptotic ADM well approximates the exact solution. This shows the efficiency of the modified asymptotic ADM. 2 Basic principle of Adomian and modified ADMs 2.1 ADM
Adomian proposed the ADM in 1983,which was used to solve the approximate solution of the nonlinear differential equations. The basic idea is the principle of invertible operator. Usually,a nonlinear differential equation can be written as
where L is the highest-order derivative which is assumed to be easily invertible,R is a linear operator,N is a nonlinear operator,and g(t) is the source term.Let L−1 be the inverse operator of the linear operator L,which means that L−1 is an integration operator. The nonlinear differential equation (1) can be rewritten as
For example,if we define L = d2/dt2 to be the second order derivative operator,and L−1 = ∫t0 ∫t0 dtdt to be the 2-fold definite integration operator from 0 to t,then it holds thatThe solution u and the nonlinear term Nu are defined by the series
where In fact,An are the specially generated (Adomian) polynomials with respect to the specific nonlinearity. In essence,the series in An polynomials form the generalized Taylor series.Substituting the above notations into (2),we have
Therefore,we can define the components un by the following recursive relationship: Let Then,it holds that Hence,the n-term approximation ψn approaches u as n →∞.In applications,we can obtain the approximate solution from the regulation of the front terms. On the other hand,we can use only a few front terms to approximate the exact solution.
Theoretically,the ADM can yield an approximate solution to the differential equation with initial or/and boundary conditions. However,we suffer a lot of difficulties in practical appli- cations. Aiming at the Boussinesq equation,we introduce a modified asymptotic ADM in this paper. 2.2 Modified asymptotic ADM
The modified asymptotic ADM is the invertible case of the ADM,which refers to research the characteristic of solution about the grown time. The basic idea of the modified asymptotic ADM is still the principle of the ADM. Consider a class of nonlinear differential equations
where L is the highest-order derivative,R is a linear operator, is a derivative,N is a nonlinear operator,and g(t) is the source term.
is a derivative,N is a nonlinear operator,and g(t) is the source term.
Firstly,applying the inverse operator  −1 to both sides of the nonlinear differential equation(3),we have
−1 to both sides of the nonlinear differential equation(3),we have
We define the series of the solution u and the nonlinear term Nu,which are the same as those in the ADM,as follows:
Substituting the above expressions into the nonlinear differential equation (4),we have
Therefore,we obtain the following recursive relationship: From the above equations,we can obtain un (n = 0,1,2,· · · ) by direct computation. Finally, we have the approximate solution or the exact solution of u. 3 Approximate solution of Boussinesq equationThe groundwater flow without recharge can be described as the nonlinear Boussinesq equation[14, 15]. Consider the dimensionless Boussinesq equation as follows:
where h(x,t) is the hydraulic head,x is the dimensionless distance,t is the dimensionless time,h(0,t) is the left boundary condition,and h(x,0) is an initial condition across the aquifer. The above equation describes unstable and one dimensional groundwater flow without recharge. In this case,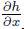 (3,t) = 0,which shows that the right boundary is impermeable. Hence,h(x,0) presents the hydraulic head at the initial time. This is a nonlinear differential equation (5) with
(3,t) = 0,which shows that the right boundary is impermeable. Hence,h(x,0) presents the hydraulic head at the initial time. This is a nonlinear differential equation (5) with
This is a nonlinear differential equation (5) with the initial condition (6) and the boundary conditions (7). Define
Then,the nonlinear differential equation (5) has the form Since the initial condition (6) is known,we let L−1t = ∫0t dt,and apply L−1t to both sides of the above equation. Then,we get Using the standard ADM,we get Thus,the approximate solution to h is given by Note that the approximate solution (8) satisfies the initial condition (6),but does not satisfy the boundary condition (7).The nonlinear differential equation (5) can be rewritten as
Let L−1xx = ∫0x∫0x dxdx,and apply L−1xx on both sides of the above equation. Then,we have Applying the modified asymptotic ADM,we obtain According to the boundary condition (7),the first term h0 is given by Since h0 is known,the expressions of h1 and h2 can be obtained from (9) as and In this case,the expression of h2 is complicated,so for the convenience we only use the first and the second terms to approximate the exact solution. The approximate solution satisfies Note that the approximate solution (10) satisfies the boundary condition (7),but does not satisfy the initial condition (6).In fact,the exact solution of the Boussinesq equation (5) under the initial and the boundary conditions[14] is
4 Comparisons and discussion between approximate and exact solutionsIn this section,we compare the approximate solutions by the ADM and by the modified asymptotic ADM with the exact solutions (see Figs. 1-2),respectively. Note that in these two figures we use different scalars in the longitudinal coordinates due to great different scalars in the solutions. From Fig. 1,we see that the approximate solution computed by the ADM (8) is much closer to the exact solution (11) at t = 1 than that computed by the modified asymptotic ADM (10). The approximate solution computed by the modified asymptotic ADM (10) is close to the exact solution (11) at t = 10 and t = 100,but the approximate solution computed by the ADM (8) is increasingly far away from the exact solution. Also,from Fig. 2,we see that the approximate solution computed by the modified asymptotic ADM (10) is close to the exact solution (11) at x = 1,x = 10 and x = 100,but the approximate solution computed by the ADM (8) is increasingly far away from the exact solution. For the Boussinesq equation (5),the modified asymptotic ADM yields more accurate approximate solution than the ADM when only two terms are used,and its approximate solution is also closer to the exact solution with the growing of the time.
 |
| Fig. 1 Water line changes with distance |
 |
| Fig. 2 Hydraulic head changes with time at different distances |
In fact,ADM is a flexible method. Though ADM can give an approximation solution for a general differential equation,but this approximation solution is not always the best. In recent years,for a specific equation,people give a new ADM by using the basic principle of the ADM. In theory,there is no concrete standard to compare and evaluate these methods. In the above,we give the modified asymptotic ADM for the Boussinesq equation (5),and illustrate that the modified aymptotic ADM is better than ADM by numerical examples. 5 Conclusions
For the Boussinesq equation which describes the groundwater flow without recharging,we propose the modified asymptotic ADM. Only using two terms,with this method we can compute a significantly approximate solution. From the examples we find that the approximate solution computed by the modified asymptotic ADM is much closer to the exact solution than that computed by the ADM. Moreover,with the growing of the time,at any point the approximate solution computed by the modified asymptotic ADM is close to the exact solution,but the approximate solution computed by the modified asymptotic ADM may be increasingly far away from the exact solution.
| [1] | Adomian, G. Stochastic Systems, Academic Press, New York (1983) |
| [2] | Luo, X. G. A two-step Adomian decomposition method. Applied Mathematics and Computation,170, 570–583 (2005) |
| [3] | Wazwaz, A. M. and El-Sayed, S. M. A new modification of the Adomian decomposition methodfor linear and nonlinear operators. Applied Mathematics and Computation, 122, 393–405 (2001) |
| [4] | Wazwaz, A. M. The modified decomposition method for analytic treatment of differential equa-tions. Applied Mathematics and Computation, 173, 165–176 (2006) |
| [5] | Jin, C. R. and Liu, M. Z. A new modification of Adomian decomposition method for solving akind of evolution equation. Applied Mathematics and Computation, 169, 953–962 (2005) |
| [6] | Naranmandula. Adomian’s asymptotic decomposition method and its applications in mechanicalproblems (in Chinese). College Physics, 22(8), 11–13 (2003) |
| [7] | Rach, R. and Duan, J. S. Near-field and far-field approximations by the Adomian and asymptoticdecomposition methods. Applied Mathematics and Computation, 217, 5910–5922 (2011) |
| [8] | Shidfar, A. and Garshasbi, M. A weighted algorithm based on Adomian decomposition methodfor solving an special class of evolution equations. Commun. Nonlinear Sci. Numer. Simulat., 14,1146–1151 (2009) |
| [9] | Jiao, Y. C., Yamamoto, Y., Dang, C., and Hao, Y. An aftertreatment technique for improving theaccuracy of Adomian’s decomposition method. Computers and Mathematics with Applications,43, 783–798 (2002) |
| [10] | Sivakumar, T. R. and Baiju, S. Shooting type Laplace-Adomian decomposition algorithm fornonlinear differential equations with boundary conditions at infinity. Applied Mathematics Letters,24, 1702–1708 (2011) |
| [11] | Venkatarangan, S. N. and Rajalakshmi, K. A modification of Adomian’s solution for nonlinearoscillatory systems. Computers and Mathematics with Applications, 29(6), 67–73 (1995) |
| [12] | Venkatarangan, S. N. and Rajalakshmi, K. Modification of Adomian’s decomposition method tosolve equations containing radicals. Computers and Mathematics with Applications, 29, 75–80(1995) |
| [13] | Wazwaz, A. M. The combined Laplace transform-Adomian decomposition method for handlingnonlinear Volterra integro-differential equations. Applied Mathematics and Computation, 216,1304–1309 (2010) |
| [14] | Polubarinova-Kochina, P. Y. Theory of Groundwater Movement (in Russian), Nauka, Moscow(1977) |
| [15] | Serrano, S. E. Modeling groundwater flow under transient nonlinear free surface. Journal of HydrologicEngineering, 8(3), 123–132 (2003) |
| [16] | Sun, J. P., Liu, Q. Q., Li, J. C., and An, Y. Effects of rainfall infiltration on deep slope failure.Science in China Series G: Physics Mechanics and Astronomy, 52(1), 108–114 (2009) |
| [17] | Sun, J. P., Li, J. C., Liu, Q. Q., and Zhang, H. Q. Approximate engineering solution for predictinggroundwater table variation during reservoir drawdown on the basis of the Boussinesq equation.Journal of Hydrologic Engineering, 16(10), 791–797 (2011) |
 2013, Vol. 35
2013, Vol. 35































