Shanghai University
Article Information
- S. NADEEM, S. T. HUSSAIN. 2014.
- Heat transfer analysis of Williamson fluid over exponentially stretching surface
- Appl. Math. Mech. -Engl. Ed., 35(4): 489–502
- http://dx.doi.org/10.1007/s10483-014-1807-6
Article History
- Received 2012-11-17;
- in final form 2013-11-18
In many practical situations,the stretching surface does not need to be linear,e.g.,in plasticsheet stretching. The heat transfer analysis of boundary layer flow over a continuous stretchingsurface with prescribed temperature or heat flux has gained considerable attention due to itsapplications in manufacturing processes of polymer sheets,glass fibre,paper production,metalwires,plastic films,etc. In polymer,the glass and plastic industry quality of the final productgreatly depends on the rate of cooling. Sakiadis[1] was the first to study the boundary layerflow over a continuous stretching surface. He developed the two dimensional boundary layerequations. Tsou et al.[2] examined the heat transfer effects on the boundary layer flow over astretching surface. Erickson et al.[3] extended this work for mass transfer by considering suctionand injection. Later on,many researchers have given their insight into boundary layer flowsover linear stretching surfaces[4, 5, 6].
Kumaran and Ramanaiah[7] considered the quadratic stretching on the viscous fluid flow over a stretching surface,and obtained the closed form solutions. Ali[8] considered power law stretching and temperature to investigate the thermal boundary layer. Elbashbeshy[9] discussed the flow and heat transfer of viscous fluid by considering the exponential stretching. Sanjayanand and Khan[10] extended this work for heat and mass transfer of viscoelastic fluid by considering the viscous dissipation and elastic deformation. Magyari and Keller[11] devel- oped the numerical solution for heat and mass transfer of viscous fluid over an exponentially stretching surface. Nadeem et al.[12] discussed the thermal radiation effects of Jeffery fluid over an exponentially stretching surface,and compared the homotopy analysis method (HAM) results with the numerical results obtained by Magyari and Keller[11]. More recently,Nadeem and Lee[13] studied the nano particle effects on the boundary layer flow of viscous fluid due to exponential stretching.
HAM is a popular technique among researchers[14, 15, 16, 17]. The optimal HAM (OHAM) is a refined and better version of HAM[14] . There are various types of OHAM,i.e.,basic OHAM,three parameter OHAM,finite parameter OHAM,and infinite parameter OHAM. All these types are discussed in detail by Liao[18]. We employ the basic OHAM to obtain the solution. In the basic OHAM,the squared residual error is minimized to obtain the optimized values of the convergence control parameters. Liao[19] presented the comparison of various OHAM approaches. He suggested that the basic OHAMand the three parameter OHAMare better than other OHAM approaches when compared in respect to the computational efficiency. Wang[20] used the three parameter OHAM to obtain the solution of the Kawahara equation. Nadjafi and Jafari[21] compared Liao’s OHAM with Niu’s one-step OHAM[22]. They used both techniques to obtain the solutions of linear Volterra integro-differential equations,and presented that Liao’s OHAM is more accurate to determine the convergence-control parameter. Fan and You[23] discussed in detail the global and step by step approaches to obtain the optimized convergence control parameter.
However,the flow of Williamson fluid over an exponentially stretching sheet has not been considered. In the present paper,we discuss the heat transfer analysis of pseudoplastic fluid over a porous exponentially stretching sheet with the help of the Williamson fluid model[24, 25, 26, 27, 28, 29]. The governing boundary layer equations are first simplified by using suitable similarity trans- formations. The resulting equations are solved analytically by OHAM for two cases,i.e.,pre- scribed exponential order surface temperature (PEST) and prescribed exponential order heat flux (PEHF). The convergence of the obtained solutions is examined with the help of average squared residual error tables. Graphs are plotted to observe the effects of theWilliamson param- eter,the suction/injection parameter,and the Prandtl number on the velocity and temperature profiles. Finally,tables are drawn for the skin friction and wall temperature gradient 2 Fluid model
For the Williamson fluid model,the Cauchy stress tensor S is defined as[29]
where Τ is the extra stress tensor,μ0 is the limiting viscosity at zero shear rate,μ∞ is the limiting viscosity at the infinite shear rate,Γ > 0 is a time constant,A1 is the first Rivlin-Erickson tensor,and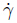 is defined as
Here,we consider the case for which
Then,we obtain
or
2.1 Mathematical formulation
is defined as
Here,we consider the case for which
Then,we obtain
or
2.1 Mathematical formulation
Let us consider a steady,two dimensional flow of an incompressible Williamson fluid over an exponentially stretching porous surface. The plate is exponentially stretched along the x-axis with a velocity Uw = Uo exp( ) at y = 0. Here,we assume the no slip boundary condition. The fluid near the wall has the velocity Uw and the temperature Tw. The stretched plate is also assumed to be porous. υ= −β(x) is the velocity on the wall. The schematic flow diagram is shown in Fig. 1. The governing boundary layer equations for flow and heat transfer in the absence of body force and viscous dissipation can be written as[30]
) at y = 0. Here,we assume the no slip boundary condition. The fluid near the wall has the velocity Uw and the temperature Tw. The stretched plate is also assumed to be porous. υ= −β(x) is the velocity on the wall. The schematic flow diagram is shown in Fig. 1. The governing boundary layer equations for flow and heat transfer in the absence of body force and viscous dissipation can be written as[30]
 |
| Fig. 1 Schematic diagram of boundary layer flow over stretching sheet |
The boundary conditions for the above mentioned cases are
For both cases, Introduce the following transformations in Eqs. (7)-(9): For the PEST case, For the PEHF case,After using the above transformations,our governing equations with the corresponding boundary equations take the following forms:
where s is the suction/injection parameter (s < 0 for suction and s > 0 for injection),and λ is the dimensionless Williamson parameter defined asFor λ = 0,Eq. (16) reduces to the classical boundary layer equation for viscous flow. Physical quantities of interest are the coefficient of the skin friction cf and the wall temperature gradient θ′(0). After using the boundary layer approximations,τw is given by
The coefficient of skin friction is defined as
In the dimensionless form,the skin friction becomes where Re =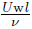 is the Reynolds number.
3 Homotopy analysis solutions
is the Reynolds number.
3 Homotopy analysis solutionsHAM is a strong analytic technique to solve linear and non-linear,ordinary and partial differential equations. HAM was developed by Liao in 1992. This technique unified several previous techniques like the Adomian decomposition method,the δ-expansion method,and the Lyapunov artificial small parameter method. HAM can be equally applied to weak and strong non-linear problems because it is independent of small/large physical parameter restriction. It also provides a way to check and adjust the convergence of the obtained solution with the help of auxiliary parameters and base functions. We choose the set of base functions
Then,we can write where am,nk,bm,nk,and cm,nk are the coefficients. With the help of the boundary conditions defined in Eqs. (16)-(18),the initial approximation and the auxiliary linear operator are chosen as where Ci (i= 1,2,· · · ,7) are the arbitrary constants. 3.1 Deformation equationsIf q ∈[0, 1] is the embedding parameter and the non-zero auxiliary parameter is h,then the problem at the zeroth-order deformation is given by
where the nonlinear operators are defined as When q = 0 and q = 1,we have With the help of Taylor series expansion,we can write The auxiliary parameter h is chosen in such a way that Eq. (31) converges at q = 1. Thus,The mth-order approximation is defined as
where The general solution to Eq. (34) is defined as where fm*(η),θm*(η),and Φm*(η) are special functions. We can determine the constants by using Eq. (35) as follows:The solution is obtained with the help of OHAM[18]. We can calculate any order approxi- mation for m = 1,2,3,· · · with the help of Mathematica. 3.2 Optimal values of convergence parameters
It is noteworthy that our solutions f(η),θ(η),and Φ(η) contain unknown convergence control (auxiliary) parameters (hf ,hθ,hΦ). To find out the optimal values of the convergence control parameters,we define the exact squared residuals at the mth-order approximation as follows:
and where εmt and εms are the total squared residual errors at the mth-iteration for the PEST case and the PEHF case,respectively. It is obvious that more quickly εmt and εms approach to zero,faster the corresponding solutions converge. Thus,at the mth-iteration,the optimal values of convergence control parameters are given by the minimums of εmt and εms,corresponding to the set of these equationsThe total squared residual error defined by Eq. (41) takes too much CPU time to calculate the error even if the order of approximation is not very high. Thus,to increase the computational efficiency,we define the discrete squared residual error (as defined by Liao[19]) at the mth- iteration by
where The total discrete squared residual errors are defined as In the present paper,the total discrete squared residual error is used to obtain the optimal convergence control parameters. In order to obtain the local optimal convergence control parameters,we directly employ the minimize command in the computational software Mathematica. 4 Results and discussionWe use the basic OHAM to obtain the results and the discrete squared residual error approach to obtain the optimal values of the convergence control parameters when
Tables 1 and 2 are drawn to get the local optimal convergence control parameters at different orders of approximation for PEST and PEHF cases,respectively. For both cases,it is found that the total discrete squared residual error decreases with the number of iterations. Tables 3 and 4 show the average squared residual errors for velocity and temperature equations cor- responding to the set of optimal values obtained in Tables 1 and 2,respectively. It is very clear that the average squared residual errors and total squared residual errors decrease as the order of approximation increases,which assures that the solution is convergent at higher order approximations. The results will be similar if we choose the values of the optimal convergence parameters from any higher order approximation. We choose the 8th iteration set of optimal values to plot figures and draw tables in the coming sections. |
 |
 |
 |
Since the momentum equation is decoupled from heat equation,the velocity profile is not affected by the choice whether the PEST or PEHF case. Figures 2 and 3 are drawn to observe the impact of the Williamson and suction/injection parameters on the velocity. It is observed that the velocity profile and momentum boundary layer thickness decrease with the increases in the Williamson parameter and the suction parameter (i.e.,negative increase in s) while increase for the case of injection (i.e.,positive increase in s),which is justified by the fact that as the fluid is injected to the stretching surface,it covers the region near the wall which causes an increase in the momentum boundary layer thickness. For the case of suction,the fluid moves out from the region closed to the wall,making it difficult for the boundary layer to establish. Thus,the net effect of suction is to slow down the flow and decrease the boundary layer.
 |
| Fig. 2 Velocity profile for different λ |
 |
| Fig. 3 Velocity profile for different s |
In both PEST and PEHF cases,the temperature profile and thermal boundary layer thick- ness increase with the increases in the Williamson parameter and the injection parameter while decrease with the increase in the suction parameter (see Figs. 4-7). It is also observed that the temperature profile and the thermal boundary layer thickness decrease with the increase in the Prandtl number for both cases,which is consistent with the fact that in heat flow problems,the Prandtl number controls the relative thickness of the momentum and thermal boundary layers.
 |
| Fig. 4 Temperature profile in PEST case for different λ |
 |
| Fig. 5 Temperature profile in PEST case for different s |
 |
| Fig. 6 Temperature profile in PEHF case for different λ |
 |
| Fig. 7 Temperature profile in PEHF case for different s |
Figures 8 and 9 show the temperature profiles in PEST and PEHF cases for different Pr. It can be seen from Figs. 8 and 9 that the heat diffuses very quickly for small values of the Prandtl number.
 |
| Fig. 8 Temperature profile in PEST case for different Pr |
 |
| Fig. 9 Temperature profile in PEHF case for different Pr |
Tables 5-7 are drawn to observe the effects of the effective parameters on the skin friction and wall temperature gradient. Since the skin friction is given by - ,where viscosity appears in the denominator of the Reynolds number,it decreases with the increase in the non- Newtonian Williamson parameter. Mathematically,from Eq. (22),we can see that the skin friction is the sum of f"(0) and its square. Since f"(0) is negative while its square is positive which is multiplied by a fraction (λ) less than 1,the difference of them reduces as we increase λ. Thus,the skin friction decreases with the increase in λ,as appeared in Table 5. It is also noticed that the skin friction decreases with the increase in the suction/injection parameter s. From Table 6,it is observed that the wall temperature gradient decreases with the increases in the Williamson and suction/injection parameters. The wall temperature gradient increases with the increase in the suction parameter because suction causes heat drain which resultantly increases the temperature gradient. Therefore,suction can be used to control the temperature of a process. Since the fluid is injected through wall,the wall temperature gradient decreases for the case of injection. Table 7 shows that the wall temperature gradient increases with the increase in the Prandtl number. Tables 6 and 7 are drawn only for the PEST case because for the PEHF case,we have Φ′(0) = -1.
,where viscosity appears in the denominator of the Reynolds number,it decreases with the increase in the non- Newtonian Williamson parameter. Mathematically,from Eq. (22),we can see that the skin friction is the sum of f"(0) and its square. Since f"(0) is negative while its square is positive which is multiplied by a fraction (λ) less than 1,the difference of them reduces as we increase λ. Thus,the skin friction decreases with the increase in λ,as appeared in Table 5. It is also noticed that the skin friction decreases with the increase in the suction/injection parameter s. From Table 6,it is observed that the wall temperature gradient decreases with the increases in the Williamson and suction/injection parameters. The wall temperature gradient increases with the increase in the suction parameter because suction causes heat drain which resultantly increases the temperature gradient. Therefore,suction can be used to control the temperature of a process. Since the fluid is injected through wall,the wall temperature gradient decreases for the case of injection. Table 7 shows that the wall temperature gradient increases with the increase in the Prandtl number. Tables 6 and 7 are drawn only for the PEST case because for the PEHF case,we have Φ′(0) = -1.
 |
 |
In the present paper,we analyze the heat transfer effects on the boundary layer flow of Williamson fluid over an exponentially stretching surface for two special cases,i.e.,PEST and PEHF. It is found that OHAM can be successfully employed to solve the coupled system of non-linear differential equations. The important findings are concluded as follows:
(i) The velocity and momentum boundary layer decrease with the increases in theWilliamson parameter and the suction parameter while increase with the increase in the injection parameter.
(ii) Both the PEST case and the PEHF case have qualitatively the same results. For both cases,the temperature and thermal boundary layer decrease with the increase in the Prandtl number.
(iii) The skin friction decreases with the increase in the Williamson parameter λ.
(iv) The wall temperature gradient decreases with the increases in the Williamson and suction/injection parameters and increases with the increase in the Prandtl number.
(v) Suction can be used as a mean to the regulate temperature of a process.
| [1] | Sakiadis, B. C. Boundary layer behavior on continuous solid flat surfaces. American Institute ofChemical Engineers Journal, 7, 26–28 (1961) |
| [2] | Tsou, F. K., Sparrow, E. M., and Goldstein, R. J. Flow and heat transfer in the boundary layeron a continuous moving surface. International Journal of Heat and Mass Transfer, 10, 219–235(1967) |
| [3] | Erickson, L. E., Fan, L. T., and Fox, V. G. Heat and mass transfer in the laminar boundarylayer flow of a moving flat surface with constant surface velocity and temperature focusing on theeffects of suction/injection. Industrial & Engineering Chemistry Fundamentals, 5, 19–25 (1966) |
| [4] | Liu, I. C. A note on heat and mass transfer for a hydromagnetic flow over a stretching sheet.International Communications in Heat and Mass Transfer, 32(8), 1075–1084 (2005) |
| [5] | Hammad, M. A. A. and Ferdows, M. Similarity solutions to viscous flow and heat transfer ofnanofluid over nonlinearly stretching sheet. Applied Mathematics and Mechanics (English Edi-tion), 33(7), 923–930 (2012) DOI 10.1007/s10483-012-1595-7 |
| [6] | Ali, F. M., Nazar, R., Arifin, N. M., and Pop, I. MHD stagnation-point flow and heat transfer to-wards stretching sheet with induced magnetic field. Applied Mathematics and Mechanics (EnglishEdition), 32(4), 409–418 (2011) DOI 10.1007/s10483-011-1426-6 |
| [7] | Kumaran, V. and Ramanaiah, G. A note on the flow over a stretching sheet. Acta Mechanica116(1-4), 229–233 (1996) |
| [8] | Ali, M. E. On thermal boundary layer on a power law stretched surface with suction or injection.International Journal of Heat and Mass Transfer, 16, 280–290 (1995) |
| [9] | Elbashbeshy, E. M. A. Heat transfers over an exponentially stretching continuous surface withsuction. Archives of Mechanics, 53(6), 643–651 (2001) |
| [10] | Sanjayanand, E. and Khan, S. K. On heat and mass transfer in a viscoelastic boundary layer flowover an exponentially stretching sheet. International Journal of Thermal Sciences, 45, 819–828(2006) |
| [11] | Magyari, E. and Keller, B. Heat and mass transfer in the boundary layers on an exponentiallystretching continuous surface. Journal of Physics D: Applied Physics, 32, 577–585 (1999) |
| [12] | Nadeem, S., Zaheer, S., and Fang, T. Effects of thermal radiations on the boundary layer flow ofa Jeffrey fluid over an exponentially stretching surface. Numerical Algorithms, 57, 187–205 (2011) |
| [13] | Nadeem, S. and Lee, C. Boundary layer flow of nanofluid over an exponentially stretching surface.Nanoscale Research Letters, 7, 94 (2012) |
| [14] | Liao, S. J. Beyond Perturbation: Introduction to the Homotopy Analysis Method, Chapman andHall/CRC, Boca Raton, 99–102 (2003) |
| [15] | Liao, S. J. On a generalized Taylor theorem: a rational proof of the validity of the homotopyanalysis method. Applied Mathematics and Mechanics (English Edition), 24(1), 53–60 (2003)DOI 10.1007/BF02439377 |
| [16] | Zhu, J., Zheng, L. C., and Zhang, X. X. Analytical solution to stagnation-point flow and heattransfer over a stretching sheet based on homotopy analysis. Applied Mathematics and Mechanics(English Edition), 30(4), 463–474 (2009) DOI 10.1007/s10483-009-0407-2 |
| [17] | Nadeem, S. and Hussain, A. MHD flow of a viscous fluid on a nonlinear porous shrinking sheetwith homotopy analysis method. Applied Mathematics and Mechanics (English Edition), 30(12),1569–1578 (2009) DOI 10.1007/s10483-009-1208-6 |
| [18] | Liao, S. J. Homotopy Analysis Method in Nonlinear Differential Equations, Springer & HigherEducation Press, Heidelberg (2012) |
| [19] | Liao, S. J. An optimal homotopy-analysis approach for strongly nonlinear differential equations.Communications in Nonlinear Science and Numerical Simulation, 15, 2003–2016 (2010) |
| [20] | Wang, Q. The optimal homotopy-analysis method for Kawahara equation. Nonlinear Analysis:Real World Applications, 12, 1555–1561 (2011) |
| [21] | Nadjafi, J. S. and Jafari, H. S. Comparison of Liao’s optimal HAM and Niu’s one-step optimalHAM for solving integro-differential equations. Journal of Applied Mathematics & Bioinformatics,1(2), 85–98 (2011) |
| [22] | Niu, Z. and Wang, C. A one-step optimal homotopy analysis method for nonlinear differential.Communications in Nonlinear Science and Numerical Simulation, 15, 2026–2036 (2010) |
| [23] | Fan, T. and You, X. Optimal homotopy analysis method for nonlinear differential equations inthe boundary layer. Numerical Algorithms, 62, 337–354 (2013) |
| [24] | Williamson, R. V. The flow of pseudoplastic materials. Industrial & Engineering Chemistry,21(11), 1108–1111 (1929) |
| [25] | Lyubimov, D. V. and Perminov, A. V. Motion of a thin oblique layer of a pseudoplastic fluid.Journal of Engineering Physics and Thermophysics, 75(4), 920–924 (2002) |
| [26] | Nadeem, S. and Akram, S. Influence of inclined magnetic field on peristaltic flow of a Williamsonfluid model in an inclined symmetric or asymmetric channel. Mathematical and Computer Mod-elling, 52, 107–119 (2010) |
| [27] | Nadeem, S. and Akbar, N. S. Numerical solutions of peristaltic flow of Williamson fluid withradially varying MHD in an endoscope. International Journal for Numerical Methods in Fluids,66(2), 212–220 (2010) |
| [28] | Nadeem, S. and Akram, S. Peristaltic flow of a Williamson fluid in an asymmetric channel. Com-munications in Nonlinear Science and Numerical Simulation, 15, 1705–1716 (2010) |
| [29] | Dapra, I. and Scarpi, G. Perturbation solution for pulsatile flow of a non-Newtonian Williamsonfluid in a rock fracture. International Journal of Rock Mechanics and Mining Sciences, 44, 271–278(2007) |
| [30] | Nadeem, S., Hussain, S. T., and Lee, C. Flow of a Williamson fluid over a stretching sheet.Brazilian Journal of Chemical Engineering, 30(3), 619–625 (2013) |
 2013, Vol. 35
2013, Vol. 35







































