Shanghai University
Article Information
- S. ASGHAR, Q. HUSSAIN, T. HAYAT, F. ALSAADI. 2014.
- Modified iterative method for augmented system∗
- Appl. Math. Mech. -Engl. Ed., 35(4): 515-534
- http://dx.doi.org/10.1007/s10483-014-1881-6
Article History
- Received 2013-4-15;
- in final form 2013-5-15
The iterative method to the large sparse 2×2 block linear system of equations
is considered,where the matrix A is m × m symmetric positive definite (SPD),the matrix B is m × n and has a full column rank,i.e.,rank (B) = n,vectors x,p ∈ Rm ,vectors y,q ∈ Rn ,and superscript T stands for the transpose. Under these assumptions,the above linear system has a unique solution. The linear system (1) is important for many different applications of science computing [1, 2, 3, 4] ,such as fluid dynamics,the finite element method for solving the Navier-Stokes equation,constrained optimization,constrained or generalized least squares problems,image processing,and linear elasticity.Since the above problem is large and sparse,the iterative methods for solving (1) are effective because of storage requirements and preservation of sparsity. The well-known successive overrelaxation-like (SOR) [5] and accelerated over-relaxation (AOR) [6] methods are simple iterative methods,which are popular in engineering applications. The difficulty for the SOR and AOR methods is the singularity of the block diagonal part of the coefficient matrix of the system (1). Recently,there have been several proposals [7, 8, 9, 10, 11, 12] for generalizing the SOR method for the above system. However,the most practical and important generalization of the SOR method is the SOR-like method given by Golub et al. [7] . The SOR-like method is more closely related to the format of the normal SOR splitting as follows:



In Section 2,we discuss the convergence analysis of the MSOR-like method,and in Section 3,we derive the convergence domain. In Section 4,the optimum for the MSOR-like are given. In Section 5,a numerical example is given to show the effectiveness of the MSOR-like method. 2 Basic functional equation and lemmas
If we let Mω be the iteration matrix of the MSOR-like method and note that


If we let λ be an eigenvalue of Mω and (u,v) T be the corresponding eigenvector,we have
which is equivalent toLemma 2.1If λ is an eigenvalue of Mω ,then λ ≠ 1.
Proof If λ = 1,and the associated eigenvector is (u,v)T ,then following from (9) and ω ≠ 0,we have
resulting in Q −1 B T A −1 Bv = 0. Since Q−1BTA−1B is nonsingular,we have that v = 0. It follows from (10) that u = 0. This contradicts to (u,v)T ,which is an eigenvector of the iteration of Mω . Hence,λ ≠ 1,concluding the proof.Lemma 2.2 If m > n,then λ = 1 − ω ≠ 0 is an eigenvalue of Mω at least with multiplicity of m − n. If m = n,then λ = 1 − ω ≠ 0 is not an eigenvalue of Mω .
Proof If λ = 1 − ω ≠ 0 is an eigenvalue of Mω ,then there exists a nonzero vector (u,v)T so that they satisfy the system (8) with λ = 1 − ω ≠ 0. Therefore,by the system (9) and ω ≠ 0, we have


Theorem 2.1 Let Mω be the iteration matrix of the MSOR-like method. Then,
(i) λ = 1 − ω ≠ 0 is an eigenvalue of Mω ,if m > n.
(ii) For any eigenvalue λ (λ ≠ 1 − ω) of Mω ,there is an eigenvalue µ of Q−1BTA−1B so that λ and ω satisfy the following functional equation:
(iii) For any eigenvalue µ of Q−1BTA−1B,if λ is different from 1 − ω and 1,and µ and ω satisfy the above functional equation,then λ is an eigenvalue of Mω .
Proof The conclusion (i) of Theorem 2.1 comes from Lemma 2.2.
For the conclusion (ii),we let λ ≠ 1 − ω be the eigenvalue of Mω ,and (u,v)T be the associated eigenvector. Then,they satisfy the system (9). Thus,we have
Since λ ≠ 1 − ω,λ ≠ 1 by Lemma 2.1,and v ≠ 0 by the note after Lemma 2.2,there is an eigenvalue µ of Q−1BTA−1B satisfying the equation µv = Q−1BTA−1Bv. Therefore,(12) is equivalent to (11),concluding the proof of the conclusion (ii).For the conclusion (iii),we let u,v be the eigenvalue and associated eigenvector of the matrix Q−1BTA−1B. Therefore,we have Q−1BTA−1Bv = µv. By the conditions of the theorem,(12) holds. If we let

Thus,λ is an eigenvalue of Mω ,since (u,v)T is nonzero.
Corollary 2.1 If we let ρ(Mω ) be the spectral radius of the MSOR-like iteration matrix Mω and m > n,then we have ρ(Mω ) > |1 − ω|.
Note that by the above corollary,the necessary condition for the convergence of the MSORlike method when m > n is
Lemma 2.3 [5] Both roots of the real quadratic equation λ2 − bλ + c = 0 are less than one in modulus if and only if |c| < 1 and |b| < 1 + c. 3 Convergence analysis
From now on,we always assume that λ and µ are eigenvalues of the iteration matrix Mω of the MSOR-like method and the matrix Q−1BTA−1B,respectively. We also assume that the parameter ω satisfies the inequality (13). Thus,no matter 1 − ω is an eigenvalue of Mω or not,it does not affect the convergence property of the MSOR-like method. Therefore,the MSOR-like method converges if and only if for any eigenvalue µ,the solution λ of (11) is less than unity in modulus. Then,(11) is equivalent to
whereThen,we have the following results.
Theorem 3.1 Assume that the real parameters ω satisfy (6) and (13). If we choose a nonsingular matrix Q so that all eigenvalues of the matrix Q−1BTA−1B are real and positive, then the MSOR-like method converges if and only if
where µmax is the largest eigenvalue of the matrix Q−1BTA−1B.Proof Let S be the set of all eigenvalues µ of the matrix Q−1BTA−1B. Under the assumptions of the theorem,the coefficients of (14) are real. Thus,it follows from Theorem 2.1 and Lemma 2.3 that the MSOR-like method converges if and only if then the MSOR-like method converges if and only if
for any µ ∈ S,which is equivalent to for any µ ∈ S. Since ω satisfies (13),the first inequality of (18) is always true. Besides,µ > 0 for any µ ∈ S. Therefore,0 <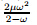 for any µ ∈ S. Hence,(18) is equivalent to (16) since
for any µ ∈ S. Hence,(18) is equivalent to (16) since
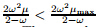 for any µ ∈ S.
for any µ ∈ S.
Thus,we have proved that the MSOR-like method converges if and only if the condition (16) holds.
Theorem 3.2 If we choose a nonsingular matrix Q so that all eigenvalues of the matrix Q−1BTA−1B are real and positive,then the MSOR-like method converges if and only if
Proof Note that the condition (16) is also equivalent to

If we let
then the condition (16) holds if and only if
If we let


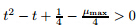 is equivalent to t < t1 or t > t2. Besides,it can be shown that
is equivalent to t < t1 or t > t2. Besides,it can be shown that

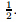 . Hence,the condition (16) holds if and only if
Thus,we have proved that the MSOR-like method converges if and only if the condition (19)
holds.
4 Determination of optimum parameters
. Hence,the condition (16) holds if and only if
Thus,we have proved that the MSOR-like method converges if and only if the condition (19)
holds.
4 Determination of optimum parametersFollowing from (14) and (15),(11) is equivalent to
Therefore,we have

Theorem 4.1 Let A and Q be SPD,and B be of full rank. Assume that all eigenvalues µ of Q−1BTA−1B are real and positive,and ρ(Mω ) is the spectral radius of the MSOR-like iteration matrix Mω . Then,we get
Case 1 then
then

Case 2 then
then

Case 3 then
then

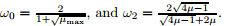
Proof (I) If 1 − 2µ ≠ 0 or µ ≠
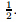 ,and
,and


(i) If µmin >
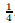 ,then ∆1 > 0.
,then ∆1 > 0.
If we let

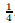 ,ω1 < 0.
,ω1 < 0.
On the other hand,by Theorem 3.2,we have

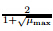 Comparing ω0
and ω2,we get
Comparing ω0
and ω2,we get

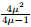 and ω2 < ω0
. Letting s(µ) =
and ω2 < ω0
. Letting s(µ) =
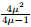 ,since
,since 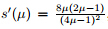 ,we get the
following conclusions:
,we get the
following conclusions:
If µ <
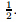 ,s(µ) is a monotone decreasing function. If µ >
,s(µ) is a monotone decreasing function. If µ >
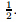 ,s(µ) is a monotone increasing
function.
,s(µ) is a monotone increasing
function.
Therefore,if
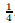 < µmin ≤
< µmin ≤
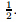 and µmax < 1 or µmin >
and µmax < 1 or µmin >
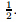 and µmax <
and µmax <
 ,ω2 ≤ ω0
. By
Theorem 3.2,when ω2 < ω ≤ ω0,∆ > 0; when 0 < ω ≤ ω2,∆ ≤ 0.
,ω2 ≤ ω0
. By
Theorem 3.2,when ω2 < ω ≤ ω0,∆ > 0; when 0 < ω ≤ ω2,∆ ≤ 0.
If
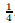 < µmin <
< µmin <
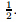 and µmax > 1 or µmin >
and µmax > 1 or µmin >
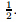 and µmax ≥
and µmax ≥
 ,ω2 > ω0. By Theorem 3.2,
when 0 < ω ≤ ω0,∆ < 0.
,ω2 > ω0. By Theorem 3.2,
when 0 < ω ≤ ω0,∆ < 0.
(ii) If µmin <
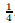 ,then ∆1 < 0.
,then ∆1 < 0.
When 0 < ω ≤ ω0,h(ω) > 0 is always true,i.e.,∆ > 0 is always true.
(iii) If µ =
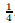 ,then ∆1 = 0.
When 0 < ω ≤ω0,h(ω) = (1 −
,then ∆1 = 0.
When 0 < ω ≤ω0,h(ω) = (1 −
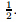 )
2
ω
2
=
)
2
ω
2
=
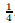 ω
2
> 0 is always true,i.e.,∆ > 0 is always true.
ω
2
> 0 is always true,i.e.,∆ > 0 is always true.
(II) If 1 − 2µ = 0 or µ =
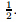 ,then h(ω) = 4ω − 4,it is easy to obtain that ∆ ≥0 if ω ≥ 1;
∆ ≤ 0 if ω < 1.
,then h(ω) = 4ω − 4,it is easy to obtain that ∆ ≥0 if ω ≥ 1;
∆ ≤ 0 if ω < 1.
We immediately obtain

Theorem 4.2 Let A and Q be SPD,and B be of full rank. Assume that all eigenvalues µ
of Q−1BTA−1B are real and positive,ρ(Mω
) is the spectral radius of the MSOR-like iteration
matrix Mω
,ρ(Mωb
) is the minimum of ρ(Mω
),and ωb
is the optimum relaxation factor. Then,
µmin >
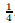 ,we have the following two cases.
Case 1 If µmax ≤
,we have the following two cases.
Case 1 If µmax ≤
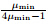 ,we get
,we get

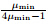 ,we ge
,we ge

Proof From Theorem 4.1,(23) is equivalent to




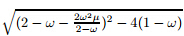 = 0. Thus,∆ = 0. Since
µmin >
= 0. Thus,∆ = 0. Since
µmin >
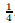 ,it is easy to get ωb = ω2 =
,it is easy to get ωb = ω2 =
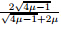 Letting
Letting
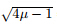 = t and ωb =
= t and ωb =
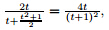 we can get
we can get 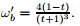 . Therefore,
. Therefore,

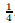 < µ <
< µ <
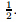 ,then ρ
2
(Mω
) is a monotonically decreasing function. If t > 1 or µ >
,then ρ
2
(Mω
) is a monotonically decreasing function. If t > 1 or µ >
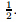 ,
then ρ
2
(Mω
) is a monotonically increasing function (see Fig. 1)
,
then ρ
2
(Mω
) is a monotonically increasing function (see Fig. 1)
 |
| Fig. 1 Monotone of ρ 2 (Mω) |
(i) If ρ µmin (Mω ) > ρ µmax (Mω )(see Fig. 2),it is equivalent that

 |
| Fig. 2 Monotone of ρ 2 (Mω)if ρµ min (Mω) ≥ ρµmax (Mω) |


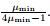 .
.
Therefore,if µmax ≤
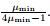 ,then ρ
2
(Mωb
) =
,then ρ
2
(Mωb
) =
 . If µmin >
. If µmin >
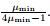 ,then
ρ
2
(Mωb
) =
,then
ρ
2
(Mωb
) =
 .
.
(ii) If ρ µmin (Mω ) < ρµmax (Mω )(see Fig. 3),the proof of Case 2 of Theorem 4.2 is similar to that of Case 1 of Theorem 4.2. Therefore,we omit the proof of Case 2.
 |
| Fig. 3 Monotone of ρ 2 (Mω)if ρµ min (Mω) < ρµmax (Mω) |
Theorem 4.3 Let A and Q be SPD,and B be of full rank. Assume that all eigenvalues of Q−1BTA−1B are real and positive,and µ are eigenvalues of the iteration matrix of the matrix Q−1BTA−1B. Let ρ(Mω ),ρ(Ω),and ρ(M ) be the spectral radii of the MSOR-like method, MSSOR-like [10] method,and SOR-like [8] method iteration matrix,respectively. Then,we get the following result,which is a criterion for choosing between the MSOR-like,MSSOR-like,and the SOR-like methods to solve augmented systems.



Thus,the theorem is proved. 5 Numerical example
In this section,we give the example to illustrate the MSOR-like method to find the solution of the related augmented systems and compare the results of the MSOR-like method,the MSSOR-like method [10] ,and the SOR-like method [8] .
Example 1 [8] Consider the augmented linear system (1),in which


 being the Kronecker product symbol and h =
being the Kronecker product symbol and h =
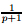 the discretization mesh-size.
the discretization mesh-size.
We set m = 2p2
and n = p2
. We choose the preconditioning matrix Q = B
T
 −1
B,
−1
B,
 =tridiag(A) for the MSOR-like,the MSSOR-like,and SOR-like methods. The stopping criterion
=tridiag(A) for the MSOR-like,the MSSOR-like,and SOR-like methods. The stopping criterion
 < 10
−6
is used in the computations,where
< 10
−6
is used in the computations,where

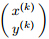 is the kth iteration for each of the methods. All the computations are done on
INTEL PENTIUM1.8 GHZ (256 M RAM),Windows XP system by using MATLAB 7.0. The
parameters,number of iterations (IT) and CPU in seconds for convergence needed for the
MSOR-like,the MSSOR-like,and the SOR-like methods are listed in Table 1 .
is the kth iteration for each of the methods. All the computations are done on
INTEL PENTIUM1.8 GHZ (256 M RAM),Windows XP system by using MATLAB 7.0. The
parameters,number of iterations (IT) and CPU in seconds for convergence needed for the
MSOR-like,the MSSOR-like,and the SOR-like methods are listed in Table 1 .
By observing the example,if the conditions of Theorem 4.3 are satisfied,it is not difficult to find that the MSOR-like method is superior to the MSSOR-like method and the SOR-like method. 6 Conclusions
In this paper,the MSOR-like method has been established to solve the saddle point problems, which is a simple and powerful scheme to solve (1). The convergence analysis has been given. We derive its optimal iteration parameter ωb. From Theorem 4.3 and numerical example,it is not difficult to find that the MSOR-like method is superior to the MSSOR-like method and the SOR-like method if the conditions of Theorem 4.3 are satisfied.
| [1] | Wright, S. Stability of augmented system factorizations in interior-point methods. SIAM J. Matrix Anal. Appl., 18(1), 191–222 (1997) |
| [2] | Elman, H. and Golub, G. H. Inexact and preconditioned Uzawa algorithms for saddle point problems. SIAM J. Numer. Anal., 31(11), 1645–1661 (1994) |
| [3] | Fischer, B., Ramage, A., Silvester, D. J., and Wathen, A. J. Minimum residual methods for augmented systems. BIT, 38(5), 527–543 (1998) |
| [4] | Young, D. M. Iterative Solutions of Large Linear Systems, Academic Press, New York, 15–32(1971) |
| [5] | Hadjidimos, A. Accelerated overrelaxation method. Math. Comp., 32(1), 149–157 (1978) |
| [6] | Li, C. J. and Evans, D. J. A new iterative method for large sparse saddle point problem. International Journal of Computer Mathematics, 74(5), 529–536 (2000) |
| [7] | Golub, G. H., Wu, X., and Yuan, J. Y. SOR-like methods for augmented systems. BIT, 41(1),71–85 (2001) |
| [8] | Li, C. J., Li, B. J., and Evans, D. J. Optimum accelerated parameter for the GSOR method. Neural, Parallel & Scientific Computations, 7(4), 453–462 (1999) |
| [9] | Li, C. J., Li, B. J., and Evans, D. J. A generalized successive overrelaxation method for least squares problems. BIT, 38(3), 347–355 (1998) |
| [10] | Wu, S. L., Huang, T. Z., and Zhao, X. L. A modified SSOR iterative method for augmented systems. Journal of Computational and Applied Mathematics, 228(4), 424–433 (2009) |
| [11] | Shao, X. H., Li, Z., and Li, C. J. Modified SOR-like method for the augmented system. International Journal of Computer Mathematics, 184(11), 1653–1662 (2007) |
| [12] | Varga, R. S. Matrix Iterative Analysis, Englewood Cliffs, Prentice-Hall, New Jersey, 110–111(1962) |
 2013, Vol. 35
2013, Vol. 35



























