Shanghai University
Article Information
- S. ASGHAR, Q. HUSSAIN, T. HAYAT, F. ALSAADI. 2014.
- Long time behavior of solutions to coupled Burgers-complex Ginzbury-Landau (Burgers-CGL) equations for flames governed by sequential reaction∗
- Appl. Math. Mech. -Engl. Ed., 35(4): 515-534
- http://dx.doi.org/10.1007/s10483-014-1881-6
Article History
- Received 2012-10-12;
- in final form 2013-5-8
2. Institute of Applied Physics and Computational Mathematics, Beijing 100088, P. R. China
As we know,the uniformly propagating planar premixed flame fronts can become unstable leading to kinds of flame structures,such as pulsating flames,spinning and spiral flames,and flames with traveling or standing waves on the flame fronts [1] . Premixed gaseous flames generally involve many reactants and many reactions,and the simplest model is the case of a single limiting reactant and called one-stage chemical reaction. In premixed gaseous flames with a one-stage chemical reaction,there are two kinds of diffusional thermal instability,the first one is called the monotonic instability,whose spatio-temporal evolution is governed by the KuramotoSivashinsky (KS) equation [2] ,the other one is relative to the oscillatory instability which occurs with a non-zero wave number and frequency at the instability threshold,and its nonlinear evolution is described by complex Ginzburg-Landau(CGL) equations [3] .
However,the actual chemical kinetics governing the structure of flames can be quite complex, and the effect of complex chemical kinetics on the dynamics of propagating flame fronts is governed by the two-stage sequential reaction,which leads to the occurrence of two flame fronts with various regimes of propagation [4, 5] . One of the possible regimes of propagation is that of two planar uniformly propagating fronts with a constant separation distance between them. A linear stability analysis of this regime for the sequential reaction problem showed that,as in the case of a one-stage reaction,the flame fronts can become unstable with respect to either monotonic or oscillatory instabilities [6] . The nonlinear interaction between the monotonic and oscillatory modes of instability of the two uniformly propagating flame fronts can be governed by the following coupled KS-CGL equations [7] :
The system of coupled equations (1) and (2) describes the interaction of the evolving monotonic and oscillatory modes of instability of the uniform flame fronts. Specifically,when m > 0 and ξ = 1,both monotonic and oscillatory modes are excited. In the case of m > 0 and ξ = −1,the oscillatory mode is excited and the monotonic mode is damped. However,when the monotonic mode is excited and the oscillatory mode is damped,m< 0,and g = 0,and the interaction between the excited oscillatory mode and the damped monotonic mode will be described by a complex Ginzburg-Landau equation for P coupled to a Burgers equation for Q, the system equations of coupled KS-CGL equations (1) and (2) are simplified to the following Burgers-CGL equations [7] :
where P (x,t) is the rescaled complex amplitude of the flame oscillations,and Q(x,t) is the deformation of the first front. u and v are the Landau coefficients,and r1 and w are the coupling coefficients. The parameters r1 is complex,r1 = r1r + ir1i ,and all other parameters are real.If there are no coupling with the monotonic mode (terms with Q in (3)),(3) would be the well-known complex Ginzburg-Landau equation that usually describes the weakly nonlinear evolution of a long-scale instability [8] . And if the coupling coefficient w is zero in (4),then (4) would be the well-known Burgers equation [9] . There are so many works concerning the CGL equation [10, 11, 12, 13, 14] and Burgers equation [15, 16, 17] physically and mathematically.
However,there is few work to consider the existence,the uniqueness,and the long time behavior of the solutions for the coupled Burgers-CGL equations (3)−(4) mathematically. In this paper,we consider the following periodic initial value problem for the Burgers-CGL equations in one-dimensional version:
where Ω = [−L,L],and 2L is the period. ξ > 0,w > 0,f (x),and g(x) are given real functions.In what following,we will study the existence and uniqueness of the global smooth solutions to the periodic initial value problem (5)−(8),and then we will prove the existence of the global attractor and establish the estimates of the upper bounds of Hausdorff and fractal dimensions for the attractor. The rest of paper is organized as follows. In Section 2,we briefly give some notations and preliminaries. In Section 3,we establish a prior estimates for the solutions to the periodic initial value problem (5)−(8) and obtain the existence for the solutions. In Section 4,the global attractor A ⊂ H 2 (Ω) × H 3 (Ω) for the periodic initial value problem are obtained. In Section 5,we establish the estimates of the upper bounds of Hausdorff and fractal dimensions for the attractor. In the last Section 6,we make some conclusions. 2 Notations and Preliminaries
Throughout this paper,we denote the spaces of complex valued functions and real valued functions by the same symbols,and denote by ||·|| the norm of L 2 (Ω) with the usual inner product (·,·),||·|| L p denotes the norm of L p (Ω) for 1 ≤ p ≤ ∞ (||·|| = ||·|| 2). W k,p (Ω) is the usual kth order Sobolev space with its norm ||u|| W k,p (Ω) . When p = 2,we write ||·|| H k =||·|| W k,2 (Ω) . Generally,||·||X denotes the norm of any Banach space X. L ∞ (0,T ; T) denotes the space of functions u(x,t) which belong to X as functions of x for every t (0 ≤ t ≤ T ). Without any ambiguity,we denote a generic positive constant by C which may vary from line to line,and Ci ,E i ,k i ,and κ i (i = 1,2,· · · ) are the positive constants depending on the known values.
In the following sections,we will use the following inequalities.
Lemma 2.1 (Gagliardo-Nirenberg inequality) [18] Let Ω be a bounded domain with ∂Ω in C m ,and let u be any function in W m,r (Ω) ∩L q (Ω),1 ≤ q,r ≤ ∞. For any integer j ,0 ≤ j < m, and for any number a in the interval j/m ≤ a ≤ 1,set

Lemma 2.2 (Generalization of the Sobolev-Lieb-Thirring inequality) [19] Assume that Ω ⊂ R n is of class C 2m or it enjoys the prolong property,and we denote by |Ω| the volume of Ω. Let φj ,1 ≤ j ≤ N,be a finite family of H m (Ω) which is orthonormal in L 2 (Ω) and set,for almost every x ∈ Ω,



Especially,when  and m = 1,
and m = 1,
In this section,we obtain the existence and uniqueness of the solutions for the periodic initial value problem (5)−(8). Firstly,we establish some a prior estimates for the solutions.
Lemma 3.1 Assume that P0(x) ∈ L 2 (Ω),Q0(x) ∈ H 1 (Ω),f (x) ∈ L 2 (Ω),g (x) ∈ L 2 (Ω), and suppose that 2r1r − 1 > 0. Then for the solutions of the problem (5)−(8),we have
where the constants E0 and E1 depend on ||P (0)|| and ||Qx (0)||.Proof Firstly,we differentiate (6) with respect to x once and set
then (5) and (6) are changed into Then,multiplying (14) by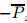 ,integrating with respect to x over Ω and taking the real part,we
can get
where
From (16) and (17),we have
,integrating with respect to x over Ω and taking the real part,we
can get
where
From (16) and (17),we have
On the other hand,multiplying (15) by W and integrating over Ω,we have
where Then from (19),(20),and (21),there holdsMultiplying (18) by 2ω and (22) by (2r1r − 1) respectively,and adding theses two equations together,we can get
Noting the condition 2rr1 − 1 > 0,we have and Combining (23)−(25) together yieldsFrom Hölder’s inequality,2w||P|| 2 ≤ 2w∫Ω |P| 4 dx + C(|Ω|). Since∫Ω W dx = ∫ -L L Qx dx = Q| -L L = 0,applying Poincar´e’s inequality,we can get ||W|| 2 ≤CW||Wx|| 2 ,where CW is a positive constant. Therefore,we have
which implies where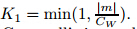
By Gronwall’s inequality,we infer that
Therefore, Combining the transformation (13),the proof of Lemma 3.1 is completed.Lemma 3.2 Under the conditions of Lemma 3.1,and assume that P0(x) ∈ H 1 (Ω),Q0(x) ∈ H 2 (Ω),f (x) ∈ L 2 (Ω),g(x) ∈ H 1 (Ω). Then for the solutions of the problem (5)−(8),we have
where the constant E2 depends on ||Px (0)|| and ||Qxx (0)||.Proof Similarly to the first step in the proving the Lemma 3.1,we can make use of the
transformed equations. Firstly,multiplying (14) by (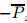 xx
),integrating with respect to x over
Ω and taking the real part,we can get
xx
),integrating with respect to x over
Ω and taking the real part,we can get
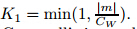 in (37),we can obtain
Similarly,from the Gagliardo-Nirenberg inequality,Lemma 3.1,and (37),there holds
and
On the other hand,from (36),we can also have
and
For the next term,we can compute that in the same way,
For the last two terms,we use Hölder’s inequality to obtain
Substituting (39)−(45) into (35),we have
From (37) and (38) again,we find
Thus,combining the transformation (13),we have
By Gronwall’s inequality,we get
where the constant E2
depends on ||Px
(0)|| and ||Qxx
(0)||.
in (37),we can obtain
Similarly,from the Gagliardo-Nirenberg inequality,Lemma 3.1,and (37),there holds
and
On the other hand,from (36),we can also have
and
For the next term,we can compute that in the same way,
For the last two terms,we use Hölder’s inequality to obtain
Substituting (39)−(45) into (35),we have
From (37) and (38) again,we find
Thus,combining the transformation (13),we have
By Gronwall’s inequality,we get
where the constant E2
depends on ||Px
(0)|| and ||Qxx
(0)||.Furthermore,combining (48) and (49),we can also obtain that
where C is a positive constant. The proof of Lemma 3.2 is completed.Corollary 3.1 Under the conditions of Lemma 3.1 and Lemma 3.2,the solutions of the problem (5)−(8) satisfy
where C are positive constants.Proof According to Agmon’s inequality,we can conclude the corollary easily.
Lemma 3.3 Under the conditions of Lemma 3.1 and Lemma 3.2,then for the solutions of the problem (5)−(8),we have
where C are positive constants. Proof Considering (6),we multiply this equation by Q and integrate over Ω,then we have By the previous lemmas and the corollary (51),we can get and Substituting (53) and (54) into (52),we find that By Gronwall’s inequality and Agmon’s inequality,we can complete the proof of Lemma 3.3.Lemma 3.4 Under the conditions of Lemma 3.2,assume that P0(x) ∈ H 2 (Ω),Q0(x) ∈ H 3 (Ω),f (x) ∈ H 1 (Ω),and g(x) ∈ H 2 (Ω). Then,we have the following estimates:
where the constant E3 depends on ||Pxx (0)|| and ||Qxxx (0)||.Proof In the same way,taking inner product of (14) with xxxxx and taking the real part, and multiplying (15) by Wxxxx and integrating with respect to x,then adding together yields
According to the Gagliardo-Nirenberg inequality,Lemma 3.1,and Lemma 3.2,we have Similarly,we have where ε 3 and ε 4 are positive constants. Thus,by choosing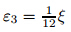 in (58),we can obtain
According the above lemmas and Corollary 3.1,there is
From Lemma 3.2 and Corollary 3.1,we know that ||Wx
|| = ||Qxx
|| ≤ C and ||W ||
L∞
=
||Qx||
L∞≤ C,then according to the Gagliardo-Nirenberg inequality,we have
From (59),we have
Similarly to getting (63),we can also obtain that
For the next term,we have
At last,we can compute the last two terms by Hölder’s inequality as
Then combining (57)−(66),there holds
From (58) and (59) again,we find
Thus,by virtue of the transformation (13),there holds
According to Gronwall’s inequality,we can obtain
where the constant E3
depends on ||Pxx
(0)|| and ||Qxxx
(0)||.
in (58),we can obtain
According the above lemmas and Corollary 3.1,there is
From Lemma 3.2 and Corollary 3.1,we know that ||Wx
|| = ||Qxx
|| ≤ C and ||W ||
L∞
=
||Qx||
L∞≤ C,then according to the Gagliardo-Nirenberg inequality,we have
From (59),we have
Similarly to getting (63),we can also obtain that
For the next term,we have
At last,we can compute the last two terms by Hölder’s inequality as
Then combining (57)−(66),there holds
From (58) and (59) again,we find
Thus,by virtue of the transformation (13),there holds
According to Gronwall’s inequality,we can obtain
where the constant E3
depends on ||Pxx
(0)|| and ||Qxxx
(0)||.Furthermore,combining (69) and (70),we can also obtain that
where C is a positive constant. Thus,the proof of Lemma 3.4 is completed.Corollary 3.2Under the conditions of Lemma 3.1 and Lemma 3.4,the solutions of the problem (5)−(8) satisfy

From the results of Lemma 3.1−Lemma 3.4,we find that
where C depends only on ||P0|| H 2 ,||Q0|| H 3 ,and T . Thus,by the standard methods,we can extend the local solutions P (x,t),Q(x,t) of the problem (5)−(8) to global solutions,that is,we have the following theorem.Theorem 3.1Suppose that P0(x) ∈ H 2 (Ω),Q0(x) ∈ H 3 (Ω),f (x) ∈ H 1 (Ω),g(x) ∈ H 2 (Ω) and suppose that 2r1r − 1 > 0. Then the problem (5)−(8) has unique solutions P (x,t),Q(x,t) satisfying

In this section,we construct the global attractor for the problem (5)−(8). We first note that by Theorem 3.1,there exists a dynamical system S(t)(t≥0) which maps H 2 (Ω) × H 3 (Ω) to H 2 (Ω) × H 3 (Ω)such that S(t)(u 0,Q0) = (P (t),Q(t)),the solutions of problem (5)−(8).
In order to obtain the existence of the global attractor associated with semigroup S(t),we need uniform a priori estimates in time. From (29),when ||P0 || ≤ R and ||Q0 || H 1 ≤ R,we have
where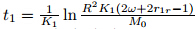 depends on the data (f,g,R) when ||P0
|| ≤ R ,and ||Q0
||
H
1 ≤ R
depends on the data (f,g,R) when ||P0
|| ≤ R ,and ||Q0
||
H
1 ≤ R
Applying (73),(74) and repeating the procedure of Lemma 3.2,we can derive that
where C1 is a constant depending on the data (f,g) and the known parameters.By Gronwall’s inequality and (75),we find that when t ≥t1,there is
where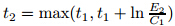 depends on the data (f,g,R) when ||P0
||
H
1 ≤ R,||Q0
||
H
2≤R.
depends on the data (f,g,R) when ||P0
||
H
1 ≤ R,||Q0
||
H
2≤R.
Applying (73),(76),and repeating the procedure of the proof of Lemma 3.4,we obtain that
where C2depends on the data (f,g) and the known parameters.Similarly to (76),by Gronwall’s inequality and Lemma 3.4,we can derive that
where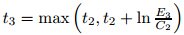 depends on the data (f,g,R) when ||P0
||
H
2≤ R,||Q0
||
H
3 ≤ R.
We observe that (73),(74),(76),and (78) imply that
where K is a positive constant.
depends on the data (f,g,R) when ||P0
||
H
2≤ R,||Q0
||
H
3 ≤ R.
We observe that (73),(74),(76),and (78) imply that
where K is a positive constant.
In what follows,we are going to show that the semigroup S(t) : H 2 (Ω) × H 3 (Ω) → H 2 (Ω) × H 3 (Ω) is compact for large t.
Lemma 4.1Assume that the conditions of Theorem 3.1 hold,and suppose that f ∈ H 2 (Ω),g ∈ H 3 (Ω). Then,for the solutions of the problem (5)−(8),we have
where the constant E4 depends on ||f xx ||,||g xxx ||,and R when ||P0 || H 2≤R,||Q0 || H 3≤R.Proof Firstly by virtue of the transformed equations (14)−(15),taking the inner product
of (14) with 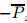 xxxxxx
over Ω,taking the real part,we can obtain
xxxxxx
over Ω,taking the real part,we can obtain
Remembering the transformation (13),this implies that
On the other hand,integrating (77) between tand t + 1,and applying (78),we find that Thus,by the uniform Gronwall lemma,it follows from (91) and (92) that which concludes the proof of Lemma 4.1.In order to prove the existence of global attractor of problem (5)−(8),we need the following result:
Theorem 4.1 [10] We assume that H is a metric space and that the nonlinear operator S(t) of H into itself for t≥0 satisfies

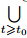 S(t)B0
is relatively compact in H.
We also assume that there exists an open setU and a bounded set B of U such that B is
absorbing in U .
S(t)B0
is relatively compact in H.
We also assume that there exists an open setU and a bounded set B of U such that B is
absorbing in U .
Then the ω-limit set of B:  is a compact attractor,which attracts
the bounded set of U . It is the maximal bounded attractor in U .
is a compact attractor,which attracts
the bounded set of U . It is the maximal bounded attractor in U .
Theorem 4.2Assume that the conditions of Theorem 3.1 hold,and suppose that f ∈ H 2 (Ω),g ∈ H 3 (Ω). Then there exists a global attractor A ⊂ H 2 (Ω) × H 3 (Ω) for the periodic initial problem (5)−(8),i.e.,there is a set A such that
(i) StA = A,t ∈ R + ;
(ii)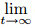 dist(S(t)B,A) = 0,for any bounded set B ⊂ H
2
(Ω) × H
3
(Ω),where
dist(S(t)B,A) = 0,for any bounded set B ⊂ H
2
(Ω) × H
3
(Ω),where

Proof On account of the result of Theorem 4.1,we will prove this theorem by checking the conditions in Theorem 4.1.
We observer that (79) shows that the ball

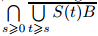 is a compact attractor on
H
2
(Ω) × H
3
(Ω),where the closure is taken in H
2
(Ω) × H
3
(Ω).
is a compact attractor on
H
2
(Ω) × H
3
(Ω),where the closure is taken in H
2
(Ω) × H
3
(Ω).
This completes the proof of Theorem 4.2. 5 Dimension of global attractor
In this section,we prove that the global attractor A as a compact subset of H 2 (Ω) × H 3 (Ω) has a finite Hausdorff dimension and a fractal dimension. To this end,we consider the first variation equation of (5)−(8) as follows:
with the initial value and the periodic boundary conditions where (U0,V0) ∈ H 2 (Ω) × H 3 (Ω),and (P (t),Q(t)) = S(t)(P0,Q0) is the solution of (5)−(8) with (P0,Q0) ∈ A.Given (P0,Q0) ∈ A and the solution S(t)(P0,Q0) ∈H 2 (Ω) × H 3 (Ω),by standard methods we can easily prove that for any (U0,V0) ∈ H 2 (Ω) × H 3 (Ω),the linear initial boundary value problem (94)−(97) possesses a unique solution

Let Y0 = (P0,Q0),Z0 = (U0,V0 ),denote by Y (t) = S(t)Y0,Z (t) = (U (t),V (t)) = DS(t)Z0 the solution of (94)−(97). We now show S(t) is uniformly differentiable on the bounded set of H 2 (Ω) × H 3 (Ω). More precisely,we have
Lemma 5.1 Let R and T be two positive numbers. Then,there exists a constant C depending on R and T such that for every Y0,Z0,t satisfying ||Y0 || H 2 ×H 3 ≤ R,||Y0 + Z0 || H 2 ×H 3 ≤ R,0 ≤ t ≤ T ,we have

The proof of this result,which is lengthy but classical,is omitted here. For the techniques used,we refer readers to [19] and references therein. Note that Lemma 5.1 shows that S(t) is uniformly differentiable on A.
Now,we study the transformation of m-dimensional volumes inH 2 (Ω) × H 3 (Ω)by the operator DS(t)Y0,Y0 ∈ A. Denote by Z1(t),Z2(t),· · · ,ZN (t) the solution of linear equations (94)−(97) corresponding respective to the initial data

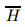 = L
2
(Ω) × H
1
(Ω),j = 1,2,· · · ,N . By the simple computation,we can deduce
that
where L(Y (t)) = L(S(t)Y0
) is a linear map L(t,Y0)ξ = Z (t). ∧ denotes the exterior product,
Tr the trace of the operator,and QN(t) the orthogonal projection of space
= L
2
(Ω) × H
1
(Ω),j = 1,2,· · · ,N . By the simple computation,we can deduce
that
where L(Y (t)) = L(S(t)Y0
) is a linear map L(t,Y0)ξ = Z (t). ∧ denotes the exterior product,
Tr the trace of the operator,and QN(t) the orthogonal projection of space 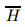 to the spanning
subspace generated by Z1(t),Z2(t),· · · ,ZN(t). Therefore,we can then estimate
to the spanning
subspace generated by Z1(t),Z2(t),· · · ,ZN(t). Therefore,we can then estimate
At a given time τ ,let Φj = (φj ,ψj )
T
be orthonormal basis of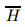 such that
such that


From (101) and (109),we know that
From (10) and (11),the results of the generalization of the Sobolev-Lieb-Thirring inequality, we find that
Substituting (111) into (110),we can get where the last two terms with Young’s inequality have been handled,and κ 4 is a positive constant.Assuming that Y0 belong to the global attractor A,we can majorize the quantity

By application of Proposition V.2.1 and Theorem V.3.3 in Ref. [19],we have thus proved the following theorem.
Theorem 5.1 Assume that the conditions of Theorem 4.2 hold,and and we consider the dynamical system associated with the periodic initial problem (5)−(8). We denote by A the corresponding global attractor whose existence is stated in Theorem 4.2,and let N be defined by (114). Then,the Hausdorff dimension of A is less then or equal to N ,and its fractal dimension is less then or equal to 2N . 6 Conclusions
The coupled Burgers-CGL equations are derived from the nonlinear evolution of the coupled long-scale oscillatory and monotonic instabilities of a uniformly propagating combustion wave governed by a sequential chemical reaction. Thus,it is an interesting topic for mathematicians and other researchers. In this paper,we study the periodic initial value problem (5)−(8) for these coupled equations mathematically. Firstly,the existence and uniqueness of the global smooth solutions are obtained by using some subtle transforms,delicate a priori estimates and so-called continuity method,which assure the well-posedness of the rescaled complex amplitude of the flame oscillations P (x,t)) and the deformation of the first front Q(x,t) in the time [0,T]. Secondly,we consider the long time behavior for these solutions,which study the motions of P (x,t)) and Q(x,t) as t → ∞. We obtain the existence of the global attractor A ⊂ H 2 (Ω) × H 3 (Ω) for problem (5)−(8) and establish the estimates of the upper bounds of Hausdorff and fractal dimensions for the attractor. More precisely,the Hausdorff dimension of A is less then or equal to N ,and its fractal dimension is less then or equal to 2N ,where N is defined in (114). For the physical significance,we know that the rescaled complex amplitude of the flame oscillations P (x,t)) and the deformation of the first front Q(x,t) attract the bounded sets of H 2 (Ω) × H 3 (Ω) as t → ∞ under the initial conditions P0(x)and Q0(x),and the dimensions of the bounded sets are bounded.
| [1] | Williams, F. A. Combustion Theory, Benjamin Cummings, Menlo Park (1985) |
| [2] | Sivashinsky, G. I. Nonlinear analysis of hydrodynamic instability in laminar flames I, derivationof basic equations. Acta Astronautica, 4(11-12), 1177–1206 (1977) |
| [3] | Olagunju, D. O. and Matkowsky, B. J. Coupled complex Ginzburg-Landau type equations in gaseous combustion. Stability and Applied Analysis of Continuous Media, 2, 31–58 (1992) |
| [4] | Kapila, A. K. and Ludford, G. S. S. Two-step sequential reactions for large activation energies.Combust. Flame, 29, 167–176 (1977) |
| [5] | Margolis, S. B. and Matkowsky, B. J. Steady and pulsating modes of sequential flame propagation.Comb. Sci. Technol., 27(5-6), 193–213 (1982) |
| [6] | Pel′aez, J. Stability of premixed flames with two thin reaction layers. SIAM J. Appl. Math., 47(4),781–799 (1987) |
| [7] | Golovin, A. A. Matkowsky, B. J. Bayliss, A., and Nepomnyashchy, A. A. Coupled KS-CGL and coupled Burgers-CGL equations for flames governed by a sequential reaction. Physica D, 129,253–298 (1999) |
| [8] | Nepomnyashchy, A. A. Order parameter equations for long wavelength instabilities. Physica D,86, 90–95 (1995)[9] Burgers, J. M. A mathematical model illustrating the theory of turbulence. Adv. Appl. Mech., 1,171–199 (1948) |
| [9] | Burgers, J. M. A mathematical model illustrating the theory of turbulence. Adv. Appl. Mech., 1,171–199 (1948) |
| [10] | Ghidaglia, J. M. and H′eron, B. Dimension of the attractor associated to the Ginzburg-Landau equation. Physica D: Nonlinear Phenomena, 28(3), 282–304 (1987) |
| [11] | Doering, C. R., Gibbon, J. D., Holm, D. D., and Nicolaenko, B. Low-dimensional behavior in the complex Ginzburg-Landau equation. Nonlinearity, 1(2), 279–309 (1988) |
| [12] | Yang, L. E. Guo, B. L., and Xu, H. Y. Inhomogeneous initial boundary value problem for Ginzburg-Landau equations. Appl. Math. Mech. -Engl. Ed., 25(4), 373–380 (2004) DOI10.1007/BF02437520 |
| [13] | Li, D. L. and Guo, B. L. Asymptotic behavior of 2D generalized stochastic Ginzburg-Landau equation with additive noise. Appl. Math. Mech. -Engl. Ed., 30(8), 945–956 (2009) DOI10.1007/s10483-009-0801-x |
| [14] | Li, D. L., Guo, B. L., and Liu, X. H. Regularity of the Attractor for 3-D Complex Ginzburg-Landau Equation. Acta Mathematicae Applicatae Sinica, English Series, 27(2), 289–302 (2011) |
| [15] | Hopf, E. The partial differential equation ut + uux = µuxx. Comm. Pure Appl. Math., 3, 201–230(1950) |
| [16] | Zhu, C. G. and Wang, R. H. Numerical solution of Burgers’ equation by cubic B-spline quasiinterpolation. Appl. Math. Comput.,208, 260–272 (2009) |
| [17] | Chidella, S. R. and Yadav, M. K. Large time asymptotics for solutions to a nonhomogeneous Burgers equation. Appl. Math. Mech. -Engl. Ed., 31(9), 1189–1196 (2010) DOI 10.1007/s10483-010-1352-9 |
| [18] | Friedman, A. Partial Differential Equations, Holt, Rinehart and Winston, New York (1969) |
| [19] | Temam, R. Infinite Dimensional Dynamical Systems in Mechanics and Physics, Springer-Verlag,New York (1997) |
 2013, Vol. 35
2013, Vol. 35









































































































