Article Information
- Zhi-jia LIN,Zhuo ZHUANG. 2014.
- Enriched goal-oriented error estimation for fracture problems solved by continuum-based shell extended finite element method
- Appl. Math. Mech. -Engl. Ed., 35(1): 33-48
- http://dx.doi.org/10.1007/s10483-014-1770-8
Article History
- Received 2013-03-21;
- in final form 2013-06-05
2. ABB (China) Corporate Research Center, Beijing 100084, P. R. China
In recent years,the importance of computer simulations in industrial design has been increased rapidly. Especially,numerical simulation methods for fracture are more and more widely used in research and industrial design since a lot of major disasters originate from a small crack. For example,fracture in pipes has attracted much attention. Much research work[1, 2] based on numerical simulations has been carried out because of the extensive application of pipes in engineering,and the great loss is generally caused by unstable crack propagation. Research caused by similar requirements is also shown in ship building[3],jet engine manufacture[4],polymer industry[5] and so on. Numerical simulation researches have made great contribution to prevent fracture,and significant improvement has been made with the help of experiments. At the same time,verification and validation (V&V) of computational simulations have developed a lot on assessing and quantifying the confidence in astronautics and nuclear industries. The credibility research is playing a more and more important role in many industrial fields. Recently, the extended finite element method (XFEM) has been successfully applied to simulate the dynamic crack propagation,and has a potential as a strong tool for the crack related engineering design. However,the estimation of discretization error bound in simulations of XFEM has rarely been mentioned. In this paper,error estimation of XFEM is discussed to fill this gap and enhance the practical application value of this method.
By using basic analytical solutions as the shape function,XFEM significantly increases the accuracy of fracture simulation. This method was come forward by Belytschko and Black[6] and Moes et al.[7],and excellent applications of it are obtained in various kinds of problems with discontinuity,such as fracture[8, 9],shear band[10],multi-phase flow[11] and so on. The idea of improving shape functions is also applied to the mesh free method for hypervelocity impact simulation[12]. So far,XFEM has been much enhanced in simulations of fracture and other discontinuity problems. The concept of enriched shape functions was drawn into the continuumbased (CB) shell element by Zhuang and Cheng[13] to simulate arbitrary crack growth in the curved shells. The framework of this XFEM process based on CB shell element with 8 nodes can not only simulate shell deformation but also avoid locking problems. However,few works have been dedicated to the computational accuracy of this new kind of 3D XFEM. This verification is necessary for the applications of CB shell XFEM in industries such as aircraft and nuclear plant.
In this study,we extend goal-oriented error estimation from conventional finite element method (FEM) to CB shell XFEM with new freedoms for 3D discontinuity problems in simulations. The equation of energy with enriched freedoms can be described to solve the error bound of CB shell XFEM analysis. The goal-oriented error estimation is established in 1990s by Ainsworth and Oden[14] and Oden and Prudhomme[15]. Ladeveze et al.[16] and Gratsch and Klaus-Jurgen[17] also contribute to the establishment theory. In the goal-oriented error estimation,it focuses on the discretization error of local quantities,which is interested by the designers of simulations. Schleupen and Ramm[18] discussed the concept of error estimation on linear elasto-dynamics. Larsson et al.[19] investigated the methodology and performance of the goal-oriented error estimation for a non-linear elasticity model.
This paper is organized as follows. In section 2,following an introduction of CB shell XFEM analyses in section 2.1,we briefly recall the derivation of goal-oriented error estimation in section 2.2. Then,in section 2.3,we present the concept of our enriched goal-oriented error estimation method against 3D CB shell XFEM and its realization. Results of numerical simulations and comparisons are discussed in section 3,in which both in plane and out of plane tests are carried out. Finally,some conclusions are given in section 4.
2 Methodology 2.1 CB shell XFEMThe theory of CB shell element was first proposed by Ahmad et al.[20] in 1970s,and this method was developed to some nonlinear problems by Nikishkov and Atluri[21] and Hughes and Liu[22]. Such kind of CB shell element represents a kinematical equation for a shell element on a 3D solid element as shown in Fig. 1[23].
The black nodes in Fig. 1 are master nodes which belong to an 8-node shell element in the midsurface. The white nodes are slave nodes which belong to a quadratic solid element. A fiber connects with two slave nodes and one master node together. Therefore,the transition matrix between these two elements can be shown as follows:
 |
| Fig. 1 CB shell element |
By Zhuang and Cheng[24],the enriched shape function of this CB shell element is a sign function. This function in the element crossed by a crack is positive on one side of the crack and negative on the other side. There are two situations when crack goes a cross an element: straight across and with a turning,which are shown in Fig. 2.
 |
| Fig. 2 Two situations for crack crossing element |
(i) Straight crack
In this situation,the CB shell element is intersected by crack ABCD. tc and toc are two vectors which give the direction of crack growing and the crack direction. r is the vector from E to X. s(X) is the sign function defined as
(ii) Crack with twist
In this situation,tc1 and tc2 are direction vectors of the crack growing path. Vector toc denotes the crack direction through the thickness. r is the vector from I to X. Then,s(X) is shown as follows:
Cylinder coordinate is used around the crack tip as shown in Fig. 3. The crack plane is vertical to the θ-plane which is not necessary to be the same plane as the mid-face of element.
 |
| Fig. 3 Crack tip embedded in element |
The enriched shape function ΦJ (X) can be defined as follows with the help of the cylinder coordinate:
where b(X) is a linear combination shown as follows: Since the θ-plane is vertical to the crack,the basis is the same as those in 2D problems. Therefore,the discrete momentum equation with enriched freedoms can be found. 2.2 Goal-oriented error estimationAlthough error estimation along the energy norm gives indication of global error,the identification of some quantity of interest is quite independent. In another word,a small error in the global energy norm does not always guarantee the error being small in local interest quantities, which means that stress or damage should be sufficiently accurate in a critical region. For the problems with some special targets,the error estimation of these special quantities can provide much relevant accurate information for the FEM simulations. In the following,a brief introduction of goal-oriented error estimation is given[14]. The energy balance equation can be written as
where B is the internal energy,and F is the external energy. Then,we define Q as the quantity of interest,which can be any function of u. This original question with a quantity of interest is actually a control function with the energy balance equation as a constraint. The control problem with constraints can be transformed into an extreme-value problem of Lagrange function. With a standard procedure δL = 0,we obtain the dual problem as follows:This equation forms a new relation between the first-order derivative of B and Q. With p being the influence function or Lagrange multiplier,corresponding to the interested quantity,the errors and residuals can be represented in both original and dual problems. Let u0 and p0 represent the FEM approximate solution to these two problems,we have
Then,the error of quantity of interest can be represented with the above residuals. Using Taylor expansion,the residual is simplified as follows:In this way,the first item on the right-side of Eq. (12) can be calculated directly. Therefore, the error of interested quantity is calculated roughly. Then,the bound of this error can be solved by the quadratic term
Since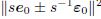 has its own maximum and minimum values,the range of the quadratic
term is estimated.
2.3 Enriched goal-oriented error estimation
has its own maximum and minimum values,the range of the quadratic
term is estimated.
2.3 Enriched goal-oriented error estimation
For XFEM problems,the displacement is formed by two parts of freedoms: u and a. Therefore, the internal and external energy can be written as B(u,a; v,b) and F(v,b) in the same way,respectively. The Lagrange multiplier can also get its enriched form (p,q). Since XFEM is based on the elastic analytical solution of crack,the integral form of B and Q in section 2.2 are linear functions of (u,a) and (p,q),which are,respectively,the solutions of the original and dual problems. The differential form of the dual problem can be represented by an integral form. The original and dual problems are decoupled by
In this condition,(u,a) and (p,q) can be solved separately by Eqs. (15) and (16). In the simulations,the energy balance function is solved with CB shell XFEM. Then,(u0,a0) and (p0,q0) are considered as the discrete solution to the original and dual problems,respectively. On the other hand,the residual of interested quantity is represented as follows:
The original and dual problems need to be overwritten based on the enriched expression of inner product in the energy space. All the forces,displacements,and other quantities have both normal and enriched parts. Corresponding to the enriched displacement field,stress, strain,and nodal force,all of them have to add more freedoms. In this case,the internal and external energies of the discrete form are given by
Based on the enriched goal-oriented error estimation,the residual of original and dual problems can be represented into functions of B and F,respectively. To calculate the residual R, it requirs the discrete solutions to the displacement field (u0,a0) and the influence factor field (p0,q0),respectively. With Eqs. (18) and (19),the goal-oriented error estimation of extended form of XFEM can be carried out. Then,the error bound of XFEM can be calculated without the help from the analytical solution.
As we have described,the enriched goal-oriented error estimation is divided into four steps. Firstly,the original mechanical problem is solved with XFEM. Then,the approximate solution of the displacement field denoted by (u0,a0) can be obtained. Secondly,the quantity of interest can be transferred into an integral function of the displacement field (u,a). After substituting it into the dual problem,the separate weak form of energy can be found on the influence factor (p,q). Thirdly,another XFEM result (p0,q0) is solved as the discrete approximate solution to the dual problem. Finally,the residual distribution can be calculated with (u0,a0) and (p0, q0). After these four steps,the error of the interest quantity can be estimated. The process will be described in detail in the following numerical examples.
3 Numerical resultsA series of numerical tests are calculated with the theoretical models in the previous section. Our aim is to measure the discretization error in CB shell XFEM simulation and use this method to calculate the bound of interested quantity in the fracture analysis. Both stretching and bending tests are designed to verify the computational accuracy. To compare with the results with XFEM simulation,the analytical solutions of the stress intensity factor are used on the edge crack in the finite size plane problem and the center crack in the semi-infinite plane problem. Then,we use the enriched goal-oriented error estimation to solve the error bounds.
3.1 Stretching test 3.1.1 Edge crack modelThe computational example is an 1m×2m rectangular plane with a middle crack on the left edge,as shown in Fig. 4. A tension load σ=1MPa is applied on the top end,and the plane is fixed on the bottom. The length of the crack is changed from 0.15m to 0.45m. The material parameters are Young’s modulus E =30MPa and Poisson’s ratio υ =0.3. The quantity of interest is the stress intensity factor of Mode I crack.
 |
| Fig. 4 Edge crack model |
For this kind of edge crack problems,an analytical solution to Mode I stress intensity factor is given by the elastic fracture mechanics in Eq. (20)[25] as follows:
With this analytical solution,we can solve KI for the edge crack problem while the length of crack grows from 0.15 m to 0.45 m. The results are listed in Table 1 .
The original problem is meshed with 210 CB shell XFEM elements in which 10 elements are distributed along the X-direction. The width of element is 0.1 m.
3.1.2 Extended finite element programAs described in subsection 2.1,XFEM can well solve fracture problems,which takes an extremely advance of accuracy in the fracture simulation. In our XFEM program,the elements include different enrichment ways. For the case that the crack tip is embedded in the element, it is required more enriched freedoms,which is different from the elements crossed by a crack. Since the crack tip combines with the analytical solutions,the crack propagation can be simulated more accurately. On the other hand,a transfer function between solid element and shell element is also contained to take a CB shell simulation. Here,we use the XFEM program developed by ourselves,named Simulation Arbitrary Fracture Analysis Code (SAFRAC)[26, 27]. SAFRAC can simulate crack growth in two-dimensional problems and propagation in threedimensional shells with an arbitrary configuration. The simulation results with SAFRAC are shown in Fig. 5,which illustrates the behavior of an edge crack with its tip in the middle of an element.
 |
| Fig. 5 Simulation of crack tip with SAFRAC (crack tip point is just in middle of an element) |
In fracture problems,the stress intensity factor is a key parameter to represent the attribute of a crack,which results in the criterion with material toughness to evaluate crack propagation or arrest. In this paper,the interested quantity is the stress intensity factor obtained by XFEM simulation. With the help of enriched goal-oriented error estimation,the error bound of this parameter can be computed.
As described in subsection 2.3,based on the mathematical expression of the target function, a dual problem must be established to calculate the influence factor of goal-oriented error estimation. Since we focus on the accuracy of KI,an appropriate relationship between the stress intensity factor and the displacement field must be found.
In Mode I crack,the analytical solution of the displacement field close to the crack tip is given below,i.e.,
With the finite element simulation result,we get KI by displacement extrapolation techniques. This method takes results of a local area around the crack tip to calculate KI. In this area, the result of KI is considered to be linear to the distance between the calculating point and the crack tip. Then,an extrapolation process can be performed to get KI at the crack tip point by the substitution r =0 as shown in Eq. (21) to avoid the numerical singularity. The vertical displacement near the crack tip is used to calculate the stress intensity factor by the extrapolation techniques. The function of KI can be established as where r and θ indicate the polar coordinate relative to the crack tip. Taken two point simulation results in that certain area,KI at r=0 point can be expressed as With Eq. (23),an explicit expression of KI is found. v represents the average value of vertical displacement to a pair of points on both sides of the crack. This process decreases the asymmetry impact in the simulation. The equivalent force in the dual problem is given as follows:The same property of material is used in both original and dual problems to confirm the same expression of internal energy. The external force in the dual problem is the equivalent force in Eq. (24). By XFEM simulation,the influence function p0 is achieved. Next,the simulation results and error estimation are given in the following section.
3.1.4 Error estimation and error bound of KIBoth the original and dual problems are solved with CB shell XFEM. In these simulations, the length of crack is changed from 0.15 m to 0.45 m by an increment of 0.05 m. Taken the case that the crack length is 0.35 m as an example,the stress distribution along the Y -direction of the original problem is solved by SAFRAC,as shown in Fig. 6.
 |
| Fig. 6 σY distribution solved by SAFRAC (stress is component on Y -direction,and width of one element is 0.1 m) |
As seen in Fig. 6,SAFRAC contains a singularity computation and shows the result at the crack tip location accurately. The results of stress intensity factor at the crack tip calculated by the analytical formula and SAFRAC are listed in Table 2 . It can be seen that the results from SAFRAC are always close to the analytical solutions.
In Table 2 ,R is the relative value between the SAFRAC result and the analytical solution. By a dual problem described in subsection 3.1.3,the simulation error of KI is solved by the method in subsection 2.3. This enriched goal-oriented error estimation process provides an implement to evaluate the accuracy of CB shell XFEMsimulation in 2D plane. The error bounds calculated with enriched goal-oriented error estimation are given in Table 3 . The upper and lower bound estimations make a confidence interval to evaluate the error of KI in the SAFRAC simulation,as shown in Fig. 7. This prediction shows that the results of SAFRAC simulation are always close to the analytical solutions. With CB shell XFEM element,SAFRAC gives reliable solutions in stretching problems,no matter where the specific location of the crack tip is in the element. In Table 3 ,All errors in the table are dimensionless by dividing the analytical solution of KI. All errors in Fig. 7 are dimensionless by dividing the analytical solution of KI.
 |
| Fig. 7 Relative error bound of SAFRAC KI by goal-oriented error estimation |
A center crack bending test is chosen as an example to test the performance of enriched goal-oriented error estimation with CB shell XFEM element. This test is a bending problem with a crack in the middle of a plane,as shown in Fig. 8. A pair of bending moments is applied on both sides parallel to the crack. The thickness of the plane is B. The width of the plane is 2b. The length of the crack is 2a.
 |
| Fig. 8 Center crack model |
A standard solution to this center crack problem can be found in Ref. [25] as follows:
where υ means Poisson’s ratio,and f(a/b ) is a shape parameter of the plane which follows a curve shown in the manual.The original problem is meshed by 231 XFEMCB shell elements with 21 elements distributed on the X-direction and 11 elements on the Y -direction. With this model,both the original and dual problems are solved. The quantity of interest is KI in this example.
3.2.2 Calculation of KI in 3D shell simulationThe calculation of the stress intensity factors is based on the work of Nikishkov[21] in 1987. An equivalent domain integral method is established to calculate fracture parameters for 3D cracks. With this method,J,which is the integral of the first and second modes and energy release rate of the third mode of crack can be defined as
For contour integrals,Eqs. (26) and (27) are often used as domain integral equations. To calculate J integrals in different modes,the displacement and stress are separated in three modes[22]. The symmetrical and asymmetrical part of displacement and stress are separated as follows:
where Then,J1 is decomposed into three modes,i.e., In the above equation,GI,GII,and GIII are calculated with the decomposed displacement and stress as follows:As soon as GI,GII,and GIII are integrated,K can be calculated as follows:
whereThe stress intensity factors of the cracks in the shell are different through the thickness according to shell crack theory. Our method just treats them as an average value over shell thickness.
3.2.3 Dual problem of KIIn this test,we still choose KI as the quantity of interest. The extrapolation technique based on the analytical solution of the shell crack is used to get the dual problem. For a shell problem,the displacements near the crack tip are solved analytically by Reissner as follows:
where Ψr and Ψθ are particular rotational freedoms in shell problems,and w is deflection. A1, A2,and D2 are undetermined parameters determined by the actual situation. Here,we use a series of substitutions to simplify the above equations,i.e., Then,the function of KI can be expressed as where z means the location in the thickness direction of the shell. After that,a linear extrapolation process can be performed to get KI at the crack tip point by the substitution r =0. Equation (37) is an explicit expression of KI(Φr,Φθ). With its help,the equivalent forces in dual problem are given as follows:These equivalent forces are actually bending moments in the crack tip coordinate. With a rotation transform as Eq. (39),the equivalent forces we use in the dual problem simulation are constructed as follows:
3.2.4 Error estimation and error bound of KIBoth original and dual problems are solved with CB shell XFEM of SAFRAC. In these simulations,the length of crack is changed from 1m to 2m symmetrically. Take the case that the crack length is 1m as an example. The distribution of the normal stress due to the bending moment is solved by SAFRAC,as shown in Fig. 9.
 |
| Fig. 9 Stress distribution of σx solved by SAFRAC |
As can be seen in Fig. 9,SAFRAC represents a singularity at a crack tip in 3D CB shell XFEM bending simulation. The results of KI at a crack tip calculated by the analytical formula and SAFRAC are listed in Table 4 . It can be seen that the results from SAFRAC fit the analytical solutions of the shell fracture mechanics method well.
By a dual problem as described in subsection 3.2.3,the simulation error of KI can be solved by the enriched goal-oriented error estimation method. This method provides a way to evaluate the accuracy of 3D CB shell XFEM simulation. The error bounds of the bending test in SAFRAC simulation calculated with enriched goal-oriented error estimation are given in Table 5 . All the errors in the table are dimensionless by dividing the analytical solution of KI. The upper and lower bound estimations make an acceptable region to evaluate the error of KI in the simulations as shown in Fig. 10. All the errors in the figure are dimensionless by dividing the analytical solution of KI. The difference of the error ranges in different crack lengths is mainly caused by the distance between the crack tip and the element edge. When the crack tip is close to the element edge,the error of mesh distortion comes into being by integration. This prediction shows that the results of SAFRAC simulation are always similar to the analytical solutions. With CB shell XFEM element,SAFRAC gives reliable solutions in 3D bending problems including cracks in the shell.
 |
| Fig. 10 Relative error bound of SAFRAC KI by goal-oriented error estimation |
In this paper,an enriched error estimation method is developed to evaluate the computation accuracy for 3D CB shell XFEM simulation. This method is improved from goal-oriented error estimation for conventional FEM. A series of new freedoms are extended to fit XFEM,and a transition matrix is used for shell simulation. The error bounds are well estimated by this method. Our process is competent at judging the accuracy of interested quantity in XFEM simulation without analytical solutions or experiment data.
With the help of the enriched goal-oriented error estimation method developed in this paper, the accuracy of CB shell simulation with SAFRAC is judged by both in and out of plane tests. As can be seen in sections 3.1.4 and 3.2.4,this enriched error estimation method can solve the error bound of 3D CB shell simulation precisely. The error range estimation with our method can describe the relationship between numerical error and crack length. Then,we use these results to evaluate CB shell XFEM simulation by SAFRAC code. It is clear that the results of SAFRAC are always close to the analytical solution wherever the crack tip is located in various kinds of loading.
The extensions of this work require the following investigations: with this enriched process, a simulation with some 3D XFEM element which application covers more widely in fracture problems can be verified with this enriched goal-oriented error estimation well. The goaloriented error estimation method can also suitably be applied to problems solved by numerical methods other than FEM. It will be interested in extending this robust error estimation method to some other non-linear problems.
| [1] | Zhuang, Z. and Guo, Y. J. Analysis of dynamic fracture mechanism in gas pipelines. Engineering Fracture Mechanics, 64(3), 271–289 (1999) |
| [2] | Van-Xuan, T. and Samuel, G. Development and industrial applications of X-FEM axisymmetric model for fracture mechanics. Engineering Fracture Mechanics, 82, 135–157 (2012) |
| [3] | Feng, G. Q., Garbatov, Y., and Guedes, S. C. Probabilistic model of the growth of correlated cracks in a stiffened panel. Engineering Fracture Mechanics, 84, 83–95 (2012) |
| [4] | Erice, B., G´alvez, F., Cend´on, D. A., and S´anchez-G´alvez, V. Flow and fracture behavior of FV535 steel at different triaxialities, strain rates and temperatures. Engineering Fracture Mechanics, 79, 1–17 (2012) |
| [5] | Patricia, M. F., Alejandra, F. L., and Federico, R. Nonlinear fracture mechanics of polymers: load separation and normalization methods. Engineering Fracture Mechanics, 79, 389–414 (2012) |
| [6] | Belytschko, T. and Black, T. Elastic crack growth in finite elements with minimal remeshing. International Journal for Numerical Methods in Engineering, 45, 601–620 (1999) |
| [7] | Moes, N., Dolbow, J., and Belytschko, T. A finite element method for crack growth without remeshing. International Journal for Numerical Methods in Engineering, 46, 131–150 (1999) |
| [8] | Moes, N. and Belytschko, T. Extended finite element method for cohesive crack growth. Engineering Fracture Mechanics, 69, 813–833 (2002) |
| [9] | Song, J. H., Areias, P. M. A., and Belytschko, T. A method for dynamic crack and shear band propagation with phantom nodes. International Journal for Numerical Methods in Engineering, 67, 868–893 (2006) |
| [10] | Areias, P. M. A. and Belytschko, T. Two-scale shear band evolution by local partition of unity. International Journal for Numerical Methods in Engineering, 66, 878–910 (2006) |
| [11] | Chessa, J. and Belytschko, T. An extended finite element method for two-phase fluids. Journal of Applied Mechanics, 70(1), 10–17 (2003) |
| [12] | Ma, S., Zhang, X., and Qiu, X. M. Comparison study of MPM and SPH in modeling hypervelocity impact problems. International Journal of Impact Engineering, 36(2), 272–282 (2009) |
| [13] | Zhuang, Z. and Cheng, B. B. A novel enriched CB shell element method for simulating arbitrary crack growth in pipes. Science China: Physics, Mechanics & Astronomy, 54(8), 1520–1531 (2011) |
| [14] | Ainsworth, M. and Oden, J. T. A posteriori error estimation in finite element analysis. Computer Methods in Applied Mechanics and Engineering, 142, 1–88 (1997) |
| [15] | Oden, J. T. and Prudhomme, S. Estimation of modeling error in computational mechanics. Journal of Computational Physics, 182, 496–515 (2002) |
| [16] | Ladeveze, P., Rougeota, P., Blanchardb, P., and Moreaub, J. P. Local error estimators for finite element linear analysis. Computer Methods in Applied Mechanics and Engineering, 176, 231–246 (1999) |
| [17] | Gratsch, T. and Klaus-Jurgen, B. A posteriori error estimation techniques in practical finite element analysis. Computers and Structures, 83, 235–265 (2005) |
| [18] | Schleupen, A. and Ramm, E. Local and global error estimations in linear structural dynamics. Computers and Structures, 76, 741–756 (2000) |
| [19] | Larsson, E., Hansbo, P., and Runesson, K. Strategies for computing goal-oriented a posteriori error measures in non-linear elasticity. International Journal for Numerical Methods in Engineering, 55, 879–894 (2002) |
| [20] | Ahmad, S., Irons, B. B., and Zienkiewicz, O. C. Analysis of thick and thin shell structures by curved finite elements. International Journal for Numerical Methods in Engineering, 2, 419–451 (1970) |
| [21] | Nikishkov, G. P. and Atluri, S. N. An equivalent domain integral method for computing crack-tip integral parameters in nonelastic, thermomechanical fracture. Engineering Fractrure Mechanics, 26, 851–867 (1987) |
| [22] | Hughes, T. J. R. and Liu, W. K. Nonlinear finite element analysis of shells: part 2, three- dimensional shells. Computer Methods in Applied Mechanics and Engineering, 26, 331–362 (1981) |
| [23] | Belytschko, T., Liu, W. K., and Moran, B. Nonlinear Finite Element Method for Continua and Structures, John Wiley & Sons, New York (2000) |
| [24] | Zhuang, Z. and Cheng, B. B. A novel enriched CB shell element method for simulating arbitrary crack growth in pipes. Science China: Physics, Mechanics & Astronomy, 54(8), 1520–1531 (2011) |
| [25] | Qiu, Z. Y. Stress Intensity Factor Manual (in Chinese), Science Press, Beijing (1993) |
| [26] | Zhuang, Z. and Cheng, B. B. Development of XFEM methodology and study on mixed-mode crack propagation. Acta Mechanica Sinica, 27(3), 406–615 (2011) |
| [27] | Zhuang, Z. and Cheng, B. B. Equilibrium state of mode-I sub-interfacial crack growth in bi- materials. International Journal of Fracture, 170(1), 27–36 (2011) |
 2014, Vol. 35
2014, Vol. 35





































