Article Information
- Xiao-jing LIU, Ji-zeng WANG,Xiao-min WANG, You-he ZHOU. 2014.
- Exact solutions of multi-term fractional diffusion-wave equations with Robin type boundary conditions
- Appl. Math. Mech. -Engl. Ed., 35(1): 49–62
- http://dx.doi.org/10.1007/s10483-014-1771-6
Article History
- Received 2013-04-16;
- in final form 2013-08-06
In recent years,considerable interest has been shown in the so-called fractional calculus, which allows us to consider integration and differentiation of any order,not necessarily integer. Such interest has been stimulated by its booming applications in different areas of physics and engineering[1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14],especially as has been pointed out by Nigmatullin[5, 6] that many of the uni- versal electromagnetic,acoustic,and mechanical responses can be modeled accurately by using fractional diffusion-wave equations. A time-fractional diffusion-wave equation can be obtained by replacing the time derivative in the ordinary diffusion-wave equation with a derivative of the fractional order between 0 and 2. The range (0,1) corresponds to the diffusion equation,while the range (1,2) corresponds to the generalized wave equation[15, 16].
Advances in theoretical justifications of the fractional diffusion equations and experimental demonstrations of the ubiquity of anomalous diffusion have led to an intensive effort in recent years to find accurate,stable,and wieldy methods for solutions to fractional diffusion-wave equations[14, 15, 16, 17, 18, 19, 20]. For example,Schneider and Wyss[15] obtained a Green’s function for the frac- tional diffusion-wave equations defined in unbounded or semi-infinite spaces in closed form by using Mellin transforms and Fox H-functions. However,Mainardi[16] thought that the solution method proposed by Schneider and Wyss[15] included too many incomprehensible mathematical theories,which seemed not easy for practical applications. By using a well-known technique, the Laplace transform,Mainardi[16] expressed the Green function in a somewhat different form. Daftardar-Gejji and Bhalekar[17] solved the multi-term fractional diffusion-wave equations by using an iterative Adomian decomposition method. However,such a method depends on the analytical calculation of fractional derivatives of different functions at each iterative step. For the solution to the same equations,Jafari and Seifi[18] adopted the homotopy analysis method and demonstrated a more rapid convergence than the Adomian decomposition method. How- ever,such efficiency in convergence relies on a successful initial guess of the unknown solution, some auxiliary parameters and functions,which usually needs sophisticated mathematical skills. By using the Laplace transform and the finite sine transform technique,Agrawal[7] obtained a general solution being valid for the fractional diffusion-wave equations with homogenous Dirich- let boundary conditions. Daftardar-Gejji and Bhalekar[19] applied the classical separation of a variable method to solve the boundary value problems of the fractional diffusion-wave equa- tions. When the boundary conditions are the Robin type,one usually needs to solve series of transcendental equations numerically to obtain the corresponding eigenvalues,which limits the application of such a method and makes the resulting solution no longer in an exact form. Even for the equations with simple boundary conditions,the solutions obtained by Daftardar-Gejji and Bhalekar[19] have to be expressed in terms of the Mittag-Leffler type functions,which are usually slow to converge and can lead to divergence due to the finite precision of scientific computation,as has been pointed out by Welch et al.[20]. In addition,various numerical tech- niques have also been developed to solve the fractional diffusion-wave equations[21, 22, 23, 24, 25, 26],which include the finite element method[21, 22],the finite difference method[23, 24],and the wavelet method[25, 26],etc. Although these numerical methods can numerically solve broad types of linear and nonlinear fractional problems,analytical solutions are still irreplaceable in serving as benchmarks for justifying numerical and experimental techniques.
Despite the progresses outlined above,the literature on exact solutions to the multi-term time fractional diffusion-wave equations with Robin boundary conditions remains rather scarce due to the general lack of suitable theoretical techniques. Approaches of integral transforms referring to the Fourier and Laplace transforms have been widely used in the solutions to fractional differential equations. However,these approaches are only applicable to equations with infinite or semi-infinite spatial domains. Although the sine transform has been success- fully used by Agrawal[7] for the solutions to fractional differential equations with homogeneous Dirichlet boundary conditions,there are still no appropriate analytical techniques being ap- plicable to fractional diffusion-wave equations with more general boundary conditions. In this paper,we will first develop a method of the integral transform which can transform the frac- tional diffusion-wave equations with Robin boundary conditions into time-fractional ordinary differential equations. With the help of Laplace transform,we can obtain the general exact solutions in the transform domain. In order to analytically obtain the general exact solu- tions to the time fractional diffusion-wave equations in time-space domain,we adopt a special method of the Laplace inversion suggested by Wang et al.[27]. This wavelet-based approach of the Laplace inversion has been justified by successful applications in vibration problems sub- jected to randomness[28, 29, 30] and fractional damping[31, 32]. Finally,we use some examples to demonstrate the application of the proposed analytical method.
2 Laplace inverse transform based on wavelet theoryWang et al.[27] have developed a numerical formula of Laplace inversion based on the scaling transform of Coiflets. The proposed method has been justified to be efficient,robust,and applicable to any reasonable function categories. Based on this method,the inverse function can be expressed as a Coiflets expansion with coefficients approximated by corresponding function samples. It has been proven that the L2-error due to the approximation of the expansion coefficients by the function samples is negligible compared with that due to the projection,as the two types of errors have the same convergence rate[33].
We adopt a special treatment to orthogonal wavelets so that we can express the coefficients in corresponding wavelet expansions exactly by just using the function samplings. For this purpose,we consider the autocorrelation function θ(x) of the Daubechies scaling functions defined as[34, 35]
where Φ(x) is the Daubechies scaling function. The compact support interval of θ(x) is [1 − 2N,2N − 1] when the compact support interval of Φ(x) is [0,2N − 1]. According to the two-scale relation we obtain[34, 35] in which or Table 1 shows the coefficients ak (k = 1,3,5,· · · ,2N − 1) for N = 3,4,and 5.Applying the Fourier transform to Eq. (2),we have
where Noting that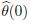 = 1,and applying Eq. (4) recursively,we obtain[36]
= 1,and applying Eq. (4) recursively,we obtain[36]
It is known that  is a low pass filter. Figure 1(a) illustrates the energy spectrums |
is a low pass filter. Figure 1(a) illustrates the energy spectrums | |2
for N=3,4,and 5. As N increases,|
|2
for N=3,4,and 5. As N increases,| |2 approaches the energy spectrum of the ideal low pass
filter. Figure 1(b) shows the difference between |
|2 approaches the energy spectrum of the ideal low pass
filter. Figure 1(b) shows the difference between | |2 and the energy spectrum of the ideal
low pass filter. This difference can be reduced to less than 0.52% within the frequency domain
[0,π/2] and less than 0.01% within the frequency domain [0, 1] when N=5,indicating that
the autocorrelation function θ(x) has a good low pass characteristic for sufficiently large N.
|2 and the energy spectrum of the ideal
low pass filter. This difference can be reduced to less than 0.52% within the frequency domain
[0,π/2] and less than 0.01% within the frequency domain [0, 1] when N=5,indicating that
the autocorrelation function θ(x) has a good low pass characteristic for sufficiently large N.
 |
Fig. 1 Comparison of energy spectrums of | |2 for N = 3,4,5 and ideal low pass filter |2 for N = 3,4,5 and ideal low pass filter |
For a function f(x) ∈ L2(R),we have the following multiresolution decomposition[34, 35, 36, 37]:
in which Let a function f(t) be defined over the interval [0,+∞). The Laplace transform and inversion of f(t) can be defined as where s = β + iω,ω is a real variable,and β is a real constant to insure f(t)e−βt ∈ L2(R). Using the same procedure as developed earlier by Wang et al.[27],we obtain the following exact inversion formula: where As demonstrated by Wang et al.[27],the numerical accuracy of Eq. (11) for the approximation of f(t) depends on the difference between 1 and the energy spectrum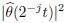 . It can be
seen from Fig. 1 that such a difference is less than 0.01% within domain [0, 1] for N=5 and
resolution level j=0,implying that Eq. (11) can at least give a good approximation to f(t) for
t ∈ [0,2j] by taking into account the dilation effect of resolution level j.
3 Solution to multi-term time-fractional diffusion-wave equation
. It can be
seen from Fig. 1 that such a difference is less than 0.01% within domain [0, 1] for N=5 and
resolution level j=0,implying that Eq. (11) can at least give a good approximation to f(t) for
t ∈ [0,2j] by taking into account the dilation effect of resolution level j.
3 Solution to multi-term time-fractional diffusion-wave equation
By replacing the first or second-order time derivative in a standard diffusion or wave equation with a sum of fractional derivative of order αm ∈ (0,2],we obtain the time-fractional diffusion- wave equation[1, 2, 3, 4, 5, 6, 38, 39],which describes the anomalous diffusion-wave phenomena arising from different circumstances[1, 2, 3, 4, 5, 6, 38, 39]:
where μm,k,a0,b0,al,and bl are constants,q(x,t),gn,u0(t),and ul(t) are known functions, and The unknown function u(x,t) can represent concentration,probability distribution or displace- ment for diffusion,and general transport or wave motion. The fractional derivative operator Dtα is described in the Caputo sense as follows[4]: where f(n)(t) denotes the ordinary derivative of order n,and Γ(x) is the Gamma function. The Laplace transform of the fractional derivative of a function can be formulated as[16] where n − 1 < α ≤ n (n ∈ N).In order to obtain the analytical solution to Eq. (12),we apply the Laplace transform to Eq. (12) to remove the fractional time derivative as follows:
in which and [α] represents the maximal integer less than α. Multiplying both sides of Eq. (15) by e−px and performing integration from 0 to x0 (0≤x0≤l),we can obtain where Setting and taking it as an equation of p,we haveIn the following derivations,we need p1,p2 6= 0. This can be realized by setting β≠Re(s*) for
Inserting p1 and p2 into Eq. (17),respectively,yields From Eq. (21),we further have where x0 is replaced by x,and Applying the Laplace transform to the boundary conditions in Eq. (12),respectively,we have Setting variable x in Eqs. (22a) and (22b) as l,then substituting them into Eq. (24b),we have where From Eqs. (24a) and (25),we can obtain Substituting Eq. (27) into Eq. (22a),we have where Eq. (20) has been considered,andEquation (28) is the exact solution to Eq. (12) in the Laplace domain. This exact solution is valid for Eq. (12) with almost all the classic types of boundary conditions. For example, parameters a0 = al = 0 represent the Dirichlet boundary conditions,b0 = bl = 0 represent the Neumann boundary conditions,and arbitrary values of a0,al,b0,and bl represent the general Robin boundary conditions.
Substituting Eq. (28) into Eqs. (10) and (11),we finally obtain the exact solution to Eq. (12) in the time-space domain as follows:
whereWe note that uj(x,t),as an approximation of u(x,t),almost exactly coincides with u(x,t) for t <2j according to Wang et al.[27].
4 Illustrative examplesExample 1 We consider a non-homogeneous fractional differential equation with the Robin boundary conditions as follows:
By using Eqs. (28) and (29),we have Applying the Laplace inverse transform to Eq. (33),we obtain the exact solution to Eq. (32) as follows: which can be easily verified by substituting Eq. (34) back into Eq. (32). Daftardar-Gejji and Bhalekar[19] applied the separation of variables method to solve the boundary value problems of the fractional diffusion-wave equations with Dirichlet and Neumann boundary conditions, respectively. However,the solution to such an equation with Robin boundary conditions is not considered in their work[19]. Following their procedure,if one uses the separation of variables method to solve the equation with Robin boundary conditions,one must numerically solve the following transcendental equation to get the eigenvalue λ: which is very hard to be solved completely. Only few low order eigenvalues can be obtained numerically,limiting the overall accuracy of the resulting solution.Example 2 As the second example,we consider the following homogeneous fractional dif- ferential equation[19]:
Again using Eq. (28),we have the exact solution in the Laplace domain as follows: Substitute Eq. (37) into Eqs. (30) and (31),the exact solution to Eq. (36) in the time-space domain can be expressed as follows: whereMittag-Leffler type functions[32] have been widely applied to the solution to fractional dif- ferential equations,which satisfy the following relation[32]:
where In terms of Eqs. (40) and (41),Daftardar-Gejji and Bhalekar[19] have also obtained the exact solution to Eq. (36) as follows: However,in practical applications,the Mittag-Leffler functions and their high order derivatives are usually difficult to calculate especially when the time is large,as has been pointed out by Welch et al.[20] and Wang[32].Figure 2 illustrates the comparison of the solutions u(π/2,t) approximated by Eq. (39) for the resolution level j = 6 and by Eq. (42) for different N. It can be seen from Fig. 2 that the result given by Eq. (39) smoothly converges as time increases. In contrary,the result given by Eq. (42) diverges at different time for different N. When N = 250,the convergency range even decreases to [0, 22] due to the finite precision of scientific computation.
Example 3 As the third example,we consider a non-Markovian diffusion process for a particle trapped in a finite space with absorbing-reflecting boundaries and a sharp initial condition[40].
 |
| Fig. 2 Comparison of solutions u(π/2,t) approximated by Eq. (39) for resolution level j = 6 (present)and by Eq. (42) for different N |
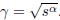 . In addition,the integrated survival probability w(t) in the Laplace transform
domain can be obtained by the integration of Eq. (44) as follows:
. In addition,the integrated survival probability w(t) in the Laplace transform
domain can be obtained by the integration of Eq. (44) as follows:
Thus,exact results on the probability density function p(x,t) and the integrated survival probability w(t) can be obtained by inserting Eqs. (44) and (45) into Eq. (30),respectively.
Figure 3 plots p(x,t) as a function of time and space coordinate in the case of α = 0.75. It can be seen from Fig. 3 that the short-time behavior of the diffusion process is dominated by the initial value: only very small amount of the initial probability released at x = 1/2 has traveled to the absorbing boundary.
 |
| Fig. 3 Probability density function p(x,t) for α = 0.75 |
Figure 4 illustrates the evolution of the probability density p(x,t) at the reflecting boundary x=1 for α = 0.50,0.75,and 1.00. It can be seen from Fig. 4 that,for long time,the slow decay of the sub-diffusion solution in comparison with the Brownian result is obvious. Figure 5 shows the comparison of the integrated survival probability w(t) for α = 0.50,0.75,and 1.00. We can observe from Fig. 5 that a smaller order of fractional derivative corresponds to a longer surviving time. The expected phenomena of sub-diffusion have been discussed in detail by Metzler and Klafter[40].
 |
| Fig. 4 Probability density p(1,t) at reflect- ing boundary for α = 0.50,0.75,and 1.00 |
 |
| Fig. 5 Integrated survival probability w(t) for α = 0.50,0.75,and 1.00 |
In summary,we have proposed a new method of integral transform which can convert the fractional diffusion-wave equations with Robin boundary conditions into time-fractional ordinary differential equations. With the help of Laplace transform,we obtain the general exact solutions in the transform domain. Then,using a modified wavelet-based exact formula of Laplace inverse transform developed earlier by the authors,the resulting exact solutions in the Laplace transform domain are reversed to the space-time domain. This analytical solution method can be easily extended to analyze other linear fractional partial differential equations.
| [1] | Huang, F. H. and Guo, B. L. General solutions to a class of time fractional partial differen- tial equations. Applied Mathematics and Mechanics (English Edition), 31, 815–826 (2010) DOI 10.1007/s10483-010-1316-9 |
| [2] | Mainardi, F. Fractional relaxation-oscillation and fractional diffusion-wave phenomena. Chaos, Solitons & Fractals, 7, 1461–1477 (1996) |
| [3] | Caputo, M. Linear models of dissipation whose Q is almost frequency independent-II. Geophysical Journal of the Royal Astronomical Society, 13, 529–539 (1967) |
| [4] | Caputo, M. and Mainardi, F. Linear models of dissipation in anelastic solids. La Rivista del Nuovo Cimento, 1, 161–198 (1971) |
| [5] | Nigmatullin, R. R. The realization of the generalized transfer equation in a medium with fractal geometry. Physica Status Solidi (B), 133, 425–430 (1986) |
| [6] | Nigmatullin, R. R. To the theoretical explanation of the universal response. Physica B, 123, 739–745 (1984) |
| [7] | Agrawal, O. P. Solution for a fractional diffusion-wave equation defined in a bounded domain. Nonlinear Dynamics, 29, 145–155 (2002) |
| [8] | Chen, W. Time-space fabric underlying anomalous diffusion. Chaos, Solitons & Fractals, 28, 923– 929 (2006) |
| [9] | Chen, W., Sun, H., Zhang, X., and Koroak, D. Anomalous diffusion modeling by fractal and fractional derivatives. Computers and Mathematics with Applications, 59, 1754–1758 (2010) |
| [10] | Chen, W. An intuitive study of fractional derivative modeling and fractional quantum in soft matter. Journal of Vibration and Control, 14, 1651–1657 (2008) |
| [11] | Chen, W. A speculative study of 2/3-order fractional Laplacian modeling of turbulence: some thoughts and conjectures. Chaos, 16, 023126 (2006) |
| [12] | Chen, W. and Holm, S. Modified Szaboo wave equation models for lossy media obeying frequency power law. Journal of the Acoustical Society of America, 114, 2570–2574 (2003) |
| [13] | Chen, W. and Holm, S. Fractional Laplacian time-space models for linear and nonlinear lossy media exhibiting arbitrary frequency dependency. Journal of the Acoustical Society of America, 115, 1424–1430 (2004) |
| [14] | Li, C., Zhang, F., Kurths, J., and Zeng, F. Equivalent system for a multiple-rational-order frac- tional differential system. Philosophical Transactions of the Royal Society A, 371, 20120156 (2013) |
| [15] | Schneider, W. R. and Wyss, W. Fractional diffusion and wave equations. Journal of Mathematical Physics, 30, 134–144 (1989) |
| [16] | Mainardi, F. The fundamental solutions for the fractional diffusion-wave equation. Applied Math- ematics Letters, 9, 23–28 (1996) |
| [17] | Daftardar-Gejji, V. and Bhalekar, S. Solving multi-term linear and non-linear diffusion-wave equa- tions of fractional order by Adomian decomposition method. Applied Mathematics and Computa- tion, 202, 113–120 (2008) |
| [18] | Jafari, H. and Seifi, S. Homotopy analysis method for solving linear and nonlinear fractional diffusion-wave equation. Communications in Nonlinear Science and Numerical Simulation, 14, 2009–2012 (2009) |
| [19] | Daftardar-Gejji, V. and Bhalekar, S. Boundary value problems for multi-term fractional differential equations. Journal of Mathematical Analysis and Applications, 345, 754–765 (2008) |
| [20] | Welch, S. W. J., Ropper, R. A. L., and Duren, R. G. Application of time-based fractional calculus methods to viscoelastic creep and stress relaxation of materials. Mechanics of Time-Dependent Materials, 3, 279–303 (1999) |
| [21] | Ford, N. J., Xiao, J., and Yan, Y. A finite element method for time fractional partial differential equations. Fractional Calculus and Applied Analysis, 14, 454–474 (2011) |
| [22] | Esen, A., Ucar, Y., Yagmurlu, N., and Tasbozan, O. A Galerkin finite element method to solve fractional diffusion and fractional diffusion-wave equations. Mathematical Modelling and Analysis, 18, 260–273 (2013) |
| [23] | Li, C. and Zeng, F. The finite difference methods for fractional ordinary differential equations. Numerical Functional Analysis and Optimization, 34, 149–179 (2013) |
| [24] | Li, C. and Zeng, F. Finite difference methods for fractional differential equations. International Journal of Bifurcation and Chaos, 22, 1230014 (2012) |
| [25] | Zhou, Y. H., Wang, X. M., Wang, J. Z., and Liu, X. J. A wavelet numerical method for solving nonlinear fractional vibration, diffusion and wave equations. Computer Modeling in Engineering and Sciences, 77, 137–160 (2011) |
| [26] | Li, Y. Solving a nonlinear fractional differential equation using Chebyshev wavelets. Communica- tions in Nonlinear Science and Numerical Simulation, 15, 2284–2292 (2010) |
| [27] | Wang, J. Z., Zhou, Y. H., and Gao, H. J. Computation of the Laplace inverse transform by application of the wavelet theory. Communications in Numerical Methods in Engineering, 19, 959–975 (2003) |
| [28] | Koziol, P. and Hryniewicz, Z. Analysis of bending waves in beam on viscoelastic random foun- dation using wavelet technique. International Journal of Solids and Structures, 43, 6965–6977 (2006) |
| [29] | Koziol, P., Mares, C., and Esat, I. Wavelet approach to vibratory analysis of surface due to a load moving in the layer. International Journal of Solids and Structures, 45, 2140–2159 (2008) |
| [30] | Koziol, P., Hryniewicz1, Z., and Mares, C. Wavelet analysis of beam-soil structure response for fast moving train. Journal of Physics: Conference Series, 181, 012052 (2009) |
| [31] | Hong, D. P., Kim, Y. M., and Wang, J. Z. A new approach for the analysis solution of dynamic systems containing fractional derivative. Journal of Mechanical Science and Technology, 20, 658– 667 (2006) |
| [32] | Wang, J. Z. Fractional stochastic description of hinge motions in single protein molecules. Chinese Science Bulletin, 56, 495–501 (2011) |
| [33] | Wei, D. Coiflet-Type Wavelets: Theory, Design, and Applications, Ph. D. dissertation, The Uni- versity of Texas, Austin (1998) |
| [34] | Donoho, D. L. Interpolating Wavelet Transforms, Report, Stanford University, Stanford (1992) |
| [35] | Xu, C. F., Cai, C., Pi, M. H., Zhu, C. X., and Li, G. K. Interpolating wavelet and its applications. Conference of International Symposium on Multispectral Image Process, 3545, 428–432 (1998) |
| [36] | Daubechies, I. Orthonormal bases of compactly supported wavelets. Communications on Pure and Applied Mathematics, 41, 909–996 (1988) |
| [37] | Comincioli, V., Naldi, G., and Scapolla, T. A wavelet-based method for numerical solution of nonlinear evolution equations. Applied Numerical Mathematics, 33, 291–297 (2000) |
| [38] | Metzler, R. and Klafter, J. The random walk’s guide to anomalous diffusion: a fractional dynamics approach. Physics Reports, 339, 1–77 (2000) |
| [39] | Tarasov, V. E. Review of some promising fractional physical models. International Journal of Modern Physics B, 27, 1330005 (2013) |
| [40] | Metzler, R. and Klafter, J. Boundary value problems for fractional diffusion equations. Physica A, 278, 107–125 (2000) |
 2014, Vol. 35
2014, Vol. 35




















































