Article Information
- Chun-xiao GUO, Bo-ling GUO, Hui YANG. 2014.
- H2-regularity random attractors of stochastic non-Newtonian fluids with multiplicative noise
- Appl. Math. Mech. -Engl. Ed., 35(1): 105-116
- http://dx.doi.org/10.1007/s10483-014-1776-7
Article History
- Received 2013-06-03;
- in final form 2013-08-21
2. Institute of Applied Physics and Computational Mathematics, Beijing 100088, P. R. China;
3. College of Mathematics, Yunnan Normal University, Kunming 650500, P. R. China
In this paper,we consider the following stochastic incompressible non-Newtonian fluids with multiplicative noise,and assume that D ⊂ R2 is a two-dimensional bounded smooth open domain,
with the boundary conditions where ◦ denotes the Stratonovich sense in the stochastic term,and ωj(t),1≤j≤m,are mutually independent two-sided Wiener processes,bj ∈ R,1≤j≤m,are given. In Eq. (1), vector function u is the unknown denoting the velocity of the fluid,g is the external force function,and the scalar function π represents the pressure,τij (e(u)) is usually called the extra stress tensor of the fluid, where and τijl = (i,j,l = 1,2),κ = (κ1,κ2) denotes the exterior unit normal to the boundary
∂D. The first condition represents the usual no-slip condition associated with a viscous fluid,
while the second one expresses the fact that the first moments of the traction vanish on ∂D,it
is a direct consequence of the principle of virtual work.
(i,j,l = 1,2),κ = (κ1,κ2) denotes the exterior unit normal to the boundary
∂D. The first condition represents the usual no-slip condition associated with a viscous fluid,
while the second one expresses the fact that the first moments of the traction vanish on ∂D,it
is a direct consequence of the principle of virtual work.
In the case of p = 2,μ1 = bj = 0,Eq. (1) is a deterministic Navier-Stokes equation. In the case of μ0 = μ1 = bj = 0,Eq. (1) is an Euler equation. They both are called Newtonian fluids. The fluid is called shear thinning while 1<p<2 and is shear thickening while p > 2.
There are many works concerning the deterministic non-Newtonian fluids,involving the questions of existence,uniqueness,and regularity of the solution and the existence of attractor and manifold[1, 2, 3, 4, 5, 6, 7].
In the past decades,for stochastic Navier-Stokes equation,Burgers equation,etc.,there have been much work and interesting results,one can refer to Refs. [8, 9, 10, 11, 12, 13, 14],and the references therein. After that,there are a series of papers to investigate stochastic non-Newtonian fluids. Some important results have been obtained,such as Refs. [15, 16, 17, 18] and so on. Recently,Zhao et al.[19] proved the existence of global random attractor for two-dimensional stochastic non-Newtonian fluids with multiplicative noise in the case of 1<p<2,and Guo[20] extended the result to the case of 2<p<3. The operator ∇· (Δe) in Eq. (1) makes the non-Newtonian fluids have a higher four order regularity. For deterministic non-Newtonian fluid system,the H2-regularity attractors have been obtained[3, 5, 21]. We naturally want to know whether the similar result is also true for non-Newtonian fluid with multiplicative noise. That is the reason why the present paper is addressed. In this paper,we prove that there exist H2-regularity random attractors for stochastic non-Newtonian fluids with multiplicative noise in the case of 1<p<2.
The fundamental theory of random dynamical system was developed by Anrold,Crauel, Debussche and Flandoli,and others. They presented a general theory to study random attractor[8, 9]. In this paper,we use the theory to prove the existence of H2-regularity random attractors for stochastic non-Newtonian fluids with multiplicative noise. Firstly,we make use of the Stratonovich transform to change the stochastic equation to a deterministic equation with random parameter. Secondly,we obtain the existence of bounded absorbing sets by some estimates of solution in space V . Thirdly,we use the compact embedding of Sobolev space to obtain the existence of H2-compact random set.
The outline of this paper is as follows. In Section 2,we recall some basic concepts related to random attractors for random dynamical system. In Section 3,we develop all the results needed to prove the existence of random attractors in space V with 1<p<2,g ∈H1. In Section 4,we establish the existence of a compact random attractor in V by compactness of Sobolev embedding.
Remark 1.1 After making the Stratonovich transform,the larger p,the more difficult to obtain some norm estimates of v. Especially,in the case of p > 2,we need to restrict the upper bound of p in order to obtain the existence of H2-compact absorbing set. We should discuss this problem in a forthcoming paper by elaborate estimates.
2 PreliminariesWe introduce some functional spaces and notations for the convenience of the following contents.
Lq(D)—the Lebesgue space with norm ||·||Lq ,and ||·||L2 = ||·||. Particularly,||u||L∞ =
 |u(x)|,for q = ∞.
|u(x)|,for q = ∞.
Hσ(D)—the Sobolev space {u ∈ L2(D),Dku ∈ L2(D),k≤σ},and ||·||Hσ = ||·||σ.
Define a space of smooth functions
H means the closure of V in L2(D) with norm ||·||. The inner product in H denoted by (·,·).
H01 (D) means the closure of V inH1(D) with norm ||·||1.
V means the closure of V in H2(D) with norm ||·||2,and V ′ is the dual space of V .
By simple computation,we can conclude the results ∇·e(u) =  ,and ∇·(Δe(u)) =
,and ∇·(Δe(u)) =  .
Thus,2μ1∇ · (Δe(u)) = μ1Δ2u.
.
Thus,2μ1∇ · (Δe(u)) = μ1Δ2u.
For notational simplicity,C is a generic constant,and may assume various values from line to line throughout this paper.
Consider the positive definite symmetric bilinear form a(·,·) : V × V → R given by
Applying the Lax-Milgram lemma,we obtain an isometric operator A ∈ L(V,V ′) via where V ′ is the dual space of V ,and the domain of A is In fact,A = PΔ2,where P is the Leray projector from L2(D) to H.Define the trilinear form b on H10 (D) ×H10 (D) ×H10 (D) given by
Next,define a bilinear map B onH10 (D) ×H10 (D) by
Define the map N(u) onH10 (D) as follows:
where γ(u) =  .
.
From these preparation,Eqs. (1)-(4) can be translated into the following abstract problems in H:
We recall some basic concepts related to randomattractors for random dynamical system[8, 9]. Let (X,d) be a complete separable metric space with Borel σ-algebra B(x) endowed with distance d,and let (Ω,F,P) be a complete probability space. We also denote mappings S(t,s; ω) : X → X,−∞<s≤t<∞ with explicit dependence on ω.
Definition 2.1 A random set K(t,ω) is called attracting in X,if for any bounded non- random sets B ⊂ X and a.e. ω,
where d(A,B) is the semidistance defined byDefinition 2.2 A family A(ω),ω ∈ of closed subsets of X is said to be measurable,if the mapping ω → d(x,A(ω)) is measurable for each x ∈ X.
Definition 2.3 Let {θt :Ω → Ω,t ∈ R} be a family of measure preserving transformation of (Ω ,F,P) such that θ0 = id and θt+s = θt ◦ θs for all t,s ∈ R. Here,we assume θt is ergodic under P. Especially,for all s<t ∈ R,and x ∈ X,
Definition 2.4 Let S(t,s; ω)t>s,ω∈ be a stochastic dynamical system,if A(t,ω) satisfies:
(1) for any bounded subset B of X,t ∈ R,and a.e. ω ∈ (attracting property),
(2) for a.e. ω ∈ and all s≤t (invariance),
Then,A(t,ω) is called to be the random attractor.Theorem 2.1[8] Let S(t,s; ω)t>s,ω∈ be a stochastic dynamical system satisfying the fol- lowing conditions:
(1) S(t,r; ω)S(r,s; ω)x = S(t,s; ω)x,for all s≤r≤t and x ∈ X;
(2) S(t,s; ω) is continuous in X,for all s≤t;
(3) for all s<t and x ∈ X,the mapping
is measurable from (Ω ,F) to (X,B(X));(4) for all t,x ∈ X and P-a.e. ω,the mapping
is right continuous at any point.Assume that there exists a group θt (t ∈ R) of measure preserving mappings such that
holds and for P-a.e. ω,there exists a compact attracting set K(ω) at time 0,for P-a.e. ω ∈ Ω. We set Λ(ω) = ,where the union is taken over all the bounded subsets of X and
A(B,ω) is given by
Then,Λ(ω) is a random attractor.
,where the union is taken over all the bounded subsets of X and
A(B,ω) is given by
Then,Λ(ω) is a random attractor.
Remark 2.1 In application to stochastic Eqs. (6)-(7),let = {ω ∈ C(R,l2)| ω(0) = 0}, with P being the product measure of two Wiener measures on the negative and the positive time parts of Ω . In this case,time shift θt is defined as
Therefore,the condition (8) is satisfied. 3 A priori estimateIn this section,we introduce an auxiliary Stratonovich process which enables us to change the
stochastic equation to an evolution equation depending on a random parameter. Considering
the process η(t) =  ,which satisfies the Stratonovich equation
,which satisfies the Stratonovich equation
Similarly (see [4, 14]),we can use the Galerkin method to prove that for P-a.e. ω ∈ Ω ,there holds:
i) For g ∈ H,vs ∈ H,s<T ∈ R,there exists a unique weak solution to Eqs. (10)-(11) v ∈ C(s,T ;H)TL2(s,T ; V ) with initial value v(s) = vs.
ii) For g ∈H1,vs ∈ V,s<T ∈ R,there exists a unique weak solution to Eqs. (10)-(11) v ∈ C(s,T ; V )TL2(s,T ;D(A)) with initial value v(s) = vs.
We define the stochastic dynamical system (S(t,s; ω))t>s,ω∈Ω by
The key is to obtain the existence of a compact attracting set at time 0 in V . First,we try to obtain some estimates in H,H1 0 (D),and V . Second,we use the compactness of the embedding to prove the existence of compact random attractors.Lemma 3.1 Let 1<p<2,g ∈ H,there exist random radii r1(ω) and r2(ω),such that ∀ ρ > 0,there exists s(ω)≤−1,such that for all s≤s(ω) and for all us ∈ H with ||us||≤ρ, the solution of Eqs. (10)-(11) with vs = η(s)us satisfies the following inequalities:
where r12(ω) = .
.
Proof Taking the inner product of Eq. (10) with v in H,and noticing that b(u,u,v) = 0, we obtain
Let I = . Applying the condition v = ηu,namely,e(v) =
ηe(u),yields I > 0.
. Applying the condition v = ηu,namely,e(v) =
ηe(u),yields I > 0.
We drop the term involving μ0 in (12),then deduce
where the ǫ-Young inequality is used,and λ is a constant satisfying the inequality ||∇v||2 > λ||v||2. Furthermore,we can get Obviously, For s≤−1,and −1≤t≤0,by the Gronwall lemma on the interval [s,t],we can deduce On the other hand,by standard argument, It follows that σ → eμ1λ2ση2(σ) is pathwise integrable over (−∞,0], Let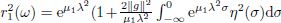 ),which is finite P−a.s. by the above conditions.
Given ρ > 0,there exists s(ω) such that eμ1λ2
η2(s)ρ2≤1,for all s≤s(ω),it follows that
Integrating Eq. (15) with respect to t from [−1,0],we get
we can easily deduce that
),which is finite P−a.s. by the above conditions.
Given ρ > 0,there exists s(ω) such that eμ1λ2
η2(s)ρ2≤1,for all s≤s(ω),it follows that
Integrating Eq. (15) with respect to t from [−1,0],we get
we can easily deduce that
Lemma 3.2 Let 1<p<2,g ∈ H,there exist random radii r3(ω) and r4(ω),such that ∀ ρ > 0,there exists s(ω)≤−1,such that for all s≤s(ω),and for all us ∈ H,with ||u||≤ρ, the solution of Eqs. (10)-(11) with vs = η(s)us satisfies the inequalities
Proof Taking the inner product of Eq. (10) with Δ2v in H,we can get
Obviously,applying the ǫ-Young inequality,we obtain By the H¨older inequality,Gagliardo-Nirenberg inequality,and ǫ-Young inequality,we get where C =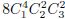 . Similar to the derivation in Ref. [5],we can obtain
Combining the above estimates,we can deduce
It can be also obtained that
Let L(t) =
. Similar to the derivation in Ref. [5],we can obtain
Combining the above estimates,we can deduce
It can be also obtained that
Let L(t) = 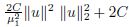 ,M(t) =
,M(t) = 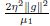 . Then,
For −1≤ξ≤t≤0,using the Gronwall inequality on the interval [ξ,t],we obtain
Integrating the above inequality with respect to ξ over [−1,0],we get
To obtain the boundedness of ||v(t)||2,next,we estimate the right-hand side of inequality (25)
one by one,i.e.,
where we have used the conclusion of Lemma 3.1,
By the property of Stratonovich process η(t) in Lemma 3.1,we deduce that
. Then,
For −1≤ξ≤t≤0,using the Gronwall inequality on the interval [ξ,t],we obtain
Integrating the above inequality with respect to ξ over [−1,0],we get
To obtain the boundedness of ||v(t)||2,next,we estimate the right-hand side of inequality (25)
one by one,i.e.,
where we have used the conclusion of Lemma 3.1,
By the property of Stratonovich process η(t) in Lemma 3.1,we deduce that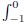 L(σ)dσ and
L(σ)dσ and
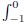 M(σ)dσ are bounded. Combining these estimates,we can conclude that
Integrating (23) with respect to t over [−1,0] ,then
In other words,
M(σ)dσ are bounded. Combining these estimates,we can conclude that
Integrating (23) with respect to t over [−1,0] ,then
In other words,
Actually,from this Lemma,we get
and from the above results,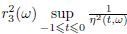 is bounded. This Lemma implies the existence
of bounded absorbing set.
4 Existence of random attractors in V
is bounded. This Lemma implies the existence
of bounded absorbing set.
4 Existence of random attractors in V
In this section,we establish the existence of a compact random attractor in V by compactness of Sobolev embedding. First,we need the following Lemma.
Lemma 4.1 Let 1<p<2,g ∈H1,there exists random radius r7(ω) such that ∀ρ > 0, there exists s(ω)≤−1,satisfying for all s≤s(ω),and for all us ∈ H,with ||us||≤ρ,the solution of Eqs. (10)-(11) with vss = η(s)us satisfies the inequality
Proof Taking the inner product of Eq. (10) with  in H,
in H,
For other nonlinear term,using the H¨older inequality yields
Let The estimate of J is similar to Ref. [15],by the integration by parts,the assumed condition 1<p<2,the Sobolev embedding,and some technological computation. Then,we can get Thus, where we have used the ε-Young inequality,and the condition v = ηu.Putting the above inequalities together,we obtain
Then,changing the inequality suitably to use the Gronwall inequality yields Let Thus, For −1≤ζ≤ξ≤0,by the Gronwall inequality on the interval [ζ,ξ],we obtain Integrating the above inequality with respect to ζ over [−1,0] yields Next,we prove the right-hand side of (33) is bounded. where we have used the conclusion of Lemma 3.2.Note that
where we have used the property of Stratonovich process η(t) and the conclusion of Lemma 3.2.Similarly,
From Eq. (33) and the above inequalities,we obtain Now,we put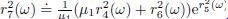 ,especially,for ξ = 0,
,especially,for ξ = 0,
Theorem 4.1 Let 1<p<2,g ∈H1,and us ∈ H,there exist random attractors for the stochastic non-Newtonian fluid with multiplicative noise (6)-(7) in V .
Proof Let K(ω) be the ball in H3(D) with radius r7(ω),we have proved that for any B bounded in V ,there exists s(ω) such that for s≤s(ω),
This clearly implies that K(ω) is an attracting set at time t = 0. Since it is compact in V , Theorem 2.1 applies.Theorem 4.1 implies that the asymptotic smoothing effect of the fluids in the sense that the solution becomes eventually more regular than the initial data.
| [1] | Bellout, H., Bloom, F., and Neˇcas, J. Young measure-valued solutions for non-Newtonian incompressible viscous fluids. Communications in Partial Differential Equations, 19, 1763–1803 (1994) |
| [2] | Bloom, F. Attractors of non-newtonian fluids. J. Dyn. Differ. Equ., 7(1), 109–140 (1995) |
| [3] | Bloom, F. and Hao, W. Regularization of a non-Newtonian system in an unbounded channel: existence of a maximal compact attractor. Nonlinear Analysis: Theory, Methods & Appli- cations, 43, 743–766 (2001) |
| [4] | Guo, B., Lin, G., and Shang, Y. Non-Newtonian Fluids Dynamical Systems (in Chinese), National Defense Industry Press, Beijing (2006) |
| [5] | Zhao, C. and Zhou, S. Pullback attractors for a non-autonomous incompressible non-Newtonian fluid. J. Diff. Equ., 238, 394–425 (2007) |
| [6] | Zhao, C. and Li, Y. A note on the asymptotic smoothing effect of solutions to a non-Newtonian system in 2-D unbounded domains. Nonlinear Analysis, 60, 475–483 (2005) |
| [7] | Guo, B. and Guo, C. The convergence of non-Newtonian fuids to Navier-Stokes equations. J. Math. Anal. Appl., 357, 468–478 (2009) |
| [8] | Crauel, H., Debussche, A., and Flandoli, F. Random attractors. J. Dyn. Differ. Equ., 9, 307–341 (1997) |
| [9] | Crauel, H. and Flandoli, F. Attractors for random dynamical systems. Probality Theory and Related Fields, 100, 365–393 (1994) |
| [10] | Da Prato, G., Debussche, A., and Temam, R. Stochastic Burgers’ equation. Nonlinear Differential Equations and Applications, 1, 389–402 (1994) |
| [11] | De Bouard, A. and Debussche, A. On the stochastic Korteweg-de Vries equation. Journal of Functional Analysis, 154, 215–251 (1998) |
| [12] | De Bouard, A. and Debussche, A. A stochastic nonlinear Schr¨odinger equation with multiplicative noise. Commun. Math. Phys., 205, 161–181 (1999) |
| [13] | Krylov, N. V. and Rozovsikii, B. L. Stochastic evolution equations (in Russian). Journal of Soviet Mathematics, 16, 1233–1277 (1981) |
| [14] | Da Prato, G. and Zabczyk, J. Stochastic Equations in Infinite Dimensions, Cambridge University Press, Cambridge (1992) |
| [15] | Guo, B., Guo, C., and Han, Y. Random attractors of stochastic non-Newtonian fluid. Acta Math. Appl. Sin., 28, 165–180 (2012) |
| [16] | Guo, B., Guo, C., and Zhang, J. Martingale and stationary solutions for stochastic non-Newtonian fluids. Diff. Int. Equ., 23, 303–326 (2010) |
| [17] | Zhao, C. and Duan, J. Random attractor for the Ladyzhenskaya model with additive noise. J. Math. Anal. Appl., 362, 241–251 (2010) |
| [18] | Li, J. and Huang, J. H. Dynamics of 2D Stochastic non-Newtonian fluids driven by fractional Brownian motion, Appl. Math. Mech. -Engl. Ed., 34(2), 189–208 (2013) DOI 10.1007/s10483-013- 1663-6 |
| [19] | Zhao, C., Li, Y., and Zhou, S. Random attractor for a two-dimensional incompressible non- Newtonian fluid with multiplicative noise. Acta Mathematica Scientia, 31, 567–575 (2011) |
| [20] | Guo, C. and Guo, B. Remark on random attractor for a two dimensional incompressible non- Newtonian fluid with multiplicative noise. Commun. Math. Sci., 10, 821–833 (2012) |
| [21] | Zhao, C. and Li, Y. H2-compact attractor for a non-Newtonian system in two-dimensional unbounded domains. Nonlinear Analysis, 56, 1091–1103 (2004) |
 2014, Vol. 35
2014, Vol. 35








































































