Article Information
- Xiang LI, Wei-guo ZHANG, Zheng-ming LI . 2014.
- Shape analysis and damped oscillatory solutions for a class of nonlinear wave equation with quintic term
- Appl. Math. Mech. -Engl. Ed., 35(1): 117-132
- http://dx.doi.org/10.1007/s10483-014-1777-7
Article History
- Received 2013-05-20;
- in final form 2013-09-11
2. College of Science, University of Shanghai for Science and Technology, Shanghai 200093, P. R. China
A class of nonlinear wave equation with a quintic term
includes many important models in applied mathematics and mechanics.If γ = 0 and a5 = 0,Eq. (1) becomes the Klein-Gordon equation[1]
which describes relativistic electrons. Wazwaz[2],Sirendaoreji[3],Jang[4],and Ye and Zhang[5] have studied the compactons,solitons,and solitary wave solutions.If a5 = 0,Eq. (1) becomes nonlinear telegraph equation[6]
Equation (3) also can describe the pressure produced by pulsation when the blood flows in arterial. Many results on it can be seen in Refs. [7, 8, 9, 10]. To speak of Ref. [10],the relation between the shape of solitary wave solution for Eq. (3) and the dissipation effect was analyzed by the theory and method of planar dynamic systems. In some ways,this paper can be regarded as an extent of Ref. [10]. The interaction of a higher-order term (quintic term) and a dissipation term will make the traveling wave solutions of Eq. (1) more complex. We have seen little literature on this point so far. This is also the gist of our paper.If γ = 0,Eq. (1) becomes
Equation (4) can be regarded as the approximate equation of and because sin u and sinh u can be approached by the polynomials of odd number power about u. References [11, 12, 13, 14] investigated the solitary wave solutions of Eq. (4). In Ref. [15],Li and Zhang analyzed the bifurcations of traveling wave solutions for Eq. (4),and obtained all of its explicit solitary wave solutions and kink wave solutions by bifurcation theory of planar dynamical systems. Recently,the theory and method of planar dynamical systems have been developed and widely used to study the traveling wave solutions of integral systems with singular lines. Many good results have been obtained in Refs. [16, 17]. As far as we know,dissipation is inevitable in practical problem. Therefore,it is necessary to study the case of ≠ 0. If ≠ 0,Eq. (1) can be regarded as the approximate equation of Eqs. (5) and (6),which is accompanied by a damping term. Since Eqs. (5) and (6) are very important in mechanics and particle physics,it is meaningful to study Eq. (1).Making a general survey to the previous references,we find that they all obtained some solutions purely,without giving us the global structure for the traveling wave solutions of Eq. (1). Inspired by Refs. [15, 16, 17],we employ the method of planar dynamical systems to study the dissipative system corresponding to Eq. (1),and give the global phase portraits. Then,we use these global phase portraits to study the shapes and existent number of all bounded traveling wave solutions. Next,we discuss the relation between the shapes of bounded traveling wave solutions and dissipation coefficient γ ,and obtain two critical values which can characterize the scale of the dissipation effect. It can be proved that when the dissipation effect is large,the bounded traveling wave solutions of Eq. (1) appear as the kink solitary wave solutions; when it is small,they appear as the damped oscillatory solutions. By using the undetermined coefficients method,we find out the bounded traveling wave solutions of Eq. (1),including exact bell and kink profile solitary wave solutions and approximate damped oscillatory solutions. Furthermore,by using the homogenization principle,we will give the error estimates for the approximate damped oscillatory solutions by establishing the integral equations which reflects the relation between exact solutions and approximate solutions.
The organization of this paper is as follows. In Section 2,we make a qualitative analysis of the dynamical system which the traveling wave solutions of Eq. (1) correspond to. In Section 3,we study the dissipation effect on the shape of bounded traveling wave solutions. In Section 4,we present the bounded traveling wave solutions of Eq. (1),including exact bell and kink profile solitary wave solutions and approximate damped oscillatory solutions. In Section 5,we give the error estimate for approximate damped oscillatory solutions obtained in previous sections.
2 Qualitative analysis to corresponding planar dynamical systemAssume that Eq. (1) has the traveling wave solution in the form of u(x,t) = u(ξ) = u(x−ct),where c is the wave speed. Thus,Eq. (1) satisfies
Not loss generality,we suppose c2 − β > 0.Let x = u(ξ),y = uξ(ξ). Then,Eq. (1) can be converted into the following planar dynamical system:
where r = −cγ . We assume r ≤ 0. For the case of r > 0,it can be discussed similarly.Denote  Thus,the number of singular points for system (8) can be determined by the number of real roots of f(x). Denote Δ = a23 − 4a1a5. Equation (1) has bounded traveling wave solutions only when f(x) at least has two real roots. Therefore,we suppose Δ > 0. Denote x1 =
Thus,the number of singular points for system (8) can be determined by the number of real roots of f(x). Denote Δ = a23 − 4a1a5. Equation (1) has bounded traveling wave solutions only when f(x) at least has two real roots. Therefore,we suppose Δ > 0. Denote x1 =  ,x2 =
,x2 =  ,and x3 =
,and x3 =  . The possible cases are listed as follows.
. The possible cases are listed as follows.
(i) If a1 < 0,Δ > 0,and x2 < 0 < x1,f(x) has three different real roots,where x0 = 0 and x1± = ±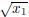 .
.
(ii) If a1 > 0 and a3 < 0,(a) if Δ > 0,0 < x2 < x1,f(x) has five different real roots,where x0 = 0,x1± = ±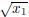 ,and x2± = ±
,and x2± = ± ; (b) if Δ = 0,x3 > 0,f(x) has three different real roots,where x0 = 0 and x3± = ±
; (b) if Δ = 0,x3 > 0,f(x) has three different real roots,where x0 = 0 and x3± = ± .
.
Denote the Jacobian matrices of system (8) at P0(0,0) and Pi±(xi±,0) as
For the sake of discussion,we let Δ0 = r2 − 4a1(c2 − β) and Δi = r2 − 4(c2 − β)(5a5x2i + 3a3xi + a1),i = 1,2,3.
We apply the theory and method of planar dynamical systems[18, 19] to make a qualitative analysis for system (8) from three aspects (finite singular points,infinite singular points,and existence of limit cycle).
2.1 Types of finite singular points for system (8)(I) In the case of r = 0.
At this time,system (8) has the first integral
Through analysis,we know that P0 is a saddle point if a1 < 0 and a center if a1 > 0. The types of Pi±,i = 1,2,3,are listed as follows.(i) a1 < 0. System (8) has three different finite singular points: P0(0,0) and P1±(x1±,0). Since f′(x1±) > 0 and Eq. (9) holds,P1±(x1±,0) are centers.
(ii) a1 > 0 and a3 < 0. (a) If Δ > 0,system (8) has five finite singular points: P0(0,0),P1±(x1±,0),and P2±(x2±,0). Since f′(x1±) > 0 and (9) holds,P1±(x1±,0) are centers. Since f′(x2±) < 0,both P2±(x2±,0) are saddle points. (b) If Δ = 0,system (8) has three finite singular points: P0(0,0) and P3±(x3±,0). Since f′(x3±) = 0 and the Poincar´e index is 0,both P3±(x3±,0) are cusps.
(II) In the case of r < 0.
P0 is a saddle point if a1 < 0. If a1 > 0 and Δ0 > 0,P0 is an unstable node point; if a1 > 0 and Δ0 < 0,P0 is an unstable focus point. The types of other singular points are listed as follows.
(i) a1 < 0. System (8) has three different finite singular points: P0(0,0) and P1±(x1±,0). Since f′(x1±) > 0 ,P1±(x1±,0) are unstable node points if Δ1 > 0; while P1±(x1±,0) are unstable focus points if Δ1 < 0.
(ii) a1 > 0 and a3 < 0. (a) If Δ > 0,system (8) has five finite singular points: P0(0,0),P1±(x1±,0),and P2±(x2±,0). Since f′(x1±) > 0,P1±(x1±,0) are unstable focus points if Δ1 < 0 and unstable node points if Δ1 > 0. Since f′(x2±) < 0,both P2±(x2±,0) are saddle points; (b) If Δ = 0,system (8) has three finite singular points: P0(0,0) and P3±(x3±,0). It is easy to prove that both P3±(x3±,0) are saddle-node points.
2.2 Types of infinite singular points for system (8)We use Poincar´e transformation to analyze the singular points at infinity of system (8). It is easy to know that there exists a couple of singular points at infinity on the y-axis which are denoted by A1 and A2,respectively. There exists a hyperbolic type region around Ai,i = 1,2,respectively. Moreover,the circumference of Poincar´e disk is orbits.
2.3 Existence of limit cycle for system (8)Since  ,for system (8) and the Bendixson-Dulac criterion,we can have the following proposition.
,for system (8) and the Bendixson-Dulac criterion,we can have the following proposition.
Proposition 1 If r ≠ 0,system (8) does not have any closed orbit or singular closed orbit on (x,y) phase plane. This shows that Eq. (1) has neither periodic traveling wave solution nor bell profile solitary wave solution as r ≠ 0.
2.4 Global phase portraits of system (8)Furthermore,based on the above qualitative analysis,we present all possible global phase portraits for system (8) in the case of r = 0 and r < 0 (see Figs. 1-6).
(i) The global phase portrait in the case of r = 0 (see Figs. 1-3).
 |
| Fig. 1 Global phase portrait with a1 < 0 (r=0) |
 |
| Fig. 2 Global phase portrait with a1 > 0,a − 3 < 0,and Δ = 0 (r=0) |
 |
| Fig. 3 Global phase portrait with a1 > 0,a − 3 < 0,and Δ > 0 (r=0) |
(ii) The global phase portrait in the case of r < 0 (see Figs. 4-6).
We take the case in Fig. 4(a) for example to explain how to establish the global phase portraits. Based on the results in the previous qualitative analysis,we know that the key step to determine the global structure of the orbit is to determine the directions and relative position of the separatrix for saddle point P0(0,0). Obviously,x = 0 and y = 0 are not the orbits of system (8). Therefore,there must exist an angle between the separatrix and coordinate axis. From ,we know that x increases as ξ increases when y > 0 while decreases as ξ increases when y < 0. The directions of separatrix are shown in Fig. 4(a).
,we know that x increases as ξ increases when y > 0 while decreases as ξ increases when y < 0. The directions of separatrix are shown in Fig. 4(a).
 |
| Fig. 4 Global phase portrait with a1 < 0 (r < 0) |
 |
| Fig. 5 Global phase portrait with a1 > 0,a3 < 0,and Δ = 0 (r < 0) |
 |
| Fig. 6 Global phase portrait with a1 > 0,a3 < 0,and Δ > 0 (r < 0) |
Secondly,we determine the relative position of the separatrix. We know from subsection 2.2 that there is a hyperbolic type region around infinite singular points Ai,i = 1,2. This means that Ai,i = 1,2,are neither source points nor sink points; moreover,there is no orbit entering or exiting from Ai,i = 1,2. Meanwhile,P1±(0,0) are unstable node points. Therefore,the separatrix away from saddle point P0(0,0) in the forward direction can neither approach to unstable mode points P1±(0,0) nor infinite. And the separatrix entering saddle point P0(0,0) in the forward direction can only come from P1±(0,0). Thus,all directions of the orbits are determined (see Fig. 4(a)). Other global phase portraits can be established in the same way.
From Figs. 1-6,we have the following proposition.
Proposition 2 Except singular points P0 and Pi,i = 1,2,3,and orbits L(P0,Pi±),i = 1,2,3,and L(P1±,P2±),the non-periodic solutions of system (8) are unbounded. Moreover,the coordinate values of the points on these orbits tend to infinite.
2.5 Existence of bounded traveling wave solutionsIt is well-known that a homoclinic orbit of planar dynamical system corresponds to a bell profile solitary wave solution of its corresponding nonlinear evolution equation; the heteroclinic orbit corresponds to a kink profile solitary or an oscillatory wave solution; the closed orbit corresponds to a periodic wave solution. Then,we can derive the following theorem from Figs. 1-6 and Proposition 2.
Theorem 1 (i) If r = 0,Eq. (1) at most has two bounded traveling wave solutions. Two bell profile solitary traveling wave solutions correspond to the homoclinic orbits L(P0,P0) in Fig. 1 or L(P2±,P2±) in Fig. 3; or two kink profile solitary traveling wave solutions correspond to the heteroclinic orbits L(P2±,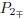 ) in Fig. 2 or L(P2±,
) in Fig. 2 or L(P2±,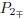 ) in Fig. 3.
) in Fig. 3.
(ii) If r < 0,Eq. (1) at most has four bounded traveling wave solutions. Four kink pro- file solitary wave solutions correspond to the heteroclinic orbits L(P1±,P2±) and L(P0,P2±) in Fig. 6(a); or four oscillatory traveling wave solutions correspond to the heteroclinic orbits L(P1±,P2±) and L(P0,P2±) in Fig. 6(d); or two kink profile solitary wave solutions correspond to the heteroclinic orbits L(P0,P2±) in Fig. 6(b) or L(P1±,P2±) in Fig. 6(c),and two oscilla- tory traveling wave solutions correspond to the heteroclinic orbits L(P1±,P2±) in Fig. 6(b) or L(P0,P2±) in Fig. 6(c).
3 Relation between shapes of bounded traveling wave solutions for Eq. (1) and dissipation coefficient γTheorem 2 Suppose a1 < 0. Then,we have the following results:
(i) If |γ | >  ,Eq. (1) has a monotone decreasing kink profile solitary wave solution u(ξ),satisfying u(−∞) =
,Eq. (1) has a monotone decreasing kink profile solitary wave solution u(ξ),satisfying u(−∞) = 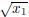 and u(+∞) = 0; and a monotone increasing kink profile solitary wave solution satisfying u(−∞) = −
and u(+∞) = 0; and a monotone increasing kink profile solitary wave solution satisfying u(−∞) = −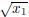 and u(+∞) = 0. Here,u(ξ) corresponds to the orbits L(P1±,P0) in Fig. 4(a).
and u(+∞) = 0. Here,u(ξ) corresponds to the orbits L(P1±,P0) in Fig. 4(a).
(ii) If |γ | <  ,Eq. (1) has two damped oscillatory traveling wave solutions u(ξ),satisfying u(−∞) =
,Eq. (1) has two damped oscillatory traveling wave solutions u(ξ),satisfying u(−∞) = 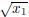 ,u(+∞) = 0,and u(−∞) = −
,u(+∞) = 0,and u(−∞) = −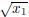 ,u(+∞) = 0,respectively. Here,u(ξ) corresponds to the orbits L(P1±,P0) in Fig. 4(b).
,u(+∞) = 0,respectively. Here,u(ξ) corresponds to the orbits L(P1±,P0) in Fig. 4(b).
Proof (i) From the theory of planar dynamical systems,we know that P1± are unstable node points if Δ1 > 0,i.e.,Δ1 = r2 −4(c2 −β)(5a5x21+3a3x1 +a1) > 0. Since x1 also satisfies a5x21 + a3x1 + a1 = 0 and r = −c ,we have |γ | >  . Meanwhile,P0 is a saddle point. There exists an orbit L(P1+,P0) in {(x,y)|x > 0,−∞ < y < +∞} and an orbit L(P1-,P0) in {(x,y)|x < 0,−∞ < y < +∞} for system (2).
. Meanwhile,P0 is a saddle point. There exists an orbit L(P1+,P0) in {(x,y)|x > 0,−∞ < y < +∞} and an orbit L(P1-,P0) in {(x,y)|x < 0,−∞ < y < +∞} for system (2).
Next,we prove that the kink profile solitary wave solutions are monotone if |γ | >  . From the relation between the traveling wave solutions and the orbits,we only need to prove the exact position of the orbits when |γ | >
. From the relation between the traveling wave solutions and the orbits,we only need to prove the exact position of the orbits when |γ | >  .
.
Since system (2) is symmetrical about the origin,we just need to study the relation be- tween the shape of the bounded traveling wave solution corresponding to L(P1+,P0) and the dissipation coefficient . Denote k1,2 =  . Since |γ | >
. Since |γ | >  ,there exists k0 ∈ (k1,k2) such that 4(c2 −β)
,there exists k0 ∈ (k1,k2) such that 4(c2 −β)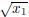 k20 −cγk0 +a5
k20 −cγk0 +a5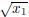 (x1 − x3) < 0 holds. Further,we have
(x1 − x3) < 0 holds. Further,we have  > 2k0
> 2k0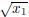 . Denote the curve l as y = k0(x2 −x1). Then,there is a closed region AP0P1+ inside l,x-axis,and y-axis (see Fig. 7).
. Denote the curve l as y = k0(x2 −x1). Then,there is a closed region AP0P1+ inside l,x-axis,and y-axis (see Fig. 7).
Substitute the coordinate values of the point on the arc  1+,segment P0P1+,and P0A into system (8),respectively. We have
1+,segment P0P1+,and P0A into system (8),respectively. We have
 |
Fig. 7 Tangent slope on  1+,P0P1+,and P0A 1+,P0P1+,and P0A |
Since  = ∞ and
= ∞ and  > 0,the tangent slope on the arc
> 0,the tangent slope on the arc 1+,segment P0P1+,and P0A are shown in Fig. 7. Obviously,the region closed by
1+,segment P0P1+,and P0A are shown in Fig. 7. Obviously,the region closed by 1+,P0P1+,and P0A is generalized non-tangential. That is to say L(P1+,P0) cannot pass through the closed region AP0P1+. Actually,if L(P1+,P0) passes through the closed region AP0P1+,it cannot penetrate into the closed region AP0P1+ again. Otherwise,there must exits a direction,which is tangent to
1+,P0P1+,and P0A is generalized non-tangential. That is to say L(P1+,P0) cannot pass through the closed region AP0P1+. Actually,if L(P1+,P0) passes through the closed region AP0P1+,it cannot penetrate into the closed region AP0P1+ again. Otherwise,there must exits a direction,which is tangent to 1+,or P0P1+,or P0A,because of the direction changing continuously in vector field. This is contradictory with the generalized non-tangential. Therefore,L(P1+,P0) cannot pass through the closed region AP0P1+. From the symmetry of system (8) about the origin,the orbit L(P1-,P0) can satisfy the similarly condition. Therefore,the orbits L(P1+,P0) are shown as Fig. 4(a).
1+,or P0P1+,or P0A,because of the direction changing continuously in vector field. This is contradictory with the generalized non-tangential. Therefore,L(P1+,P0) cannot pass through the closed region AP0P1+. From the symmetry of system (8) about the origin,the orbit L(P1-,P0) can satisfy the similarly condition. Therefore,the orbits L(P1+,P0) are shown as Fig. 4(a).
The above proof also reflects the correctness of the global phase portraits in Fig. 4(a).
From the relation between the traveling wave solutions and the orbits,we have that the kink profile solitary wave solution u(ξ) corresponding to L(P1+,P0) (L(P1-,P0)) satisfies y = u′(ξ) < 0 (y = u′(ξ) > 0). Thus,it is monotone decreasing (increasing).
(ii) From the theory of planar dynamical systems,we know that P1± are unstable focus points if Δ1 < 0,i.e.,|γ | <  and P0 is a saddle point. There exists an orbit L(P1+,P0) in {(x,y)|x > 0,−∞ < y < +∞} and an orbit L(P1-,P0) in {(x,y)|x < 0,−∞ < y < +∞} for system (8). Hence,from the relation between Eq. (1) and system (8),we can derive that Eq. (1) has two damped oscillatory traveling wave solutions.
and P0 is a saddle point. There exists an orbit L(P1+,P0) in {(x,y)|x > 0,−∞ < y < +∞} and an orbit L(P1-,P0) in {(x,y)|x < 0,−∞ < y < +∞} for system (8). Hence,from the relation between Eq. (1) and system (8),we can derive that Eq. (1) has two damped oscillatory traveling wave solutions.
The shape of damped oscillatory traveling wave solutions for Eq. (1) described in Theorem2 can be expressed by Fig. 8.
Similarly,we can prove the following theorems.
Theorem 3 Suppose a1 > 0,a3 < 0,and a23 − 4a1a5 = 0,we have the following results:
(i) If |γ | >  ,Eq. (1) has a monotone increasing kink profile solitary wave solution u(ξ) satisfying u(−∞) = 0 and u(+∞) =
,Eq. (1) has a monotone increasing kink profile solitary wave solution u(ξ) satisfying u(−∞) = 0 and u(+∞) =  and a monotone decreasing kink profile solitary wave solution satisfying u(−∞) = 0 and u(+∞) = −
and a monotone decreasing kink profile solitary wave solution satisfying u(−∞) = 0 and u(+∞) = − . Here,u(ξ) corresponds to the orbits L(P0,P3±) in Fig. 5(a).
. Here,u(ξ) corresponds to the orbits L(P0,P3±) in Fig. 5(a).
 |
| Fig. 8 Shape of damped oscillatory traveling wave solutions |
(ii) If |γ | <  ,Eq. (1) has two damped oscillatory traveling wave solutions u(ξ) satisfying u(−∞) = 0,u(+∞) =
,Eq. (1) has two damped oscillatory traveling wave solutions u(ξ) satisfying u(−∞) = 0,u(+∞) =  and u(−∞) = 0,u(+∞) = −
and u(−∞) = 0,u(+∞) = − ,respectively. Here,u(ξ) corresponds to the orbits L(P0,P3±) in Fig. 5(b).
,respectively. Here,u(ξ) corresponds to the orbits L(P0,P3±) in Fig. 5(b).
Theorem 4 Suppose a1 > 0,a3 < 0,and a23 − 4a1a5 > 0. Then,we have the following results:
(i) If |γ | >  ,Eq. (1) has a monotone decreasing kink profile solitary wave solution u(ξ) satisfying u(−∞) =
,Eq. (1) has a monotone decreasing kink profile solitary wave solution u(ξ) satisfying u(−∞) = 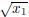 and u(+∞) =
and u(+∞) =  and a monotone increasing kink profile solitary wave solution satisfying u(−∞) = −
and a monotone increasing kink profile solitary wave solution satisfying u(−∞) = −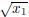 and u(+∞) = −
and u(+∞) = − . Here,u(ξ) corresponds to the orbits L(P1±,P2±) in Fig. 6(a) or Fig. 6(c).
. Here,u(ξ) corresponds to the orbits L(P1±,P2±) in Fig. 6(a) or Fig. 6(c).
(ii) If |γ | <  ,Eq. (1) has two damped oscillatory traveling wave solu- tions u(ξ) satisfying u(−∞) =
,Eq. (1) has two damped oscillatory traveling wave solu- tions u(ξ) satisfying u(−∞) = 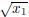 ,u(+∞) =
,u(+∞) =  and u(−∞) = −
and u(−∞) = −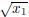 ,u(+∞) = −
,u(+∞) = − ,respectively. Here,u(ξ) corresponds to the orbits L(P1±,P2±) in Fig. 6(b) or Fig. 6(d).
,respectively. Here,u(ξ) corresponds to the orbits L(P1±,P2±) in Fig. 6(b) or Fig. 6(d).
(iii) If |γ | >  ,Eq. (1) has a monotone increasing kink profile solitary wave solution u(ξ) satisfying u(−∞) = 0,u(+∞) =
,Eq. (1) has a monotone increasing kink profile solitary wave solution u(ξ) satisfying u(−∞) = 0,u(+∞) =  and a monotone decreasing kink profile solitary wave solution satisfying u(−∞) = 0,u(+∞) = −
and a monotone decreasing kink profile solitary wave solution satisfying u(−∞) = 0,u(+∞) = − . Here,u(ξ) corresponds to the orbits L(P0,P2±) in Fig. 6(a) or Fig. 6(b).
. Here,u(ξ) corresponds to the orbits L(P0,P2±) in Fig. 6(a) or Fig. 6(b).
(iv) If |γ | <  ,Eq. (1) has two damped oscillatory traveling wave solutions u(ξ) satisfying u(−∞) = 0,u(+∞) =
,Eq. (1) has two damped oscillatory traveling wave solutions u(ξ) satisfying u(−∞) = 0,u(+∞) =  and u(−∞) = 0,u(+∞) = −
and u(−∞) = 0,u(+∞) = − ,respectively. Here,u(ξ) corresponds to the orbits L(P0,P2±) in Fig. 6(c) or Fig. 6(d).
,respectively. Here,u(ξ) corresponds to the orbits L(P0,P2±) in Fig. 6(c) or Fig. 6(d).
In light of Ref. [9],we suppose that Eq. (1) has the bell profile solitary solutions in the form
Substitution of Eq. (10) into Eq. (7) yields the following theorem.Theorem 5 If γ = 0 and a1 < 0,Eq. (1) has two bell profile solitary wave solutions u1± (ξ) = ± 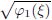 ,where
,where
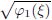 correspond to two symmetrical homoclinic orbits L(P0,P0) in Fig. 1.
correspond to two symmetrical homoclinic orbits L(P0,P0) in Fig. 1.
Remark 1 We can verify that Eq. (11) is equivalent to Eq. (45) in Ref. [11] and Eq. (11) in Ref. [12].
Obviously,the asymptotic values of solutions u1± (ξ) are zero. While the solutions,whose asymptotic value are not zero,are listed as follows.
We suppose that Eq. (1) has the bell profile solitary solutions in the form
Substitution of Eq. (12) into Eq. (7) yields the following theorem.Theorem 6 If γ = 0,Eq. (1) has two bell profile solitary wave solutions u2± (ξ) = ± 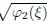 ,where
,where
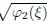 correspond to two symmetrical homoclinic orbits L(P2±,P2±) in Fig. 3.
4.2 Kink profile solitary solutions of Eq. (1)
correspond to two symmetrical homoclinic orbits L(P2±,P2±) in Fig. 3.
4.2 Kink profile solitary solutions of Eq. (1)
To obtain the kink profile solitary wave solutions of Eq. (1) when γ = 0,we suppose that they are in the form
Substituting Eq. (14) into Eq. (7) and computing it by MAPLE,we have the following theorem.Theorem 7 If γ = 0,Eq. (1) has two kink profile solitary wave solutions,
Here,u3± (ξ) correspond to the heteroclinic orbits L(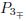 ,P3±) in Fig. 2 orL(
,P3±) in Fig. 2 orL(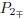 ,P2±) in Fig. 3.
,P2±) in Fig. 3.
To obtain the kink profile solitary wave solutions of Eq. (1) when ≠ 0,we suppose that they are in the form
Substituting (16) into (7) and computing it by MAPLE,we have the following theorems.Theorem 8 If a1 < 0 and γ2 =  ,Eq. (1) has two kink profile solitary wave solutions,
,Eq. (1) has two kink profile solitary wave solutions,
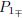 ) in Fig. 4(a).
) in Fig. 4(a).
Theorem 9 If a1 > 0 and γ2 =  ,Eq. (1) has two kink profile solitary wave solutions,
,Eq. (1) has two kink profile solitary wave solutions,
In this part,we give the approximate expressions of damped oscillatory solutions for Eq. (1) according to their structures (see Fig. 8). We take the damped oscillatory solution corresponding to the focus-saddle orbit L(P1+,P0) in Fig. 4(b) for example,while other cases can be studied similarly. By the rotation vector field theory in planar dynamical systems,it is easy to see that the focus-saddle orbit L(P1+,P0) in Fig. 4(b) comes from the break of the left homoclinic orbit L(P0,P0) in Fig. 2 under the effect of dissipation term γut (the dissipation coefficient γ satisfies |γ | <  ). Hence,the non-oscillatory part of the damped oscillatory solution corresponding to L(P1+,P0) can be expressed by the bell profile solitary wave solution in Theorem 5 as follows:
). Hence,the non-oscillatory part of the damped oscillatory solution corresponding to L(P1+,P0) can be expressed by the bell profile solitary wave solution in Theorem 5 as follows:
We use the form
to approximatively express the oscillatory part of this damped oscillatory solution,where A1,A2,B,C,and α are undetermined constants. The reason why we choose Eq. (20) is that it has both damped and oscillatory properties. eα(ξ−ξ0) has damped property while A1 cos(B(ξ − ξ0)) − A2 sin(B(ξ − ξ0)) has oscillatory property.Substituting Eq. (20) into Eq. (7),and neglecting the terms including O(eα(ξ−ξ0)),we have
In order to derive the approximate damped oscillatory solution of Eq. (1),there still requires some conditions to connect Eqs. (19) and (20). Since a traveling wave solution u(ξ) keeps the shape and speed unchanged when parallel shifting on the ξ-axis,we let ξ0 = 0. From Fig. 4(b),we know that the best selection of the connective point is the maximum point of u(ξ),which means u′(ξ) = 0. Therefore,we take ξ = 0 as the connective point,and choose
as the connective conditions. Then,we haveSince Eq. (20) tends to 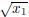 as ξ → −∞,C =
as ξ → −∞,C = 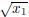 . Then,we have
. Then,we have
From the above analysis,we can derive the following theorems.
Theorem 10 If a1 < 0 and |γ | <  ,Eq. (1) has a damped oscillatory solution corresponding to the focus-saddle orbit L(P1+,P0) in Fig. 4(b),whose approximate expression is
,Eq. (1) has a damped oscillatory solution corresponding to the focus-saddle orbit L(P1+,P0) in Fig. 4(b),whose approximate expression is
Meanwhile,Eq. (1) has a damped oscillatory solution corresponding to the focus-saddle orbit L(P1-,P0) in Fig. 4(b),whose approximate expression is
where Ψ1(ξ) and B are given by Eqs. (11) and (24),A1 = −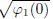 +
+ 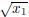 ,and A2 =
,and A2 = 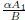 .
.
Remark 2 The value of A1 cos(Bξ) − A2 sin(Bξ) is independent of the value of B. That is to say,whether B > 0 or B < 0,its value never changes.
Theorem 11 If a1 > 0,a3 < 0,and |γ | <  ,Eq. (1) has a damped oscillatory solution corresponding to the focus-saddle orbits L(P1+,P2+) in Fig. 6(b) or Fig. 6(d),whose approximate expression is
,Eq. (1) has a damped oscillatory solution corresponding to the focus-saddle orbits L(P1+,P2+) in Fig. 6(b) or Fig. 6(d),whose approximate expression is
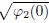 −
− 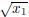 ,and A2 =
,and A2 = 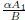 .
.
Meanwhile,Eq. (1) has a damped oscillatory solution corresponding to the focus-saddle orbits L(P1-,P2-) in Fig. 6(b) or Fig. 6(d),whose approximate expression is
where Ψ2(ξ) and B are given by Eqs. (13) and (24),A1 = −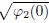 +
+ 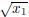 ,and A2 =
,and A2 = 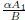 .
.
Similarly,we can derive the approximate damped oscillatory solutions,corresponding to the heteroclinic orbits L(P0,P3±) in Fig. 5(b) and L(P0,P2±) in Fig. 6(c) or Fig. 6(d),which break from the heteroclinic orbits L(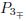 ,P3±) in Fig. 2 and L(
,P3±) in Fig. 2 and L(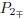 ,P2±) in Fig. 3,respectively,under the effect of dissipation term ut. The only difference is the selection of the connective point. If we still select ξ = 0 as the connective point in this case,oscillatory curve will distort seriously. Thus,we let the connective point ξ′ in the hollow neighborhood at the left side of the inflection point ξ = 0,whose radius is very small. The connective conditions will not change. Then,we can imitate the reduction of Theorem 10 to obtain the following theorem.
,P2±) in Fig. 3,respectively,under the effect of dissipation term ut. The only difference is the selection of the connective point. If we still select ξ = 0 as the connective point in this case,oscillatory curve will distort seriously. Thus,we let the connective point ξ′ in the hollow neighborhood at the left side of the inflection point ξ = 0,whose radius is very small. The connective conditions will not change. Then,we can imitate the reduction of Theorem 10 to obtain the following theorem.
Theorem 12 If a1 > 0,a3 < 0,and |γ | <  ,Eq. (1) has two damped oscillatory solutions corresponding to the focus-saddle orbits L(P0±,P3±) in Fig. 5(b) and L(P0,P2±) in Fig. 6(c) or Fig. 6(d). Their approximate expressions are
,Eq. (1) has two damped oscillatory solutions corresponding to the focus-saddle orbits L(P0±,P3±) in Fig. 5(b) and L(P0,P2±) in Fig. 6(c) or Fig. 6(d). Their approximate expressions are
In this section,we investigate error estimates of the approximate damped oscillatory so- lutions given in the previous sections. To this end,we need to find the relation between the exact and approximate damped oscillatory solutions since it is too hard to find out the exact expressions of damped oscillatory solutions. We still take the approximate damped oscillatory solution (25) corresponding to the focus-saddle orbit L(P0,P1+) in Fig. 4(b) for example. Then,other cases can be discussed similarly.
Substitute V (ξ) =  and ξ = −η (η > 0) into Eq. (7). Consequently,the problem of finding the exact damped oscillatory solution for Eq. (7),which satisfies u(0) =
and ξ = −η (η > 0) into Eq. (7). Consequently,the problem of finding the exact damped oscillatory solution for Eq. (7),which satisfies u(0) = 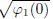 and u′(0) = 0,is converted into solving the following initial value problem:
and u′(0) = 0,is converted into solving the following initial value problem:
By the principle of homogenization,we can solve the initial value problem (30) and obtain the implicit expression of damped oscillatory solution
whereSubstitute η = −ξ and V (ξ) =  into Eq. (31),and make the transformation t = −τ. Then,we have
into Eq. (31),and make the transformation t = −τ. Then,we have
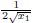 ,c1 =
,c1 = 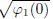 −
− 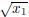 ,and c2 =
,and c2 = 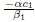 . Obviously,β1,c1,and c2 are equal to B,A1,and −A2 in Theorem 10,respectively.
. Obviously,β1,c1,and c2 are equal to B,A1,and −A2 in Theorem 10,respectively. Since damped oscillatory solution u(ξ) is bounded,there exists M > 0 satisfying |u(ξ)| < M. Moreover,from Eq. (32),we have
where By using the Gronwall inequality,the above formula becomes whereEquation (34) is the amplitude estimate of damped oscillatory solution for Eq. (1). From Fq. (34),it is easy to see that u(ξ) tends to 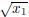 rapidly as ξ → −∞.
rapidly as ξ → −∞.
From Eqs. (32)-(34),we have
Equation (35) shows that the error estimate between the approximate solution (26) and its exact damped oscillatory solution is less than ε(ξ) =  . Due to ε1(ξ) = O
. Due to ε1(ξ) = O ,ξ → −∞,Eq. (25) is meaningful to be an approximate solution of Eq. (1) when the conditions in Theorem 10 hold.
,ξ → −∞,Eq. (25) is meaningful to be an approximate solution of Eq. (1) when the conditions in Theorem 10 hold.
By using the similar method,we can get error estimates between other approximate damped oscillatory solutions obtained above and their exact solutions. Their errors are all infinitesimal decreasing in the exponential form.
6 ConclusionsIn this paper,we analyze the shapes of the bounded traveling wave solutions for the nonlin- ear wave equation with a quintic term,and obtain the expressions according to their shapes,including exact bell and kink profile solitary solutions and approximate damped oscillatory wave solutions. Two critical values which can characterize the scale of this effect are given,where γ1 =  and γ2 =
and γ2 =  . From these two critical values,we can clearly see the dissipation influences on the shape evolution of bounded traveling wave solutions: the bounded traveling wave solutions of Eq. (1) appear as kink profile solitary waves if dissipation is large,i.e.,the dissipation coefficient γ is larger than a certain critical value; while they ap- pear as damped oscillatory waves if dissipation is small,i.e.,the dissipation coefficient γ is less than a certain critical value. We hope that the above point will help people control the system determined by Eq. (1). The approximate damped oscillatory wave solution has been proved to be reasonable. We still gave its error estimate through establishing the integral equation which reflects the relation between the exact and approximate damped oscillatory solutions by the idea of homogenization principle. The error is infinitesimal decreasing in exponential form,which also shows the advantage of this paper.
. From these two critical values,we can clearly see the dissipation influences on the shape evolution of bounded traveling wave solutions: the bounded traveling wave solutions of Eq. (1) appear as kink profile solitary waves if dissipation is large,i.e.,the dissipation coefficient γ is larger than a certain critical value; while they ap- pear as damped oscillatory waves if dissipation is small,i.e.,the dissipation coefficient γ is less than a certain critical value. We hope that the above point will help people control the system determined by Eq. (1). The approximate damped oscillatory wave solution has been proved to be reasonable. We still gave its error estimate through establishing the integral equation which reflects the relation between the exact and approximate damped oscillatory solutions by the idea of homogenization principle. The error is infinitesimal decreasing in exponential form,which also shows the advantage of this paper.
| [1] | Dodd, R. K. Solutions and Nonlinear Wave Equation, Academic Press, London (1991) |
| [2] | Wazwaz, A. M. Compactons, solitons and periodic solutions for some forms of nonlinear Klein- Gordon equations. Chaos, Solitons & Fractals, 28(4), 1005–1013 (2006) |
| [3] | Sirendaoreji. Exact travelling wave solutions for four forms of nonlinear Klein-Gordon equations. Phys. Lett. A, 363(5-6), 440–447 (2007) |
| [4] | Jang, B. New exact travelling wave solutions of nonlinear Klein-Gordon equations. Chaos, Solitons & Fractals, 41(2), 646–654 (2009) |
| [5] | Ye, C. and Zhang, W. G. New explicit solutions for the Klein-Gordon equation with cubic non- linearity. Appl. Math. Comp., 217(2), 716–724 (2010) |
| [6] | Farlow, S. J. Partial Differential Equations for Scientists and Engineers, Wiley InterScience, New York (1982) |
| [7] | Fan, E. G. and Zhang, H. Q. The solitary wave solution for a class of nonlinear wave equations (in Chinese). Acta Phys. Sin., 46(7), 1254–1258 (1997) |
| [8] | Shang, Y. D. Explicit and exact solutions for a class of nonlinear wave equations (in Chinese). Acta Math. Appl. Sin., 23(1), 21–30 (2000) |
| [9] | Zhang,W. G., Chang, Q. S., and Fan, E. G. Methods of judging shape of solitary wave and solution formulae for some evolution equations with nonlinear terms of high order. J. Math. Appl., 287(1), 1–18 (2003) |
| [10] | Li, X., Zhang, W. G., and Zhao, Y. Shape analysis and solution to a class of nonlinear wave equation with cubic term. Adv. Appl. Math. Mech., 4(5), 559–574 (2012) |
| [11] | Zhang, W. G. and Ma, W. X. Explicit solitary-wave solutions to generalized Pochhammer-Chree equations. Appl. Math. Mech., 20(6), 666–674 (1999) |
| [12] | Ye, C. New exact solutions for the nonlinear wave equation with fifth-order nonlinear term. Appl. Math. Comput., 218(5), 2155–2166 (2011) |
| [13] | Taogetusang and Sirendaoerji. New exact solitary wave solutions for nonlinear wave equation with fifth-order strong nonlinear term constructed by hyperbolic function type of auxiliary (in Chinese). Acta Phys. Sin., 55(1), 13–18 (2006) |
| [14] | Naranmandula, Wunenboyn, and Wang, K. X. New solitary wave solutions for nonlinear wave equation with fifth-order strong nonlinear term (in Chinese). Acta Phys. Sin., 53(1), 11–14 (2004) |
| [15] | Li, J. and Zhang, L. Bifurcations of traveling wave solutions in generalized Pochhammer-Chree equation. Chaos, Solitons & Fractals, 14, 581–593 (2002) |
| [16] | Li, J. and Dai, H. H. On the Study of Singular Nonlinear Traveling Wave Equations. Dynamical System Approach, Science Press, Beijing (2007) |
| [17] | Zhang, L., Chen, L., and Huo, X. The effects of horizontal singular straight line in a generalized nonlinear Klein-Gordon model equation. Nonlinear Dynamics, 72(4), 789–801 (2013) |
| [18] | Zhang, Z. F., Ding, T. R., Huang, W. Z., and Dong, Z. X. Qualitative Theory of Differential Equations, Translations of Mathematical Monographs, American Mathematical Society, Provi- dence (1992) |
| [19] | Nemytskii, V. V. and Stepanov, V. V. Qualitative Theory of Differential Equations, Dover Publi- cations, New York (1989) |
 2014, Vol. 35
2014, Vol. 35















































