The Chinese Meteorological Society
Article Information
- K.GAYATHRI,K.SHAILENDHRA 2014.
- Pulsatile blood flow in large arteries: comparative study of Burton’s and McDonald’s models
- Appl. Math. Mech. -Engl. Ed., 35 (5) : 575–590
- http: //dx. doi. org/10.1007/s10483-014-1814-7
Article History
- Received 2013-09-22;
- in final form 2013-11-04
Nomenclature
x, horizontal coordinate axis (m);
y, vertical coordinate axis (m);
u, x-component of velocity (m · s −1);
v, y-component of velocity (m · s −1);
t, time (s);
h, half width of channel (m);
ρ, density of blood (kg · m −3);
μ, viscosity of blood (kg · m −1 · s −1);
p, pressure (Pa);
∇p, pressure gradient (Pa · m −1);
a0, steady part of pressure gradient (Pa · m −1);
an, unsteady part of pressure gradient (Pa · m −1);
αn, phase angle;
k, permeability of wall (m2);
α, Beavers and Joseph (BJ) slip coefficient;
Q, steady part of Darcy velocity (m · s −1);
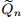 , unsteady part of Darcy velocity (m · s −1);
, unsteady part of Darcy velocity (m · s −1);
uB, slip-velocity at interface (m · s −1);
f, heart frequency (Hz)
ω, angular frequency 2πf (rad · s −1);
α, Womersely number
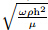 .
1 Introduction
.
1 Introduction
The pulsatile nature of blood flow,especially the pressure pulse,is known to be a leading hemodynamicrisk factor for coronary heart disease and heart failure which leads to the malfunction of car diovascular system. Also,both high low-density and low high-density lipoprotein levels are associated with an elevated plasma viscosity,which in turn is associated with increased incidents of these diseases[1]. Cigarette smoking,lack of exercise,obesity,hypertension,concentration of lipids in the blood,etc. are some of the risk factors believed to cause cardiovascular diseases[2]. Texon[3] and Stehbens[4] ,strong proponents of hemodynamic or mechanical causes of atherosclerosis,challenged the cholesterol-heart disease hypothesis by establishing that studies on such a hypothesis were statistically flawed and inconclusive. Indeed,Texon[3] concluded that the hemodynamic factors were the main causative factors in localization,inception,and progressive development of atherosclerosis. Further,he related the pathogenesis of atherosclerosis to a reactive biologic response of arteries to the diminished lateral pressure by flowing blood. It is known that the hemodynamic factors like pulsatile velocity of blood,wall shear stress (WSS),oscillatory shear index (OSI),resistance to flow due to change in blood viscosity, and blood pressure play an important role in the normal adaptive response of blood vessels to chronic changes in physiologic demands and in maladaptive responses leading to cardiovascular disease[5, 6] . The vascular endothelium is known to have different behavioral responses depending on altered flow patterns both at the molecular and cellular levels. These reactions are believed to promote atherosclerosis in synergy with other well-defined systemic risk factors cited above[5].
Fry[7] emphasized the need for fluid-mechanical study of cardiovascular disease,and he showed that the endothelial wall deterioration and growth were closely related to the WSS acting on the cells. Subsequently,such a fluid mechanical study of the blood flow in a vessel with atherosclerosis was initiated by Lee and Fung[8] .
It is well-known that blood flow would be modeled as pulsatile,three-dimensional flow of a non-Newtonian fluid in a vessel of varying cross-section. The wall is elastic in nature,and healthy functioning of the arterial wall is based on the wall compliance and resistance to flow based upon the cardiac output. However,to study the non-linear problem of the coupling between the pulsatile blood flow and the motion of the vessel wall is beyond today’s computational capabilities[9] . Further,the arterial walls are porous in nature which will introduce additional mathematical complexities. Incidentally,Ku[10] pointed out that the pulsatile nature of the blood flow was more important,and the other factors like the vessel wall elasticity, non-Newtonian viscosity,slurry particles in the fluid,body forces,and temperature were secondary in importance and could be neglected. Further,he also indicated that in most of the arterial flows,the above mentioned secondary effects could be justifiably neglected even though they were physiologically relevant. An excellent and comprehensive review on blood flow in arteries,under various physical situations,was rendered by Nichols and O’Rourke[1].
Blood flow through the vessel must be considered as pulsatile due to the rhythmic pumping action of the heart[1]. It must be noted here that in most of the earlier investigations[11, 12, 13] ,the pulsatile nature of blood flow was modeled as
where A0 is the constant amplitude of pressure gradient,A1 is the amplitude of pulsatile component giving rise to the systolic and diastolic pressure,ω = 2πf is the pulse frequency, and f is the heart frequency. This model of the pressure gradient was attributed to Burton[14] and the references cited above.
Chaturani and Bharatiya[15] in their work criticized that the pressure gradient used in the literature was either too ideal or incorrect. In their work,they considered ten harmonics in Fourier series to approximate Milnor’s experimental pressure gradient of human pulmonary artery.
Earlier in 1927,Frank seems to be the first person to theoretically employed Fourier series to describe the pulsatile nature of the pressure gradient. However,it is only after the pioneering works of Womersely and McDonald during 1955 ,the concept of approximating the pressure gradient by Fourier series with an adequate number of harmonics obtain a momentum in the field of cardiovascular physiology[1].
Indeed,to be more realistic,in 1960 McDonald insisted that adequate numbers of harmonics were to be considered in the Fourier series approximation of the pressure gradient to describe the complete pulsatile nature of the waveform as[1]
where “m” refers to the number of harmonics. Several studies[15, 16, 17] have been carried out following the lines of McDonald. For convenience,in the present study,(1) and (2) will be referred to as Burton’s model and McDonald’s model,respectively. In general,the pressure gradient ∂p/∂x in any artery will be a function of not only “t” but also “x”. Some models of this type have been developed as
where
where q(x) is not known explicitly and is computed by assuming the steady flow rate as a known quantity as in Ref. [18]. However,McDonald’s model (see (2)) does not capture the variation of pressure gradient along the axial direction “x”. Hence,all results reported here are applicable only locally where the pressure gradient is measured.
Further,McDonald and Womersley categorically established that the arterial system could be considered as a linear system and that the non-linear terms were indeed sufficiently small that they could be neglected to a first-order approximation. As a consequence,the arterial system could be viewed as being in a steady state of oscillation and so could validly be analyzed in the frequency domain[1] . Later,it was also confirmed by many experiments that the non-linear effects could be neglected and such details could be found in Ref. [1]. Thus,the question of considering the arterial system as a linear system is no longer a subject of contention,and there is far less controversy on this issue than there was in the past[1].
In the literature of blood flow,considerable efforts have been devoted to investigate the role of hemodynamic factors in locations prone to atherosclerosis. However,it is now recognized that it is necessary to carry out such investigations in regions relatively free of atherosclerosis, also it is recognized that they might provide further quantitative and qualitative insights in this regard[19]. Indeed,it is recognized that hemodynamic factors are equally important in the pulmonary vasculature as they are in the systemic vasculature[20],despite the fact that the pulmonary artery is spared from neointimal hyperplasia or atherosclerosis,except under the pulmonary hypertension,owing to the fact that the substantially lower blood pressure in it is atheroprotective.
Thus,motivated by the realistic approach of McDonald’s model and the earlier work of Chaturani and Bharatiya[15],an attempt is made here to investigate the blood flow in large arteries,both in systemic and pulmonary circulatory systems (femoral,brachial,and pulmonary artery). The flow is considered to be pulsatile,and the pressure gradient in each of the above arteries is modeled as realistically as possible by approximating it by a Fourier series expansion with an adequate number of harmonics (McDonald’s model). The wall is assumed to be rigid and permeable,and the flow inside the porous wall is described by the Darcy law. The wellknown Beavers and Joseph (BJ) slip condition is employed at the interface[21]. An analytic solution for the velocity of blood in the lumen is obtained,and elaborate investigations on WSS and OSI are carried out. The above analyses are also carried out using the commonly employed Burton’s model. The results obtained using the above two models are c mpared with available data in the literature. To the best of our knowledge,this is the first explicit and elaborate comparison of the two models ,and it is believed that this investigation will improve our understanding of the pulsatile nature of blood flow. Finally,by reviewing the limitations of the present investigation,the possibilities of improving it are explored. 2 Mathematical formulation and solution
The assumptions ,for the sake of mathematicals implicity,along with the justifications ,if any,are presented below :
(i) Blood is assumed to be Newtonian. It is known that blood can be treated to be Newtonian if the vessel wall radius is greater than 0.00025 m and the shear rate is greater than 100s−1[1] . In the present study,we consider the femoral,brachial,and pulmonary artery whose radii are greater than 0.000 25 m,which justify the neglect of non-Newtonian effect. Further, Taylor[22] concluded that for the large arteries only relatively small errors were introduced by the assumption of a constant viscosity coefficient.
(ii) Cross-section of the artery is assumed to be uniform,and the flow is approximated as a flow through a uniform channel,which is usually done for axisymmetric flows. In reality,this is not true,and this assumption is made only for the sake of mathematical simplicity so that it is enough to deal with hyperbolic functions instead of the Bessel functions.
(iii) The length of the artery is assumed to be sufficiently larger than its radius,so that the flow can be regarded to be one-dimensional.
(iv) Arterial wall elasticity is neglected as suggested by Ku[10] .
(v) The wall is approximated as a single porous layer though it is known to be made up of several layers. Having considered the wall as mono-layer,the Darcy law is employed to describe the flow inside the wall,and the BJ slip condition is used at the lumen-wall interface[21].
(vi) Having neglected the transmural and osmotic pressure,it is assumed that the flow inside the wall is also driven by the same pressure gradient that drives blood in the lumen.
Consider the laminar pulsatile flow of blood in a uniform channel of width 2h bounded by rigid infinite porous walls at y = ±h. The continuity equation and the Navier-Stokes equation, in a Cartesian coordinate system (x,y),reduce to
where ρ,μ,and p are the density,the coefficient of viscosity,and the pressure of the blood, respectively,The governing u is the velocity components in the axial direction,and t is the time.
The governing equation describing the flow inside the wall is given by the Darcy law as follows:
The flow at the interface between the lumen and the wall is matched with the BJ slip condition[21] given by
where α,k,uB,and Q,respectively,refer to the BJ slip coefficient,permeability of the the porous wall,slip-velocity,and Darcy velocity. Following McDonald’s model (see (2)),the pressure gradient in (4) is approximated as
where
and “m” denotes the number of harmonics as mentioned earlier. The pressure gradient waveforms of human femoral,brachial,and pulmonary arteries are taken from Sharp et al.[23] , Anssari-Benam and Korakianitis[24],and Milnor[25],respectively. The digitized data from these waveforms are then used to estimate the Fourier coefficients in (9) to approximate the original waveforms. We take m=50,60,and 50 for the above arteries,respectively. The details of the Fourier coefficients involved in the above approximations are presented in Appendix A1. For the sake of comparison,the original pressure gradient waveforms and their Fourier series approximations are presented in Fig. 1.
 |
| Fig. 1. Pressure gradient waveforms of human arteries. |
The root mean square error in the above approximation is estimated numerically using
 ,where F(t) is the Fourier series approximation corresponding
to the original pressure gradient f(t) and is given in Table 1. However,by considering 50
harmonics,we are able to match the waveform with an error E=0.76 Pa · cm −1.
,where F(t) is the Fourier series approximation corresponding
to the original pressure gradient f(t) and is given in Table 1. However,by considering 50
harmonics,we are able to match the waveform with an error E=0.76 Pa · cm −1.
Incidentally,Chaturani and Bharathiya[15] approximated Milnor’s experimental pressure gradient of human pulmonary artery by taking ten harmonics. However,we find that their curve is shifted to the right by 0.41 seconds and is not matching with the original waveform.
Womersely and McDonald established that the arterial system could be considered as a linear system and that any harmonic component of pressure wave could be related to the same harmonic of another pressure or flow wave recorded at the same time and to no other harmonic[1]. Accordingly,the velocity u(y,t) in the lumen and the Darcy velocity Q(t) in the arterial wall can be modeled as follows:
where the symbol “ −” denotes the steady part and the symbol “ ~” denotes the unsteady part.
It must be noted here that the Darcy velocity Q(t) and the slip velocity uB(t) are expanded
as Fourier series given by (11) and (12) in order to breakdown each of the BJ slip conditions
(see (7) and (8)) into (m + 1) boundary conditions,one pertaining to the steady part u(y) and
the remaining “m” conditions pertaining to the “m” harmonics  . This approach is quite
justified since the arterial system is assumed to be linear.
. This approach is quite
justified since the arterial system is assumed to be linear.
The characteristic length (h),time (1/ω),and velocity (hω) are used to non-dimensionalize the above equations. Henceforth,all quantities are in the non-dimensional form. Thus,for the sake of notational convenience,we retain the symbols as follows:
where
Here,1/σ is called the Darcy number,and α is called the Womersely number. Solving the above equations,we get
On the other hand,the velocity of blood in the lumen using Burton’s model is given by
where u(y) is given in (19),
2.1 WSS and OSIThe WSS on the upper wall is given by
As blood flows across the endothelium,a shear stress is generated to retard the flow. WSS is known to be very significant in controlling the atheroprotective,normal physiology as well as the pathobiology and dysfunction of vessel wall through complex molecular mechanisms that are believed to promote atherogensis[5]. The localizations of atherosclerotic plaques in regions of complex flow are attributed to low mean WSS (< 0.4 Pa) along with the flow recirculation and high particle residence time. In the regions of low WSS,enhancement of cholesterol accumulation is noticed. Further,elevated WSS is found to prevent the formation of atherosclerosis[26].
It is well-known that the vascular wall is continuously fine-tuning its activities in response to vascular shear stress. The endothelial wall acts as a sensor of WSS and depends on the magnitude of WSS,and it triggers various chemical responses by a process called mechanotransduction and such responses may be atheroprotective or may cause atherosclerosis or aneurysm[6] . Indeed,endothelial cells sense WSS by several possible mechanisms and in turn act as a shear stress transducer including those mediated and not mediated by gene expression. Once the WSS is mechanosensed by the endothelial cells initially,cells surfaces and cell membranes may be deformed,ions may be translocated,local biochemical responses may be activated,downstream intracellular signaling pathways may be expressed,all to modulate shear-induced endothelial function as well as important shear-induced alterations in endothelial cell morphology[5]. It is not possible and appropriate here to elaborate further on the role of WSS in the regulation of the blood vessel responses by the mechanotransduction mechanisms that lead to biophysical, biochemical and gene regulatory responses of endothelial cells,and for further details one may refer to the excellent comprehensive review article by Davies[6] .
To quantify the temporal oscillations in shear stress,OSI is defined as by He and Ku[27]
where T is the pulse period in seconds,and
This non-dimensional index quantifies the pulsatility and the time in the particular wall region in the cycle experiences cross or reverse flow. Its value ranges from 0 to 0.5,and it represents the fraction of the cardiac cycle over which the instantaneous shear force vector forms an angle greater than 90◦ to the time-averaged direction of the same force. Here,I1 represents the absolute value of the total WSS (the sum of all positive and negative WSS),and I2 represents the sum of all absolute values of the WSS over a cardiac cycle. Taylor et al.[28] and Buchanan et al.[29] observed that the regions of low mean WSS and high OSI both coincide with a high probability of occurrence of early atherosclerotic lesions,and Olgac et al.[30] reported that a region of low mean WSS and high OSI coincided with the location of a plaque.
Mean WSS and OSI for the three considered arteries are calculated numerically. 2.2 Results
In an earlier work,Shivakumar et al.[31] idealized blood flow in arteries as a laminar steady flow of incompressible,viscous,and Newtonian fluid between homogeneous porous channel of varying gap with infinite thickness by employing the BJ slip boundary condition at the interface, by eliminating the pressure gradient term and by assuming the flux to be a known quantity. The purpose of the present work is to extend exclusively the uniform channel flow considered in the above problem by considering a pulsatile flow instead of steady flow by assuming that the pressure gradient is known.
In our computation,we fix ρ = 1050 kg·m−3,μ = 0.004 kg·m−1·s−1,α = 0.1 (see Ref. [32]),and f = 1.2 Hz,which are often used in blood flow,for the density,the coefficient of viscosity,the BJ slip coefficient,and the heart frequency,respectively. The radii of femoral,brachial,and pulmonary artery are fixed respectively as 0.0033 m,0.00165 m, and 0.0135 m[24, 25, 33] . Whale et al.[34] measured the permeability of ostensibly healthy human aortic wall to be k = (2.9 ± 0.3) × 10−18 m2,and we assume that this value is also suitable for the large sized human arteries that we have considered here.
Hemodynamic factors like velocity of blood in lumen,WSS and OSI for all the three arteries are calculated using both Burton’s and McDonald’s models. Also the mean,peak,and minimum values of the center-line velocity and WSS for the three arteries are found. All results are presented in Figs. 2−7 and in Tables 2−5.
 |
| Fig. 2. Centre-line velocity of femoral artery. |
 |
| Fig. 3. Centre-line velocity of brachial artery. |
 |
| Fig. 4. Centre-line velocity of pulmonary artery. |
 |
| Fig. 5. WSS of femoral artery. |
 |
| Fig. 6. WSS of brachial artery |
 |
| Fig. 7. WSS of pulmonary artery. |
From Figs. 2 −4,it is clear that the velocity waveforms obtained using the two models are radically different.
From Tables 2 and 3,it is observed that,in all the three arteries,the peak and the minimum velocities are different in the above two models. However,the mean velocity is found to be the same in both models. It can be noted that the steady part u0(y) of the velocity (and hence the center-line velocity u0(0)) is the same for both the models since it corresponds to the steady part A0 of the pressure gradient,which is the same in the both models. Thus,if the mean velocity is sufficient in a given context,then one may employ any one of these models.
The orders of magnitude of the mean center-line velocities obtained here for all the three arteries are in good agreement with the data available in the literature[33, 35] . However,in the pulmonary artery,the mean center-line velocity is found to be 26.94 cm ·s−1,which is significantly larger than the value 19 cm ·s−1 reported in Ref. [33]. This deviation may possibly be attributed to the fact that the cross-section of the pulmonary artery is actually elliptical and not circular,and hence our assumption of axisymmetric flow may not be appropriate for this artery. Further,though the wall structures are similar,the parameter values are very different for the systemic and pulmonary arteries[36]. Thus,we are not very sure whether the permeability value assumed here is applicable for pulmonary artery or not.
From Figs. 5 −7,it is observed that in McDonald’s model,the WSS oscillates more rapidly with respect to time in comparison to Burton’s model. In the brachial artery,in both models,the WSS is completely negative throughout the cycle. This indicates the fact that,physically, there is no cyclic variation in the direction of WSS. Due to this,the two integrals I1 and I2 in the definition of OSI have the same value. Therefore,the OSI is found to be zero in both models. Biologically,this means that there is no damage to the endothelial cells. Incidentally,the magnitude of mean WSS is 2.184 Pa. It is in the normal range 1 Pa −7 Pa,which is considered to be atheroprotective[37].
In the case of femoral artery,the WSS is completely negative in Burton’s model whereas there is a small interval of time,in which the WSS is positive in McDonald’s model. As a consequence,OSI estimated using Burton’s model is zero whereas it is 0.045 4 in McDonald’s model. According to Burton’s model,biologically this means that the WSS is unidirectional and hence throughout the cardiac cycle the alignment of the endothelial cells remains in this unique direction of WSS,and it is not disturbed at all. However,according to McDonald’s model,the direction of WSS changes slightly and hence in a cardiac cycle the direction of alignment of the endothelial cells will be disturbed accordingly. The magnitude of mean WSS is found to be 0.254 5 Pa which is considered to be a low shear region indicating the possibility of formation of atherosclerosis[37].
In Burton’s model of the pulmonary artery,the WSS almost remains negative throughout the cycle,except in a very small interval of time. However,it rapidly changes its sign in McDonlad’s model. This is the reason why the OSI is found to be 0.032 6 in Burton’s model,whereas it is 0.374 4 in McDonald’s model. Thus,according to McDonald’s model,the direction of alignment of endothelial cells will be greatly disturbed in a cardiac cycle which is not predicted by Buton’s model. Further,since the OSI is on the higher side,in McDonald’s model,it indicates that the time-averaged fluctuations in the shear stress I1 created by forward-reverse flow cycles and disrupted flows are relatively low compared with I2,and this may correspond to regions of flow separation,recirculation and reattachment that are associated with temporal and spatial shear gradients[5]. Further,a high value of OSI is postulated to disrupt the atheroprotective molecular pathways reducing the production of nitric oxide (NO) and thus changing the biology of the vessel which in turn induces plaque formation and subsequent disruption in blood flow that leads to atheroma progression and potentially imparts vulnerability onto atherosclerotic lesions[5] .
Finally,from Tables 4 and 5,it is observed that the mean values of the WSS in both
models are the same for all the three arteries,and they are equal to  evaluated at the
upper wall of the respective arteries. Incidentally,Malek et al.[37] reported that the magnitude of the mean WSS in normal artery ranges from 1Pa −7Pa whereas in the atherosclerosis-prone
arterial region,it varies between ±0.4Pa,and in high shear thrombosis region,it ranges from
7Pa −10Pa or more. Since the magnitude of the mean WSS of femoral and pulmonary artery is
less than 0.4Pa,theoretically there is a possibility for the formation of atherosclerosis. However,
the OSI for the femoral artery is too low,and for the pulmonary artery it is sufficiently high.
Therefore,it appears as though the pulmonary artery is more prone to atherosclerosis than
the femoral artery. However,it is well-known that the pulmonary artery is less susceptible to
atherosclerosis except under the pulmonary hypertension[20]. Perhaps,the subject from whom
the pressure gradient was recorded might have had pulmonary hypertension. We believe that
further investigation by considering the cross-section of the pulmonary artery to be elliptic
would enable us to get a clear picture in this regard. Further,the mean WSS of the brachial
artery is high,and the OSI is zero,which indicates that the subject from whom the pressure
gradient was recorded is not susceptible for the formation of atherosclerosis in this artery.
evaluated at the
upper wall of the respective arteries. Incidentally,Malek et al.[37] reported that the magnitude of the mean WSS in normal artery ranges from 1Pa −7Pa whereas in the atherosclerosis-prone
arterial region,it varies between ±0.4Pa,and in high shear thrombosis region,it ranges from
7Pa −10Pa or more. Since the magnitude of the mean WSS of femoral and pulmonary artery is
less than 0.4Pa,theoretically there is a possibility for the formation of atherosclerosis. However,
the OSI for the femoral artery is too low,and for the pulmonary artery it is sufficiently high.
Therefore,it appears as though the pulmonary artery is more prone to atherosclerosis than
the femoral artery. However,it is well-known that the pulmonary artery is less susceptible to
atherosclerosis except under the pulmonary hypertension[20]. Perhaps,the subject from whom
the pressure gradient was recorded might have had pulmonary hypertension. We believe that
further investigation by considering the cross-section of the pulmonary artery to be elliptic
would enable us to get a clear picture in this regard. Further,the mean WSS of the brachial
artery is high,and the OSI is zero,which indicates that the subject from whom the pressure
gradient was recorded is not susceptible for the formation of atherosclerosis in this artery.
To summarize,in McDonald’s model,the mean WSS is low,and OSI is high in the pulmonary
artery,the mean WSS is low and OSI is also low in the femoral artery,and the mean WSS is in
a normal range and OSI is zero in the brachial artery. Thus,it may be inferred that a low mean
WSS is not the reason for a high OSI and that they do not co-locate. Further,it is inferred
that the OSI depicts only the fluctuation in the direction of WSS over a cardiac cycle,and its
value does not depend on the magnitude of WSS,as already reported in Ref. [38]. Hence,it
is not very clear whether the reason for atherosclerosis is the low mean WSS or high OSI or
both. In this context,it is important to note here that Peiffer et al.[39] in their very recent
review article concluded that the evidence for the low/oscillatory shear theory for the formation
of atherosclerosis is less robust than commonly assumed. From the above observations,it is
inferred that McDonald’s model is better than Burton’s model in capturing the real pulsatile
nature of the blood flow,as is physically expected. It must be noted here that the pressure
gradient waveforms of the three considered arteries are taken from different sources[23, 24, 25],which
are measured from different subjects with unknown cardiovascular history. Further,since the
radius of the femoral artery is not mentioned in the original source,its value is taken from
a different source[33]. We believe that the accuracy and reliability of the investigation can
be improved if all the physiological parameters like viscosity,density,radius,permeability are
subject specific and artery specific. Whereas in the present investigation the cross-section of
the arteries is assumed to be uniform,and in reality the vessel cross-section varies in the axial
direction. Also,the BJ slip condition employed at the interface is valid under the assumption
that the thickness of the wall is larger compared with the radius of the lumen. In reality,the wall
thickness is very very small compared with the lumen radius in medium and large sized blood
vessels. Further,it is found that during computation,the order of magnitude of Darcy velocity
is 10−12 m · s−1 and the order of magnitude of slip-velocity is 10−4 m · s−1. Thus,it is inferred
that the Darcy velocity can be neglected in the BJ slip conditions and accordingly,it appears as
though one may employ any one of the following slip boundary conditions: Saffman condition,
 or Navier condition,
or Navier condition, ,where Ap is a coefficient close to the
mean free path of the molecules of the blood. If this alternative approach is employed,then
there will not be any necessity to model the flow inside the arterial wall,and the limitation
imposed by the assumption number (vi) in Section 2 can be avoided. In such a case,it is
envisaged that there will not be any significant change in our results,both qualitatively and
quantitatively.
3 Conclusions
,where Ap is a coefficient close to the
mean free path of the molecules of the blood. If this alternative approach is employed,then
there will not be any necessity to model the flow inside the arterial wall,and the limitation
imposed by the assumption number (vi) in Section 2 can be avoided. In such a case,it is
envisaged that there will not be any significant change in our results,both qualitatively and
quantitatively.
3 Conclusions
A comparative study of pulsatile blood flow in large arteries using Burton’s and McDonald’s models for pressure gradient with the BJ slip condition at the lumen-wall interface has been carried out in three different arteries,which includes the femoral and the brachial from the sys- temic side and the pulmonary artery. To the best of our knowledge,this is the first explicit and extensive investigation comparing the two models mentioned above. Subject to the limitations of our investigation mentioned in the last paragraph of the previous section,we summarize our observations as follows.
(i) As it is physically expected,compared with Burton’s model,McDonald’s model captures the pulsatile nature of blood flow,in particular the value of OSI,in a better way.
(ii) The orders of magnitude of mean center-line velocity of the femoral and brachial arteries are in good agreement with the data available in the literature. However,in the pulmonary artery it is significantly larger than the data reported in the literature. Further,comparing our results on WSS with the earlier investigations,we find that the WSS of brachial artery corresponds to a normal artery and that the femoral and the pulmonary artery are susceptible to atherosclerosis. The OSI value suggests that the pulmonary artery is more susceptible than the femoral artery,though it is well-known that the pulmonary artery is relatively free from the atherosclerosis. Detailed discussion in this regard is presented in the previous section.
(iii) Further,our investigation is in support of the hypothesis that not only WSS but also OSI is an important factor determining atherogensis. Our results indicate that the low mean WSS is not the reason for a high OSI and that OSI depicts only the fluctuation in the direction of WSS over a cardiac cycle and its value does not depend on the magnitude of WSS.
Acknowledgement We are grateful to the anonymous reviewers for their critical comments which enable us in improving the quality of the article substantially.
| [1] | Nich ols, W . W . an d O ’R ou rke, M. F. McDonald’s Blood Flow in Arteries, Theoretical, Experimental and Clinical Principles, Oxford University Press,New York (2005) |
| [2] | Hall, R. J. Atherosclerosis past, present, and future. Texas Heart Institution Journal, 17(3), 148–156 (1990) |
| [3] | Texon, M. Hemodynamic Basis of Atherosclerosis, Hemisphere, Washington, D. C. (1980) |
| [4] | Stehbens, W. E. Flaws in the lipid hypothesis of atherogensis. Pathology, 20(4), 395–396 (1988) |
| [5] | Cunningham, K. S. and Gotlieb, A. I. The role of shear stress in the pathogenesis of atherosclerosis.Laboratory Investigation, 85(1), 9–23 (2005) |
| [6] | Davies, P. F. Flow-mediated endothelial mechanotransduction. Physiological Reviews, 75(3), 519–560 (1995) |
| [7] | Fry, D. L. Acute vascular endothelial changes associated with increased blood velocity gradients.Circulation Research, 22, 165–197 (1968) |
| [8] | Lee, J. S. and Fung, Y. C. Flow in locally constricted tubes at low Reynolds number. Journal ofApplied Mechanics, 37, 9–16 (1970) |
| [9] | Suncica, C., Josip, T., Giovanna, G., Andro, M., Craig, J. H., and Doreen, R. Modeling viscoelastic behavior of arterial walls and their interaction withpulsatile blood flow. Society for Industrial and Applied Mathematics, 67(1), 164–193 (2006) |
| [10] | Ku, D. N. Blood flow in arteries. The Annual Review of Fluid Mechanics, 29, 399–434 (1997) |
| [11] | Ilyani, A., Norsarahaida, A., and Tasawar, H. Magnetohydrodynamic effects on blood flow throughan irregular stenosis. International Journal for Numerical Methods in Fluids, 67(11), 1624–1636(2011) |
| [12] | Misra, J. C. and Shit, G. C. Effect of magnetic field on blood flow through an artery: a numericalmodel. Journal of Computational Technologies, 12, 3–16 (2007) |
| [13] | Ogulu, A. and Amos, E. Modeling pulsatile blood flow within a homogeneous porous bed in thepresence of a uniform magnetic field and time-dependent suction. International Communicationsin Heat and Mass Transfer, 34(8), 989–995 (2007) |
| [14] | Bu rt on , A . C. Physiology and Biophysics of the Circulation, Book Medical Publisher, Chicago(1966) |
| [15] | Chaturani, P. and Bharatiya, S. S. Magnetic fluid model for two-phase pulsatile flow of blood.Acta Mechanica, 149, 97–114 (2001) |
| [16] | Ariman, T., Turk, M. A., and Sylvester, N. D. On steady and pulsatile flow of blood. Journal ofApplied Mechanics, 41(1), 1–7 (1974) |
| [17] | Somkid, A., Benchawan, W., Wu, Y. H., and Yongwimon, L. Effect of non-Newtonian behaviour ofblood on pulsatile flows in stenotic arteries. International Journal of Biological and Life Sciences,1(1), 42–46 (2005) |
| [18] | Devajyoti, B. and Uday, S. C. Pulsatile blood flow through a catheterized artery with an axiallynonsymmetrical stenosis. Applied Mathematical Sciences, 4(58), 2865–2880 (2010) |
| [19] | Taylor, C. A. and Humphrey, J. D. Open problems in computational vascular biomechanics: hemodynamics and arterial wall mechanics. Computer Methods inApplied Mechanics and Engineering,198(45), 3514–3523 (2009) |
| [20] | Botney, M. D. Role of hemodynamics in pulmonary vascular remodeling implications for primarypulmonary hypertension. American Journal of Respiratory and Critical Care Medicine, 159(2),361–364 (1999) |
| [21] | Beavers, G. S. and Joseph, D. D. Boundary conditions at a naturally permeable wall. Journal of |
| [22] | Taylor, M. G. The influence of the anomalous viscosity of blood upon its oscillatory flow. Physicsin Medicine and Biology, 3, 273–290 (1959) |
| [23] | Sharp, M. K., Thurston, G. B., and Moore, J. E. The effect of blood viscoelasticity on pulsatileflow in stationary and axially moving tubes. Biorheology, 33(3), 185–208 (1996) |
| [24] | Anssari-Benam, A. and Korakianitis, T. An experimental model to simulate arterial pulsatileflow: in vitro pressure and pressure gradient wave study. Experimental Mechanics, 53(4), 649–660(2013) |
| [25] | Milnor, W. Hemodynamics, Williams and Wilkins, Baltimore (1989) |
| [26] | Taylor, C. A., Christopher, P., Cheng, L. A. E., Beverly, T., David, P., and Robert, J. H. In vivoquantification of blood flow and wall shear stress in the human abdominal aorta during lower limbexercise. Annals of Biomedical Engineering, 30, 402–408 (2002) |
| [27] | He, X. and Ku, D. N. Pulsatile flow in the human left coronary artery bifurcation: averageconditions. Journal of Biomechanical Engineering, 118(1), 74–82 (1996) |
| [28] | Taylor, C. A., Hughes, T. J. R., and Zarins, C. K. Finite element modeling of three-dimensionalpulsatile flow in the abdominal aorta: relevance to atherosclerosis. Annulus of Biomedical Engineering, 26(6), 975–987 (1998) |
| [29] | Buchanan, J. R., Kleinstreuer, C., Hyun, S., and Truskey, G. A. Hemodynamics simulation andidentification of susceptible sites of atherosclerotic lesion formation in a model abdominal aorta.Journal of Biomechanics, 36, 1185–1196 (2003) |
| [30] | Olgac, U., Poulikakos, D., Saur, S. C., Alkadhi, H., and Kurtcuoglu, V. Patient-specific threedimensional simulation of LDL accumulation in a human leftcoronary artery in its healthy andatherosclerotic states. American Journal of Physiology-Heart and Circulatory Physiology, 296,H1969–H1982 (2009) |
| [31] | Shivakumar, P. N., Nagaraj, S., Veerabhadraiah, R., and Rudraiah, N. Fluid movement in achannel of varying gap with permeable walls covered by porous media. International Journal ofEngineering Science, 24(4), 479–492 (1986) |
| [32] | Dulal, P., Veerabhadraiah, R., Shivakumar, P. N., and Rudraiah, N. Longitudinal dispersion oftracer particles in a channel bounded by porous media using slip condition. International Journalof Mathematics and Mathematical Science, 7(4), 755–764 (1984) |
| [33] | Ross-Ethier, C. and Craig, A. S. Introductory Biomechanics: From Cells to Organisms, CambridgeUniversity Press, Cambridge (2007) |
| [34] | Whale, M. D., Grodzinsky, A. J., and Johnson, M. The effect of aging and pressure on the specifichydraulic conductivity of the aortic wall. Biorheology, 33(1), 17–44 (1996) |
| [35] | S in oway, L . I ., H en d r ick son , C., D av id son , W . R ., Prop h et , S ., an d Z elis, R . Ch ar act erist ics offl ow- m ed iat ed b rach ial art ery vasco d ilat ion in hu m an su b ject s. Circulation Research, 64, 32–42(1989) |
| [36] | Zeng, Z. Q., Jan, K. M., and Rumschitzki, D. S. A theory for water and macromolecular transportin the pulmonary artery wall with a detailed comparison to the aorta. American Journal ofPhysiology-Heart and Circulatory Physiology, 302, H1683–H1699 (2012) |
| [37] | Malek, A. M., Alper, S., and Izumo, S. Hemodynamic shear stress and its role in atherosclerosis.The Journal of the American Medical Association, 282(21), 2035–2042 (1999) |
| [38] | Younis, H. F., Kaazempur-Mofrad, M. R., Chan, R. C., Isasi, A. G., Hinton, D. P., Chau, A. H.,Kim, L. A., and Kamm, R. D. Hemodynamics and wallmechanics in human carotid bifurcationand its consequences for atherogenesis: investigation of inter-individual variation. Biomechananicsand Modeling Mechanobiology,3, 17–32 (2004) |
| [39] | Peiffer, V., Sherwin, S. J., and Weinberg, P. D. Does low and oscillatory wall shear stress correlatespatially with early atherosclerosis? A systematic review. Cardiovascular Research, 99(2), 242–250(2013) |
Appendix A1
 2014, Vol. 35
2014, Vol. 35































