2014, Vol. 35
The Chinese Meteorological Society
Article Information
- Ai- feng WANG, Ming-kang NI 2014.
- Contrast structure for singular singularly perturbed boundary value problem
- Appl. Math. Mech. -Engl. Ed., 35 (5) : 655–666
- http: //dx. doi. org/10.1007/s10483-014-1819-7
Article History
- Received 2013-08-27;
- in final form 2013-11-16
2 Department of Mathematics, East China Normal University, Shanghai 200062, P. R. China
1 Introduction
Singular singularly perturbed problems can be found in chemical kinetics[1] ,semiconductor device[2, 3] ,Poisson-Nernst-Planck system[4],etc.,and have gained many mathematicians’ attention. In the work by Vasil'eva and Butuzov[3],the initial value problem and a special structure boundary value problem of singular singularly perturbed systems are considered by the boundary function method. A general singular singularly perturbed boundary value problem was examined by Schmeiser[2] using the same method as Vasil’eva. Within the framework of geometric singulary perturbation theory,Liu[4] studied the steady-state Poisson-Nernst-Planck system. There were many other studies on the singular singularly perturbed boundary value problem[5, 6, 7, 8] ,which considered the phenomenon of the boundary layer by the boundary function method or numerical method. However,the study on the contrast structure for the singular singularly perturbed problem is seldomly discussed in a relevant literature. When the reduced system has several isolate roots and the solution of the original problem approaches different reduced roots in different time,the contrast structure occurs. The contrast structure in singularly perturbed problems is mainly classified as a step-type contrast structure[9, 10, 11, 12, 13, 14, 15, 16, 17] or a spike-type contrast structure[18, 19] ,which corresponds to the heteroclinic orbit or homoclinic orbit in their phase space. A step-type contrast structure problem is only concerned in this paper . Its fundamental characteristic is that there is a t*(or multiple t*) within the domain of interest,which is called as an internal transition point. The position of t* is unknown in advance and needs to be determined thereafter. In the neighborhood of t*,the solution y(t,u) will have an abrupt structure change.
A singular perturbed boundary value problem
is studied[5] ,where a(x,y,t) keeps the sign unchanged.
Let μdy/dt = z. Then,(1) can be written as an equivalent system of the form
Denote u = (x,y,z)T,v = (y,z)T,u( ∓)(t) = (x( ∓)(t),y( ∓)(t),z( ∓)(t))T,where z( ∓)(t) ≡ 0,and F(u,t,μ) = (z,a(x,y,t)z + μg(x,y,t)T. The Jacobian matrix of F with respect to v is
where a( ∓)(t) = a(x( ∓)(t),y( ∓)(t),t). This shows that (1) is a singular singularly perturbed problem with a slow variable x. Furthermore,there exists a matrix
such that
Further study shows that,if a(x,y,t) has different signs as t ∈ [0,1],this problem will have a construct structure. In this paper,we discuss the contrast structure for (1) with the boundary conditions given by
2 Construction of asymptotic expansion
H1 Suppose that a(x,y,t),g(x,y,t),and f(x,y,t) are sufficiently smooth for (x,y,t) in D,where D is a bounded domain in the (x,y,t) space.
H2 For each t ∈ [0,1],suppose that the reduced equation
has a solution x ( − ) (t),y ( − ) (t) which is satisfied with x ( − ) (0) = x0,y ( − )(0) = y0 and a solution x ( + ) (t),y ( + ) (t) which is satisfied with x ( + ) (1) = x ( − ) (1),y ( + ) (1) = y1.
Moreover, a(x ( − ) (t),y( − )(t),t) > 0,a(x ( + ) (t),y ( + ) (t),t) < 0,t ∈ [0,1].
Remark 1 If H1 and H2 hold,there maybe exists a contrast structure for Problems (1)-(2), but the phenomena of boundary layers cannot occur.
Let t* be the internal transition point which has the formal asymptotic expansion of the following form:
where tj (j = 0,1,· · · ) are constants to be determined. Consider the following two problems.
The left problem (t ∈ [0,t*]) is
The right problem (t ∈ [t*,1]) is
where 
and x(+) (1,μ) = x(−) (1,t*,μ).
Suppose that the asymptotic solution of (1) and (2) is composed of these two parts. In terms of the remark and the boundary function method,the formal asymptotic expressions of the left problem and the right problem are given by
and
respectively,where 
are the coefficients of regular terms,
are the coefficients
of internal transition terms,and 
By (6) and (8),we know that the component y(t,μ) is continuous at t*. In order to get a smooth solution with a step-type contrast structure from y(− )(t) to y(+)(t),the following connection condition
would hold.
In terms of the boundary function method,the zeroth-order regular terms 
satisfy
the following system:
and
By H2,
. Furthermore,
.
For the high order terms 
(j = 1,2,· · · ),we have the equations and their boundary
conditions as follows:
where
are determined functions. Here ,
Obviously,(12) and (13) are initial value problems. Therefore, exist.
Next,we give the equations and their conditions for determining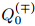 
u as follows:
By 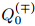x(∓∞) = 0,we obtain 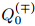x(τ) ≡ 0. (14) can be transformed into the following
system:
Let 
and 
. Then,(16) and (15) can be transformed into
By (17),we get
Integrating it from 0 to τ,we obtain
Let τ → ∓∞. Then,
Let
H3 Suppose that I(t0) = 0 is solvable with respect to t0 and I'(t0) ≠ 0.
To solve (16),we rewrite (16) as an equivalent system of the form
where
which is satisfied with
By using the linear transformation
(21)∓ can be written as the diagonal form
where
We obtain that (23) satisfying ξ(∓) ( ∓ ∞) = 0 and η(∓) ( ∓ ∞) = 0 is equivalent to the integral equations
Replaced by 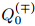y and 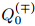z,(24) becomes
It follows from (22) and the successive approximation method that there is a unique solution
to (25) fo r s ufficiently s ma ll Q (0∓)z(0). Thus,
(27)− is an analytical representation of a stable invariant manifold of (21)− ,and (27)+ is an analytical representation of a stable invariant manifold of (21)+. Obviously,
By the inverse function theorem,(27) ∓ has a unique inverse function 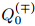z(0) = P( ∓) (
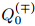y(0)) in the neighborhood of 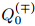y(0) = 0. Let Ω−⊂ R be the maximum domain of P(−) and
Ω+ ⊂ R be the maximum domain of P(+) .
H4 Suppose that 
,and
.
Lemma 1 Suppose that H1−H4 hold. Then,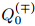u(τ) exist and satisfy the following
in equalities:
where C and γ are positive constants.
For the high order terms (j = 1,2,· · · ),we have the equations and their boundary
conditions as follows:
and
where 
,and 
take their values at
,and
take their values at 
. 
are the
known functions depending on 
(i = 0,1,· · · ,j − 1),and they satisfy the exponential
decay. Integrating (28),we can obtain 
. 
are known functions depending only
on 
(i = 0,1,· · · ,j) and 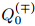z.
Problems (29) and (30) are the linear boundary value problems. Therefore,it is not difficult to verify that their solutions are
where
Φ(∓) (τ) and Ψ(∓) (τ) are the solutions of the matrix initial value problems
and
respectively. It is easy to prove H(∓) (τ) →a(∓) (t0) as τ → ∓∞. Moreover,H(∓) (τ) satisfy the Reccati equations,i.e.,
which plays a key role in matrix diagonalizations. It is therefore to get the estimate
where k is a positive constant.
Lemma 2 Suppose that H1−H4 hold. Then, (j = 1,2,· · · ) exist and satisfy the
following in equalities:
where C and γ are positive constants.
So far,we have already determined ,but only contained the unknown tj (j =
1,2,· · · ).
By 
,we get
Substituting them into
by H3,we have the coefficient of t1
Then,t1 is solvable. Similarly,tj can be calculated. So far,all the coefficients of the internal transition terms are determined. 3 Existence of step - type contrast structure
From Ref. [1],we obtain the existence of the solution for the left problem. It has the following asymptotic expansion:
Similarly,the solution to the right problem exists,and it has the following asymptotic expansion:
where
It is noted that t* is regarded as a parameter this time. It is not necessarily like the expansion
(4) of μ,where satisfy the equations and the boundary value conditions similar to
(14),(16),and (28)-(30),respectively. Here,we need to change t0 into t*.
Let
and
Then,
In (3 3 ),if we ta ke δ sufficiently large,μ sufficiently small,then,when δ takes different signs,
the right side of (33) has different signs. Thus,there exists
such that
H(t,μ) = 0. That is,
Thus,we have obtained a step-type contrast structure at the neighborhood of t with an internal transition layer as follows:
In summary,we have the following theorem.
Theorem 1 Suppose that H1−H4 hold. Then,there exists μ0 > 0 such that Problem s (1) and (2) have a step- type contrast structure as 0 < μ < μ0. Moreover,the following uniformly valid asymptotic expansion holds:
4 Example
In this section,an example is presented for how to construct a zeroth-order asymptotic solution with a step-like contrast structure.
The system is given by
According to the algorithm of this paper,we obtain that the reduced system
has a solution x( −)(t) = 12t2 − t + 1,y( −)(t) = t − 1,t ∈ [0,1],and the reduced system
has a solution x(+)(t) = 12t2 − t0 + 1,y(+)(t) = t,t ∈ [0,1].
Thus,
Obviously,−y (−)0(t) = 1 − t > 0,−y(+)0 (t) = −t <0. Thus,H2 holds. By (20),we get
which is the equation to determine t0. It is easy to obtain that t0 = 1/2. Then,H3 holds.
Moreover,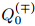x(τ) ≡ 0. For the zeroth-order terms 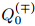y(τ) and 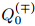z(τ),we have the
equations and their boundary conditions as follows:
and
Thus,
where
Obviously,as long as y0* ≠ ± 1/2,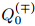
y(τ) and 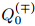z(τ) converge to zero exponentially.
| [1] | Vasil 'eva, A. B., Butuzov, V. F., and Kalachev, L.V. The Boundary Function Method for SingularPertubation Problems, SIAM, Philadephia (1995) |
| [2] | Schmesiser, C. and Weiss, R. Asymptotic analysis of singular singularly perturbed boundary valueproblems. SIAM Journal on Mathematical Analysis, 17, 560–579 (1986) |
| [3] | Vasil'eva, A. B. and Butuzov, V. F. Singularly Perturbed Equation in the Critical Case, Translatedas MRC-Technical Summary Report 2039, Mathematics Research Center, Madison (1980) |
| [4] | Liu, W. S. Grometric singular perturbation approach to steady-stable poisson-nernst-planck systems. SIAM Journal on Applied Mathematics, 65, 754–766 (2005) |
| [5] | Lin, W. Z. and Wang, Z. M. A singular singularly perturbed boundary value problem. Annals ofDifferential Equations, 12, 70–82 (1996) |
| [6] | Shi, Y. M. On singular singularly perturbed vector boundary value problems. Indian Journal ofPure and Applied Mathematics, 28, 679–695 (1997) |
| [7] | Zhu, H. P. The Dirichlet problem for a singular singularly perturbed quasilinear second orderdifferential system. Journal of Mathematical Analysis and Applications, 210, 308–336 (1997) |
| [8] | Kadalbajoo, M. K. and Aggarwal, V. K. Fitted mesh B-spline method for solving a class of singularsingularly perturbed boundary value problems. International Journal of Computer Mathematics,82, 67–76 (2005) |
| [9] | Vasil'eva, A. B. Contrast structures of step-like type for a second-order singularly perturbedquasilinear differential equation (in Russian). Zhurnal Vychislitel’noi Matematiki i Matematicheskoi Fiziki, 35, 520–531 (1995) |
| [10] | Vasil'eva, A. B. and Dovydova, M. A. On a contrast structure of step type for a class of secondorder nonlinear singularly perturbed equations (in Russian). Zhurnal Vychislitel’noi Matematikii Matematicheskoi Fiziki, 38, 938–947 (1998) |
| [11] | Vasil'eva, A. B. On systems of two singularly perturbed second order quasilinear equations (inRussian). Fundamentalnaya i Prikladnaya Matematika, 12, 21–28 (2006) |
| [12] | Vasil'eva, A. B. On some boundary-layer solutions of variable type for singularly perturbedparabolic equations (in Russian). Zhurnal Vychislitel’noi Matematiki i Matematicheskoi Fiziki,48, 651–659 (2008) |
| [13] | Ni, M. K. and Gurman, V. I. Realization of sliding modes as generalized solutions of optimalcontrol problems (in Russian). Avtomatica i Telemekhanika, 3, 51–59 (2008) |
| [14] | Ni, M. K. and Gurman, V. I. Representation of impulse regimes of generalized solutions of controlled differential systems (in Russian). Differential Equations, 44, 609–617 (2008) |
| [15] | Ni, M. K., Vasil'eva, A. B., and Dmitriev, M. G. On a steplike contrast structure for a problem ofcalculus of variations (in Russian). Zhurnal Vychislitel’noi Matematiki i Matematicheskoi Fiziki,44, 1271–1280 (2004) |
| [16] | Ni, M. K. and Wang, Z. M. On step-like contrast structure of singularly perturbed systems.Boundary Value Problems, 2009, 634324 (2009) |
| [17] | Ni, M. K. and Wang, Z. M. On higher dimensional contrast structure of singularly perturbeddirichlet problem. Science China, 55, 1–13 (2012) |
| [18] | Wang, A. F. and Ni, M. K. Spike-type contrast structures for a nonlinear singularly perturbedsecond-order equation (in Chinese). Acta Mathematica Scientia, 29A(1), 208–216 (2009) |
| [19] | Xie, F., Jin, Z. Y., and Ni, M. K. On the spike-type contrast structure of a second-order semilinear differential equation with integral boundary condition. Electronic Journal ofQualitativeTheory of Differential Equations, 62, 1–14 (2010) |