Shanghai University
Article Information
- Yan-hua WU, Hui-ying REN. 2014.
- Analysis of realistic rough surface for its globally dominant parameters using continuous wavelets
- Appl. Math. Mech. -Engl. Ed., 35(6): 741-748
- http://dx.doi.org/10.1007/s10483-014-1826-6
Article History
- Received 2013-7-4;
- in final form 2013-12-16
2. Hydrology Technical Group, Pacific Northwest National Laboratory, P.O. Box 999, Richland, WA 99352, U. S. A.
Engineering wall-bounded turbulent flows are significantly affected by the surface roughness conditions. Examples of these flows of practical interest include both external and internal flows such as those over turbine blades,aircrafts,marine vehicles,and through piping systems of heat exchangers. In most cases,the effects of surface roughness are detrimental. Rough surfaces can increase the skin friction and thus increase the energy consumption. They can also enhance the heat transfer rate at the wall,which will augment the thermal loading of the turbine blades and as a result reduce their lifetime. Thus,a clear and comprehensive understanding of how surface roughness affects the wall-bounded turbulent flows is imperative for both accurate modeling and successful control of these flows encountered in various engineering applications.
Unlike laboratory simulated roughness such as hemispheres and wire meshes,a typical rough surface in common engineering flows is more complex since the roughness elements are highly irregular in shape with random distribution which occupy a wide range of length scales,orienta- tion,and slopes. Since using realistic rough surfaces has been found to be absolutely necessary to accurately characterizing the physics of engineering turbulent flows,quite a few recent studies focus on investigating the effects of realistic roughness on various aspects of turbulent flows[1, 2, 3, 4, 5, 6, 7, 8]. Christensen and his coworkers[2, 3] analyzed realistic roughness by applying proper orthogonal decomposition (POD) in order to quantify the effects of different roughness scales on the tur- bulent flows. To overcome the inherent shortcomings of the POD method,Wu and Ren[7] usedthe multi-resolution analysis of discrete wavelet transforms to reconstruct a subset of the full rough surface. However,in these studies,only the simplified roughness models were obtained by either the POD method or the multi-resolution analysis,while the dominant topographical information regarding the roughness elements was not able to be provided.
Therefore,in this study,continuous Morlet and Mexican hat wavelets are used to estimate the dominant aspect ratio and orientation as well as the length scale of the roughness elements from a wide range of these randomly distributed spatial parameters in a highly irregular realistic surface topography. The identification of these salient parameters is important for the future studies of their impacts on the turbulent flows over this type of surfaces which are roughened by deposition of foreign materials.
2 Rough surfaceThe rough surface considered herein is generated from the profilometry measurements of a roughened turbine blade. The roughness of this particular surface is attributable to deposi- tion of foreign materials. Detailed description of this rough surface was provided by Wu and Christensen[1]. Figure 1 shows a contour plot of this highly irregular rough surface. The com- plex features of the current roughness are shown by the random distribution and a broad range of roughness parameters. It can be seen that the dominant features of this surface are elliptical in shape and are roughly aligned in the flow direction. However,the complexity of this surface is evident by random distribution and a broad range of length scales,orientation,and aspect ratios of the roughness elements.
 |
| Fig. 1 Contour of rough surface . |
Figure 2 presents the probability density function (pdf ) of the roughness amplitude about the mean elevation contrasted with a Gaussian distribution with an equivalent root mean square (RMS). It shows that the probability density function of this rough surface is not strictly Gaussian. Actually,as shown in Fig. 2,the roughness heights do not follow the Gaussian distribution.
 |
| Fig. 2 Probability density function of roughness amplitude about mean elevation where red dashed line shows Gaussian distribution with equivalent RMS value for comparison . |
The continuous wavelet transform (CWT) of a two-dimensional function f(x) is defined as the integral transform[9]
where W(a,b) is the wavelet coefficient,the overbar denotes complex conjugate,and represents a family of function termed wavelets which are generated by scaling and translation of the mother wavelet (x). In Eq. (2),a is the scale factor,b is the translation parameter,and the factor 1/a is for energy normalization across different scales so that The wavelet function (x) must have a zero mean to satisfy the admissibility condition and have compact support to obtain concentration in both space and scale domains. Two popular wavelets for the CWT are the Morlet and Mexican hat wavelets[9].The fully anisotropic Morlet wavelet devised by Neupauer and his coworkers[10, 11] is
where ko = (0,ko) is a wave vector with ko > 5.5 (ko = 2π in this study),and C is the rotation matrix given by A is the anisotropy matrix defined as and c is the normalization factor expressed by c = pL,which satisfies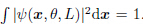 .
The matrix C rotates the entire wavelet through an angle θ w.r.t. the +x axis. Positive θ means
the rotation of the wavelet in the counter-clockwise direction. The matrix A makes the wavelet
anisotropic such that the ratio of the length of the wavelet in the direction perpendicular to θ
to that in the θ-direction is L. When L is less than 1,the wavelet is stretched in the θ-direction.
.
The matrix C rotates the entire wavelet through an angle θ w.r.t. the +x axis. Positive θ means
the rotation of the wavelet in the counter-clockwise direction. The matrix A makes the wavelet
anisotropic such that the ratio of the length of the wavelet in the direction perpendicular to θ
to that in the θ-direction is L. When L is less than 1,the wavelet is stretched in the θ-direction.
TheMexican hat wavelet is the second derivative of the Gaussian function. A two-dimensional anisotropic Mexican hat wavelet is given by[11]
where matrices C and A are the same as those in the Morlet wavelet.With the above anisotropic Morlet and Mexican hat wavelets,the wavelet coefficient W can be written to a function of the scale a,location b,orientation θ,and aspect ratio (or anisotropy ratio) L as follows:
This integral transform is performed to compute the wavelet coefficient,W(a,b,θ,L),for a range of scales,orientations,and aspect ratios in order to find the dominant features of the roughness elements in our highly irregular rough surface. Equation (8) is evaluated by the fast Fourier transform (FFT) since it can be considered as a correlation between f(x) and (x a ; θ,L). 4 ResultsCWTs using the above fully anisotropic Morlet and Mexican hat wavelets are performed on the current roughness topography without the mean elevation. The scalogram is computed from the wavelet coefficient expressed by
The range of the scale of a chosen in this study is 1 mm< a <45 mm for both the Morlet and the Mexican hat wavelets. This range of scale covers both small- and large-scale roughness elements since the grid spacing of the digitized roughness is about a quarter of a millimeter and the longest length of the roughness element is less than 40mm (see Fig. 1). The translation parameter b covers the whole domain of the rough surface. θ ranges from 0◦ to 20◦ with an increment of 1◦ since the roughness elements illustrate an positive angle to the +x axis and this angle is much less than 20◦. The aspect ratio L equals 1/N (N = 1,2,· · · ,8),which is used to account for the fact that the shape of the roughness is approximately elliptical with a longer axis roughly aligned in the flow direction (the +x direction).In principle,the scalogram,E(a,b,θ,L),can provide information about the dominant fea- tures of the roughness. However,it is difficult to analyze the scalogram directly since it is a five-dimensional function. In addition,since only the globally dominant roughness parameters are of interest in the present study,global functions based on the scalogram are used to analyze the current highly irregular roughness topography.
The scalogram,E(a,b,θ,L),is first integrated across the whole domain to yield a global function defined as[10, 11, 12]
This function provides useful information about the roughness elements with the dominant scale,orientation,and aspect ratio irrelevant to their locations.In order to find the dominant aspect ratio L,a function ηL(L) is computed by integrating η(a,θ,L) over all scales and orientation angles,i.e.,
Figure 3 presents ηL as a function of L for both the Mexican hat and Morlet wavelets. As shown in Fig. 3(a),the Mexican hat wavelet illustrates a dominant aspect ratio of L = 1 5 for the roughness elements. This aspect ratio is quite consistent with the general shape of theroughness elements presented in Fig. 1. In addition,ηL drops very quickly for L > 1 4 ,indicating that the roughness elements are quite elongated in the x-direction,which can be easily verified from the observation in Fig. 1. Further,it can be seen that the differences between the values of ηL for L < 1 4 are small,suggesting the existence of a rather wide range of aspect ratios,which is one of the facts illustrating the complexity of the rough surface studied herein. In contrast,the Morlet wavelet shows a monotonic decrease in ηL without identifying the largest aspect ratio. Therefore,the Morelet wavelet is not suitable to find the globally dominant L for the present roughness topography. |
| Fig. 3 ηL for Mexican hat wavelet and Morlet wavelet . |
As suggested by some past studies[10, 11, 12],a global function defined as
can be used as a better measure than η(a,θ;L) to be the dominant length scale. For a specific aspect ratio,ζa(a,θ;L) gives the relative energy distribution at different scales for a particular orientation w.r.t. the total energy at that orientation. This function provides information about the dominant length scales without inference on the dominant orientation. The relationship between the physical length scale of the roughness element,λ,and the wavelet scale,a,is λ π 3.6a for the Mexican hat wavelet and λ π a for the Morlet wavelet[11]. It is shown that only the Mexican hat wavelet illustrates a dominant aspect ratio of 1/5.Figures 4(a) and 4(b) present the contour plots of ζa(a,θ;L) for the Mexican hat and Morlet wavelets,respectively,with the dominant aspect ratio L of 1/5. It is seen that λ π 3.6a for the Mexican hat wavelet and λ π a for the Morlet wavelet. For the Mexican hat wavelet shown in Fig. 4(a),the function ζa gives two peak regions,i.e.,Region 1 for smaller peaks and Region 2 for larger peaks. In Region 1,the length scale is concentrated approximately on λ = 10mm for all orientations. The result in this region may reflect the length scales of newly generated small roughness elements. In Region 2,the dominant length scale increases gradually from λ π 54mm at small orientation angles to λ π 80mm at large angles. Since the majority of the individual roughness elements illustrate small orientation angles (see Fig. 1),it is believed that the scales at larger θ only reflect the length scale of the combination of two or more roughness elements at different locations along the z-axis. At small orientation angles,the Mexican hat wavelet analysis shows that the dominant scale is around 54mm,which is obviously too large when it is compared with the length of the majority of the individual roughness elements shown in Fig. 1. In contrast,the function ζa from the Morlet wavelet presents four regions of interest (see Fig. 4(b)). Regions I and II contain smaller peaks,while Regions III and IV contain larger peaks. Since Region III is concentrated only in large θ,it does not reveal scale information about the individual roughness elements as discussed above. Region IV is mostlyconfined within θ = 13◦,which is more consistent with the roughness topography. ζa drops to a significantly lower value outside Region IV when the scale is larger than 32mm,and then start increasing again for λ > 40mm. This trend illustrates that the higher bound of the length scale of the prominent individual roughness element is approximately 32mm,and ζa is attaining larger values due to the contribution of multiple elements when λ > 40mm. In addition,Region IV shows that the dominant length scale is around 24 mm while the lower bound of the length scale of the prominent roughness element is approximately 16mm. Referring back to Fig. 1,it can be seen that the above length scales obtained from the Morlet wavelet analysis are quite realistic. Coincidentally,this dominant length scale of 24mm obtained from the Morlet wavelet is approximately half of the length scale inferred by Region 2 (see Fig. 4(a)) from the Mexican hat wavelet analysis,which may indicate that the dominant length scale from the Mexican hat wavelet reflects that of the combination of two individual roughness elements in the x-direction. Smaller peaks of ζa in Region I imply the existence of some roughness elements about 8mm long at the orientations of 0◦-2◦. Similarly,the function ζa at Region II suggests the possibility of finding the roughness elements with the length scale of about 10mm at θ π 9◦. These small scale roughness elements may be considered to be newly generated from the deposition of foreign materials. Note that these small scales identified by the Morlet wavelet are approximately the same as those illustrated by Region 1 (see Fig. 4(a)) from the Mexican hat wavelet analysis.
 |
| Fig. 4 ζa with L = 1/5 for Mexican hat wavelet and Morlet wavelet . |
The function ζθ(θ,a;L) is defined as[10, 11, 12]
It is used to find the dominant orientation associated with the dominant aspect ratio and length scale. ζθ represents the relative energy distribution at different angles for a particular scale w.r.t. the total energy at that scale. Therefore,large values of ζθ indicate dominant orientations of the random roughness topography at a particular scale. Figures 5(a) and 5(b) present ζθ at λ = 24mm and L = 1/5 for the Mexican hat andMorlet wavelets,respectively. TheMexican hat wavelet gives the dominant orientation of 15◦ (see Fig. 5(a)),which is obviously too large. The Morlet wavelet shows a more realistic dominant angle of 4◦ with a range of possible orientations between 0◦ and 15◦ (see Fig. 5(b)). For θ > 15◦,ζθ obtained from the Morlet wavelet is essentially zero,indicating that there is no roughness element with the orientation larger than 15◦ at λ = 24mm and L = 1/5. Figure 5(b) shows that the majority of the roughness elements at λ = 24mm and L = 1/5 has angles less than 10◦,which is consistent with the observation from Fig. 1. The current results on the surface topography are also consistent with those on the anisotropic permeability data set studied by Neupauer et al.[11] where the Morlet wavelet was more effective than the Mexican hat wavelet at identifying the dominant length scales and orientations. |
| Fig. 5 ζθ at λ = 24mm and L = 1/5 for Mexican hat wavelet and Morlet wavelet . |
Finally,to verify that the dominant roughness parameters obtained above are reasonable, a comparison between some representative realistic highly irregular roughness elements and the ellipses generated from these parameters,i.e.,the length scale of 24mm,the aspect ratio of 1/5,and the orientation angle of 4◦,is presented in Fig. 6. It can be observed that these parameters indeed reasonably reflect the general geometric features of the roughness elements in this realistic roughness.
 |
| Fig. 6 Verification of dominant roughness parameters by comparing some representative roughness elements with ellipses generated using length scale of 24mm,aspect ratio of 1/5,and orien- tation angle of 4◦ . |
In this study,a continuous Mexican hat and Morlet wavelet analysis is performed on a highly irregular roughness topography to find the dominant aspect ratio,length scale,and orientation of the individual roughness elements out of a wide range of these parameters due to the com- plexity of the rough surface. The global measure ηL obtained from the Mexican hat wavelet analysis identifies that the dominant aspect ratio of the roughness elements equals 1/5. The dominant length scale and the orientation angle of the roughness elements are identified by the global functions,ζa and ζθ,from the Morlet wavelet to be 24mm and 4◦,respectively. These obtained parameters are quite consistent with the geometries of the roughness elements of the original roughness topography. Turbulence studies using the above globally dominant roughness parameters will be carried out later. Such turbulence studies will help to quantify the impact of the current highly irregular roughness by using a much simpler surface topography,based on which accurate modeling and successful control methods may be devised for engineering turbulent flows over such realistic rough surfaces in aerospace and power generation industries.
Acknowledgements This study is supported by Wright State University,Dayton,OH,U. S.A. The authors thank Professor K. T. CHRISTENSEN at University of Illinois at Urbana-Champaign for providing the roughness topography data.
| [1] | Wu, Y. and Christensen, K. T. Outer-layer similarity in the presence of a practical rough-wall topography. Physics of Fluids, 19, 085108 (2007) |
| [2] | Johnson, B. and Christensen, K. Turbulent flow over low-order models of highly-irregular surface roughness. AIAA Journal, 47, 1288-1299 (2009) |
| [3] | Mejia-Alvarez, R. and Christensen, K. Low-order representations of irregular surface roughness and their impact on a turbulent boundary layer. Physics of Fluids 22, 015106 (2010) |
| [4] | Wu, Y. and Christensen, K. T. Spatial structure of a turbulent boundary layer with irregular surface roughness. Journal of Fluid Mechanics, 655, 380-418 (2010) |
| [5] | Licari, A. and Christensen, K. Modeling cumulative surface damage and assessing its impact on wall turbulence. AIAA Journal, 49, 2305-2320 (2011) |
| [6] | Ren, H. and Wu, Y. Turbulent boundary layers over smooth and rough forward-facing steps. Physics of Fluids, 23, 045102 (2011) |
| [7] | Wu, Y. and Ren, H. On the impacts of coarse-scale models of realistic roughness on a forward-facing step turbulent flow. International Journal of Heat and Fluid Flow, 40, 15-31 (2013) |
| [8] | Wu, Y., Ren, H., and Tang, H. Turbulent flow over a rough backward-facing step. International Journal of Heat and Fluid Flow, 44, 155-169 (2013) |
| [9] | Daubechies, I. Ten Lectures on Wavelets, Society for Industrial and Applied Mathematics, Philadelphia (1992) |
| [10] | Neupauer, R. and Powell, K. A fully-anisotropic morlet wavelet to identify dominant orientations in a porous medium. Computers and Geosciences, 31, 465-471 (2005) |
| [11] | Neupauer, R., Powell, K., Qi, X., Lee, D., and Villhauer, D. Characterization of permeability anisotropy using wavelet analysis. Water Resources Research, 42, W07419 (2006) |
| [12] | Kumar, P. A wavelet based methodology for scale-space anisotropic analysis. Geophysical Research Letters, 22, 2777-2780 (1995) |
 2014, Vol. 35
2014, Vol. 35















