Shanghai University
Article Information
- Qing XIANG, Zheng-nan YIN. 2014.
- Investigation of temperature effect on stress of flexspline
- Appl. Math. Mech. -Engl. Ed., 35(6): 791-798
- http://dx.doi.org/10.1007/s10483-014-1829-6
Article History
- Received 2013-11-16;
- in final form 2014-1-4
Harmonic drive devices which consist of circular spline,flexible wheel,and wave generatorare widely used in aerospace,robotics,radar systems,general machinery,and other fields. Although harmonic gears in engineering applications are getting smaller and lighter,their geometric structures are becoming more and more complex and the corresponding working environments are tending harsher,which puts forward higher requirements for the harmonic gear structures. Especially,when a harmonic gear is working,the wave generator and inner surface of the flexspline produce heat because of friction. The temperature of the gear engagement region will usually rise by 40℃−50℃. In some extreme case,for instance,in the lunar exploration, the ambient temperature of the outside of the harmonic gear box may be about 130℃ or even higher. Meanwhile,the miniaturization of flexible wheel puts forward higher cooling requirements. As a result,the heat cannot be quickly spread out. Therefore,the study of the effect of the temperature on the stress of flexspline is important [1, 2] .
There are many researches focusing on the stress of flexspline [3, 4, 5, 6] ,but few of them con- siders the temperature effects on the stress of the flexspline. Matyushin and Kryzhanovskii [7] investigated the friction and wear in metallic and polymer pairs of harmonic gears,and used the harmonic gears with plastic links in the strength calculations and tests. Jeon and Oh [8] studied the stress,deformation,and vibration characteristics of the composite flexspline as a part of the speed reducer by the finite element method (FEM). They showed that composite flexspline showed an improved quality compared with conventional steel flexspline at natural frequency,stiffness,and damping capacity. Folega and Siwiec [9] studied the materials of flexible wheel,such as fiber-reinforced epoxy resin materials and carbon fiber reinforced materials,on its performance by a finite element analysis software. Li [10] and Vassileva et al. [11] studied the transmission performance of the solid and grease lubricated harmonic drivers under different temperatures and loading velocities. Priimakov and Rudnitskii [12] experimentally considered the additional temperature stresses when analyzing the stress-strain state of the flexspline. They found that the radial temperature deformation exerted a considerable effect on the en- gagement geometry of the flexspline and thus altered the form of the middle surface of the two-layered shell of the flexspline. Chen et al. [13] analyzed the harmonic gear’s temperature distribution in the static state under different working conditions. Based on the FEM,Kayabasi and Erzincanli [14] calculated the stress of the flexspline teeth,and obtained the improvement of the fatigue life by changing the shape of the tooth best. Chen et al. [15] simulated the contact stress and contact deformation of the harmonic gear in the assemble state and the transmission state,respectively,by the ANSYS software. Zhang and Yang [16] analyzed and compared the virtual modeling of the flexspline by the SolidWorks software,and provided a new method to design harmonic gear mechanism. He and Dong [17] and Pan et al. [18] calculated the flexspline stress coupled with the temperature effect by the ANSYS software. They [17, 18] found that the flexible wheel cylinder temperature had little effect on the flexspline stress,but the effect of the ring portion could not be ignored. Gao et al. [19] analyzed the effects of the variations of the key structure parameters,including the cylinder length,the gear thickness,the smooth cylindrical wall thickness,the tooth width,and the fillet radiuses of the three flexible gears,on the maximum equal stress of the flexible gear and smooth cylinder with the ANASY software. The coupling effect of heat and structure and the effect of temperature on the stress of the flexible gear were both analyzed with the simplified model.
In this paper,we consider the change of temperatures of the inner and outer surface of the flexspline according to the linear thermal elastic theory with heat transmission and thermoelastic coupling. Based on the geometric and mechanical characteristics of the harmonic gear, a circular thin shell model is presented. Then,the stress solution of the flexspline is derived for different temperature fields. With comparative discussion of the effects of the displacement loading and temperature loading on the stress of the flexspline,an impact factor formula,which reflects the effect of temperature on the stress of flexspline,is obtained. Finally,numerical calculations are carried out for the harmonic gear.
2 Model and equationsIn a harmonic gear (see Fig. 1),the deformed shape of the flexspline is determined by the wave generator. Different deformed shapes have different effects on the working capacity. Here, we use the same two-wave generator as that used in Ref.[3] as shown in Fig. 1,where the mechanical process of the wave generator to the flexspline can be treated as a two concentrated force model. The deformation diagram of the flexspline is shown in Fig. 2,where the solid curve is the shape after deformation which is determined by the two concentrated forces added by the wave generator,and the dashed curve is the original shape of the flexspline. In Fig. 2,w is the radial displacement of the flexspline at any point,w 0 is the maximum radial displacement of the flexspline,R is the basic radius of the flexspline,θ is the angle between the radial displacement and the flexspline long axis,and ρ is the distance from the central point to the flexible wheel. As shown in Fig. 2,

 |
| Fig. 1 Sructural diagram of harmonic gear |
 |
| Fig. 2 Displacement diagram of flexspline where solid line is deformed orbit of flexspline and dashed line is datum orbit of flexspline |
When a harmonic gear is working,the temperature of the gear will rise because of the heat accumulation due to friction. The temperature field distribution of the flexspline is related not only with the heat absorption but also with the deformation [20] .
Generally,the heat conduction equation is
where k is thermal conductivity,T is temperature,ρ is the density,T0 is the reference temper- ature,a is the thermal expansion coefficient,c is the specific heat,t is the time,e is the volume strain,λ and μ are Lame constants,and ▽2 is the Laplacian operator.The equations of motion is
where G is the shear modulus,and β is the coefficient of the thermal stress.The last term on the right side of Eq.(1) is the coupling term,which means that heat transformation in elastic body not only can cause the temperature rise but also can partly make the elastic body deform. In other words,the temperature field cannot be determined by heat transformation independently,but must be derived with the solutions of the motion equations simultaneously [20] .
If the coupling coefficient is very small or the deformation is relatively slow,the coupling effect can be neglected [21] . Due to the fact that the coupling effect is related to the deformation rate,the coupled dynamic problem can be treated by the heat transmission equation and the motion equation [20, 21] . Therefore,this paper can use the heat transmission equation to calculate the temperature field and use the motion equation to calculate the displacement field.
2.2 Flexspline stress under force loadingSince the thickness of the shell of a flexspline is far smaller than its radius,with appropriate assumptions and simplifications,it can be treated as a thin circular shell theoretically.
It has been shown that the bending stress is the main stress component in the flexible wheel [2, 3, 4, 5, 6, 7] . Therefore,to obtain the flexspline strength,we only need to calculate the maximum bending stress in the two concentrated force model.
The radial displacement w can be expressed as
The maximum bending moment of the flexspline is The maximum bending stress of the flexspline is where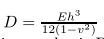 is the bending stiffness,E is the elastic modulus,h is the thickness of the
flexspline,and v is Poisson’s ratio.
2.3 Flexspline stress under temperature loading
is the bending stiffness,E is the elastic modulus,h is the thickness of the
flexspline,and v is Poisson’s ratio.
2.3 Flexspline stress under temperature loading
According to Refs.[16, 17],the effect of temperature can be investigated by assuming the flexspline as a cylindrical shell where the gear-tooth end is free and the other end (x = L) is fixed. Establish a coordinate shown in Fig. 3. According to the axisymmetric thermoelastic bending differential equation of the cylindrical shell [21] ,
 |
| Fig. 3 Thermal stress coordinate system |


Suppose that one side has no effect on the other side,i.e.,C1 = C2 = 0. Since C3 ,C4 ,and wp can be obtained for different temperature fields,the flexspline thermal bending deflection equation can be determined.
Considering that the temperature varies linearly from the outer surface to the inner surface of the shell,for a long flexible wheel,neglecting the effects of the boundary condition on the other side,we can obtain the radial displacement according to Ref.[21] as follows:
where T1 and T2 are the temperatures of the outer surface and the inner surface,respectively.When x = 0,the bending moments of the flexspline are
The internal forces are The corresponding axial bending stress is The circumferential bending stress is 3 Results and discussion 3.1 Theoretical results Theoretical calculations are carried out for the flexspline gear by the aforementioned theoretical model. For the calculation,we choose the values of the required parameters as follows [17] :
Substituting the above values into Eqs.(5) and (13),we can obtain the maximum bending stress of the flexspline at z = ±h/2 to be 120.0MPa and the maximum circumferential bending stress at z = ±h/2 to be 46.4MPa. The ratio of the maximum circumferential bending stress to the maximum bending stress is 38.7%. This means that the effect of the temperature changes on the flexspline stress is significant,and it cannot be ignored.
From Eqs.(5) and (13),we can get the temperature factor expressed by

In order to verify the results in Section 3.1,some numerical calculations are carried out with the ANSYS software. The results are shown in Figs.4-7.
 |
| Fig. 4 Effects of temperature load on maximal bending stress |
 |
| Fig. 5 Effects of length on temperature stress with R = 60mm and L = 72mm |
 |
| Fig. 6 Effects of thickness on temperature stress with R = 60mm and L = 72mm |
 |
| Fig. 7 Effects of radius on temperature stress with h = 1.74mm and L = 72mm |
Figure 4 shows the maximal bending stress obtained by Eq.(5) with the above parameters listed in Section 3.1 and different temperature loads. It can be seen that the maximal bending stress varies linearly with the temperature loads,which means that the temperature effects on the maximal bending stress of the flexspline cannot be ignored.
Meanwhile,we can infer that the values of the finite element results are generally larger than those of the theoretical results. This is because that the theoretical calculation does not consider the thickness and length of the flexspline. Therefore,this paper considers the effects of the thickness and length of the flexible wheel on the calculated stress during the following calculations.
Fig. 5,Fig. 6,Fig. 7 investigate the effects of the wheel length of the flexspline,the radius of the flexspline,and the thickness of the flexspline on the thermal stress with and without temperature loads. Here,we assume that the flexspline is under two concentrated forces at both ends. The results show that the obtained stresses with temperature loads are larger than those without temperature loads. Moreover,the obtained stress increases with the increase in either the wheel length or the thickness of the flexspline,while decreases with the increase in the radius of the flexspline.
4 ConclusionsWith investigation of the stress of a harmonic gear flexspline involving the effects of temperature,the following conclusions can be drawn:
(1) The temperature difference between the inner surface and the outer surface of the flexspline has significant effects on the stress. When the temperature difference between the inner surface and the outer surface is 20℃,the stress varies more than 30%.
(2) The obtained stress increases with the increase in either the wheel length or the thickness of the flexspline,while decreases with the increase in the radius of the flexspline.
| [1] | Wand, C. M., Yang, P., and Zhang, L. Y. Summary of status on the harmonic gear driving technology. Journal of Mechanical Transmission, 30, 86-88 (2006) |
| [2] | Baumgartner, E. T., Bonitz, R. G., Melko, J. P., Shiraishi, L. R., and Leger, P. C. The Mars exploration rover instrument positioning system. Aerospace Conference, 2005 IEEE, Big Sky, Montana (2005) |
| [3] | Shen, Y. W. and Ye, Q. T. Theory and Design of the Harmonic Gear Drive (in Chinese), China Machine Press, Beijing (1985) |
| [4] | Oguz, K. and Fehmi, E. Shape optimization of tooth profile of a flexspline for a harmonic drive by finite element modeling. Materials and Design, 28, 441-447 (2007) |
| [5] | Ostapski, W. and Mukha, I. Stress state analysis of harmonic drive elements by FEM. Bulletin of the Polish Academy of Sciences, 55, 115-123 (2007) |
| [6] | Ostapski, W. Analysis of the stress state in the harmonic drive enerator-flexspline system in relation to selected structural parameters and manufacturing deviations. Bulletin of the Polish Academy of Sciences, 58, 683-698 (2010) |
| [7] | Matyushin, E. G. and Kryzhanovskii, V. K. Friction and wear in metallic and polymer pairs of harmonic gears. Izvestiya Vysshikh Uchebnykh Zavedenii, Mashinostroenie, 2, 25-30 (1974) |
| [8] | Jeon, H. S and Oh, S. H. A study on stress and vibration analysis of a steel and hybrid flexspline for harmonic drive. Composite Structures, 47, 827-833 (1999) |
| [9] | Folega, P. and Siwiec, G. Numerical analysis of selected materials for flexsplines. Archives of Metallurgy and Materials, 51, 185-191 (2012) |
| [10] | Li, B. Orthogonal experiment analysis on transmission performance of space lubricated harmonic drive. Journal of Mechanical Engineering, 48, 82-87 (2012) |
| [11] | Vassileva, D., Kiyosawa, Y., and Suzuki, M. Sensorless torque control for a robot with harmonic drive reducers. Mechanics Based Design of Structures and Machines, 39, 253-267 (2011) |
| [12] | Priimakov, A. G. and Rudnitskii, V. I. Experimental determination of temperature deformations of metal-polymer flexible wheels in harmonic transmissions. Soviet Engineering Research, 7, 9-11 (1987) |
| [13] | Chen, J., Wang, J. X., Ma, L., and Wang, H. Static analysis of filter reducer considering the thermal field effect (in Chinese). Machinery Design & Manufacture, 12, 10-12 (2012) |
| [14] | Kayabasi, O. and Erzincanli, F. Shape optimization of tooth profile of a flexspline for a harmonic drive by finite element modeling. Materials and Design, 28, 441-447 (2007) |
| [15] | Chen, X. X., Lin, S. Z., and Xing, J. Z. Modeling of flexspline and contact analyses of harmonic drive. Key Engineering Materials, 419, 597-600 (2010) |
| [16] | Zhang, R. and Yang, J. J. Virtual modeling and finite element analysis of flexspline based on solidworks. Applied Mechanics and Materials, 86, 218-221 (2011) |
| [17] | He, W. and Dong, H. J. Flexspline stress analysis considering thermal field effect by FEM (in Chinese). Mechanical Science and Technology for Aerospace Engineering, 28, 955-959 (2009) |
| [18] | Pan, F., Dong, H. J., and Ge, W. J. Backlash analysis on the harmonic wave gear transmission under extreme environment (in Chinease). Journal of Machine Design, 27, 58-62 (2010) |
| [19] | Gao, H. B., Li, Z. G., and Deng, Z. Q. Sensitivity analysis of cup-shaped flexible gear parameters to its stress based on ANSYS. Journal of Mechanical Engineering, 46, 1-7 (2010) |
| [20] | Fan, X. J. and Chen, G. G. On coupling theory of thermoelasticity (in Chinese). Mechanics Advances, 12, 339-345 (1982) |
| [21] | Yan, Z. D. and Wang, H. L. Thermal Stress (in Chinese), Higher Education Press, Beijing (1993) |
 2014, Vol. 35
2014, Vol. 35















