Shanghai University
Article Information
- B. AMIRIAN, R. HOSSEINI-ARA, H. MOOSAVI. 2014.
- Surface and thermal effects on vibration of embedded alumina nanobeams based on novel Timoshenko beam model
- J. Meteor. Res., 35(7): 875-886
- http://dx.doi.org/10.1007/s10483-014-1835-9
Article History
- Received 2013-3-13;
- in final form 2014-1-14
2. Department of Mechanical Engineering, Payame Noor University, Tehran 19395-3697, Iran
The performance and reliability of micro- and nano-electromechanical systems have increas- ingly become a hot research area for many engineers and material scientists in recent years. The alumina (Al2O3) is a chemical material that is widely used for reinforced nanobeams,especially for nanowires such as sensors,probes,actuators,transistors,and resonators in nano-electro- mechanical systems[1, 2]. In the design of nanobeams,it is of great importance to acquire the dynamic behaviors accurately. Thus,for nanoscale materials and structures,the surface ef- fects become significant due to the high ratio of surface area to volume. The atomistic and experimental simulations reveal that the ratio of surface to volume plays an important role in nanoscale problems[3]. Gurtin and Murdoch[4] and Gurtin et al.[5] established the surface elasticity theory and its applications in nanosized structural element which agreed reasonably well with experimental measurements[6, 7, 8, 9]. Wang et al.[10] investigated the effects of surface tension on the elastic properties of nanostructures. They concluded that the effective Young’s modulus of Al nanowires was significantly affected by the surface tension. Wang[11] considered the transverse vibration of fluid-conveying nanotubes. Assadi and Farshi[12] also investigated the size-dependent stability and self-stability of circular nanoplates. Zang and Zhao[13] re- viewed a diffusion and curvature dependent surface elastic model in lithium ion battery. They demonstrated that the nanostructured electrode with suitable structure and size would be self- strengthened by the surface stresses. Karabalin et al.[14] studied the nonlinear dynamics of two elastically coupled nanomechanical resonators and demonstrated that one oscillator could be modified by driving the second oscillator. Gheshlaghi and Hasheminejad[3] reported the surface effects on nonlinear vibration of nanobeams. They concluded that by increasing the nanobeam’s dimensions,all natural frequencies gradually approached the nonlinear Euler-Bernoulli beam limit,which entailed an expected decrease in the surface effects. Wang and Zhao[15] presented thermo-hyperelastic models for nanostructured materials. They concluded that the residual stress should not be neglected for large surface residual stress and very small characteristic length. Wang and Wang[16] also studied the surface effects on the vibration and buckling of double-nanobeam system. Their results showed that both surface elasticity and residual surface tension could affect the natural frequency. In fact,critical loads and surface effects have the same impact in three deformation modes.
Most of these previous studies treated a nanowire as a simple Euler beam and neglected the effects of transverse shear deformation and rotary inertia. Therefore,the Timoshenko beam the- ory has been employed to analyze the axial buckling[17, 18] and free vibration of nanobeams[19]. Abbasi et al.[20] reported the exact solution of the dynamic coupled thermo-elastic response of Timoshenko beams. Wang and Feng[21] investigated the axial buckling and transverse vibration of nanowires based on the Timoshenko beam model. They found that the surface effects with positive surface constants would tend to increase the critical axial force and natural frequencies. A new approach for beams resting on the Pasternak elastic foundation was presented by Lu et al.[22]. Furthermore,Zhu et al.[23] reported the effects of surface and initial stresses on bending stiffness of nanofilms.
In addition,the necessity to work in high temperature conditions requires the consideration of thermal effects in dynamic behavior of nanobeams. Hence,Liu et al.[24] studied thermo- electro-mechanical vibration of piezoelectric nanoplates. In their research,the piezoelectric nanoplates were subjected to a uniform temperature change. Moreover,Shariyat[25] investi- gated the dynamic buckling of piezo-laminated plates under thermo-electro-mechanical loads with consideration of the temperature dependency of the material properties. Komijani et al.[26] investigated vibration of thermo-electrically post-buckled rectangular functionally graded piezo- electric beams. Therefore,it is clear that the consideration of thermal effects in vibration of nanowires is absolutely essential and should not be ignored.
The present study is concerned with the derivation of the governing equations for vibration of anodic alumina nanobeams modeled as the refined Timoshenko beam theory. The influences of the surface and thermal effects along with Winkler and Pasternak foundation moduli,the diameter of nanobeams,the aspect ratio,and the vibration modes on free vibration of the nanobeams are discussed in detail. The effects of transverse shear deformation and rotary inertia are also considered in this model. The surrounding elastic medium is described to be of the Winkler- and Pasternak-type. To this end,Hamilton’s principle is employed to derive the governing equations and corresponding boundary conditions,and a direct technique is then used to obtain the natural frequency of nanobeams with immoveable supports.
2 Surface elasticity effectThe creation of a free surface leads to excess free energy and the molecules near a free surface experience a different local environment condition as compared with the internal molecules.Thus,the surface effects on the mechanical behavior of nanosized elements and nanomaterials can be examined by considering the surface energy or surface stresses. According to Gibbs[27] and Cammarata[28],the surface stress tensor,σαβS,is related to the surface energy density, , through the surface strain tensor,σαβSby
For the deformation of nanobeams,only the surface stress and the surface strain along the longitudinal direction are important,and the one-dimensional and linear form is where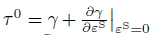 is the residual surface stress when the bulk is under unstrained condi-
tion,and ES is the surface Young’s modulus. The ratios of the surface energy,the surface stress,
and the surface modulus to the bulk elastic modulus are usually on the order of nanometers.
3 Formulations
is the residual surface stress when the bulk is under unstrained condi-
tion,and ES is the surface Young’s modulus. The ratios of the surface energy,the surface stress,
and the surface modulus to the bulk elastic modulus are usually on the order of nanometers.
3 Formulations
Based on the classical Timoshenko beam theory,the displacement field equations are ex- pressed as
where u(x,y,z,t) and w(x,y,z,t) are the axial and transverse displacements of the point (x,0) on the mid-plane (i.e.,z = 0) of the beam,and '(x,t) denotes the rotation of the cross-section beam. The nonzero strains according to the Timoshenko beam theory are expressed as where "xx and "xz are the axial and shear strains,respectively. In the refined Timoshenko beam theory,the bending moment M and the shear force Q are given by where G is the shear modulus,A is the cross sectional area,E is Young’s modulus of the bulk,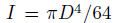 is the cross section moment of inertia,and KS is the shear correction factor to
compensate the error due to the constant shear stress assumption in the Timoshenko beam
theory. The shear coefficient for a circular cross section beam is expressed as[29]
where ν is Poisson’s ratio,and (EI)* is the effective flexural rigidity which is given as follows:
and ES is the effective Young’s modulus which can be determined either by atomic simula-
tions or experimental measurements. The contribution of the residual surface tensions on the
lower and upper surfaces of the nanobeam can be introduced through the effective transversely
distributed loading along the nanobeam longitudinal direction,q(x),in the form of[30]
where H is a constant parameter which is determined by the nanobeam’s cross sectional area
and residual surface tension along the nanobeams as follows[30]:
For circular cross section,we use
is the cross section moment of inertia,and KS is the shear correction factor to
compensate the error due to the constant shear stress assumption in the Timoshenko beam
theory. The shear coefficient for a circular cross section beam is expressed as[29]
where ν is Poisson’s ratio,and (EI)* is the effective flexural rigidity which is given as follows:
and ES is the effective Young’s modulus which can be determined either by atomic simula-
tions or experimental measurements. The contribution of the residual surface tensions on the
lower and upper surfaces of the nanobeam can be introduced through the effective transversely
distributed loading along the nanobeam longitudinal direction,q(x),in the form of[30]
where H is a constant parameter which is determined by the nanobeam’s cross sectional area
and residual surface tension along the nanobeams as follows[30]:
For circular cross section,we use 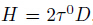 ,where D is the diameter of the nanobeam. The
equations of motion of nanobeams embedded in an elastic medium can be derived based on
Hamilton’s principle as follows:
where K,U,and V are the kinetic energy,the strain energy,and the potential energy,respec-
tively. Now,by implementing the relations (2),(5),(6),and (11) into Eq. (13),the equilibrium
conditions of forces and moments are obtained as follows:
The mass inertia m0 and m2 are defined by
In Eq. (14),Pτf is the density of reaction force of elastic foundation,and is defined as
where KW and KP represent the Winkler and Pasternak moduli (the shear layer foundation
stiffness) of the elastic medium,respectively. Here,N represents the axial force on the nanobeam
and is represented as
where Nm is the axial force due to the mechanical loading prior to buckling,and Nθ is the axial
force due to the influence of temperature changes. It is noted that at higher temperature,the
values for Young’s elasticity modulus are lower than those at lower temperature. However,at
different applied temperatures,the values of Young’s modulus are nearly equal. Furthermore,
experiments show that this modulus is not changed until 800 ◦C[31]. In addition,Jayaseelan et
al.[32] concluded that the mechanical properties of porous alumina are independent of tempera-
ture changes. Therefore,we assume that the mechanical properties of alumina nanobeams are
constant with the change of temperature. As a result,the theory of thermal elasticity mechanics
is adopted,and Nθ is given by
where ax is the coefficient of thermal expansion in the direction of the x-axis,ν is Poisson’s
ratio,and θ denotes the change in temperature. By considering the boundary conditions for
immoveable supports,the axial force due to mechanical loading will be zero.
By using the separation of variables,we can assume trigonometric solutions for vibration
analysis of circular nanobeams in the form of
,where D is the diameter of the nanobeam. The
equations of motion of nanobeams embedded in an elastic medium can be derived based on
Hamilton’s principle as follows:
where K,U,and V are the kinetic energy,the strain energy,and the potential energy,respec-
tively. Now,by implementing the relations (2),(5),(6),and (11) into Eq. (13),the equilibrium
conditions of forces and moments are obtained as follows:
The mass inertia m0 and m2 are defined by
In Eq. (14),Pτf is the density of reaction force of elastic foundation,and is defined as
where KW and KP represent the Winkler and Pasternak moduli (the shear layer foundation
stiffness) of the elastic medium,respectively. Here,N represents the axial force on the nanobeam
and is represented as
where Nm is the axial force due to the mechanical loading prior to buckling,and Nθ is the axial
force due to the influence of temperature changes. It is noted that at higher temperature,the
values for Young’s elasticity modulus are lower than those at lower temperature. However,at
different applied temperatures,the values of Young’s modulus are nearly equal. Furthermore,
experiments show that this modulus is not changed until 800 ◦C[31]. In addition,Jayaseelan et
al.[32] concluded that the mechanical properties of porous alumina are independent of tempera-
ture changes. Therefore,we assume that the mechanical properties of alumina nanobeams are
constant with the change of temperature. As a result,the theory of thermal elasticity mechanics
is adopted,and Nθ is given by
where ax is the coefficient of thermal expansion in the direction of the x-axis,ν is Poisson’s
ratio,and θ denotes the change in temperature. By considering the boundary conditions for
immoveable supports,the axial force due to mechanical loading will be zero.
By using the separation of variables,we can assume trigonometric solutions for vibration
analysis of circular nanobeams in the form of 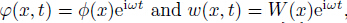 ,where
Φ(x) and W(x) are the mode shapes and ! is the frequency of natural vibration[33]. Therefore,
substituting '(x,t) and w(x,t) into Eqs. (14) and (15),we obtain
Towards eliminating Φ from Eqs. (21) and (22),we solve Eq. (21) for dΦ
dx . Differentiating Eq. (21)
once and substituting for dΦ
dx ,we obtain
Consider the boundary conditions for simply-supported nanobeams with immoveable ends as
follows:
Then,the general solution can be considered as follows:
The above solution can satisfy all boundary conditions. Substituting this solution into Eq. (23),
one can obtain
4 Results and discussion
,where
Φ(x) and W(x) are the mode shapes and ! is the frequency of natural vibration[33]. Therefore,
substituting '(x,t) and w(x,t) into Eqs. (14) and (15),we obtain
Towards eliminating Φ from Eqs. (21) and (22),we solve Eq. (21) for dΦ
dx . Differentiating Eq. (21)
once and substituting for dΦ
dx ,we obtain
Consider the boundary conditions for simply-supported nanobeams with immoveable ends as
follows:
Then,the general solution can be considered as follows:
The above solution can satisfy all boundary conditions. Substituting this solution into Eq. (23),
one can obtain
4 Results and discussion
The surface effects on nanobeams under thermal field and embedded in two-parameter elastic foundation are discussed and modeled based on a refined Timoshenko beam theory. In order to review the effects of various parameters with consideration of surface elasticity,we consider the material properties of an anodic alumina nanobeam with the crystallographic direction of (111)[6]. Therefore,Young’s modulus E = 70 GPa,Poisson’s ratio ν = 0.3,the mass density ρ = 2 700 kg/m3,αx = 8.4×10−6 K−1,the surface properties ES = 5.188 2 N/m,and τ = 0.910 8 N/m are applied in the analysis.
To validate the present approach for vibration of nanobeams with consideration of surface effects,the results obtained from Eq. (27) are compared with those obtained by Ref. [21]. In Ref. [21],the nanobeam is assumed as a silver nanowire with a circular cross section. An aspect ratio of L/D = 5 is taken for the comparison. The frequency ratios of Mode 1 against different diameters are illustrated in Fig. 1.
 |
| Fig. 1 Comparison of natural frequencies with consideration of surface effects for different Timo- shenko beam models . |
Here,!1 is the natural frequency of the first mode calculated by the Timoshenko beam model,and !E is the natural frequency of the first mode predicted by the classical Euler beam model. In fact,it is concluded that the present results are found to be in good agreement as compared with the literature. Furthermore,it can be seen that increasing the diameter plays an important role in the vibrations of nanobeams.
The surface effects on the natural frequency of nanobeams are shown in Fig. 2. The diam- eters of nanobeams are assumed to be 5 nm,10 nm,and 20 nm. The Winkler and Pasternak parameters,the axial compressive force,and the rotary inertia effects are neglected. It is clear that with the increase in the aspect ratio,the natural frequencies decrease. In the presence of surface effects,the natural frequencies increase in comparison with the case of classical Timo- shenko beam. Moreover,when the diameter of the nanobeam increases,the natural frequencies significantly reduce. It is observed that the natural frequencies of the circular nanobeam with consideration of surface effects and a small diameter (D = 5 nm) are strongly affected by the aspect ratio in comparison with the circular nanobeam with the classical Timoshenko theory and a large diameter (D = 20 nm). Therefore,the surface effects play an important role in determination of the natural frequencies. As can be seen,the critical natural frequency occurs when L/D = 4,and the lowest possible ! occurs at D = 20 nm with the assumption of the classical theory.
 |
| Fig. 2 Variation of natural frequency versus aspect ratio in presence of surface effects . |
In the absence of two-parameter elastic foundation and thermal effect,we consider the effect of the Winkler modulus on the governing equation. In Fig. 3,the effect of the Winkler foundation on the natural frequency in the presence of surface effect is illustrated. The values of D = 10 nm and D = 20 nm are taken for the diameter of nanobeams. It is concluded again that with the increase in the aspect ratios,the natural frequencies decrease. It is noted that the frequencies with consideration of the Winkler modulus are higher than its counterpart without elastic foundation. This means that the Winkler parameter leads to the increase in the natural frequencies,but this increment is not considerable. Moreover,with the increase in the Winkler constant,the natural frequencies decrease,because the increase in the Winkler modulus causes the nanobeams to be more rigid. In addition,when the surface effect is taken into account, the natural frequencies increase in comparison with the classical Timoshenko beam model. The effect of large diameters on natural frequencies is also illustrated in Fig. 3. It is clear that the effect of large diameter leads to significant reduction in values of natural frequencies. Natural frequencies for circular nanobeams with lower Winkler parameters (e.g.,KW = 8 × 104 N/m2) are significantly affected by the aspect ratio in comparison with higher Winkler modulus (e.g., KW = 4 × 106 N/m2). As can be shown,the natural frequencies in the case of classical theory are less than its counterpart with surface effects,but unlike the previous case,the difference between classical and present model with surface effect is minimal.
 |
| Fig. 3 Variation of natural frequency with aspect ratio for large diameters in presence of surface effects . |
In addition,we illustrate the variation of natural frequencies with two-parameter elastic medium with consideration of surface effects as compared with the classical Timoshenko theory. A value of KW = 102 N/m2 is taken for the Winkler parameter.
Figure 4 shows the effect of Pasternak foundation on the natural frequency of nanobeams in the absence of thermal field. In this case,we assume that KW is constant and KP is considered for four different values.
 |
| Fig. 4 Variation of natural frequency with Pasternak foundation for different aspect ratios (KW = 102 N/m2 and m = 1) . |
It is illustrated in Fig. 4 that the Pasternak foundation leads to a significant increase in the natural frequencies as compared with the Winkler modulus. Similar to previous results, with the increase in the aspect ratio,natural frequencies decrease,but with the increase in the shear modulus parameter,natural frequencies increase. With regard to surface effects,the natural frequencies increase as compared with the classical theory. It is noted that the difference between frequencies in the absence and presence of surface effects is more obvious. Also,the effect of large diameter on natural frequencies of nanobeams is investigated in Fig. 4. It is concluded that by increasing the nanobeam’s diameter,according to Eq. (10),the impact of surface effects is more sensible,and the natural frequencies decrease. Moreover,increasing the Pasternak modulus leads to the increase in the frequencies. In addition,the natural frequencies obtained from the classical Timoshenko beam model are less than their counterparts with surface effects. Therefore,the diameter of nanobeams plays an important role in natural frequencies together with surface effects and leads to an increase in the distributed force due to the residual surface stresses.
In Fig. 5,we discuss the thermal effects on natural frequencies in the presence of the surface effects. It is noted that temperature changes vary over the range of 20 ◦C-100 ◦C,and according to previous discussions,the mechanical properties of alumina nanobeams are assumed to be constant.
 |
| Fig. 5 Variation of natural frequencies of nanobeams under thermal effects for different aspect ratios (KP = KW = 0 and m = 1) . |
It is revealed from Fig. 5 that the natural frequencies of nanobeams increase slightly due to the increase in the temperature changes. However,increasing the aspect ratios leads to the decrease in the natural frequencies. Furthermore,the natural frequencies will increase due to the impact of surface effects because of considering the effective flexural rigidity and surface elastic modulus. Thus,it is concluded that increasing the diameter in thermal environment may change the behavior of nanobeam and its natural frequencies.
In Fig. 6,the effect of large diameters in the presence of surface effects on circular nanobeams is illustrated.
 |
| Fig. 6 Variation of natural frequencies with temperature change in case of large diameters in ab- sence/presence of surface effects (KP = KW = 0 and m = 1) . |
Figure 6 shows that increasing the diameter can lead to the decrease in the natural fre- quency of circular nanobeams significantly. With the increase in the thermal effects,all curves will increase smoothly. In fact,the natural frequencies are little sensitive to temperature vari- ation over the range of 20 ◦C-100 ◦C. In addition,the natural frequencies will decrease when increasing the aspect ratios. As can be shown,the natural frequencies in the presence of sur- face effects are slightly higher as compared with the classical model. It would be pointed out that for increasing aspect ratios,the curves approach each other and the surface effect reduces considerably
Finally,the effect of rotary inertia (m2 6= 0) on natural frequencies is investigated in the presence of surface effects. The values of m = 1 and m = 2 are taken for vibration mode numbers,and the effect of rotary inertia,m2,is discussed in Fig. 7.
 |
| Fig. 7 Effect of rotary inertia on natural frequency of nanobeams with different aspect ratios and mode numbers (KP = KW = N = 0) . |
It is concluded from Fig. 7 that the rotary inertia effect can lead to the increase in the natural frequencies as compared with previous results. In addition,the increase in the mode numbers can lead to the increase in the frequencies for both classical and surface effect cases. Moreover, when increasing the aspect ratios,in the presence of surface effects,the natural frequencies will decrease.
5 ConclusionsA general procedure is developed to review the surface and thermal effects on free vibration of alumina nanobeams resting on a two-parameter elastic foundation. This problem has been modeled within the framework of refined Timoshenko beam theory that considers the impact of surface and thermal effects. The nanobeam is exposed to uniform thermal environment,and the separation of variable approach is employed to discretize the governing equations which are then solved by an analytical method to obtain the natural frequencies of alumina nanobeams with simply-supported boundary conditions. It is concluded that some parameters such as the rotary inertia,the aspect ratio,the Pasternak foundation,and the surface effect can play an important role in natural frequencies of alumina nanobeams. However,the Winkler medium and temperature variation (over the range of 20 ◦C-100 ◦C),do not have any significant impact on the natural frequency of alumina nanobeams. The main conclusions that can be drawn from this investigation are as follows.
(i) For an embedded nanobeam which is exposed to surface and thermal effects,the natural frequencies are always higher than the classical Timoshenko beam model. (ii) When the effect of thermal field is taken into account,the natural frequencies will increase by increasing the temperature. However,it is noted that this effect is negligible for temperature changes in the range of 20 ◦C-100 ◦C.(iii) By increasing the diameter of nanobeams,the natural frequencies decrease as a result of varying the parameters such as the effective flexural rigidity,the residual surface stresses, and the surface parameter (H).
(iv) In the presence of surface effects,by increasing the rotary inertia effect and vibration mode numbers,the natural frequencies may increase.
(v) In the presence of surface effects,the Pasternak foundation may have more impact on increasing the natural frequencies as compared with the Winkler medium.
(vi) The results of the present model are compared with the literature and found to be in good agreement. The results show that the present model can capture correctly the surface effects on the thermal vibration of nanobeams.
| [1] | Wu, G., Hi, H., Hansen, K., Thundat, T., Datar, R., Cote, R., Hagan, M. F., Chakraborty, A. K., and Majumdar, A. Origin of nanomechanical cantilever motion generated from biomolecular interactions. Proc. Natl. Acad. Sci. USA, 98(4), 1560-1564 (2001) |
| [2] | Cui, Y., Zhong, Z. H., Wang, D. L., Wang, W. U., and Lieber, C. M. High performance silicon nanowire field effect transistors. Nano Letters, 3, 149-152 (2003) |
| [3] | Gheshlaghi, B. and Hasheminejad, S. M. Surface effects on nonlinear free vibration of nanobeams. Composites: Part B, 42(4), 934-937 (2011) |
| [4] | Gurtin, M. E. and Murdoch, A. I. A continuum theory of elastic material surfaces. Archive for Rational Mechanics and Analysis, 57(4), 291-323 (1975) |
| [5] | Gurtin, M. E., Weissmuller, J., and Larche, F. A general theory of curved deformable interfaces in solid at equilibrium. Philos. Mag. A, 78(5), 1093-1099 (1998) |
| [6] | Miller, R. E. and Shenoy, V. B. Size dependent elastic properties of nanosized structural elements. Nanotechnology, 11(3), 139-147 (2000) |
| [7] | Ru, C. Q. Simple geometrical explanation of Gurtin-Murdoch model of surface elasticity with clarification of its related versions. Science China, 53(3), 536-544 (2010) |
| [8] | Chen, C. Q., Shi, Y., Zhang, Y. S., Zhu, J., and Yan, Y. J. Size dependence of Young's modulus in ZnO wires. Physical Review Letters, 96(7), 1-4 (2006) |
| [9] | Cuenot, C., Fretigny, C., Demoustier-Champagne, S., and Nysten, B. Surface tension effect on the mechanical properties of nanomaterials measured by atomic force microscopy. Physical Review B, 69(16), 165410 (2004) |
| [10] | Wang, Z. Q., Zhao, Y. P., and Huang, Z. P. The effects of surface tension on the elastic properties of nanostructures. International Journal of Engineering Science, 48, 140-150 (2010) |
| [11] | Wang, L. Vibration analysis of fluid-conveying nanotubes with consideration of surface effects. Physica E, 43(1), 437-439 (2010) |
| [12] | Assadi, A. and Farshi, B. Size dependent stability analysis of circular ultrathin films in elastic medium with consideration of surface energies. Physica E, 43(5), 1111-1117 (2011) |
| [13] | Zang, J. L. and Zhao, Y. P. A diffusion and curvature dependent surface elastic model with application to stress analysis of anode in lithium ion battery. International Journal of Engineering Science, 61, 156-170 (2012) |
| [14] | Karabalin, R. B., Cross, M., and Roukes, M. L. Nonlinear dynamics and chaos in two coupled nanomechanical resonators. Physical Review B, 79, 165309 (2009) |
| [15] | Wang, Z. Q. and Zhao, Y. P. Thermo-hyperelastic models for nanostructured materials. Science China: Physics, Mechanics & Astronomy, 54(5), 948-956 (2011) |
| [16] | Wang, D. H. and Wang, G. F. Surface effects on the vibration and buckling of double-nanobeam- systems. Journal of Nanomaterials, 10, 518706 (2011) |
| [17] | Wang, C. M., Zhang, Y. Y., Ramesh, S. S., and Kitipornchai, S. Buckling analysis of micro- and nano rods/tubes based on nonlocal Timoshenko beam theory. Journal of Physics D: Applied Physics, 39(17), 3904-3909 (2006) |
| [18] | Zhang, Y. Y., Wang, C. M., and Tan, V. B. C. Buckling of multiwalled carbon nanotubes using Timoshenko beam theory. Journal of Engineering Mechanics, 132(9), 952-958 (2006) |
| [19] | Hsu, J. C., Lee, H. L., and Chang, W. J. Flexural vibration frequency of atomic force microscope cantilevers using Timoshenko beam theory. Nanotechnology, 18(28), 285503 (2007) |
| [20] | Abbasi, M., Sabbaghian, M., and Eslami, M. R. Exact closed-form solution of the dynamic cou- pled thermoelastic response of a functionally graded Timoshenko beam. Journal of Mechanics of Materials and Structures, 5(1), 79-94 (2010) |
| [21] | Wang, G. F. and Feng, X. Q. Timoshenko beam model for buckling and vibration of nanowires with surface effects. Journal of Physics D: Applied Physics, 42(15), 155411 (2009) |
| [22] | Lu, C. F., Lim, C., and Yao, W. A. A new analytic sympletic elasticity approach for beams resting on Pasternak elastic foundation. Journal of Mechanics of Materials and Structures, 4(10), 1741-1754 (2009) |
| [23] | Zhu, H. X., Wang, J. X., and Karihaloo, B. Effects of surface and initial stresses on the bending stiffness of trilayer plates and nanofilms. Journal of Mechanics of Materials and Structures, 4(3), 589-604 (2009) |
| [24] | Liu, C., Ke, L. L., Wang, Y. S., Yang, J., and Kitipornchai, S. Thermo-electro-mechanical vibra- tion of piezoelectric nanoplates based on the nonlocal theory. Composite Structure, 106, 167-174 (2013) |
| [25] | Shariyat, M. Dynamic buckling of imperfect laminated plates with piezoelectric sensors and actu- ators subjected to thermo-electro-mechanical loadings, considering the temperature-dependency of the material properties. Composite Structure, 88, 228-239 (2009) |
| [26] | Komijani, M., Kiani, Y., Esfahani, S. E., and Eslami, M. R. Vibration of thermo-electrically post- buckled rectangular functionally graded piezoelectric beams. Composite Structure, 98, 143-152 (2013) |
| [27] | Gibbs, J. W. Thermodynamics, 1st ed., Longmans and Green, New York (1993) |
| [28] | Cammarata, R. C. Surface and interface stress effects in thin films. Progress in Surface Science, 46(1), 1-38 (1994) |
| [29] | Hutchinson, J. R. Shear coefficients of Timoshenko beam theory. Journal of Applied Mechanics, 68(1), 87-92 (2001) |
| [30] | Wang, G. F. and Feng, X. Q. Effects of surface elasticity and residual surface tension on the natural frequency of microbeams. Applied Physics Letters, 90(23), 2319041 (2007) |
| [31] | Martinovic, M., Vlahovic, M., Majstorovic, J., Matovic, M., and Husovic, T. V. Thermal and mechanical properties of high alumina low cement castable. Association of Metallurgical Engineers of Serbia, 18(1), 53-65 (2012) |
| [32] | Jayaseelan, D. D., Ueno, S., Ohji, T., and Kanzaki, S. Thermo-mechanical stability of porous alumina: effect of sintering parameter. Science and Technology of Advanced Materials, 5, 387-392 (2004) |
| [33] | Reddy, J. N. Energy Principles and Variational Methods in Applied Mechanics, John Wiley, New York (2002) |
 2014, Vol. 35
2014, Vol. 35





























