Shanghai University
Article Information
- M. M. RASHIDI, A. HOSSEINI, I. POP, S. KUMAR, N. FREIDOONIMEHR. 2014.
- Comparative numerical study of single and two-phase models of nanofluid heat transfer in wavy channel
- Appl. Math. Mech. -Engl. Ed., 35(7): 831-848
- http://dx.doi.org/10.1007/s10483-014-1839-9
Article History
- Received 2013-6-16;
- in final form 2013-11-15
2. Department of Mathematics, BabeçBolyai University, Cluj-Napoca 400084, Romania;
3. Department of Mathematics, National Institute of Technology, Jamshedpur 831014, Jharkhand, India;
4. Young Researchers & Elite Club, Hamedan Branch, Islamic Azad University, Hamedan 65181-15743, Iran
Since heat exchanger is one of the most used devices in engineering applications,increasing the thermal efficiency is very important. It is found that using the wavy walls can dramatically lead to better heat transfer performance of industrial transport processing. The problem of the flow in a wavy channel was first investigated by Burns and Parks[1]. They used Fourier series under the assumption of Stokes flow for stream function. Flow and heat transfer of convectional fluid in a corrugated wall channel have been studied numerically and experimentally in many works. Asako and Faghri[2] demonstrated that the heat transfer of the sinusoidal channel could be 40% larger than that of the flat plates channel under similar conditions. Rush et al.[3] experimentally studied the heat transfer performance in a sinusoidal wavy channel. Their results showed that the Reynolds number as well as the channel geometry has a direct effect on the local Nusselt number. Wang et al.[4] performed a study about finding correlation for wavy fin- and-tube heat exchangers. They examined the effect of variation of some of the heat exchanger geometric parameters. Wang and Chen[5] numerically investigated laminar forced convection flow and heat transfer for a sinusoidally channel. Their study considered the effects of the wavy geometry,the Reynolds number,and the Prandtl number on the skin friction and the Nusselt number. Fabbri[6] studied the heat transfer in a channel composed of smooth and corrugated wall under laminar flow conditions,and the heat transfer performance of the wavy channel was compared with that of the smooth wall duct. The flow and heat transfer characteristics in a three-dimensional wavy channel were studied numerically by Comini et al.[7]. Nilpueng and Wongwises[8] performed an experimental study of flow pattern and pressure drop of upward liquid single phase flow and air-water two-phase in a sinusoidal wavy channel. Chang et al.[9] investigated the Nusselt number,the pressure drop coefficient,and the thermal performance factors for two furrowed rectangular channels with transverse and skewed sinusoidal wavy walls. Assato and de Lemos[10] numerically investigated the performance of linear and nonlinear eddy viscosity models in a sinusoidal wavy channel under turbulent flow. Stone and Vanka[11] studied the heat transfer in forced convection of wavy channel consisting 14 waves. They performed time dependent simulations for several Reynolds numbers. Their results showed that at low Reynolds numbers,the flow is steady in the complete channel,while as the Reynolds number increases,the flow becomes unsteady.
Low thermal conductivity of conventional base fluids such as water,air,eTc.,has caused researchers to consider nanotechnology to enhance the performance of heat exchangers. Con- vective heat transfer can be improved by addition of metal or metal/oxide solid particles to base fluids. Choi[12] probably was the first person who called nanofluid. Maxwell[13, 14] has focused on enhanced thermal conductivity of nanofluids and has observed that thermal conductivity ofnanofluid mixture improves with the increase in the volume fraction of nanoparticles. Lee et al.[15] determined the thermal conductivity of water and ethylene glycol containing alumina and copper oxide nanoparticles. Their experimental results demonstrated that the thermal conduc- tivity of ethylene glycol based nanofluid was always higher than that of water base nanofluids. Masuda et al.[16] observed almost 30% increase in the thermal conductivity of nanofluid in comparison with base fluid. Some other researchers have attempted to determine the thermal conductivity of nanofluids[17, 18, 19, 20]. Williams et al.[21] found that Al3O3 and ZrO2 nanoparticles in water can increase the heat transfer coefficient under turbulent flow. Xuan and Li[22] ex- perimentally showed flow and heat transfer performance for CuO-water nanofluid in a straight tube under constant heat flux at the wall. Their results demonstrated the enhancement of heat transfer up to 35% nanofluid under turbulent flow. Heris et al.[23, 24] experimentally investigated the convective heat transfer of nanofluid in annular tube under a constant wall temperature boundary condition. The obtained results showed that the heat transfer and Peclet number increase by addition of nanoparticles to base fluid. Forced convection flow of nanofluid in a double tube heat exchanger has been studied by Demir et al.[25]. They presented the effect of the volume fraction of nanoparticles and the Reynolds number on flow and heat transfer characteristics. Ahmed et al.[26] numerically studied the heat transfer and pressure drop char- acteristics of copper-water nanofluid flow isothermally heated corrugated channel. The effect of copper-water nanofluid through two isothermally heated parallel plates under laminar flow has been studied by Santra et al.[27]. Their study has been conducted considering the fluid as Newtonian as well as non-Newtonian for several Reynolds numbers. They observed that the rate of heat transfer increases with the increase in flow as well as the increase in the solid volume fraction of nanofluid. Heidary and Kermani[28] numerically studied heat transfer and flow field in a wavy channel with nanofluid. The effects of the Reynolds number,the volume fraction of nanoparticles,and the wave amplitude were investigated on the local and average Nusselt num- ber and the skin fraction coefficient. In many lectures,nanofluid was aften assumed to be single phase,while other articles have used the two-phase approach[29, 30]. Akbari et al.[31] compared single phase and two-phase models for mixed convection of nanofluid in a horizontal tube under uniform heat flux. Their results demonstrated that single and two-phase models predict almost identical hydrodynamic fields,while these models are very different in thermal fields. Compar- ing the single phase and two-phase models (mixture and Eulerian) for the forced convection in a horizontal tube was presented by Lotfi et al.[32]. They observed that the single phase model and the two-phase Eulerian model underestimate the Nusselt number. Boungiorno[33] was the first one who investigated physical phenomena in the heat transfer of nanofluid. He showed seven slip mechanisms that occur between nanoparticles and base fluid that are inertia,Brownian diffusion,thermophoresis,diffusiophoresis,magnus effect,fluid drainage,and acceleration of gravity. Nanofluid can be also applied in several engineering problems for different conditions and geometries. Rashidi et al.[34] studied the second law of thermodynamics analysis applied to a magnehydrodynamic (MHD) incompressible nanofluid flowing over a porous rotating disk. Rashidi and Erfani[35] investigated the nano boundary-layer flows over streTching surfaces with Navier boundary condition analytically using the differential transform method (DTM)-Pad´e technique that is a combination of the DTM and the Pad´e approximation. Some researchers worked on applications of other analytical methods for simulations of nanofluid flows[36].
The present paper presents the first systematic comparison of computational fluid dynamics (CFD) prediction of forced convection of copper-water nanofluid by the single phase and three different two-phase models (volume of fluid (VOF),mixture,and Eulerian) in the wavy channel. Since there is no experimental data in this case (for wavy channel),in order to illustrate the accuracy of the numerical methods,a horizontal tube is simulated under the constant wall temperature condition,in which the two-phase and the single phase models are compared with the experimental results[24]. Also,the Nusselt number predicted by the single phase for the nanofluid flow in the wavy channel is compared with the published numerical data[28],and thefully developed length for base fluid is simulated and compared with the published data[27, 37]. 2 Model description and numerical method
Forced convection of nanofluid consisting of copper-water in a wavy channel with the opening height 2H and the length L (L=200H) is considered (see Fig. 1). The width of the duct is very large compared to the height. The wavy wall has a constant temperature Tw,and the input nanofluid temperature is Tc (Tc < Tw).
 |
| Fig. 1 Problem geometry and grid configuration. |
The nanofluid is incompressible,and the flow is laminar. The nanoparticles are assumed to have a uniform shape and size. The wavy wall profile is defined by

Since it is not clear which correlation of nanofluid properties gives valid results,the most difficult problem in the nanofluid simulation is the calculation of thermophysical properties. Khanafer and Vafai[38] presented a critical synthesis of the variants for the thermophysical properties of nanofluids. The physical property of pure fluid (water) and nanoparticles (copper) are given in Table 1. In this paper,the following equations are determined for Cu-water nanofluid thermophysical properties.
The effective density can be calculated as follows[39]:
The effective specific heat can be determined as follows[37]:
The effective viscosity can be evaluated by the Magia method[40],
The effective thermal conductivity can be computed as follows[41]:
The governing equations for a steady flow are
2.2 Two-phase models 2.2.1 VOFThe VOF model can model immiscible fluid by solving a single set of momentum equations for all the phase and tracking the volume fraction all over domain by solving a continuity equation for secondary phases. The total summation of the volume fractions is equal to unity. The mass conservation is calculated as
It is known that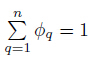 and all properties are determined like
and all properties are determined like
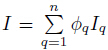 . In the VOF
method,the conservation of momentum and energy equations are Eqs. (6) and (7).
2.2.2 Mixture
. In the VOF
method,the conservation of momentum and energy equations are Eqs. (6) and (7).
2.2.2 Mixture
The mixture model can solve the momentum,continuity,and energy equations for the mixture and the volume fraction equation for the secondary phases. This model uses some correlation to determine the relative velocity between phases.
The conservation of mass is
The conservation of momentum is
where Here,Vdr,k is the drift velocity for secondary phase and defined asThe conservation of energy is
The volume fraction is defined as
where the velocity of a secondary phase is Vp,and the velocity of primary phase is Vf ,so that The drift velocity is given as The relative velocity Vpf proposed by Manninen et al.[42] is determined from while the drag function fdrag proposed by Schiller and Naumann[43] is calculated as where
The Eulerian model is one of the most complex two-phase models that there are various coupling between phases. In this method,separated momentum,continuity,and energy equa- tions are used for different phases while the pressure is shared by all the phases. The volume of each phase is determined by integrating its volume fraction through the domain.
The conservation of mass is
where
The conservation of momentum (qth phase) is
Here,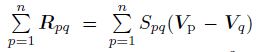 measures the interaction forces between phases Spq =
measures the interaction forces between phases Spq =
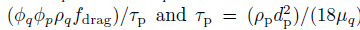 ,
where fdrag indicates the drag friction,which is
determined according to Schiller and Naumann[43] given by (18). The lift force is calculated
from Drew and Lahey[44] equation as
The conservation of energy is
where
,
where fdrag indicates the drag friction,which is
determined according to Schiller and Naumann[43] given by (18). The lift force is calculated
from Drew and Lahey[44] equation as
The conservation of energy is
where


The set of nonlinear equations (mass,momentum,and energy) has been discretized by a control volume approach. The semi implicit method for pressure linked equations (SIMPLE) was used for pressure and velocity coupling[46]. In order to check the accuracy of the results, grid independency tests are done separately for each of four models. Many combinations of node number in the X-direction (240,330,460,740) and in the Y -direction (40,50,70,80) are tested. Since the temperature gradient is large near the wall,the grid is finer close to the wall in all the cases. Figure 2 shows the heat transfer coefficient for four combinations of nod number. It can be seen that changing the grid number in both directions does not affect the results.
 |
| Fig. 2 Grid independency test. |
Since there is no accessible experimental results or two-phase models data in the wavy chan- nel configuration,the validity and the accuracy of the applied numerical method are investigated through simulating the horizontal tube with the constant wall temperature,where experimen- tal results are available[24]. Figure 3 depicts the CFD predictions of nanofluid average heat
 |
| Fig. 3 Average convective heat transfer coefficient in horizontal tube. |
 |
| Fig. 4 Comparison of Nusselt number for nanofluid in wavy channel. |
In order to compare the predictions of the single phase and two phase models,forced convec- tion of Cu-water nanofluid in a wavy channel is investigated. Figure 5 depicts the average heat transfer coefficient in the wavy channel for various Reynolds numbers. The results show the average heat transfer coefficients by two predictions,which are significantly larger than that of the single phase. In the single phase model,we have only a virtual fluid with different physical properties,but two-phase models include the interaction between different phases. If the irreg- ular motion of the particles (Browning motion) increases,this interaction will be raised up and the effect of including the interaction in simulation will be more obvious. In the wavy channel, the Browning motion of the particles will increase due to the effect of distributions that the wavy walls induce in the flow. Also,in the wavy channel,some vortexes have been appearing that amplifies the Browning motion. Therefore,the effect of including the interaction will be greater. We can conclude that such a great difference between two-phase and single phase models in the wavy channel is due to more irregular motion of the nanoparticles. In this study, the heat transfer coefficient prediction by the single phase is lower than that of the two-phase model,while the single phase results are in good agreement with other literatures,although they only considered the single phase (see Fig. 4). Considering two-phase models,the low pre- diction of heat transfer coefficient by the single phase model is reported in Refs. [30, 31, 47, 48]. The Eulerian model has underestimated the heat transfer coefficient among the other two phase models. Lotfi et al.[32] obtained the similar results about the Eulerian model in a horizontal tube.
 |
| Fig. 5 Average of heat transfer coefficient in wavy channel (φ=0.1). |
Figure 6 demonstrates the changes of convective heat transfer coefficient with the increase in the Reynolds number along the wavy wall. Table 3 shows the numerical value of the average heat transfer coefficient of single phase and three different two-phase models with different Reynolds numbers (only along the wavy wall). It is obvious that the average heat transfer coefficient predicted by the single phase model is higher than the two-phase model prediction. In other words,the single phase model is more sensitive to the increase in the velocity than two-phase models.
 |
| Fig. 6 Heat transfer coefficient (φ=0.1). |
Figure 7 shows the heat transfer coefficient predicted by the single phase and three different two-phase models during the wavy wall. It is found that the heat transfer coefficient increases as
 |
| Fig. 7 Heat transfer coefficient (φ=0.1). |
The variations of the skin friction coefficient along the wavy wall are shown in Fig. 8. It is seen that the predictions of different two-phase models are smaller than the single phase model. The VOF model prediction has more volatility compared with two other phase models,while the mixture and Eulerian models are almost the same. All models show that the skin friction coefficient increases when the Reynolds number increases.
 |
| Fig. 8 Skin friction coefficient (φ=0.1). |
Figure 9 shows the changes of heat transfor coefficient along the wavy channel for low Reynolds numbers in two-phase models. Fig. 10Fig. 11Fig. 12Fig. 13 depict variation of heat transfer coeffi- cient along the wavy wall for different values of the volume fraction of nanoparticles. It is seen that at the beginning of the wavy channel,the heat transfer coefficient increases by increasing volume fractions in all models for all Reynolds numbers. Just for two-phase models and low Reynolds numbers,when the volume fraction of nanoparticles increases,the heat transfer co- efficient is enhanced in the front and the middle of the wavy channel,but gradually decreases along the wavy channel (Figs. 11(a),12(a),and 13(a)). For example,at the beginning of the wavy channel,the heat transfer coefficient for 3 percent of volume fraction is greater than the 2 percent one; while at the end of the wavy channel,the heat transfer coefficient in 3 percent of volume fraction is lower than the 2 percent one,as illustrated schematically in Fig. 9. This trend is also observed in the horizontal tube which is shown in Fig. 14. In fact,Fig. 14 is a con- firmation for changing trends of Figs. 10-13,i.e.,changing trends for all the two-phase models are the same.
 |
| Fig. 9 Schematically changes of heat transfer coefficient along wavy channel in low Reynolds numbers in two-phase models. |
 |
| Fig. 10 Effect of nanoparticles on heat transfer coefficient for single phase. |
 |
| Fig. 11 Effect of nanoparticles on heat transfer coefficient for mixture model. |
 |
| Fig. 12 Effect of nanoparticles on heat transfer coefficient for VOF model. |
 |
| Fig. 13 Effect of nanoparticles on heat transfer coefficient for Eulerian model. |
 |
| Fig. 14 Trend of heat transfer coefficient in horizontal tube and effect of volume fraction for twophase models. |
Fig. 15 and Fig. 16 show the velocity and temperature distributions along the wavy channel for a given Reynolds number and a volume fraction. As shown in Fig. 15,the velocity contours predicted by the single phase and two-phase models are different. Also,there is a vortex that is formed within the cavity portion of the wavy,as seen in the enlarge part. In Fig. 16,the temperature contours predicted by two-phase models are essentially the same,but contrary to the results showed in Fig. 15,the differences from the temperature contour predicted by the single phase are important. For example,the temperature distribution at the center of the duct in the single phase model is not well simulated,while the predictions of all the two-phase models depict the isotherm contours at the center of the wavy channel well. The similar conclusions about the velocity and temperature profiles in a horizontal tube were reported by Akbari et al.[31].
 |
| Fig. 15 Velocity contours at wavy channel (Re=250 and φ=0.1). |
 |
| Fig. 16 Temperature contours at wavy channel (Re=250 and φ=0.1). |
The laminar forced convection flow and heat transfer of Cu-water nanofluid for a wavy channel are investigated numerically. The single phase and three different two-phase models predictions (Eulerian,mixture,and VOF) are studied,and their results are compared. The two-phase models are more realistic than the single phase model for simulation of nanofluid. Two-phase models consider the interaction between phases,while in the single phase model,we have only a virtual fluid with different physical properties. The numerical results are validated against published articles data,in order to evaluate the accuracy of this study. The highlights of this investigation are listed below:
(i) The heat transfer coefficient predicted by two-phase models is larger than that of the single phase prediction.
(ii) In this case,the Eulerian model has underestimated the heat transfer coefficient among the other two-phase models.
(iii) The difference between the single and two-phase models predictions is significant in the temperature field,while there is little difference in the hydrodynamic field.
(iv) The friction coefficient predicted by the single phase is larger than that of the two-phase models.
(v) The heat transfer coefficient predicted by the single phase increases with the increase in the volume fraction of nanoparticles for all Reynolds numbers,while for two-phase models and low Reynolds numbers,when increasing the volume fraction of nanoparticles,the heat transfer coefficient enhances in the front and the middle of the wavy channel,but gradually decreases along the wavy channel.
Acknowledgments The authors are very grateful to the anonymous referees for carefully reading the paper and for their constructive comments and suggestions which have improved the paper.
| [1] | Burns, J. C. and Parks, T. A review of steam soak operations in California. Journal of Fluid Mechanics, 29, 405-416 (1967) |
| [2] | Asako, Y. and Faghri, M. Finite volume solutions for laminar flow an heat transfer in a corrugated duct. Journal of Heat Transfer, 109, 627-634 (1987) |
| [3] | Rush, T. A., Newell, T. A., and Jacobi, A. M. An experimental study of flow and heat transfer in sinusoidal wavy passages. International Journal of Heat and Mass Transfer, 42, 1541-1553 (1999) |
| [4] | Wang, C. C., Jang, J. Y., and Chiou, N. F. A heat transfer and friction correlation for wavy fin-and-tube heat exchangers. International Journal of Heat and Mass Transfer, 42, 1919-1924 (1999) |
| [5] | Wang, C. C. and Chen, C. K. Forced convection in a wavy-wall channel. International Journal of Heat and Mass Transfer, 45, 2587-2595 (2002) |
| [6] | Fabbri, G. Heat transfer optimization in corrugated wall channels. International Journal of Heat and Mass Transfer, 43, 4299-4310 (2000) |
| [7] | Comini, G., Nonino, C., and Savino, S. Effect of aspect ratio on convection enhancement in wavy channels. Numerical Heat Transfer, Part A, 44, 21-37 (2003) |
| [8] | Nilpueng, K. and Wongwises, S. Flow pattern and pressure drop of vertical upward gas-liquid flow in sinusoidal wavy channels. Experimental Thermal and Fluid Science, 30, 523-534 (2006) |
| [9] | Chang, S. W., William Lees, A., and Chou, T. Heat transfer and pressure drop in furrowed channels with transverse and skewed sinusoidal wavy walls. International Journal of Heat and Mass Transfer, 52, 4592-4603 (2009) |
| [10] | Assato, M. and de Lemos, M. J. S. Turbulent flow in wavy channels simulated with nonlinear models and a new implicit formulation. Numerical Heat Transfer, Part A, 56, 301-324 (2009) |
| [11] | Stone, K. and Vanka, S. P. Numerical study of developing flow and heat transfer in a wavy passage. Journal of Fluids Engineering, 121, 713-719 (1999) |
| [12] | Choi, U. S. Enhancing thermal conductivity of fluids with nanoparticles. ASME FED, 231, 99-103 (1995) |
| [13] | Maxwell, J. C. A Treatise on Electricity and Magnetism, 2nd ed., Cambridge Oxford University Press, Oxford (1904) |
| [14] | Maxwell, J. C. Electricity and Magnetism, Clarendon Press, Oxford (1873) |
| [15] | Lee, S., Choi, S. U. S., Li, S., and Eastman, J. A. Measuring thermal conductivity of fluids containing oxide nanoparticles. Journal of Heat Transfer, 121, 280-289 (1999) |
| [16] | Masuda, H., Ebata, A., Teramae, K., and Hishinuma, N. Alteration of thermal conductivity and viscosity of liquid by dispersing ultra-fine particles (dispersions of鈥擜l2O3, SiO2, and TiO2 ultrafine particles) (in Japanese). Netsu Bussei, 4, 227-233 (1993) |
| [17] | Eastman, J. A., Choi, S. U. S., Li, S., Yu, W., and Thompson, L. J. Anomalously increase effective thermal conductivities of ethylene glycol-based nanofluids containing copper nanoparticles. Applied Physics Letters, 78(6), 718-720 (2001) |
| [18] | Xuan, Y. and Li, Q. Heat transfer enhancement of nanofluids. International Journal of Heat and Fluid Flow, 21, 58-64 (2000) |
| [19] | Pak, B. C. and Cho, Y. I. Hydrodynamic and heat transfer study of dispersed fluids with submicron metallic oxide particles. Experimental Heat Transfer, 11(2), 151-170 (1998) |
| [20] | Wang, X., Xu, X., and Choi, S. U. S. Thermal conductivity of nanoparticles-fluid mixture. Journal of Thermophysics and Heat Transfer, 13(4), 474-480 (1999) |
| [21] | Williams, W., Buongiorno, J., and Hu, L. W. Experimental investigation of turbulent convective heat transfer and pressure loss of alumina/water and zirconia/water nanoparticle colloids (nanofluids) in horizontal tubes. ASME Journal of Heat Transfer, 130(1), 42412-42419 (2008) |
| [22] | Xuan, Y. and Li, Q. Investigation on convective heat transfer and flow features of nanofluids. Journal of Heat Transfer, 125(1), 151-155 (2003) |
| [23] | Heris, S. Z., Etemad, S. G., and Esfahany, M. N. Experimental investigation of Oxide nanofluids laminar flow convective heat transfer. International Communications in Heat and Mass Transfer, 33, 529-535 (2006) |
| [24] | Heris, S. Z., Esfahany, M. N., and Etemad, S. G. Experimental investigation of convective heat transfer of Al2O3/water nanofluid in circular tube. International Journal of Heat and Fluid Flow, 28, 203-210 (2007) |
| [25] | Demir, H., Dalkilic, A. S., Kürekci, N. A., Duangthongsuk, W., and Wongwise, S. Numerical investigation on the single phase forced convection heat transfer characteristics of TiO2 nanofluids in a doubletube counter flow heat exchanger. International Communications in Heat and Mass Transfer, 38, 218-228 (2011) |
| [26] | Ahmed, M. A., Shuaib, N. H., Yusoff, M. Z., and Al-Falahi, A. H. Numerical investigations of flow and heat transfer enhancement in a corrugated channel using nanofluid. International Communications in Heat and Mass Transfer, 38, 1368-1375 (2011) |
| [27] | Santra, A. K., Sen, S., and Chakraborty, N. Study of heat transfer due to laminar flow of copperwater nanofluid through two isothermally heated parallel plates. International Journal of Thermal Science, 48, 391-400 (2009) |
| [28] | Heidary, H. and Kermani, M. J. Effect of nano-particles on forced convection in sinusoidal-wall channel. International Communications in Heat and Mass Transfer, 37, 1520-1527 (2010) |
| [29] | Mirmasoumi, S. and Behzadmehr, A. Numerical study of laminar mixed convection of a nanofluid in a horizontal tube using two-phase mixture model. Applied Thermal Engineering, 28, 717-727 (2008) |
| [30] | Behzadmehr, A., Avval, M. S., and Galanis, N. Prediction of turbulent forced convection of a nanofluid in a tube with uniform heat flux using a two phase approach. International Journal of Heat and Fluid Flow, 28, 211-219 (2007) |
| [31] | Akbari, M., Galanis, N., and Behzadmehr, A. Comparative analysis of single and two-phase models for CFD studies of nanofluid. International Journal of Thermal Sciences and Heat Transfer, 50, 1343-1354 (2011) |
| [32] | Lotfi, R., Saboohi, Y., and Rashidi, A. M. Numerical study of forced convective heat transfer of nanofluids: comparison of different approaches. International Communications in Heat and Mass Transfer, 37, 74-78 (2010) |
| [33] | Buongiorno, J. Convective transport in nanofluid. Journal of Heat Transfer, 128, 240-250 (2006) |
| [34] | Rashidi, M. M., Abelman, S., and Freidoonimehr, N. Entropy generation in steady MHD flow due to a rotating porous disk in a nanofluid. International Journal of Heat and Mass Transfer, 62, 515-525 (2013) |
| [35] | Rashidi, M. M. and Erfani, E. The modified differential transform method for investigating nano boundary-layers over streTching surfaces. International Journal of Numerical Methods for Heat & Fluid Flow, 21, 864-883 (2011) |
| [36] | Rashidi, M. M., Freidoonimehr, N., Hosseini, A., Anwar Bég, O., and Hung, T. K. Homotopy simulation of nanofluid dynamics from a non-linearly streTching isothermal permeable sheet with transpiration. Meccanica, 49, 469-482 (2014) |
| [37] | Durst, F., Ray, S., Unsal, B., and Bayoumi, O. A. The development lengths of laminar pipe and channel flows. ASME Journal of Fluid Engineering, 127, 1154-1160 (2005) |
| [38] | Khanafer, K. and Vafai, K. A critical synthesis of thermophysical characteristics of nanofluids. International Journal of Heat and Mass Transfer, 54, 4410-4428 (2011) |
| [39] | Khanafer, K., Vafai, K., and Lightstone, M. Buoyancy-driven heat transfer enhancement in a two dimensional enclosure utilizing nanofluids. International Journal of Heat and Mass Transfer, 46, 3639-3653 (2003) |
| [40] | Maïgaa, S. B., Palma, S. J., and Nguyena, C. T. Heat transfer enhancement by using nanofluids in forced convection flows. International Journal of Heat and Fluid Flow, 26, 530-546 (2005) |
| [41] | Yu, W. and Choi, S. U. S. The role of interfacial layers in the enhanced thermal of nanofluids: a renovated Maxwell mode. Journal of Nanoparticle Research, 5(1-2), 167-171 (2003) |
| [42] | Manninen, M., Taivassalo, V., and Kallio, S. On the Mixture Model for Multiphase Flow, VTT Publications, Tekniikantie (1996) |
| [43] | Schiller, L. and Naumann, A. A drag coefficient correlation. Zeitschrift Vereines Deutscher Ingenieure, 77, 318-325 (1935) |
| [44] | Drew, D. A. and Lahey, R. T. Particulate Two-phase Flow, Butterworth-Heinemann, Boston (1993) |
| [45] | Ranz, W. E. and Marshall, W. R. Evaporation from drops. Chemical Engineering Progress, 48, 141-146 (1952) |
| [46] | Patankar, S. V. Numerical Heat Transfer and Fluid Flow, Hemisphere Publishing Corporation, Taylor and Francis Group, New York (1990) |
| [47] | Haghshenas Fard, M., Esfahany, M. N., and Talaie, M. R. Numerical study of convective heat transfer of nanofluids in a circular tube two-phase model versus single-phase model. International Communications in Heat and Mass Transfer, 37, 91-97 (2010) |
| [48] | Kalteh, M., Abbassi, A., Saffar-Aval, M., and Harting, J. Eulerian-Eulerian two-phase numerical simulation of nanofluid laminar forced convection in a microchannel. International Journal of Heat and Fluid Flow, 32, 107-116 (2011) |
 2014, Vol. 35
2014, Vol. 35





























