Shanghai University
Article Information
- A. NAYAK, S. PANDA, D. K. PHUKAN. 2014.
- Soret and Dufour effects on mixed convection unsteady MHD boundary layer flow over stretching sheet in porous medium with chemically reactive species
- Appl. Math. Mech. -Engl. Ed., 35(7): 849-862
- http://dx.doi.org/10.1007/s10483-014-1830-9
Article History
- Received 2013-2-6;
- in final form 2014-2-14
2. Department of Mathematics, National Institute of Technology, Calicut 673601, India;
3. Department of Mathematics, Moran College, Moranhat, Assam 785670, India
The analysis of magnetohydrodynamics (MHD) viscous fluid with heat and mass transfer through a porous medium has been a subject of fundamental importance as it is relevant to several industrial applications such as crystal magnetic damping control,hydromagnetic chro- matography,chemical catalytic reactors,heat and mass transfer characteristics in nanofluid for power plants,heat exchange between soil and atmosphere,packed sphere beds,and mi- grations of moisture through the air contained in fibrous insulation. This industrial context has drawn attention of many fluid dynamists and applied mathematicians. The exhaustive volume of work devoted to this area includes the most recent books by Nield and Bejan[1], Ingham and Pop[2],Vafai[3],and Pop and Ingham[4]. The natural convection flow in porous media with combined buoyancy effects due to heat and mass transfer has been studied by many researchers. In such problems,the coupling between transport of heat and mass takes placedue to influence of density variations with temperature and concentration. However,there are circumstances where direct coupling between temperature and concentration is possible when the cross diffusion (Soret and Dufour effects) is not negligibly small. The Soret effect refers to the mass flux produced by temperature gradients,and the Dufour effect refers to the heat flux produced by concentration gradients. The close relationship between these two numbers are demonstrated in Refs. [5] and [6]. Many researchers[7, 8, 9, 10] did not consider Soret and Dufour effects. They assumed insignificant influence of species and temperature cross diffusion terms in comparison to heat and mass diffusion terms. However,in some circumstances,the order of magnitude analysis shows that the cross diffusion terms are very significant as compared to heat and mass diffusion terms. For example,the Soret and Dufour effects play a significant role in the problems concerning in contaminant transport in ground water,exploitation of geothermal reservoirs,etc.
The pioneering work of Tyvand[11] and Patil et al.[12] laid the foundation stone in this field. The problem has been revisited several times since this seminal work with the inclusion of additional physics or more complex rheology. Chamkha et al.[13] examined the cross diffusion effects on the steady problem of a micro-polar fluid over a vertical plate embedded in a porous medium with chemical reaction. Postelnicu[14, 15] studied the two-dimensional stagnation-point flow of a fluid saturated porous medium using the Darcy-Boussinesq model including Soret and Dufour effects. Tsai and Huang[16] extended the standard formulation to Hiemenz flow. Later,the formulation was extended for the viscoelastic fluid[17, 18] and more recently for the Sisko fluid[19]. Osalusi et al.[20] extended Postelnicu’s contribution by analyzing the flow due to rotating disk with viscous dissipation and Ohmic heating,while Affiy[21] studied the MHD flow on a stretching sheet with thermal diffusion and diffusion thermo effects. Anwar et al.[22] focused on the numerical study of MHD heat and mass transfer from a stretching surface placed in a porous medium with Soret and Dufour effects. Sallam[23] analyzed the thermal-diffusion and diffusion-thermo effects on mixed convection heat and mass transfer in a porous medium. The double diffusive natural convective boundary layer flow of a nanofluid past a vertical plate was recently studied by Kuznetsov and Nield[24].
A common feature of the literature cited above is that most of these studies have been conducted on the steady flow. Neglecting Soret and Dufour effects,Rashad and El-Kabeir[9] recently studied the heat and mass transfer in unsteady flow by mixed convection boundary layer over a stretching sheet in a porous configuration. Keeping in view the importance of double diffusive systems which arise in a variety of geological system and industrial processes, the present paper investigates the Soret and Dufour effects in a transient mixed convection boundary layer flow,where heat and mass transfer in a porous medium over a stretching sheet.
The outline of the paper is as follows. In the next section,we describe the model for the unsteady two-dimensional laminar heat and mass transfer flow of incompressible MHD fluid in a porous medium over an impermeable vertical heated stretching sheet. The solution procedure of the unsteady problem is explained in Section 3,and the penultimate section reports the simulation results for the different flow parameters and the paper closes with a conclusion.
2 Problem formulationA typical flow scenario is illustrated in Fig. 1. It shows the unsteady two-dimensional laminar heat and mass transfer flow of an incompressible electrically conducting viscous fluid in a porous medium past an impermeable vertical heated stretching sheet in the presence of chemical reaction. The x-axis is taken along the stretching direction of the sheet with the stretching rate Ue(x) = ax,where a > 0,and the y-axis is normal to the surface of the sheet. A magnetic field of uniform strength B0 is applied in the negative direction of the y-axis,and the gravity acts in the negative x-direction. It is assumed that the sheet is non-conducting,and the effects of the radiating and Joule heating,the viscous dissipation,the Hall effects,and induced fieldsare neglected,while the Soret and Dufour effects are examined. Additionally,the physical properties,i.e.,the viscosity,the heat capacity,the thermal diffusivity,and the mass diffusivity of the fluid remain invariant throughout the field. Moreover,the density variation and the effects of the buoyancy are taken into account in the momentum equation (the Boussinesq approximation).
 |
| Fig. 1 Sketch of flow geometry. |
Initially,the sheet and the fluid are at the same temperature T∞ in a stationary condition with concentration level C∞. At time t > 0,fluid starts moving with the stretching rate Ue, and its temperature and concentration at the sheet are raised to Tw and Cw,respectively.
The continuity,momentum,energy,and concentration equations describing the flow under the Boussinesq approximation can be written as[9, 25]
The symbol u and v denote the fluid velocity in the x- and y-directions,respectively. Here, T and C are the temperature and concentration variables,ρ is the density,ν is the kinematic viscosity,α is the thermal diffusivity,De is the mass diffusivity,g is the acceleration due to gravity,βT is the thermal expansion coefficient,βC is the coefficient of volumetric expansion with concentration,K is the permeability of the porous medium,K1 is the chemical reaction rate on the species concentration,Κ is the electrical conductivity,cp is the specific heat at constant temperature,cs is the concentration susceptibility,Tm is the mean fluid temperature, and KT is the thermal diffusion ratio.The initial and boundary conditions of Eqs. (1)-(4) are
852 A. NAYAK,S. PANDA,and D. K. PHUKAN Here,both the wall temperature and concentration are assumed to have linear forms,i.e., where b and c are constants. b > 0 means a heated surface (Tw > T∞),while b < 0 means a cooled surface (Tw < T∞). The similar type of boundary conditions are also used by Zaimi et al.[26] in connection with flow of rotating viscoelastic fluid over a stretching surface and by Rani et al.[27] in a transient flow problem.Following Ishak and Nazar[25] and Rashad and El-Kabeir[9],we look for the solution to Eqs. (1)-(4) of the form
where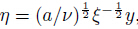 ,and the prime denotes differentiation with respect to η. It can be noted
that Eq. (7) is compatible with Eq. (1),and the definition of ξ indicates that the region of time
integration 0 6 t 6 1 may become finite,i.e.,0 6 ξ 6 1.
,and the prime denotes differentiation with respect to η. It can be noted
that Eq. (7) is compatible with Eq. (1),and the definition of ξ indicates that the region of time
integration 0 6 t 6 1 may become finite,i.e.,0 6 ξ 6 1.
Using Eq. (7) in Eqs. (2)-(4),we get the following dimensionless aligns:
The dimensionless numbers are as follows. The Prandtl number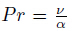 represents the ratio
of momentum to thermal diffusivity. The Schmidt number
represents the ratio
of momentum to thermal diffusivity. The Schmidt number 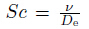 represents the ratio of
momentum to mass diffusivity. The dimensionless number
represents the ratio of
momentum to mass diffusivity. The dimensionless number 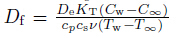 is the Dufour
number,
is the Dufour
number,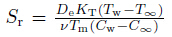 is the Soret number,
is the Soret number,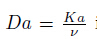 is the Darcy number,
is the Darcy number,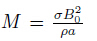 is the local magnetic field parameter,
is the local magnetic field parameter,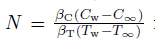 is the ratio of buoyancy force due to
thermal diffusion,
is the ratio of buoyancy force due to
thermal diffusion,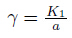 a is the chemical reaction parameter,and
a is the chemical reaction parameter,and 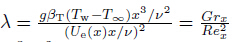 is the mixed convection parameter,where
is the mixed convection parameter,where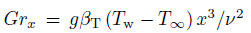 is the local Grashof
number and
is the local Grashof
number and 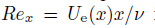 is the local Reynolds number. It may be noted that λ > 0
corresponds to the assisting flow (heated plate),λ < 0 corresponds to the opposing flow (cooled
plate),and λ = 0 corresponds to the forced convection flow,respectively.
is the local Reynolds number. It may be noted that λ > 0
corresponds to the assisting flow (heated plate),λ < 0 corresponds to the opposing flow (cooled
plate),and λ = 0 corresponds to the forced convection flow,respectively.
In view of the scaling relations (7),the corresponding boundary conditions (5) are
It may be recorded that for M = Df = Sr = 0,Eqs. (8)-(10) together with Eq. (11) are the same as those obtained by Rashad and El-Kabeir[9]. However,a small discrepancy is observed in the fourth term of Eq. (10). It is found in the present work that the chemical reaction parameter is multiplied by the non-dimensional time ξ and the chemical reaction variable Φ,and γ has effects in the perturbation analysis. Furthermore,for M = Df = Sr = Da = N = = 0 ,the model equations reduce to those of Ishak and Nazar[25].
The important physical parameters for this flow and the heat and mass transfer situation are the local skin-friction coefficient Cf ,the local Nusselt number Nux,and the Sherwood number Shx. These physical quantities can be defined as
Here,μ is the coefficient of viscosity,k is the thermal conductivity of the fluid,and qw and Jw are the wall heat and the mass flux,respectively. Using non-dimensional relation (7) in Eqs. (12)-(14),we can obtain 3 Numerical solutionThe model (8)-(10) together with boundary conditions (11) are the parabolic partial differ- ential equations. Instead of solving these partial differential equations directly,we look for the particular cases of the problem,which are the system of ordinary differential equations with a set of constraints at the boundary and can be easily solved by the shooting method. The solution procedure for the entire time domain 0 6 ξ 6 1 is explained in the following part.
3.1 Unsteady solution at initial stage ξ = 0When the time scale ξ = 0,i.e.,for an initial unsteady flow,it corresponds to τ = 0, Eqs. (8)-(10) reduce to
subject to the boundary conditionsIt may be noted that for Df = Sr = 0,Eqs. (18) and (19) are the same as those obtained by Rashad and El-Kabeir[9]. However,due to discrepancy in the concentration (10),the effects of chemical reaction term in the concentration equation at the initial unsteady equation is not visible in the present work.
3.2 Solution for steady state when ξ = 1,i.e.,final steady flowFor ξ = 1 which corresponds to τ ! 1,Eqs. (8)-(10) reduce to
subject to the boundary conditions 3.3 Solution for small ξ (or τ)The approximate solutions to (8)-(10) subject to the boundary conditions (11) which are valid for the region ξ 6 1 and equivalent to the small time τ << 1,can be expressed in a regular perturbation with respect to ξ,i.e.,
Plugging Eq. (26) into Eqs. (8)-(10) and collecting equations of different orders,we have the following equations.
Zeroth order:
subject to the boundary conditionsFirst order:
subject to the boundary conditionsSecond order:
subject to the boundary conditionsEquations of the problem at different regimes are the system of ordinary differential equa- tions with corresponding boundary conditions. In order to obtain the solution in the entire time domain 0 6 ξ 6 1,we solve the problem step by step. For the solution of the initial and final state,we solve Eqs. (18)-(21) and (22)-(25),respectively. For the solution in the time domain 0 < ξ < 1,we solve Eqs. (31)-(33) and Eqs. (35)-(37) subject to boundary conditions (34) and (38). The leading order perturbed equations (27)-(29) with boundary condition (30) are the same as the equations of the unsteady solution at the initial state. Upon substitution of the leading,first,and second order solutions in Eq. (26),we obtain the solution in the time regime 0 < ξ < 1.
4 Results and discussionThe numerical solution to the boundary value problem of ordinary differential equations is obtained by the Runge-Kutta method in association with the shooting technique. It may be noted that the source of error in the simulation may come from the prescribed boundary conditions at the infinity. The reason is that the physical domain under consideration is un- bounded whereas the computational domain is finite. In fact,the far field boundary condition usually depends on the physical parameters of the problem,and its value needs to be adjusted as the values of the parameters change. In practice,the computational domain is chosen to be sufficiently large,so that the numerical solution closely approximates the terminal boundary conditions at infinity. Here,the boundary condition at the far end has been fixed to 10 and is suitably less than 10 depending on the choice of the parameters.
4.1 ValidationTo assure the validity and accuracy of the numerical method,the numerical results for the local skin friction coefficient and local Nusselt number at non-dimensional time (ξ = 1) in the absence of the cross diffusion terms,the porosity parameter,and the buoyancy force are compared with those reported by [25] and [9]. The comparison is shown in Table 1 and found in excellent agreement. In order to compute the local skin friction coefficient and the local Nusselt number,the simulation is performed in the computational domain 0 6 η 6 10 with 500 grid points.
 |
It is observed that for the large value of Pr,the computational domain has to be large since the far end boundary condition depends on the choice of Pr. For example,when we perform the simulation in the domain 0 6 η 6 7 for the parameters Pr = 7 and λ = 10 and keep other parameters the same as given in Table 1,we obtain f′′(0)=0.765 3 and −θ′(0)=3.312 3. Similarly for Pr = 7 and λ = 100,it is noted that f′′(0) = 12.632 9 and −θ′(0)=4.253 2,and these makes large differences in the results for f′′(0) and −θ′(0) as compared to those obtained by Refs. [9] and [25] and Table 1.
4.2 Velocity,temperature,and concentration distributionThe influence of various flow parameters on the velocity (f′),the temperature (θ),and the concentration fields (Φ) has been analyzed through graphs . Fig. 2Fig. 3Fig. 4 show the velocity,the temperature,and the concentration profiles,respectively,for various values of non-dimensional time (ξ) with Df = 0.1,Sr = 1,Pr = 0.7,Sc = 0.22,Da = 2,N = 1,λ = 1, = 1,and M = 0.1.
 |
| Fig. 2 Variations of velocity profiles f′ from initial state (ξ=0) to final steady state (ξ = 1). |
 |
| Fig. 3 ariations of temperature profiles θ from initial state (ξ=0) to final steady state (ξ = 1). |
 |
| Fig. 4 Variations of concentration profiles Φ from initial state (ξ = 0) to final steady state (ξ = 1). |
Figure 2 shows the advancement of velocity from the initial state (ξ = 0) to the final steady state (ξ = 1). It is clear that with an increase in ξ,the velocity increases and approachesthe final steady profile corresponding to ξ = 1 and the temperature and concentration profiles decrease (see Fig. 3Fig. 4). Thus,there is a smooth transition from small time solution ξ = 0 to large time solution ξ = 1,and these results are in conformity with the earlier reported results (Rashad and El-Kabeir[9]).
The velocity,the temperature,and the concentration profiles for various values of M with Df = 0.1,Sr = 1,Pr = 0.7,Sc = 0.22,Da = 4,N = 1,λ = 4,and = 1 are plotted in Fig. 5Fig. 6Fig. 7,respectively.
 |
| Fig. 5 Effect of magnetic parameter on veloc- ity profiles f′ under Soret and Dufour effects. |
 |
| Fig. 6 ffect of magnetic parameter on tem- perature profiles θ under Soret and Dufour effects. |
 |
| Fig. 7 Effect of magnetic parameter on con- centration profiles Φ under Soret and Dufour effects. |
Figure 5 displays the effects ofM on the velocity. The increase in the value ofM fromM = 0 (the non-conducting case) to M = 4 (the conducting case) at the final steady state ξ = 1 causes the reduction in velocities across the boundary layer. Physically,the higher value of M implies the higher Lorentz force which has tendency to slow down the motion of the conducting fluid in the boundary layer. The maximum velocity is seen for non-conducting fluid close to the wall at η = 1 and then the velocity decreases with the increase in M and finally approaches the far field boundary condition. The increase in the value of M results in the increase in the temperature (see Fig. 6) due to the fact that the extra work used to drag the fluid against the magnetic field is dissipated in the form of thermal energy in thermal boundary. This results in heating of theboundary layer and consequently the temperature increases in the boundary layer region. The deceleration of flow due to the magnetic force enhances the species diffusion in the layer,and that results in the increase in the concentration (see Fig. 7). Thus,the results indicate that the magnetic parameter is found to have significant effect on the flow fields.
The Dufour effects on the velocity,the temperature,and the concentration are examined in Fig. 8 , Fig. 9,Fig. 10 with Sr = 1,Pr = 0.7,Sc = 0.22,Da = 4,N = 1,λ = 4, = 1,and M = 0.1. It can be seen that the velocity and the temperature increase with the increase in the Dufour number (see Fig. 8 and Fig. 9),while the reverse effect is observed in the case of the concentration profile (see Fig. 10). Physically,the Dufour term that appears in the temperature equation measures the contribution of concentration gradient to thermal energy flux in the flow domain. It has a vital role in enhancing the flow velocity and the ability to increase the thermal energy in the boundary layer. As a result,the temperature profile at all time stages increases with the increase in Df ,while the reverse effect is observed in the case of the concentration profile (see Fig. 10).
 |
| Fig. 8 Effect of Dufour number on velocity profile. |
 |
| Fig. 9 Effect of Dufour number on tempera- ture profile. |
 |
| Fig. 10 Effect of Dufour number on concentration profile. |
The influence of the Soret number on the velocity,the temperature,and the concentration is discussed in Fig. 11Fig. 12Fig. 13 with Df = 1.0,Pr = 0.7,Sc = 0.22,Da = 4,N = 1,λ = 4, = 1,and M = 0.1. It is noted that an increase in the Soret number due to the contribution of temperature gradients to species diffusion increases the concentration (see Fig. 13) and consequently enhances the velocity profile (see Fig. 11). However,the effect of Sr on the temperature profile is quite opposite to that of Df (see Fig. 12).
 |
| Fig. 11 Effect of Soret number on velocity profile. |
 |
| Fig. 12 Effect of Soret number on tempera- ture profile. |
 |
| Fig. 13 Effect of Soret number on concentration profile. |
The typical flow profiles for the velocity,the temperature,and the concentration for various values of the chemical reaction parameter and the non-dimensional time ξ with Pr = 0.7, Sc = 0.22,Df = 0.5,Sr = 0.1,Da = 5,λ = 10,N = 1,and M = 1 are presented in Fig. 14Fig. 15Fig. 16. From these figures,we observe that both the velocity and concentration profiles decrease with the increase in the chemical reaction parameter. This implies that the concentration boundary layer becomes thinner,and at the same time,the concentration diffusion species decrease. However,the reduction in mass diffusion enhances the temperature (see Fig. 15) of the fluid and causes the decrease in the velocity.
 |
| Fig. 14 Effect of chemical reaction parameter on velocity profile. |
 |
| Fig. 15 Effect of chemical reaction parameter on temperature profile. |
 |
| Fig. 16 Effect of chemical reaction parameter on concentration profile. |
The effect of the magnetic parameter (M) in the presence of the Soret and the Dufour num- bers on the skin friction and the Nusselt and Sherwood numbers is analyzed in Fig. 17Fig. 18Fig. 19 the when Pr = 0.7,Sc = 0.22,Da = 2.0,N = 4.0,λ = 10.0,and = 2.0. In Fig. 17,we plot the skin friction versus the non-dimensional time (ξ). From this result,we see that the magnitude of skin friction increases as the Dufour and Sherwood numbers and the time increase. More- over,increasing the magmatic parameter (M) strongly reduces the value of skin friction. In Fig. 18,the Nusselt number is plotted against the time (ξ). This simulation result shows that the value of the Nusselt number is higher for higher values of Sr. Moreover,it decreases up to approximately ξ 6 0.7 and then increases with the increase in Df . It is also interesting to note that when the magnetic parameter increases from M = 0.5 to M = 2 with fixed Df = 1.0 and Sr = 3,there is a slight decrease in the rate of heat transfer. The Sherwood number is visualized against time in Fig. 19. We can see that the increase in the Dufour number causes
 |
| Fig. 17 Effect of magnetic parameter on local skin friction coefficient under Soret and Dufour effects. |
 |
| Fig. 18 ffect of magnetic parameter on lo- cal Nusselt number under Soret and Dufour effects. |
 |
| Fig. 19 Effect of magnetic parameter on local Sherwood number under Soret and Dufour effects. |
This work studied the Soret and Dofour effects on the mixed convection flow in the hydro- magnetic unsteady flow past an impermeable vertical stretching sheet in a fluid-saturated porous medium in the presence of chemical reaction. Numerical solutions are obtained using the Runge-Kutta method in association with the shooting technique for the self-similar form of the incompressible boundary layer unsteady equations for the entire unsteady domain,i.e., from the initial unsteady flow to the final steady flow. The smooth transition of the flow from small time solution to large time solution is observed. It has been further observed that the velocity profile increases with the advancement of time from the initial unsteady state to the final steady state,while the temperature and concentration fields experience reverse effect. It is also found that the inclusion of magnetic parameter on the flow increases the temperature and concentration profiles,while it decreases the velocity field,the magnitude of skin friction coefficient,and the local rate of heat transfer and local rate of mass transfer. Moreover,it is seen that the skin-friction coefficient and the Nusselt number increase with the increase in the Soret (Sr) and Dufour (Df ) numbers,whereas the reverse effect is observed in the case of the Sherwood number for Sr and the same effect for Df in the presence of magnetic field. Another interesting result is that the skin-friction and the Nusselt number are higher in the absence of magnetic field,when the Soret and Dufour numbers are considered,while a reverse effect is observed in the case of the Sherwood number.
| [1] | Nield, D. A. and Bejan, A. Convection in Porous Media, 3rd ed., Springer, New York (2006) |
| [2] | Ingham, D. B. and Pop, I. Transport Phenomena in Porous Media, Vol. III, Pergamon, Oxford (2005) |
| [3] | Vafai, K. Handbook of Porous Media, Taylor and Francis, New York (2005) |
| [4] | Pop, I. and Ingham, D. B. Convective Heat Transfer: Mathematical and Computational Modeling of Viscous Fluids and Porous Media, Pergamon, Oxford (2001) |
| [5] | Knobloch, E. Convection in binary fluids. Physics of Fluids, 23, 1918-1920 (1980) |
| [6] | Taslim M. E. and Narusawa, U. Binary fluid convection and double diffusive convection in a porous medium. Journal of Heat Transfer, 108, 221-224 (1986) |
| [7] | Parida, S. K., Acharya, M., Dash, G., and Panda, S. MHD heat and mass transfer in a rotating system with periodic suction. The Arabian Journal for Science and Engineering, 36, 1139-1151 (2011) |
| [8] | Fan, J. R., Shi, J. M., and Xu, X. Z. Similarity solution of mixed convection with diffusion and chemical reaction over a horizontal moving plate. Acta Mechanica, 126, 59-69 (1998) |
| [9] | Rashad, A. M. and El-Kabeir, S. M. M. Heat and mass transfer in transient flow by mixed convection boundary layer over a stretching sheet embedded in a porous medium with chemically reactive species. Journal of Porous Media, 13(1), 75-85 (2010) |
| [10] | Saha, S. C. and Hossain, M. A. Natural convection flow with combined buoyancy effects due to thermal and mass diffusion in a thermally stratified media. Nonlinear Analysis: Modeling and Control, 9(1), 89-102 (2004) |
| [11] | Tyvand, P. A. Thermohaline instability in anisotropic porous media. Water Resources Research, 16, 325-330 (1980) |
| [12] | Patil, P., Paravathy, C. P., and Venkatakrishnan, K. S. Thermohaline instability in a rotating anisotropic porous medium. Applied Scientific Research, 46, 73-88 (1989) |
| [13] | Chamkha, A. J., Al-Mudhaf, A., and Al-Yatama, J. Double diffusive convective flow of a micro- polar fluid over a vertical plate embedded in a porous medium with a chemical reaction. Interna- tional Journal of Fluid Mechanics Research, 6, 529-551 (2004) 862 A. NAYAK, S. PANDA, and D. K. PHUKAN |
| [14] | Postelnicu, A. Influence of chemical reaction on heat and mass transfer by natural convection from vertical surfaces in porous media considering Soret and Dufour effects. Heat and Mass Transfer, 43, 595-602 (2007) |
| [15] | Postelnicu, A. Heat and mass transfer by natural convection at a stagnation point in a porous medium considering Soret and Dufour effects. Heat and Mass Transfer, 46, 831-840 (2010) |
| [16] | Tsai, R. and Huang, J. S. Heat and mass transfer for Soret and Dufour's effects on Hiemenz flow through porous medium onto a stretching surface. International Journal of Heat and Mass Trasfer, 52, 2399-2406 (2009) |
| [17] | Hayat, T., Mustafa, M., and Pop, I. Heat and mass transfer for Soret and Dufour's effect on mixed convection boundary layer flow over a stretching vertical surface in a porous medium filled with a viscoelastic fluid. Communications in Nonlinear Science and Numerical Simulation, 15, 1183-1196 (2010) |
| [18] | Gbadeyan, J. A., Ogunsola, A. S., Ogunsola, A. W., Agboola, O. O., and Olanrewaju, P. O. Heat and mass transfer for Soret and Dufour's effect on mixed convection boundary layer flow over a stretching vertical surface in a porous medium filled with a viscoelastic fluid in the presence of magnetic field. Global Journal of Science and Frontier Research, 11(8), 96-114 (2011) |
| [19] | Oladapo, O. P. Dufour and Soret effects of a transient free convective flow with radiative heat transfer past a flat plate moving through a binary mixture. The Pacific Journal of Science and Technology, 11(1), 163-172 (2010) |
| [20] | Osalusi, E., Side, J., and Harris, R. Thermal-diffusion and diffusion-thermo effects on combined heat and mass transfer of a steady MHD convective and slip flow due to a rotating disk with viscous dissipation and Ohmic heating. International Communications in Heat and Mass Transfer, 35, 908-915 (2008) |
| [21] | Affiy, A. A. Similarity solution in MHD: effects of thermal diffusion and diffusion thermo on free convective heat and mass transfer over a stretching surface considering suction or injection. Communications in Nonlinear Science and Numerical Simulation, 14, 2202-2214 (2009) |
| [22] | Anwar, B. O., Bakier, A. Y., and Prasad, V. R. Numerical study of free convection magneto- hydrodynamic heat and mass transfer from a stretching surface to a saturated porous medium with Soret and Dufour effects. Computational Materials Science, 46, 57-65 (2009) |
| [23] | Sallam, N. Thermal diffusion and diffusion-thermo effects on mixed convection heat and mass transfer in porous medium. Journal of Porous Media, 13(4), 331-345 (2010) |
| [24] | Kuznetsov, A. V. and Nield, D. A. Double-diffusive natural convective boundary-layer flow of a nanofluid past a vertical plate. International Journal of Thermal Sciences, 50, 712-717 (2011) |
| [25] | Ishak, A. and Nazar, R. Unsteady mixed convection boundary layer flow due to a stretching vertical surface. The Arabian Journal for Science and Engineering, 31, 165-182 (2006) |
| [26] | Zaimi, K., Ishak, A., and Pop, I. Stretching surface in rotating viscoelastic fluid. Applied Mathe- matics and Mechanics (English Edition), 34(8), 945-952 (2013) DOI 10.1007/s10483-013-1719-9 |
| [27] | Rani, H. P., Reddy, G. J., and Kim, C. N. Transient analysis of diffusive chemical reactive species for couple stress fluid flow over vertical cylinder. Applied Mathematics and Mechanics (English Edition), 34(8), 985-1000 (2013) DOI 10.1007/s10483-013-1722-6 |
 2014, Vol. 35
2014, Vol. 35








































