1 Introduction

The bilevel problem and mathematical program problem with equilibrium constraint repre- sent important classes of optimization problems which have been wildly investigated in a large number of articles and books. Recently,Moudafi^[1] studied a class of bilevel monotone equilib- rium problems in Hilbert spaces and suggested an iterative algorithm to compute approximate solutions of the problem and proved the weak convergence of the iterative sequence generated by the algorithm. Since then,many authors have further introduced and studied the bilevel mixed equilibrium problem (BMEP),the bilevel pseudomonotone equilibrium problem,and the bilevel generalized mixed equilibrium problems (BGMEP) in finite dimensional spaces and Banach spaces,respectively. For example,see ^{[2, 3, 4, 5, 6, 7, 8, 9, 10, 11]} and the references therein.

In this paper,we introduce and study a new class of BGMEP involving set-valued mappings in topological vector spaces. By using a minimax inequality due to Ding and Tan^[12],some existence theorems of solutions for the generalized mixed equilibrium problems (GMEP) and BGMEP are proved under quite mild conditions. The behavior of the solution set for the problems are also discussed. These results are new and generalize some results in this field.

Let E be a Hausdorff topological vector space with dual space E*,and let h·,·i denote the duality pairing between E* and E. Let C be a closed convex subset of E,and C(E*) denotes the family of all compact subsets of E*. Let F,H : E*×C×C → R and Φ, Ψ,φ,ψ: C×C → R be real-valued functions,N,M : E* × E* → E* be single-valued mappings,and A,T,Q,S :C → C(E*) be set-valued mappings. We consider the following BGMEP involving bifunctions and set-valued mappings:

where S_Φ,φ^F,N,A,T is the solution set of the following GMEP involving bifunctions and set-valued mappings:

Case I If ≡ Φ ≡ 0,then the BGMEP (1)-(2) reduce to the following BGMEP involving bifunctions and set-valued mappings:

where S_Φ,φ^F,N,A,T is the solution set of the following GMEP involving bifunctions and set-valued mappings:

The BGMEP (3)-(4) were introduced and studied in Banach spaces by Ding et al.^[6].

Case II If for given !,b! ∈ E* and η,bη : C × C → E,let F(N(u,v),x,y) = hN(u,v) − !,η(y,x)i and ,then the BGMEP (1)-(2) reduce to the following bilevel generalized mixed variational-like inequality problem (BGMVIP): for given !,! ∈ B*,

where S_Φ,φ,η^F,N,A,Tis the solution set of the following generalized mixed variational-like inequality problem (GMVIP):

The BGMVIP (5)-(6) were introduced and studied by Ding^{[4, 5]} in reflexive Banach spaces, which include the BMEP (1.3) introduced and studied by Chen et al.^[11] as special cases.

For suitable choice of Φ, ,H,F,M,N,A,T ,Q,S,,and ',it is easy to see that the BGMEP (1)-(2) include a lot of BGMEP,BGMVIP,GMEP,and GMVIP studied by many authors as special cases. For example,see [1 24] and the references therein.

2 Preliminaries

Definition 2.1 Let X and Y be topological spaces. A set-valued T : X → 2^Y is said to be

(i) upper semicontinuous if for each closed set D ⊆ Y ,the set T⁺¹(D) = {x ∈ X : T (x)∩D ≠∅ } is closed in X;

(ii) lower semicontinuous if for each open set D ⊆ Y ,the set T⁺¹(D) is open in X;

(iii) continuous if it is both upper and lower semicontinuous.

Definition 2.2 Let C be a closed convex subset of a topological vector space E. The bifunction Φ : C × C → R is said to be monotone if

Definition 2.3 Let C be a closed convex subset of a topological vector space E. Let N : E* × E* → E* be a single-valued mapping,A,T : C → C(E*) be set-valued mappings,and F : E* × C × C → R be a real-valued function. F is said to be monotone with respect to N,A, and T if

.

Remark 2.1 For the example of Definition 2.3,the reader may consult Remark 2.2 in Ref. ^[6].

Definition 2.4 Let E be a topological vector space. The bifunction ' : E ×E → R is said to be skew-symmetric if

.

For the properties and applications of the skew-symmetric bifunction,the reader may consult Antipin^[25].

Lemma 2.1^[26] Let X and Y be topological spaces and T : X → 2^Y be a set-valued mapping.

(i) If X is compact and T is upper semicontinuous with compact values,then T (X) is compact.

(ii) If Y is compact and T is closed,then T is upper semicontinuous.

(iii) If T is upper semicontinuous with closed values,then T is closed.

The following results are Theorem 7.3.11 and Theorem 7.3.14 of Klein and Thompson^[27].

Lemma 2.2 Let X,Y,and Z be topological spaces. Let F : X → 2^Y and G : Y → 2^Z be set-valued mappings.

(i) If F and G are upper semicontinuous,then G ◦ F : X → 2^Z is upper semicontinuous.

(ii) If F and G are lower semicontinuous,then G ◦ F : X → 2^Z is lower semicontinuous.

Lemma 2.3 Let I be an index set. Let X and Yi,i ∈ I be all topological spaces. For each i ∈ I,let Fi : X → 2^Yi be set-valued mappings. Let F = be defined by F(x) = (x). If each Fi is upper continuous with compact values,then F is also upper semicontinuous with compact values with respect to the product topology on .

Lemma 2.4^[28] Let X and Y be two topological spaces. Let F : X×Y → R be a bifunction and S : X → 2^Y be a set-valued mapping with nonempty values and let m(x) = .

(i) If F and S are both lower semicontinuous,then m is also lower semicontinuous.

(ii) If F is upper semicontinuous and S is upper semicontinuous with compact values,then m is also upper semicontinuous.

Lemma 2.5 Let C be a nonempty convex subset of a topological vector space E. Let N : E* × E* → E* and A,T : C → C(E*) be upper continuous. Let F : E* × C × C → R such that for each fixed y ∈ C,(u,x) → F(u,x,y) is upper continuous. Then,for each (x,y) ∈ C×C, there exists (u,v) ∈ A(x) × T (x) such that

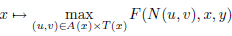.Furthermore,the mapping is upper semicontinuous.

Proof Since N : E* × E* → E* is upper semicontinuous and for each y ∈ C,(u,x) → F(u,x,y) is upper semicontinuous,it follows from Lemma 2.2 that for each y ∈ C,the mapping ((u,v),x) 7→ F(N(u,v),x,y) is also upper semicontinuous. By Lemma 2.3,the mapping A×T : C → C(E*)×C(E*) defined by (A×T )(x) = A(x)×T (x) is upper semicontinuous with compact values. Since for each x ∈ C,A(x) × T (x) is compact in E* × E*,it follows that there exists (u,v) ∈ A(x)×T (x) such that . It follows from Lemma 2.4 that the mapping 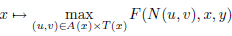is upper semicontinuous.

The following result is a special case of Theorem 1 of Ding and Tan^[12] (Also see Lemma 2.7 of Ding et al.^[6]).

Lemma 2.6 Let C be a nonempty convex subset of a topological vector space and let f : C × C → [−∞,+∞] such that

(i) f(x,x) > 0 for each x ∈ C;

(ii) for each y ∈ C,x ↔ f(x,y) is upper semicontinuous on each nonempty compact subset of C;

(iii) for each x ∈ C,y ↔ f(x,y) is convex;

(iv) there exists a nonempty compact subset K of C and y ∈ K such that f(x,y) < 0, ∀x ∈ C \ K. Then,there exists a point bx ∈ K such that f(bx,y) > 0 for all y ∈ C.

3 Behavior of solution set of GMEP (2)

Theorem 3.1 Let C be a closed convex subset of topological vector space E. Let F : E* × C × C → R,N : E* × E* → E*,A,T : C → C(E*),Φ : C × C → R,and φ : B × B → R satisfy the following conditions:

(i);

(ii) Φ is monotone and F is monotone with respect to N,A,and T ;

(iii) Φ is upper semicontinuous in the first argument and is convex and lower semicontinuous in the second argument;

(iv) for each y ∈ C,((u,v),x) ↔ F(N(u,v),x,y) is upper semicontinuous and for each z ∈ C and (u,v) ∈ A(z) × T (z),y ↔ F(N(u,v),z,y) is convex and lower semicontinuous;

(v) A and T are both upper semicontinuous;

(vi) ' is skew symmetric and continuous,and ' is convex in the first argument.

Then,there exists x ∈ C such that

if and only if Furthermore,the solution set S_Φ,φ^F,N,A,T of the GMEP (2) is a closed convex subset of C.

Proof For any y ∈ C,define two mappings G and P as follows:

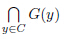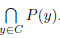In order to show that the conclusion of Theorem 3.1 holds,we only need to show = . Since Φ is monotone,we have

Since F is monotone with respect to N,A,and T ,we have

Since ' is skew symmetric,we have

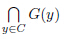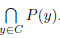Hence,if x ∈ G(y),then x ∈ P(y). It follows that ⊆ . Conversely,if there exists x ∈ 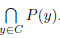,but x ≠ 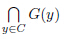,then we have and there exists y ∈ C such that It follows that Let xt = ty + (1 − t)x = x + t(y − x),t ∈ ^{[0, 1]}. Then,xt ∈ C. It follows from (9) that Since for each y ∈ C,((u,v),x) ↔ F(N(u,v),x,y) is upper semicontinuous and each A(xt) × T (xt) is compact,it follows that for each t ∈ (0,1],there exists (ut,vt) ∈ A(xt) × T (xt) such that 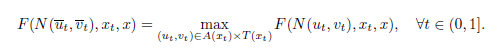By (12),we have Let Ω = {x_t}t∈[0 1]. Then, is compact. Since A and T are both upper semicontinuous with compact values,it follows from Lemma 2.1 that A(Ω) × T (Ω)is compact in E* × E*. Noting (ut,vt)t2^{[0, 1]} ⊂ A(Ω)× T (Ω)and lim t!0 xt → x,without loss of generality,we can assume that there exists (u,v) ∈ E*×E* such that (ut,vt) → (u,v) and (u,v) ∈ A(x)×T (x). Since for each y ∈ C,x ↔ Φ(x,y) and ((u,v),x) ↔ F(N(u,v),x,y) are upper semicontinuous,x ↔ −Φ(x,y) and ((u,v),x) ↔ −F(N(u,v),x,y) are lower semicontinuous. As ' is continuous,by (13),we have that

Hence,there exists t* ∈ (0,1] such that

It follows that By (13),we have Since by condition (iii) of Theorem 3.1,for each t ∈ (0,t*],x ↔ F(N(ut,vt),xt,x) is convex,Φ is convex in the second argument,' is convex in the first argument,and xt = ty + (1 − t)x. It follows from (14) and (15) that for each t ∈ (0,t*], Hence,for t ∈ (0,t*],we obtain Φ(xt,xt) + F(N(ut,vt),xt,xt) < 0,which contradicts the assumption that Φ(x,x) + F(N(u,v),x,x) > 0,for all x ∈ C and (u,v) ∈ A(x) × T (x). Therefore,we have = . 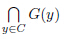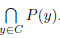It is easy to see that S_Φ,φ^F,N,A,T = 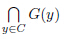. 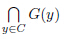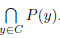Therefore, S_Φ,φ^F,N,A,T = = is the solution set of GMEP (2). By the definition of P,for each y ∈ C,we have Since for each y ∈ C and (w,z) ∈ A(y) × T (y),x ↔ F(N(w,z),y,x),x ↔ Φ(y,x),and x ↔ '(x,y) are all convex and lower semicontinuous,it follows that for each y ∈ C,the set {x ∈ C : F(N(w,z),y,x) + '(x,y) 6 '(y,y)} is closed and convex. Hence,P(y) and 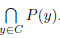are both closed convex subsets of C. If the set 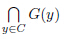= 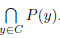is nonempty,then there exists bx ∈ C such that Since for each y ∈ C,((u,v),bx) ↔ F(N(u,v),bx,y) is upper semicontinuous and A(bx)× T (bx) is compact,it follows that there exists (bu,bv) ∈ A(bx) × T (bx) such that It follows from (18) and (19) that there exist bx ∈ C and (bu,bv) ∈ A(bx) × T (bx) such that

Therefore,the solution set S_Φ,φ^F,N,A,T of GMEP (2) is closed and convex in C.

Remark 3.1 Theorem 3.1 improves and generalizes the corresponding results in Refs. ^{[2, 3, 4, 5, 6, 7]} to topological vector spaces.

Theorem 3.2 Let C be a closed convex subset of topological vector space E and K be a compact subset of E with C ∩ K 6= ?. Let F : E* × C × C → R and Φ,' : E × E → R be real-valued functions. Let N : E* ×E* → E* be single-valued mappings and A,T : C → C(E*) be set-valued mappings. Suppose that the following conditions are satisfied:

(i) Φ(x,x) + F(N(u,v),x,x) > 0,∀x ∈ C,(u,v) ∈ A(x) × T (x);

(ii) Φ is monotone and F is monotone with respect to N,A,and T ,and for each y ∈ C, ((u,v),x) ↔ F(N(u,v),x,y) is upper semicontinuous;

(iii) Φ is upper semicontinuous in the first argument and is convex and lower semicontinuous in the second argument and for each x ∈ C and (u,v) ∈ A(x) × T (x),y ↔ F(N(u,v),x,y) is convex;

(iv) A and T are both upper semicontinuous;

(v)φ is skew symmetric and continuous,and ' is convex in first argument;

(vi) there exists y ∈ C ∩ K such that

There exist bx ∈ C ∩ K and (bu,bv) ∈ A(bx × T (bx) such that

and bx ∈ C ∩ K and (bu,bv) ∈ A(bx × T (bx) is a solution of the GMEP (2). Furthermore,the solution set of GMEP (2) is a nonempty compact and convex subset in C.

Proof Define a bifunction f : C × C → R as follows:

By the definition of f and condition (i) of Theorem 3.2,we have f(x,x) > 0,∀x ∈ C and condition (i) of Lemma 2.6 is satisfied. Since for each y ∈ C,((u,v),x) ↔ F(N(u,v),x,y) is upper semicontinuous,and A × T : C ↔ C(E) is upper semicontinuous with compact values,it follows from Lemma 2.5 that for each y ∈ C,x ↔ max (u,v)2A(x)×T(x) F(N(u,v),x,y) is upper semicontinuous. Noting that Φ is upper semicontinuous in the first argument and ' is continuous,we have that for each y ∈ C,x ↔ f(x,y) is upper semicontinuous and so condition (ii) of Lemma 2.6 is satisfied. Since for each x ∈ C and (u,v) ∈ A(x) × T (x), y ↔ F(N(u,v),x,y) is convex,for any y1,y2 ∈ C and t ∈ ^{[0, 1]},we have Hence,for each x ∈ C,y ↔ max (u,v)2A(x)×T(x) F(N(u,v),x,y) is convex. Note that for each x ∈ C, y ↔ Φ(x,y) and y ↔ '(y,x) are both convex. We have that for each x ∈ C,y ↔ f(x,y) is convex. Condition (iii) of Lemma 2.6 is then satisfied. By condition (vi) of Theorem 3.2,there exists a point y ∈ C ∩ K such that f(x,y) < 0,∀x ∈ C \ K and condition (iv) of Lemma 2.6is satisfied. By Lemma 2.6,there exists a point bx ∈ C such that f(bx,y) > 0,∀y ∈ C. By the definition of f,we obtain Since for each y ∈ C,(N(u,v),bx,y) ↔ F(N(u,v),bx,y) is upper semicontinuous and A(bx)×T (bx) is compact in E* × E*,there exists (bu,bv) ∈ A(bx) × T (bx) such that It follows from (21) and (22) that there exist bx ∈ C ∩ K and (bu,bv) ∈ A(bx × T (bx) such that

i.e.,bx ∈ C∩K and (bu,bv) ∈ A(bx)×T (bx) is a solution of the GMEP (2). It follows from Theorem 3.1 that the solution set S_Φ,φ^F,N,A,T of GMEP (2) is a nonempty compact and convex subset in C.

4 Behavior of solution set of BGMEP (1)-(2)

Theorem 4.1 Let C be a closed convex subset of topological vector space E and K be a compact subset of E with C ∩ K 6= ?. Let F,H : E* × C × C → R,Φ, : C × C → R,and φ,: E×E → R be real-valued functions. Let N,M : E*×E* → E* be single-valued mappings and A,T,Q,S : C → C(E*) be set-valued mappings. Suppose that the following conditions are satisfied:

(i) Φ,F,N,A,T,and ' satisfy all the conditions of Theorem 3.2;

(ii) (x,x) + H(M(u,v),x,x) > 0,∀x ∈ C,(u,v) ∈ Q(x) × S(x);

(iii) is monotone and H is monotone with respect to M,Q,and S,and for each y ∈ C, ((u,v),x) ↔ H(M(u,v),x,y) is upper semicontinuous;

(iv) is upper semicontinuous in the first argument and is convex and lower semicontinuous in the second argument and for each x ∈ C and (u,v) ∈ Q(x) × S(x),y ↔ H(M(u,v),x,y) is convex;

(v) Q and S are both upper semicontinuous;

(vi) is skew symmetric and continuous,and is convex in the first argument.

Then,the solution set of the BGMEP (1)−(2) is a nonempty compact and convex subset in C.

Proof From condition (i) and Theorem 3.2,we have that the solution set S_Φ,φ^F,N,A,T of GMEP (2) is a nonempty compact and convex subset in C. Define a bifunction f : S_Φ,φ^F,N,A,T × S_Φ,φ^F,N,A,T → R as follows:

. By the similar argument as in Theorem 3.2,it is easy to check that f satisfies conditions (i),(ii), and (iii) of Lemma 2.6. Note that S_Φ,φ^F,N,A,T is a compact and convex subset of C. Hence, condition (iv) of Lemma 2.6 is satisfied trivially. By Lemma 2.6,there exists x* ∈ S_Φ,φ^F,N,A,T such that )

Since for each y ∈ C,((u,v),x*,y) ↔ H(M(u,v),x*,y) is upper semicontinuous and Q(x*) × S(x*) is compact in E* × E*,there exits (u*,v*) ∈ Q(x*) × S(x*) such that

It follows from (23) and (24) that there exist x* ∈ S_Φ,φ^F,N,A,T and (u*,v*) ∈ Q(x*) × S(x*) such that

. Hence,the solution set of the BGMEP(1)-(2) is nonempty. By the same argument as in Theorem 3.1,we can prove that the solution set of the BGMEP(1)-(2) is also a nonempty closed and convex subset in S_Φ,φ^F,N,A,T and hence it is a nonempty compact and convex subset in C.