Shanghai University
Article Information
- Xiang-jiang YUAN, Zhi-yong LIU, Qing SHEN, Guo-liang LI. 2014.
- Theoretical investigation on shocklets in compressible boundary layers
- Appl. Math. Mech. -Engl. Ed., 35(8): 935-946
- http://dx.doi.org/10.1007/s10483-014-1843-7
Article History
- Received Jun. 27, 2013;
- Revised Oct. 11, 2013
The shock wave is one of the typical nonlinear phenomena distinguishing incompressible and compressible flows. Shocklets are a series of shock waves with mild intensity; they share all the properties with shock waves. It is well known that shocklets may exist in isotropic compressible turbulence and shear flows. However,it is not clear whether shocklets may appear in laminar boundary layer. With regard to the shocklets in shear flows,several problems are still to be solved,for example,what are the conditions to form the shocklets,what is the configuration of the shocklets,how does a shocklet evolve,and so on. The existing investigations are still not able to answer these questions,which are of great significance to the study of compressible flow because they are involved in nonlinear wavy phenomena which are quite different from those in incompressible flows. Moreover,the answers to these questions are crucial not only for the exploration of nonlinear stability theory but also for the understanding of flow transition of compressible flows.
Fu and Ma [1] first mentioned the phenomenon of shocklets in two-dimensional mixing layers in 1996. However,little attention had been paid. In 1999 Yuan and Zhou [2] proposed the possibility that the shocklets might appear in the transition of supersonic flows. Since then the interest on shocklets has been aroused and several progresses have been achieved. In 2000,Shen et al. [3] numerically simulated the shocklets in boundary layer with a leading edge shock. Huang and Zhou [4] studied the disturbance evolution in a two-dimensional supersonic boundary layer by numerical simulations,and found that the shocklets are close to the wall. By tracking the entropy increase of mass point,they believed that what the tracked point passed through was shocklet. According to the variation of the relative Mach number,they further concluded that the shocklets were normal shock waves. Cao and Zhou [5] illustrated that the shocklets could appear when the disturbance amplitude in the supersonic boundary layer was large enough. According to previous numerical simulations[4, 5] ,the convective velocity of shocklet is the same as Tollmien-Schlichting (T-S) waves. Since the velocity of T-S wave is close to the far-field velocity and so is the mean velocity at the edge of boundary layer,the relative Mach number of the shocklet to wavefront would be less than 1. Therefore,shocklet can only exist in the nearwall region. Because of the limitation of experimental methods and technologies,experimental study of shocklet in compressible boundary layer flows has not been reported.
In order to understand the shocklets in compressible boundary layers more comprehensively and lay the foundations of numerical simulation,we investigate theoretically on the formation and evolvement mechanisms of shocklets. Discussions are made on how T-S waves induce shocklets and what is the role of viscosity in the process of shocklets formation. In the following statement, it will be noted that the shock wave is equivalent to shocklet when the properties are discussed.2 Characteristics of shock waves
The properties of shock waves will be disclosed before the discussion on the types of disturbing waves which may develop to shock waves. According to Whitham’s definition [6] ,the perturbations are named hyperbolic waves if they are governed by a hyperbolic equation:
Firstly,the shock wave has a possible weak solution of quasi-linear hyperbolic equations as with the initial condition A weak solution U (x,t) satisfying (3) and (4) also satisfies the Rankine-Hugoniot relation: in which U+ and U- denote the right and left limit values of discontinuity U (x,t) on the two sides,and D is called the discontinuity slope. As a matter of fact,when U (x,t) represents a shock wave,D is the generalized eigenvalues,i.e.,the velocity components of a shock wave. It is clear that the velocity of a shock wave is determined only by the limit values of U (x,t). Hence,the shock wave is a hyperbolic wave.Secondly,if U (x,t) is the absolute velocity of fluid,and Vr denotes the absolute value of fluid velocity relative to the shock wave,the shock wave theory gives
where the unit vector n is perpendicular to the wavefront and parallel to the propagating direction of the shock wave. Subscripts ‘0’ and ‘1’ in (6) represent the undisturbed fluid before the shock wave and disturbed fluid after it,respectively. As Vr0 is supersonic,and Vr1 is subsonic,Vr0 − Vr1 is always positive. Therefore,it can be deduced from (6) that the velocity change caused by the shock wave is vertical to the wavefront,i.e.,the direction of disturbing velocity parallels the direction in which the wavefront propagates. Thus,we can infer that the shock wave is a longitudinal wave. 2.1 Hyperbolic waves in fluidsAs discussed above,the shock wave is hyperbolic and longitudinal. Therefore,it is essential to investigate the hyperbolic waves in fluids to figure out which waves can evolve to shock waves. For convenience,we consider the ideal,adiabatic,and isentropic gas flow which is governed by the following equations:
in which p,ρ,t,and k are the pressure,density,time,and ratio of specific heats,respectively. The vector V is the velocity with components U ,V ,W in the x-,y-,and z -directions.
Disturbances are added to the mean flow,and the total fields  can be
decomposed into mean values U ,V ,W ,P ,ρ and perturbation quantities u,v,w,p,ρ′
as
can be
decomposed into mean values U ,V ,W ,P ,ρ and perturbation quantities u,v,w,p,ρ′
as
Substituting (10) into (7),(8) and (9),we can obtain the following equations after linearization:
We assume that the disturbances propagate as traveling waves,and let α,β,and γ be the wave numbers in the x-,y-,and z -directions,ω be the frequency. The amplitudes of the disturbances (u,v,w,p,ρ) are denoted as (u1 ,v1,w1,p1,ρ1). Thus,
Rewriting (12)-(15) with the expression above under the isentropic and perfect-gas assumptions,we can obtain
in which
and c is the sound speed. We know that the solution of (17) is nonzero if and only if the determinant of the above coefficient matrix is zero. Thus,setting the determinant be zero yields
(18) implies that two types of solutions exist,with the first one having a triple root as follows:
The second type contains two solutions of the following equation: which givesFirstly,we discuss the characteristics of hyperbolic wave which is defined by the first type of solution. (19) is divided by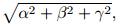 ,then becomes
(23) and (16) indicate that the phase velocity of this hyperbolic wave equals the velocity component of the mean flow field in the direction of wave propagation. Substituting (19) into
momentum equations in (17),we can getApplying the substitution in the continuity equation in (17) and combining (24),one can obtain
which implies that the propagating direction of hyperbolic wave is perpendicular to the direction
in which the fluid moves. Hence,this type of hyperbolic wave is a transverse wave. More
importantly,from (24) we know that the hyperbolic wave cannot result in any pressure changes.
Therefore,the characteristics discussed above indicate that this type of hyperbolic wave cannot
evolve to a shock wave.
,then becomes
(23) and (16) indicate that the phase velocity of this hyperbolic wave equals the velocity component of the mean flow field in the direction of wave propagation. Substituting (19) into
momentum equations in (17),we can getApplying the substitution in the continuity equation in (17) and combining (24),one can obtain
which implies that the propagating direction of hyperbolic wave is perpendicular to the direction
in which the fluid moves. Hence,this type of hyperbolic wave is a transverse wave. More
importantly,from (24) we know that the hyperbolic wave cannot result in any pressure changes.
Therefore,the characteristics discussed above indicate that this type of hyperbolic wave cannot
evolve to a shock wave.
Then,we consider the second type of hyperbolic wave defined by (21) and (22). Similarly,
dividing the two equations with ,we can get
,we can get
In fact,discontinuity can be viewed as a form of hyperbolic wave. The fluid on both sides of discontinuity obeys the mass and momentum conservation laws as
which can be rewritten as(31) implies that the relative velocity change (Vr0 −Vr1 ) results from the perturbation of pressure

Essentially,the shock wave is a possible solution of quasi-linear hyperbolic equations and therefore,the investigation of the formation mechanism of a shock wave starts with the study of hyperbolic wave. Although (2) is the simplest one of hyperbolic equations,the prototype of hyperbolic equation is regarded as (1) conventionally. (1),which depicts the propagation of sound wave in fluid,was first deduced by Euler from fluid dynamic equations in 1759. Prior to obtaining the equation,one assumption was adopted that the disturbance of sound wave is so weak that the sound speed always remains a constant in propagation. For convenience,we introduce a nondimensional denseness as [7]





The following equations can be obtained from the shock wave theory:
in which

The formation of a shock wave is symbolized by the increase of entropy. (45) indicates that
the change of entropy must be considered if  is not negligible. And if the intensity is so weak that
is not negligible. And if the intensity is so weak that  can be ignored,the propagation can be treated as isentropic. Keeping the first-order term of
can be ignored,the propagation can be treated as isentropic. Keeping the first-order term of 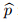 in (44) and eliminating higher-order terms,we can expect the equation as
in (44) and eliminating higher-order terms,we can expect the equation as
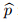 will be taken into consideration.3 Relation between T-S wave and shock wave
will be taken into consideration.3 Relation between T-S wave and shock waveAccording to the oscillation equation,linear hyperbolic waves may be periodic,or nonperiodic. Even for a periodic wave,the wave speed is independent of frequency or wave number, which is the same with nonlinear hyperbolic wave. While different from nonlinear wave,whose speed depends on the local fluid state,the wave speed of linear periodic wave relies only on the state of fluid in the undisturbed region. In fact,the speed of a shock wave is determined by the states of fluid ahead and behind. Dispersive wave must be periodic,and the speed relies on the wave number. The frequency and wave number are normally not influenced by the local flow except that strong nonlinearity takes effect. Therefore,the typical dispersive wave cannot induce the shock wave because accumulative aberrance will not be produced when local flow imposes no effect on the wave.
Conventionally the T-S wave is regarded as a dispersive wave. It may exist in the elliptic system of incompressible flow,or hyperbolic system of hypersonic flow. Assuming that the normal coordinate y parallels the wavefront,and the streamwise and spanwise coordinates x and z are perpendicular to the wavefront. T-S waves of disturbing velocity components can be expressed as
in which α and β denote the wave numbers in x- and z -directions,ω is the frequency of disturbing wave. Additionally,we assume that the disturbance travels in stationary atmosphere,or the fluid in which normal flow is uniform (similar to the flow at the edge of planar boundary layer).Considering the two-dimensional incompressible flow,which actually is one-dimensional for planar wave when the normal flow is uniform,one can write the continuity equation as
It can be inferred from (48) that one-dimensional T-S wave does not exist in the compressible flow. One-dimensional wave must be longitudinal,strictly speaking therefore,T-S wave is not longitudinal wave at least. When we consider the three-dimensional incompressible flow,the continuity equation becomes(49) indicates that the T-S wave may exist as a transverse wave.For a two-dimensional compressible flow,we suppose that the pressure and density disturbances share the same forms with velocity fluctuation in (47) as
For convenience,we consider the two-dimensional stationary compressible fluid and the continuity equation and momentum equation of x-component areDefine
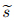 is denseness as defined previously. The subscript ‘0’ represents the basic flow,and c
0 is
the acoustic velocity of the undisturbed flow. It can be easily deduced from (53) and (54) thatObviously (55) and (56) are one-dimensional sound wave equations. Therefore,the T-S wave
in compressible flows is hyperbolic and longitudinal,which means it may evolve to shock waves
under certain specific conditions.
is denseness as defined previously. The subscript ‘0’ represents the basic flow,and c
0 is
the acoustic velocity of the undisturbed flow. It can be easily deduced from (53) and (54) thatObviously (55) and (56) are one-dimensional sound wave equations. Therefore,the T-S wave
in compressible flows is hyperbolic and longitudinal,which means it may evolve to shock waves
under certain specific conditions.As a matter of fact,in 1965 Mack [8] proposed the possibility for T-S wave to induce the shock wave. Relative Mach number was defined as

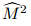 > 1 and elliptic for
> 1 and elliptic for
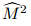 < 1,which
theoretically guarantee the possibility of induction.
< 1,which
theoretically guarantee the possibility of induction.
It can be noted that Mack’s theory is only valid under some assumptions and in some regions
with specific conditions. According to Mack’s definition,
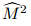 > 1 corresponds to two different
regions in the boundary layer with
> 1 corresponds to two different
regions in the boundary layer with
 > 1 and
> 1 and
 < −1. The former corresponds to the regime
outside the critical layer (outer layer) and the latter lies between the wall and the critical layer
(inner layer). Thus,the induction of shock wave may only occur in these two regions.
< −1. The former corresponds to the regime
outside the critical layer (outer layer) and the latter lies between the wall and the critical layer
(inner layer). Thus,the induction of shock wave may only occur in these two regions.
In order to investigate the behavior of a T-S wave,we conduct the linear stability analysis on
the planar boundary layer with Mach number 4.5 of incoming flow
[9]
. Combining the theoretical
analysis above and numerical calculation,the following conclusions can be achieved: (i) In the
neighborhood of critical layer,the absolute value of relative Mach number is smaller than 1.
The critical layer lies at y = 9.6 which is a non-dimensional length scaled by a reference length  is always true in the boundary layer,T-S wave cannot
evolve to slow acoustic wave,and thus the shock wave would not appear out of the critical layer.
(iii) T-S wave may convert to a fast acoustic wave and therefore the T-S wave can induce shock
wave which travels rightward. The fast acoustic wave appears at y = 6.97,and accordingly the
shock wave is induced by T-S wave in the neighborhood.
4 Viscous effect on formation of shock wave
is always true in the boundary layer,T-S wave cannot
evolve to slow acoustic wave,and thus the shock wave would not appear out of the critical layer.
(iii) T-S wave may convert to a fast acoustic wave and therefore the T-S wave can induce shock
wave which travels rightward. The fast acoustic wave appears at y = 6.97,and accordingly the
shock wave is induced by T-S wave in the neighborhood.
4 Viscous effect on formation of shock wave
In the discussion above,the sound speed is emphatically supposed to be constant while actually it is not always true. Denoting


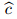 is the same order of magnitude as
is the same order of magnitude as 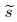 but always smaller than it. It
seems that even the weakest disturbance would be compressed to a shock wave. While in fact,
it is not true because we neglect the effect of viscosity. Consider the inviscid Burgers equation
We know from the characteristic line theory that at time t = 0,each point x
0,where a characteristic line x(t) starts,satisfiesThe Riemann invariant keeps constant along this characteristic line. For the one-dimensional
case,the solution is the Riemann invariant and the characteristic line is linear. If only one
characteristic line passes through each point (x,t),then the solution can only beSpecially,a smooth initial-value function can be written asand it is easy to prove that when t ≤ 1/2,the characteristic lines x − x0 = u
0(x0)t,which start
from any two different points on 0 ≤ x ≤ 1,do not intersect. When t > 1/2,there always
exist two points on 0 ≤ x 6 1/2,whose characteristic lines intersect. So to speak,the solution
of inviscid Burgers equation may be discontinuous even if the initial-value function is smooth.
Actually,for (61),the characteristic lines will eventually intersect as long as the initial-value
function u0(x) is descendent in some region.
but always smaller than it. It
seems that even the weakest disturbance would be compressed to a shock wave. While in fact,
it is not true because we neglect the effect of viscosity. Consider the inviscid Burgers equation
We know from the characteristic line theory that at time t = 0,each point x
0,where a characteristic line x(t) starts,satisfiesThe Riemann invariant keeps constant along this characteristic line. For the one-dimensional
case,the solution is the Riemann invariant and the characteristic line is linear. If only one
characteristic line passes through each point (x,t),then the solution can only beSpecially,a smooth initial-value function can be written asand it is easy to prove that when t ≤ 1/2,the characteristic lines x − x0 = u
0(x0)t,which start
from any two different points on 0 ≤ x ≤ 1,do not intersect. When t > 1/2,there always
exist two points on 0 ≤ x 6 1/2,whose characteristic lines intersect. So to speak,the solution
of inviscid Burgers equation may be discontinuous even if the initial-value function is smooth.
Actually,for (61),the characteristic lines will eventually intersect as long as the initial-value
function u0(x) is descendent in some region.Next,we consider the viscous Burgers equation
This equation can be derived from one-dimensional Navier-Stokes equation under a weakly nonlinear condition,which means that (65) correctly depicts real physical phenomena. In 1956, Lighthill[10] made a detailed discussion about the property of the solution of Burgers equation. Main conclusions are cited here: when Reynolds number Re = UL/υ << 1,the solution of (65) becomes that of diffusion equation; while for Re >> 1,the solution contains a structure of the shock wave if the initial-value function is sharply peak-like. For x > (2Revt)1/2the value of solution,u descends abruptly and forms a thin layer structure,which is a shock wave.However,this shock wave is no longer a discontinuous wavefront. The solution u(x,t) is not only single-valued but also continuous; and when t → ∞ its value descends less steeply. When the Reynolds number Re is neither too large nor too small,the thin layer does not exist in the solution u(x,t) for any initial values. Hence,we can infer that viscosity tends to flatten the solution because the viscosity impedes the disturbance like sound wave from developing to the shock wave. Conclusively,the shock wave is hard to form where a strong viscous effect exists. 5 Notes about shock waveBased on the discussion above,some remarks about the phenomena during the transformation from continuous wave to the shock wave are made as follows:
From (39) and (59),we know the velocity of disturbed fluid and the sound speed are both proportional to denseness. Thus,the source of disturbance cannot move too fast,otherwise the disturbance behind the wave cannot catch up with the wave accumulation produced by the source,unless the disturbing intensity of the source is equivalent to that of the shock wave.
As discussed previously,the sound wave or finite-amplitude disturbance is isentropic before evolving to the shock wave,and thus the mechanical energy does not lose and the wave propagates with constant amplitude under the inviscid assumption. When the disturbances accumulate and form the shock wave,as the entropy of fluid behind the wave increases,the mechanical energy of the shock wave is dissipated. Therefore,in the propagation of a shock wave,the strength weakens even if the effect of viscosity is not taken into consideration.
According to Whitham [6] ,the traveling velocity of the weak shock wave in the propagation is
which indicates that the gradients of temperature and velocity cannot match well. Thus,the wavefront of the weak shock wave in a non-uniform flow field is usually not planar.Although viscosity acts against the formation of the shock wave,Coleman [11] et al. made a comprehensive investigation in 1956 and proposed a statement that there exists a threshold value for the disturbance amplitude,above which the wave steepens in shape and tends to form the shock wave while below which the wave exhibits no such behaviors.
The discussion above has confirmed the possibility for T-S wave to form a shock wave,while
the configuration of the shock wave has not been identified. According to the theory of the shock
wave,its velocity depends on the flow fields immediately upstream and downstream. Under the
effect of viscosity,the mean flow field is not uniform in the normal direction. Therefore,if the
shock wave forms in the region of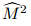 > 1,the propagating velocity usually changes because of
the non-uniformity of the normal mean flow field.
6 Conclusions
> 1,the propagating velocity usually changes because of
the non-uniformity of the normal mean flow field.
6 Conclusions
Conclusions are summarized based on the analysis above: (I) The shock wave is induced by nonlinear,hyperbolic,and longitudinal wave. (II) Hyperbolic wave cannot evolve to the shock wave in linear system,which is determined by the property of linear wave equation. (III) If the change of sound speed in the hyperbolic wave equation cannot be neglected,the shock wave can always form theoretically. (IV) In incompressible flows,T-S wave exhibits the characteristics of dispersion wave. (V) In compressible flows,T-S wave behaves as hyperbolic wave in the regions where the relative Mach number is larger than 1,which lays a theoretical foundation for T-S wave to develop to the shock wave under some specific conditions. (VI) Viscosity takes effect in two ways: impeding the formation of the shock wave and strengthening the dissipation of shock wave. Thus,the shock wave will be induced where viscous effect hardly works. (VII) The mechanical energy of shock wave dissipates even under the inviscid condition. (VIII) The relative velocity of continuous waves will be moderate to make sure that the shock wave is induced.
| [1] | Fu, D. X. and Ma, Y. W. Methods of group velocity controlling and numerical simulation of three dimensional planar mixing layer. Proceedings of Modern Mechanics and Science and Technology Progress Conference, China Academy of Mechanics, Beijing, 533–538 (1997) |
| [2] | Yuan, X. J. and Zhou, H. A numerical study for small amplitude T-S waves in a supersonic boundary layer. Appl. Math. Mech. -Engl. Ed., 21(12), 1211–1214 (2000) DOI 10.1007/BF02459212 |
| [3] | Shen, Q., Zhang, H. X., and Yuan, X. J. Numerical simulation of shock-lets within the supersonic boundary layer. Acta Aerodynamica Sinica, 18, 103–108 (2000) |
| [4] | Huang, Z. F. and Zhou, H. Evolution of a 2-D disturbance in a supersonic boundary layer and the generation of shocklets. Appl. Math. Mech. -Engl. Ed., 25(1), 1–8 (2004) DOI 10.1007/BF02437288 |
| [5] | Cao, W. and Zhou, H. A numerical investigation of the evolution of 2-D disturbances in hypersonic boundary-layers and the effect on the flow structure due to the existence of shocklets. Science in China (Series G ), 47(2), 244–255 (2004) |
| [6] | Whitham, G. B. On the propagation of weak shock wave. Journal of Fluid Mechanics, 1, 290–318 (1956) |
| [7] | Liepmann, H. W. and Roshko, A. Elements of Gasdynamics, Wiley, New York (1957) |
| [8] | Mack, L. M. Stability of the compressible laminar boundary layer according to a direct numerical simulation. Recent Developments in Boundary Layer Research, 97, 329–362 (1965) |
| [9] | Yuan, X. J., Tian, J. W., Shen, Q., and Li, Y. Shocklets in compressible flows. Appl. Math. Mech. -Engl. Ed., 34(12), 1453–1464 (2013) DOI 10.1007/s10483-013-1759-7 |
| [10] | Lighthill, M. J. Viscosity effects in sound waves of finite amplitude. Surveys in Mechanics (eds. Batchelor, G. K. and Davies, R. M.), Cambridge University Press, London (1956) |
| [11] | Coleman, B. D., Herrera, I., and Truesdell, C. Wave Propagation in Dissipative Materials, Springer, New York (1965) |
 2014, Vol. 35
2014, Vol. 35




















































