Shanghai University
Article Information
- J. V. R. REDDY, D. SRIKANTH, S. K. MURTHY. 2014.
- Mathematical modelling of couple stresses on fluid flow in constricted tapered artery in presence of slip velocity-effects of catheter
- Appl. Math. Mech. -Engl. Ed., 35(8): 947-958
- http://dx.doi.org/10.1007/s10483-014-1848-7
Article History
- Received Jul. 18, 2013;
- Revised Feb. 1, 2014
It is widely known that,in blood vessel system stenosis may develop on the inner wall ofthe artery in various forms and at any location due to the accumulation of the fat components,excessive calcium,and abnormal intra-vascular growth. Due to this artery becomes thick whichnarrows down passage of fluid,a condition of the artery that is known as atherosclerosis. Thisleads to blockage of arteries,the origin of abnormal variability of blood pressure and variousflow characteristics. Various methods are available to treat atherosclerosis but catheterisationis the first form of endovascular treatment. Catheterisation is a process in which a lengthy thinversatile tube is inserted into the lumen of the artery using a guide-wire to clear the blockagesin the artery. One such procedure is balloon angioplasty. The blood flow characteristics sig-nificantly change due to the insertion of the catheter into the artery. Hence,the study of thecatheter effects in physiological fluid flow in clogged artery is very important. Based on the workof Sarkar and Jayaraman[ 1 ] catheter can be considered to be rigid if it is fairly thick. Further,depending upon the material properties an oscillating thin catheter will behave similarly as thatof thick catheter which is not affected by blood velocity inside the artery and hence does notoscillate. Based on the above literature,the study of variations in the blood flow characteristicsis undertaken from the point of view of fluid dynamics while treating atherosclerosis.
Several researchers used fluid mechanics to study the behaviour of physiological fluids invarious conditions. Rudolf and Paul[ 2 ] studied the mechanics of the duct by considering theperistaltic motion along the stationary cylinder when a catheter is introduced into it. Young and Tsai[ 3 ] considered a steady flow of blood in their study of flow characteristics in arterialstenosis.
In all the above mentioned studies,Newtonian behaviour of the blood has been modelled. Itis a known fact that at low shear rates,human blood exhibits non-Newtonian behaviour becauseof the suspension nature of the blood cells. Shukla et al.[ 4 ] studied the effect of stenosis usingCasson and power law fluid models. Srinivasachary and Srikanth[ 5 ] analyzed the steady flow ofmicropolar fluid through the catheterized artery in the presence of stenosis. Several other studieswere done considering the importance the non-Newtonian behaviour of the blood[ 6, 7 ]. However,the couple stress fluid theory developed by Stokes[ 8 ] represents blood flow reasonably well. Thecouple stress fluid model has been extensively used[ 9, 10, 11, 12 ] because of its relative simplicity indealing with the governing equations,when compared with that of other polar fluid models.This being a polar fluid,it accounts for all the features related to it. This fluid theory alsoincorporates all the effects of couple stresses and all other relevant characteristic. Further,theequations are similar to the Navier-Stokes equations,which facilitates a possible comparisonof the results with that obtained by the theory of non-polar fluids. The introduction of thesize dependent effect is the most important feature of the couple stress fluid. This effect is notpresent in the other viscous fluid theories. Hence,it is appropriate to model blood by using thecouple stress fluid.
In the aforementioned studies,the stenosis shape is assumed to be symmetric. But it isa known fact that stenosis is non-symmetric while it is growing. By taking this into accountresearchers[ 13, 14 ] studied blood flow through asymmetric stenosis. The flows through the un-symmetric stenosed tapered artery were discussed by Mekheimer and El Kot[ 15 ] and M and el[ 16 ].
Brunn[ 17 ] explained theoretically and Bennett[ 18 ] showed experimentally the likely presenceof the velocity slip at the boundary. Recently,Misra and Shit[ 19 ] considered the velocity slip atthe wall of the stenosed artery in their mathematical model which was used to study the bloodflow characteristics. Hence,it seems quite rational to consider the velocity slip at the wall ofstenosed artery in modelling of the blood flow dynamics.
In view of the above,authors intend to discuss the effect of asymmetric nature of the stenosis,catheter,slip velocity and tapered parameter on the physiological parameters like resistance tothe flow and shear stress at the wall,when blood is modelled by the couple stress fluid.2 Mathematical formulations2.1 Physical model of stenosed tapered artery
In the present study,the flow of couple stress fluid is considered in an annular region formedby two coaxial circular rigid tubes of finite length L. The radius of the catheter is denotedby rc,while the annular radius is denoted by r0. The flow is assumed to be homogeneous,axisymmetric,and incompressible. Further,it is flowing in an artery with asymmetric natureof the stenosis on the wall in the presence of catheter as shown in Fig. 1. The tapered artery withtapering angle φ is depicted in Fig. 2. ζ(=tan φ)is the tapered parameter. φ < 0 correspondsto the converging nature of the tapered artery,φ = 0 corresponds to the non-tapered nature ofartery,while the diverging nature of the tapered artery corresponds to φ > 0.
 |
| Fig. 1 2D view of physical model of stenosedartery with catheter |
 |
| Fig. 2 2D view of stenosed tapered arterywith catheter |
The mathematical representation of the tapered artery in the presence of stenosis is givenby[ 13 ]
with L0 representing the length of the artery up to the origin of the stenosis,and L1 representsthe total stenosis length. n(> 2)determines the stenosis shape(symmetric nature of thestenosis is obtained when n = 2). ε corresponds to the height of the stenosis. The maximumheight of the stenosis in case of non-tapered artery is calculated to be located at2.2 Governing equationsThe conservation equations which govern the couple stress fluid flow are
Here, represents the velocity vector,fluid density is denoted by ρ,and P corresponds to thefluid pressure. l and f denote body couple and body force,respectively. The material constantsλ and η are the dimensions of viscosity and momentum,respectively. The following inequalitiesgiven byare satisfied by the material constants λ,η,μ,and η′,respectively.
represents the velocity vector,fluid density is denoted by ρ,and P corresponds to thefluid pressure. l and f denote body couple and body force,respectively. The material constantsλ and η are the dimensions of viscosity and momentum,respectively. The following inequalitiesgiven byare satisfied by the material constants λ,η,μ,and η′,respectively.
As the flow is steady and incompressible,the above equations(3)-(4)in the absence of bodycouple and body force are reduced to
The couple stresses effect manifests itself from the last term of(7).
The equations are transformed from cartesian coordinate system(x,y,z)to cylindrical polarcoordinate system(r,θ,z)to take advantage of the axisymmetric nature of the flow. Here,the axis of symmetry of the stenosis is r = 0,and the velocity vector is therefore given by =(vr,0,vz),where vz and vr are the velocity components in the axial and radial directions,respectively,and are functions of r and z. The transformed equations are
=(vr,0,vz),where vz and vr are the velocity components in the axial and radial directions,respectively,and are functions of r and z. The transformed equations are
The shear and the couple stress tensors which are denoted by τrz and mrz,respectively,arise due to the consideration of couple stress fluid. For the couple stress fluid,the shear stresstensor is anti-symmetric. The expressions for shear and couple stress tensors are,respectively,given by
where the symmetric and anti-symmetric parts of τrz are expressed as

Further,krz = ωz,r,where ωz is the component of vorticity tensor,and drz =(vz,r +vr,z)/2is the rate of deformation tensor.
The non-dimensional parameters are obtained as follows:
Using the above non-dimensionalization,the dimensionless form of the geometry(1)after drop-ping the dashes is obtained as follows:where γ = L0/L1,and u0 is a typical axial velocity.By(13),(8)-(10)becomewhere ξ = r0/L1,and Re = ρu0r0/μ is the Reynolds number. The polarity of couple stress fluid whichis measured by β = r0 is the length dependent parameter and this quantity is identically zeroin the non-polar fluid theory. Under the assumption of mild stenosis and further consideringthe ratio of radius of the artery to the length of the stenosis to be very small,i.e.,ξ = r0From(18) and (19),it can be seen that the pressure variation depends only on the axial variable.Let
is the length dependent parameter and this quantity is identically zeroin the non-polar fluid theory. Under the assumption of mild stenosis and further consideringthe ratio of radius of the artery to the length of the stenosis to be very small,i.e.,ξ = r0From(18) and (19),it can be seen that the pressure variation depends only on the axial variable.Let

Then,(19)can be written as
2.3 Boundary conditionsThe non-dimensional conditions at the boundary are given bywhere u represents the velocity slip at the artery wall,σ = η′/η is the parameter associated withthe couple stress fluid. No couple stresses effects will be present if η′ = η,which is equivalentto saying that the couple stress tensor is symmetric.3 Solution processThe closed form solution of(20)is obtained aswhere I0(βr) and K0(βr)are the first and second kind modified Bessel functions of zeroth-order,respectively,and ci(z)(i = 1,2,3,4)are the constants of integration which are to be evaluatedusing the boundary conditions(21).The volumetric flow rate Q =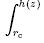 2rvzdr is obtained in the following form from(22):wherewith di(z)= ci(z)/dp/dz for i = 1,2,3,and 4.The pressure difference △P across the ends of the tube is expressed as follows:3.1 ImpedanceThe resistance to the flow(impedance)is obtained from the equationThe dimensionless form of(26)iswhere Γ = L1L .3.2 Wall shear stressThe shear stress(τrz)is calculated using the expressionwhere the symmetric and skew-symmetric parts of the stress are given byrespectively. Here,
2rvzdr is obtained in the following form from(22):wherewith di(z)= ci(z)/dp/dz for i = 1,2,3,and 4.The pressure difference △P across the ends of the tube is expressed as follows:3.1 ImpedanceThe resistance to the flow(impedance)is obtained from the equationThe dimensionless form of(26)iswhere Γ = L1L .3.2 Wall shear stressThe shear stress(τrz)is calculated using the expressionwhere the symmetric and skew-symmetric parts of the stress are given byrespectively. Here,


z = γ +/1/n1/(n−1).
Thus,the shear stress at the maximum height of the stenosis can be computed from(31)bysubstituting
r =(1 + ζz)(1 − ε).4 Results and discussion
The study of blood flow through catheterized stenosed tapered artery in the presence ofcatheter,involves the integration of various geometric and fluid variables,which influence thephysiological parameters such as the wall shear stress and the impedance(resistance to the flow).Closed form solutions are computed for the governing equations in terms of Bessel’s functions.The physiological dimensionless quantities such as the impedance and the wall shear stress inthe stenosis region and at the maximum height of the stenosis are computed numerically forvarious values of the fluid and geometric parameters using the Mathematica program. Theparameters considered are n(shape parameter),ζ(tapered parameter),rc(catheter radius),Γ(stenosis length),β(couple stress fluid parameter),σ(couple stress fluid parameter),and u(slip velocity). The obtained results are analyzed graphically. The results obtained here are ingood agreement with those reported in the literature. In general,from Figs.(3)-(16),it can beobserved that the wall shear stress and the impedance are increasing while the height of thestenosis(ε)in blood vessels is increasing. Further,in Figs.(17)-(20),where the variations ofshear stress at the wall across the entire length of the stenosis and at the maximum height of thestenosis are discussed,it is observed that shear stress along the wall is reaching the maximumat the throat of the stenosis.
Figure 3 indicates the change in impedance for various shape parameters values. It isobserved that while stenosis is growing towards symmetry,the resistance to the flow of bloodis increasing. Figure 4 shows the influence of tapered parameter on resistance to the flow. Itcan be observed from the graphical results that the obstruction to the flow is maximum for theconverging tapered artery followed by non-tapered and diverging tapered artery,respectively.The effect of the couple stress fluid parameter β on the impedance is shown in Fig. 5. Here,itcan be seen that the obstruction to the flow is decreasing as the couple stress fluid parameterβ(length dependent parameter)is increasing. Further,as β → ∞,the couple stress fluid losesits properties and behaves like a Newtonian fluid thus indicating that the resistance to the flowis larger in couple stress fluid than in a Newtonian fluid. The influence of catheter radius rc onimpedance is directly proportional as shown in Fig. 6. From the above result,we underst and that as the catheter radius increases the annular region gets narrowed,which leads to the risein the obstruction to the flow.
 |
| Fig. 3 Variation of impedance with respect ton when ζ = −0.005,β = 5,rc = 0.1,u = 0.1,δ = 0.5,and Γ = 0.5 |
 |
| Fig. 4 Variation of impedance with respect toζ when n = 5,β = 5,rc = 0.1,u =0.1,δ = 0.5,and = 0.5 |
 |
| Fig. 5 Variation of impedance with respect toβ when n = 5,ζ = −0.005,rc = 0.1,u = 0.1,δ = 0.5,and = 0.5 |
 |
| Fig. 6 Variation of impedance with respect torc when n = 5,ζ = −0.005,β = 5,u = 0.1,δ = 0.5,and = 0.5 |
Figure 7 depicts the behaviour of impedance for several values of the couple stress fluidparameter σ. Here,the impedance is decreasing while σ is increasing. It is known that thecouple stress tensor effects will be absent when σ → 1. Hence,we conclude that the couplestresses present in the fluid increase the impedance. Figure 8 helps us to underst and the effectof velocity slip on impedance. Impedance is low in case of high slip velocity; it is observedthat the slip velocity at the boundary facilitates the fluid flow. The influence of Γ(which givesthe effect of length of the stenotic region)on obstruction to the flow for various fixed taperedparameter values are shown in Figs. 9,10,and 11. The general trend that is observed in thesefigures indicates that the impedance is increasing as Γ is increasing. However,it is worth notingthat in case of converging tapered artery impedance is high for smaller values of Γ for initialfew values of ε. This behaviour is because of the fact that the radius of the tapered artery isless for higher values of Γ for ǫ ranging from 0 to 0.03(approximately). This can be understoodfrom Fig. 11.
 |
| Fig. 7 Variation of impedance with respect toδ when n = 5,ζ = −0.005,β = 5,rc = 0.1,u = 0.1,and = 0.5 |
 |
| Fig. 8 Variation of impedance with respect tou when n = 5,ζ = −0.005,β = 5,rc = 0.1,δ = 0.5,and = 0.5 |
 |
| Fig. 9 Variation of impedance with respect to when n = 5,ζ = 0,β = 5,rc = 0.1,u = 0.1,and δ = 0.5 |
 |
| Fig. 10 Variation of impedance with respectto when n = 5,ζ = 0.005,β = 5,rc = 0.1,u = 0.1,and δ = 0.5 |
 |
| Fig. 11 Variation of impedance with respectto when n = 5,ζ = −0.005,β = 5,rc = 0.1,u = 0.1,and δ = 0.5 |
The shear stress at the wall is a significant physiological parameter to be considered inthe blood flow study. Precise predictions of the distribution of the shear stress at the wall areparticularly useful in assimilating the effect of blood flow in arteries in general. The shear stressat the wall is calculated at the maximum height of the stenosis. As observed from(31),theshear stress at the wall is independent of the shape parameter. The variation of the shear stressat the wall as the tapered parameter increases is depicted in Fig. 12. Here,the shear stress atthe wall is more significant in the untapered artery compared with the tapered artery whichis diverging. Further,the converging tapered artery possesses high wall shear stress than theuntapered and tapered artery which is diverging. The effect of the length dependent parameter(β)on wall shear stress is understood from Fig. 13. It can be seen that β and shear stress atthe wall are inversely related. As explained in the case of impedance above,couple stress fluidhas more wall shear stress in comparison to that of Newtonian fluid.
 |
| Fig. 12 Variation of wall shear stress with re-spect to ζ when β = 5,rc = 0.1,u = 0.1,and δ = 0.5 |
 |
| Fig. 13 Variation of wall shear stress with re-spect to β when ζ = −0.005,rc =0.1,u = 0.1,and δ = 0.5 |
The velocity slip at the wall of the stenosed artery significantly influences the shear stressat the wall,which is noticed from Fig. 14. Here,it is observed that gain in velocity slip reducesthe shear stress at the wall. The influence of catheter radius on shear stress at the wall is shownin Fig. 15. The increasing catheter radius narrows down the lumen of the artery thus resultingin the higher values of shear stress at the wall. As couple stress fluid parameter(σ)increasesthe shear stress at the wall decreases. This behaviour is shown in Fig. 16.
 |
| Fig. 14 Variation of wall shear stress with re-spect to u when ζ = −0.005,β = 0.5,rc = 0.1,and δ = 0.5 |
 |
| Fig. 15 Variation of wall shear stress with re-spect to rc when ζ = −0.005,β = 5,u = 0.1,and δ = 0.5 |
 |
| Fig. 16 Variation of wall shear stress with re-spect to δ when ζ = −0.005,β = 5,rc = 0.1,and u = 0.1 |
In Figs. 17-18 shear stress at the wall across the entire length of the artery is studied for thesymmetric case. It is observed that the theoretical distribution of shear stress along the wallreaches a maximum at throat of the stenosis and then rapidly decreases in the diverging section.This behaviour is the same both in terms of the change in the radius of the catheter and thecouple stress fluid parameter σ whose behaviour is depicted graphically in Fig. 17 and Fig. 18 respectively. In Figs. 19-20 shear stress at the wall across the length of the stenosis has beenstudied. From Fig. 19,it can be seen the maximum shear stress is occurring at the maximumheight of the stenosis which is located at z = 1 when n = 2. Further,as anticipated the locationwhere the maximum wall shear stress occurs is shifting towards right as n increases. Further,our earlier statement which says that shear stress at the maximum height of the stenosis isindependent of shape parameter is also justified from this figure. The behaviour of the shearstress at the wall across the length of the stenosis for tapered parameter is shown in Fig. 20.Here,it is observed that the shear stress is maximum for the converging tapered artery followedby non-tapered and diverging tapered artery across the entire length of the stenosis.
 |
| Fig. 17 Variation of wall shear stress instenosis region with respect to rcwhen n = 2,ζ = 0,β = 5,u = 0.1,and δ = 0.5 |
 |
| Fig. 18 Variation of wall shear stress instenosis region with respect to δwhen n = 2,ζ = 0,β = 5,rc = 0.1,and u = 0.1 |
 |
| Fig. 19 Variation of wall shear stress instenosis region with respect to nwhen ζ = 0,β = 5,rc = 0.1,u = 0.1,and δ = 0.5 |
 |
| Fig. 20 Variation of wall shear stress instenosed region with respect to ζwhen n = 2,β = 5,rc = 0.1,u = 0.1,and δ = 0.5 |
A mathematical model has been built to discuss the flow of blood through a catheterizedasymmetric tapered stenosed artery with slip velocity at the stenosed wall. Closed form solu-tion is obtained and the effects of the various geometric and fluid parameters on physiologicalparameters such as obstruction to the flow(impedance) and shear stress at the wall are studied.The resultant observations are summarized as follows.
As the height and the stenosis length are increasing the obstruction to the flow of blood isincreasing. Converging tapered artery has more impedance and shear stress at the wall thanthe non-tapered and the diverging tapered artery. Further,diverging tapered artery has leastresistance to the flow and shear stress at the wall. The catheter is assumed to be fairly thick and hence is taken to be rigid. Further,depending upon the material properties an oscillatingthin catheter will behave similarly as that of thick catheter without oscillations. Here the in-crement in the catheter radius enhances the resistance to the flow and wall shear stress. Thewall shear stress and the impedance are decreasing while the couple stress fluid parameters σ and β are increasing. Also it is concluded that the couple stress fluid has more wall shear stress and impedance when compared to that of the Newtonian fluid.
Three different values of the velocity slip at the arterial boundary are considered,namelyu = 0.1,0.2,and 0.3,which correspond to 10%,12%,and 14% of the average velocity of theblood,respectively. The slip velocity is showing significant influence on the shear stress atthe wall and the impedance. The increase in slip reduces the shear stress at the wall and theimpedance.
| [1] | Sarkar, A. and Jayaraman, G. Nonlinear analysis of oscillatory flow in the annulus of an elastic tube: application to catheterized artery. Physics of Fluids, 13, 2901-2911 (2001) |
| [2] | Rudolf, R. and Paul, S. L. The fluid mechanics of the ureter with an inserted catheter. Journal of Fluid Mechanics, 46, 625-630 (1971) |
| [3] | Young, D. F. and Tsai, F. Y. Flow characteristics in models of arterial stenosis I,steady flow. Journal of Biomechanics, 6, 396-402 (1973) |
| [4] | Shukla, J. B., Parihar, R. S., and Rao, B. R. P. Effect of stenosis on non-Newtonian flow of the blood in an artery. Bulletin of Mathematical Biology, 42, 283-294 (1980) |
| [5] | Srinivasachary, D. and Srikanth, D. Flow of micropolar fluid through catheterized artery-a math-ematical model. International Journal of Biomathematics, 5, 1250019 (2012) |
| [6] | Mortazavinia, Z., Zare, A., and Mehdizadeh, A. Effects of renal artery stenosis on realistic model of abdominal aorta and renal arteries incorporating fluid-structure interaction and pulsatile non-Newtonian blood flow. Appl. Math. Mech. -Engl. Ed., 33, 165-176 (2012) DOI 10.1007/s10483-012-1541-6 |
| [7] | Mekheimer, Kh. S. and El Kot, M. A. The miropolar fluid model for blood flow through a stenotic arteries. International Journal of Pure and Applied Mathematics, 36, 393-405 (2007) |
| [8] | Stokes, V. K. Couple stresses in fluids. Physics of Fluids, 9, 1709-1716 (1966) |
| [9] | Srinivasachary, D. and Srikanth, D. Effect of couple stress on the flow in a constricted annulus. Archive of Applied Mechanics, 78, 251-257 (2008) |
| [10] | Srivastava, L. M. Flow of couple stress fluid through stenotic blood vessels. Journal of Biomechanics, 18, 479-485 (1985) |
| [11] | Srikanth, D. Steady polar fluid flow in a multiple constricted annulus-catheter effects. International Journal of Applied Mathematics and Mechanics, 9, 17-28 (2013) |
| [12] | Maiti, S. and Misra, J. C. Peristaltic transport of a coupe stress fluid: some applications to hemodynamics. Journal of Mechanics in Medicine and Biology, 12, 1250048 (2012) |
| [13] | Devajyoti, B. and Uday, S. C. Pulsatile blood flow through a catheterized artery with an axially non-symmetrical stenosis. Applied Mathematical Sciences, 4, 2865-2880 (2010) |
| [14] | Bijendra, S., Padma, J., and Joshi, B. K. Blood flow through an artery having radially non-symmetric mild stenosis. Applied Mathematical Sciences, 4, 1065-1072 (2010) |
| [15] | Mekheimer, Kh. S. and El Kot, M. A. The micropolar fluid model for blood flow through a tapered artery with a stenosis. Acta Mechanica Sinica, 24, 637-644 (2008) |
| [16] | Mandel, P. K. An unsteady analysis of non-Newtonian blood flow through tapered arteries with a stenosis. International Journal of Non-Linear Mechanics, 40, 151-164 (2005) |
| [17] | Brunn, P. The velocity slip of polar fluids. Rheologica Acta, 14, 1039-1054 (1975) |
| [18] | Bennett, L. Red cell slip at a wall in vitro. Science, 24, 1554-1556 (1967) |
| [19] | Misra, J. C. and Shit, G. C. Role of slip velocity in blood flow through stenosed arteries: a non-Newtonian model. Journal of Mechanics in Medicine and Biology, 7, 337-353 (2007) |
 2014, Vol. 35
2014, Vol. 35

































