Shanghai University
Article Information
- Jiang-hong YUAN, Wei-qiu CHEN, E. PAN. 2014.
- Line-integral representations for extended displacements, stresses, and interaction energy of arbitrary dislocation loops in transversely isotropic magneto-electro-elastic bimaterials
- Appl. Math. Mech. -Engl. Ed., 35(8): 1005-1028
- http://dx.doi.org/10.1007/s10483-014-1846-7
Article History
- Received Sept. 6, 2013;
- Revised Nov. 29, 2013
2. Department of Engineering Mechanics, Zhejiang University, Hangzhou 310027, P. R. China;
3. Department of Civil Engineering and Department of Applied Mathematics, University of Akron, Akron, OH 44325, U. S. A.
The magneto-electro-elastic (MEE) or multiferroic composite materials,which exhibit the multi-field couplings among the elastic,electric,and magnetic fields,have recently stimulated a great deal of scientific research for their potential applications to the multifunctional devices such as memories,harvesters,sensors,transducers,and actuators[1, 2]. MEE materials are usually composites made of multi-phases or multi-layers,such as particulate composites,rodarray composites,and laminate composites[1]. The desirable magneto-electric (ME) coupling usually arises from the strain-mediated elastic interaction across piezomagnetic-piezoelectric interfaces[1, 2]. Therefore,the interfaces can have a great influence on the property of MEE materials and the performance of MEE devices. At the same time,as common defects in crystalline solids,dislocations inevitably interact with the microstructures and interfaces of the MEE materials and therefore affect the mechanical,electrical,and magnetic properties of MEE materials. Due to the above facts,it is necessary to investigate the interaction of dislocations with interfaces in MEE composite materials.
For the problem of dislocation-interface interactions,most related work in the literature is confined to purely elastic materials[3, 4, 5, 6, 7, 8]. Little work has been done to treat the interaction of an arbitrary three-dimensional (3D) dislocation loop with the interface/surface of MEE composite materials. Recently,Han et al.[9] derived analytical expressions of the extended displacements and extended stresses induced by a planar dislocation loop of arbitrary shape in a generally anisotropic MEE bimaterial. As an extension to our recent work[3],by utilizing the potential theory,in this paper we mainly solve the extended displacements and extended stresses due to a 3D dislocation loop of arbitrary shape,and the interaction energy between two arbitrarily shaped 3D dislocation loops in transversely isotropic MEE bimaterials. The MEE bimaterial considered here is composed of two dissimilar semi-infinite transversely isotropic MEE solids, which are perfectly bonded together at a planar interface. We assume that the bimaterial interface is parallel to the isotropic plane of both MEE solids (i.e.,perpendicular to the poling direction of both MEE solids).
The present paper is organized as follows. In Section 2,we express the point-force Green’s function for the non-degenerate transversely isotropicMEE bimaterials in a new way for the sake of later derivations of the dislocation solutions. In Section 3,using Green’s function method, we derive line-integral expressions for the extended displacements and extended stresses of an arbitrary 3D dislocation loop,and the interaction energy between two arbitrary 3D dislocation loops in transversely isotropic MEE bimaterials. In Section 4,we provide several numerical examples to show the multi-field coupling effect and the influence of material interface/surface on the extended displacements,extended stresses,and interaction energy of dislocation loops. Concluding remarks are drawn in Section 5. 2 Point-force Green’s function for transversely isotropic MEE bimaterials
Before the discussion,it would be pointed out that throughout the paper we follow the conventions below: (i) The range of Roman indices is from 1 to 3 for lowercase letters (i,j,k, etc.) and from 1 to 5 for uppercase letters (I,J,K,etc.),and the range of Greek indices (α,β, γ,etc.) is from 1 to 2,unless otherwise specified. (ii) When dealing with bimaterials,the Greek index λ or μ in the square bracket (i.e.,[λ] or [μ]) indicates the corresponding relationship with material λ or material μ.
In the Cartesian coordinates (x1,x2,x3),we consider a bimaterial which is composed of two joined half-spaces,as shown in Fig. 1(a). In this bimaterial,one half-space (x3 >0) is occupied by transversely isotropic MEE material 1,and the other half-space (x3 <0) is occupied by transversely isotropic MEE material 2. The two half-spaces are perfectly bonded together at the planar interface (x3=0),which means that both the extended displacements uI and the extended stresses σ3J are continuous at x3=0 (the extended displacement and extended stress are defined in (A2)). We further assume that the isotropic plane of each material is parallel to the bimaterial interface (x3=0).
 |
| Fig. 1. Two transversely isotropic MEE half-spaces perfectly bonded together at planar interface x3=0 and arbitrarily shaped 3D dislocation loop located in one half-space of transversely isotropic MEE bimaterial (“T.I.” is abbreviation for “transversely isotropic”) |
We denote the point-force Green’s function for transversely isotropic MEE bimaterials as
 (y; x),which means the Ith component of the extended displacement at point y (y1,y2,
y3) in material λ due to the Jth component (of unit magnitude) of the extended body force
applied at point x (x1,x2,x3) in material μ (the extended body force is defined in (A2)). By
virtue of the image method,the point-force Green’s function for bimaterials can be divided into
two parts as follows:
(y; x),which means the Ith component of the extended displacement at point y (y1,y2,
y3) in material λ due to the Jth component (of unit magnitude) of the extended body force
applied at point x (x1,x2,x3) in material μ (the extended body force is defined in (A2)). By
virtue of the image method,the point-force Green’s function for bimaterials can be divided into
two parts as follows:
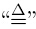 ” means that,without confusion,ψ* [μ] (y; x) and ψ* [λ][μ] (y; x) can be written as
ψ* [μ] and ψ* [λ][μ] for short,respectively. From (8b),we can further obtain the following useful
relations:
For the bimaterial with a perfectly-bonded interface,the unknown coefficients in (8a) and
(8b) are determined by[11]
and
in which the material constants sJ [μ] ,αnj [μ] ,ωnj [μ],and θnj [μ] (n = 1,2,3,4) are defined in (A6) and
(A11),respectively.
” means that,without confusion,ψ* [μ] (y; x) and ψ* [λ][μ] (y; x) can be written as
ψ* [μ] and ψ* [λ][μ] for short,respectively. From (8b),we can further obtain the following useful
relations:
For the bimaterial with a perfectly-bonded interface,the unknown coefficients in (8a) and
(8b) are determined by[11]
and
in which the material constants sJ [μ] ,αnj [μ] ,ωnj [μ],and θnj [μ] (n = 1,2,3,4) are defined in (A6) and
(A11),respectively.
Also in (8a) and (8b),the unknown functions are defined as[13, 14]
or where The functions defined in (12) satisfy the following useful relations: and 3 Line-integral forms of extended displacements,stresses,and interac- tion energy of arbitrarily shaped 3D dislocation loops in transversely isotropic MEE bimaterials 3.1 Extended displacements of arbitrarily shaped 3D dislocation loopNow,we consider an arbitrarily shaped 3D dislocation loop C bounding a curved surface A in transversely isotropic MEE bimaterials (see Fig. 1(b)). Based upon the classical theory of dislocations,the extended displacements induced by this dislocation loop can be expressed as[15]
where uN [μ][λ] (x) is the Nth component of the extended displacement at point x (x1,x2,x3) in material μ due to the dislocation loop C located in material λ,dAi at point y (y1,y2, y3) is the ith component of the vector area element dA,and the positive normal of dA is associated with the positive direction of the closed dislocation line according to the right-hand rule (Fig. 1(b)),the extended elastic coefficient tensor ciJKl [λ] is defined by (A3a) and (A3b),bJ is the Jth component of the extended Burgers vector b defined as in which uJ - and uJ + denote the Jth component of the extended displacement at the same point on the lower and upper surface of the cut face,respectively. The positive normal of dA (see Fig. 1(b)) should point from the lower surface to the upper surface of the cut face. In this paper, we assume that the extended Burgers vector b is constant over the dislocation surface.Substituting (1) into (17),we can obtain that
where The above uN [λ] (x) denotes the Nth component of the extended displacement at point x (x1, x2,x3) induced by the dislocation loop C in a transversely isotropic MEE full space occupied by material λ,and UN [μ][λ] (x) is the complementary part from the image sources due to the bimaterial interface.Substituting (A3a),(A3b),(4),(5a),and (5b) into (20),and then making use of (15),(16), (A6),(A13),and the following Stokes’ theorem[16]
or we can transform the area integrals in (20) into the line-integral form as follows: where ℓ[μ] [λ] = c44 [λ] /c44 [μ] , in which the material constants Cij [λ] and CJ [λ] are defined in (A12a) and (A12b),respectively. It can be observed from (23c) and (23d) that Note that the area integral Ω 5 [λ] (x) in (23a) denotes the quasi solid angle subtended by the cut face A of the dislocation loop C in material λ at point x,which can also be transformed into a line integral[17]. 3.2 Extended stresses of arbitrarily shaped 3D dislocation loopUsing the constitutive relation for transversely isotropic MEE materials as shown in (A1b), we can derive from (19) the extended stresses as follows:
in which where σiJ [μ][λ] (x) denotes the extended stress at point x (x1,x2,x3) in transversely isotropic MEE material μ due to an arbitrarily shaped 3D dislocation loop C located in transversely isotropic MEE material λ,σiJ [λ] (x) is the extended stresses at point x (x1,x2,x3) induced by the same dislocation loop C in a transversely isotropic MEE full space occupied by material λ, SiJ [μ][λ] (x) is the complementary part from the image sources due to the bimaterial interface.Substituting (22) into (26),we can express σiJ [λ] (x) and SiJ [μ][λ] (x) in terms of line integrals
whereDuring the derivation of (27),we have made use of (15) and (16),along with the following relations:
and (30) can be verified by Stokes’ theorem in (21).By virtue of (9),we can obtain from (28b) and (28c) that
and 3.3 Interaction energy between two arbitrarily shaped 3D dislocation loops
Suppose that there are two arbitrarily shaped 3D dislocation loops C and 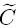 in transversely
isotropic MEE bimaterials. The dislocation loop C is located in material λ and bounds a curved
surface A with an extended Burgers vector b,the dislocation loop
in transversely
isotropic MEE bimaterials. The dislocation loop C is located in material λ and bounds a curved
surface A with an extended Burgers vector b,the dislocation loop 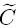 is located in material μ
and bounds a curved surface
is located in material μ
and bounds a curved surface  with an extended Burgers vector
with an extended Burgers vector  . Based upon the classical
theory of dislocations[15],the interaction energy wI [μ][λ] between the two dislocation loops can
be expressed as
. Based upon the classical
theory of dislocations[15],the interaction energy wI [μ][λ] between the two dislocation loops can
be expressed as
 p is the pth component of the vector area element d
p is the pth component of the vector area element d defined at point
x (x1,x2,x3) on the dislocation surface
defined at point
x (x1,x2,x3) on the dislocation surface  . The above wI [λ] is the interaction energy between the
two dislocation loops
. The above wI [λ] is the interaction energy between the
two dislocation loops 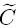 and C in a transversely isotropic MEE full space occupied by material
λ,and WI [μ][λ] is the complementary part from the image sources due to the bimaterial interface.
and C in a transversely isotropic MEE full space occupied by material
λ,and WI [μ][λ] is the complementary part from the image sources due to the bimaterial interface.
Substituting (27) into (33),and then making use of (16),the Stokes theorem in (21) and the following relations:
we can thus express the interaction energy in terms of double line integrals as in which and As an immediate application of (36),we now consider one dislocation loop C with an extended Burgers vector (b1,b2,b3,0,0) and another dislocation loop ˜ C with an extended Burgers vector ( 1,
1, 2,
2, 3,0,0),both of which are located in the transversely isotropic MEE full space
occupied by material λ. In this special case,the interaction energy between the two dislocation
loops can be expressed in an elegant way as
in which
During the derivation of (38) from (36),we have made use of (16) and (34),along with the
following relations:
and
(40) can be verified by Stokes’ theorem in (21).
3,0,0),both of which are located in the transversely isotropic MEE full space
occupied by material λ. In this special case,the interaction energy between the two dislocation
loops can be expressed in an elegant way as
in which
During the derivation of (38) from (36),we have made use of (16) and (34),along with the
following relations:
and
(40) can be verified by Stokes’ theorem in (21).
Now,we consider a single dislocation loop C with an extended Burgers vector b,which bounds a curved surface A in material λ of the transversely isotropicMEE bimaterial. According to Hirth and Lothe[15],we can express the self-energy wS [λ] of the dislocation loop C as
where in which σpQ [λ](x) and SpQ[μ][λ](x) are the two parts of the extended stress induced by the dislocation loop C,as given in (27); dAp is the pth component of the vector area element dA defined at point x (x1,x2,x3) on the dislocation surface A. The above wFS[λ] is the self-energy of the dislocation loop C in a transversely isotropic MEE full space occupied by material λ,and WIS[λ] is the image self-energy from the image sources due to the bimaterial interface.Following the derivation of (36),similarly,we can obtain from (43) that
and In summary,we have presented line-integral expressions for the extended displacements, extended stresses,interaction energy,and self-energy of arbitrarily shaped 3D dislocation loops in transversely isotropic MEE bimaterials,as shown in (22),(27),(36),(44a),and (44b). These line-integral expressions are the main results of this paper. 4 Numerical examples and discussionIn this section,we utilize our dislocation solutions in Section 3 to investigate the multi-field coupling effect and the interface/surface effect in transversely isotropic MEE materials. Before presenting the numerical examples,we point out that our formulations have been verified to be correct by comparing our numerical results with those in Han and Pan[18].
Example 1 The extended displacements and extended stresses of a cardioid dislocation loop in transversely isotropic MEE bimaterials.
In the Cartesian coordinates,we consider a transversely isotropic bimaterial which is composed of the MEE BaTiO3-CoFe2O4 (material 1,x3 > 0) and the piezoelectric BaTiO3 (material 2,x3 < 0),with the isotropic plane of both materials being parallel to the perfectly bonded interface (i.e.,x3=0). The MEE BaTiO3-CoFe2O4 composite is based on the 25% BaTiO3 and 75% CoFe2O4. The material coefficients used here are listed as follows[9]:
We consider a cardioid dislocation loop C1 whose parametric equation is described by
with h being a real constant and a being the shape parameter of the cardioid (see Fig. 2). In this example,the cardioid dislocation loop is assumed to be located on the plane x3 = h = 0.5a in material 1 (i.e.,MEE BaTiO3-CoFe2O4). |
| Fig. 2. Schematic of cardioid dislocation loop C1 described by (45) |
Shown in Figs. 3 and 4 are the electric potential φ,magnetic potential ψ,electric displacement component D3,and magnetic induction component B3 on a vertical line (i.e.,x1 = 0,x2 = 0.5a,−4a 6 x3 6 5a) due to the loop C1 with an extended Burgers vector (0,0,0,Δφ1, 0) or (0,0,0,0,Δψ1). Three different cases are investigated,in which the loop C1 is located in the perfectly-bonded MEE bimaterial as mentioned above,an MEE BaTiO3-CoFe2O4 half space (x3 ≥ 0) with a free surface at x3 = 0 (see Appendix B),and MEE BaTiO3-CoFe2O4 full space. It can be observed from Figs. 3 and 4 that the curves are very sensitive to different boundary conditions except for those in Figs. 3(d) and 4(d). This is mainly caused by the fact that BaTiO3 (i.e.,material 2) has relatively large dielectric and piezoelectric coefficients while but extremely small piezomagnetic and magnetic-permeability coefficients. In addition, Figs. 3(b),3(c),4(b),and (4c) show an obvious ME coupling effect in MEE materials.
 |
| Fig. 3. Electric potential φ or magnetic potential ψ on vertical line (i.e.,x1 = 0,x2 = 0.5a,−4a ≤ x3 ≤ 5a) due to the cardioid loop C1 with extended Burgers vector (0,0,0,Δφ1,0) or (0,0, 0,0,ΔΨ1): (a) φ ~ (0,0,0,Δφ1,0); (b) Ψ ~ (0,0,0,Δφ1,0); (c) φ ~ (0,0,0,0,ΔΨ1); (d) Ψ~ (0,0,0,0,ΔΨ1) |
 |
| Fig. 4. Electric displacement component D3 or magnetic induction component B3 on vertical line (i.e.,x1 = 0,x2 = 0.5a,−4a ≤ x3 ≤ 5a) due to the cardioid loop C1 with extended Burgers vector (0,0,0,Δφ1,0) or (0,0, 0,0,ΔΨ1): (a) D3 ~ (0,0,0,Δφ1,0); (b)B3 ~ (0,0,0,Δφ1,0); (c) D3 ~ (0,0,0,0,ΔΨ1); (d)B3 ~ (0,0,0,0,ΔΨ1) |
Example 2 The interaction energy between two cardioid dislocation loops in transversely isotropic MEE bimaterials
In this example,we investigate the influence of the bimaterial interface and the half-space surface on the interaction energy between two cardioid dislocation loops C1 and C2 in MEE materials. The models of the MEE bimaterial,half space (x3 ≥ 0) and full space are exactly the same as those in Example 1. The first loop C1 with the extended Burgers vector (0,0,0, Δφ1,0) or (0,0,0,0,Δψ1) is also described by (45) with h = 0.5a. The second loop C2 with the extended Burgers vector (0,0,0,Δφ2,0) or (0,0,0,0,Δψ2) is described by the following parametric equation:
with X3 being independent of the parameter t. It is noted that (46) is just a simple translation relative to (45).The numerical results for the interaction energy between loops C1 and C2 are shown in Fig. 5. Similarly to Figs. 3 and 4 in Example 1,the interaction energy in Fig. 5 is also sensitive to different boundary conditions,and an obvious ME coupling effect is also observed.
 |
| Fig. 5. Influence of location of loop C2 (i.e.,X3) on interaction energy wI between loop C1 described by (45) with extended Burgers vector (0,0,0,Δφ1,0) or (0,0,0,0,ΔΨ1) and loop C2 described by (46) with extended Burgers vector (0,0,0,Δφ2,0) or (0,0,0,0,ΔΨ2): (a) wI ~ (0,0,0,Δφ1,0) and (0,0,0,Δφ2,0); (b) wI ~ (0,0,0,Δφ1,0) and (0,0,0,0,ΔΨ2); (c) wI ~ (0,0,0,0,ΔΨ 1) and (0,0,0,Δφ2,0); (d) wI ~ (0,0,0,0,ΔΨ1) and (0,0,0,0,ΔΨ2) |
Example 3 The image self-energy of a cardioid dislocation loop in transversely isotropic MEE bimaterials.
In this example,the model of the MEE bimaterial is also exactly the same as in Example 1. An MEE BaTiO3-CoFe2O4 half space (x3 ≥ 0) and a piezoelectric BaTiO3 half space (x3≤6 0), both with a free surface at x3 = 0,are also considered here.
We first investigate the influence of the distance between the interface/surface and the cardioid dislocation loop C2 on its image self-energy. Here,the cardioid loop C2 is also described by (46),with its extended Burgers vector being (0,0,0,Δφ2,0) or (0,0,0,0,Δψ2). The numerical results are shown in Fig. 6. It can be observed from Fig. 6 that (i) for the loop C2 with an extended Burgers vector (0,0,0,Δφ2,0),the perfect bimaterial interface imposes an attractive force upon this loop if it is located within MEE BaTiO3-CoFe2O4 which exhibits a relatively weaker piezoelectric effect,and imposes a repulsive force upon this loop if it is located within BaTiO3 which exhibits a relatively stronger piezoelectric effect; (ii) for the loop C2 with an extended Burgers vector (0,0,0,0,Δψ2),the perfect bimaterial interface imposes a repulsive force upon this loop if it is located within MEE BaTiO3-CoFe2O4 which exhibits a relatively stronger piezomagnetic effect,and imposes an attractive force upon this loop if it is located within BaTiO3 which exhibits a relatively weaker piezomagnetic effect; (iii) for the loop C2 with an extended Burgers vector either (0,0,0,Δφ2,0) or (0,0,0,0,Δψ2),the free surface always imposes a repulsive force upon this loop. In other words,if the interface or surface is present,the dislocation loop with an electric-potential (or a magnetic-potential) discontinuity always has the tendency to move towards the material with a relatively stronger piezoelectric (or piezomagnetic) effect. This phenomenon in MEE materials is quite different from that for dislocation loops in purely elastic materials[3].
 |
| Fig. 6.Influence of location of loop C2 (i.e.,X3) on image self-energy WIS of loop C2 described by (46) with extended Burgers vector (0,0,0,Δφ2,0) or (0,0,0,0,ΔΨ2): (a) WIS ~ (0,0,0, Δφ2,0); (b) WIS ~ (0,0,0,0,ΔΨ2) (“PE” is abbreviation for “piezoelectric”) |
Then,we investigate the influence of the size of the cardioid dislocation loop C1 on its image self-energy. Here,the cardioid loop C1 with an extended Burgers vector (0,0,0,Δφ1, 0) or (0,0,0,0,Δψ1) is also described by (45) with h = 0.5a0 or −0.5a0 (a0 = const. > 0), but we change the size of this cardioid loop by simply changing its shape parameter a. The numerical results are shown in Fig. 7. It can be observed from Fig. 7 that (i) for the loop C1 with an extended Burgers vector (0,0,0,Δφ1,0),the perfect bimaterial interface imposes an expanding force upon this loop if it is located within MEE BaTiO3-CoFe2O4 which exhibits a relatively weaker piezoelectric effect,and imposes a shrinking force upon this loop if it is located within BaTiO3 which exhibits a relatively stronger piezoelectric effect; (ii) for the loop C1 with an extended Burgers vector (0,0,0,0,Δψ1),the perfect bimaterial interface imposes a shrinking force upon this loop if it is located within MEE BaTiO3-CoFe2O4 which exhibits a relatively stronger piezomagnetic effect,and imposes an expanding force upon this loop if it is located within BaTiO3 which exhibits a relatively weaker piezomagnetic effect; (iii) for the loop C1 with an extended Burgers vector either (0,0,0,Δφ1,0) or (0,0,0,0,Δψ1),the free surface always imposes a shrinking force upon this loop.
 |
| Fig. 7.Influence of size of loop C1 on image self-energy of loop C1 described by (45) with extended Burgers vector (0,0,0,Δφ1,0) or (0,0,0,0,ΔΨ1): (a) WIS ~ (0,0,0,Δφ1,0); (b) WIS ~ (0,0,0,0,ΔΨ1) (“PE” is abbreviation for “piezoelectric”) |
In this paper,we derive simple and elegant line-integral expressions for the extended displacements, extended stresses,interaction energy,and self-energy of arbitrarily shaped 3D dislocation loops with constant extended Burgers vector in transversely isotropic MEE bimaterials. These expressions are very similar to their elastic isotropic full-space counterparts,such as Burgers’ formula for displacements[19],Peach-Koehler’s formula for stresses[20],and Blin’s formula for the interaction energy[21]. Moreover,it is straightforward to reduce our line-integral expressions for MEE materials to those for piezoelectric,piezomagnetic,or purely elastic materials.
Our line-integral expressions for transversely isotropic MEE bimaterials are also suitable for a transversely isotropic MEE half space,provided that we slightly modify some coefficients of the point-force Green’s function for bimaterials,as shown in Appendix B.
All possible degenerate cases of these expressions can be treated systematically via proper limiting processes[3]. In numerical calculations,we can also deal with these degenerate cases by means of a slight perturbation to material coefficients.
Our numerical examples show clearly the multi-field coupling and interface/surface effects on the extended displacements,extended stresses,and interaction energy of dislocation loops in the MEE materials. It is also observed from Example 3 that,for a dislocation loop with an electric-potential (or a magnetic-potential) discontinuity,the bimaterial interface would impose repulsive and shrinking forces to the dislocation loop embedded in the MEE material with a relatively stronger piezoelectric (or piezomagnetic) effect,while it would impose attractive and expanding forces to the dislocation loop embedded in the MEE material with a relatively weaker piezoelectric (or piezomagnetic) effect; however,the half-space surface would always impose repulsive and shrinking forces to the dislocation loop.
Acknowledgements The first author would like to dedicate this paper to the late Professor Y. H. PAO from College of Civil Engineering and Architecture in Zhejiang University for his supervision. Appendix A General solutions of coupled equations for transversely isotropic MEE mediaUsing the extended Barnett and Lothe notation[22, 23],in Cartesian coordinates (x1,x2,x3),the governing equations and constitutive relations for transversely isotropic MEE media can be expressed as
in which the extended body force,extended displacement,and extended stress are defined as where fi,fe,and fm are the body force,electric charge,and electric current (or called magnetic charge), respectively; ui,φ,and Ψ are the elastic displacement,electric potential,and magnetic potential, respectively; σij ,Di,and Bi are the stress,electric displacement,and magnetic induction,respectively.Also in (A1a) and (A1b),the extended elastic coefficient tensor for transversely isotropic MEE media can be written as
where cijkl,εij ,and μij are the elastic,dielectric,and magnetic permeability coefficients,respectively; eijk,qijk,and dij are the piezoelectric,piezomagnetic,and magnetoelectric coefficients,respectively. If the isotropic plane of the transversely isotropic MEE medium is parallel to the x1x2-plane,then the above coefficients can be expressed explicitly as where cmn,ein,and qin (m,n=1,2,3,4,5,6) are the contracted elastic,piezoelectric,and piezomagnetic coefficients; δij is the 3×3 Kronecker delta.According to Hou et al.[11] and Chen et al.[12] ,the general solution of (A1a) and (A1b) can be expressed compactly as
and where i =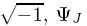 satisfies the quasi-harmonic equations as follows:
with
In (A4b),(A5),and (A6),
Υn (n=1,2,3,4) satisfies the following characteristic equation:
where
In other words,Υn (n=1,2,3,4) are the four roots (with positive real part) of the following algebraic
equation:
where
satisfies the quasi-harmonic equations as follows:
with
In (A4b),(A5),and (A6),
Υn (n=1,2,3,4) satisfies the following characteristic equation:
where
In other words,Υn (n=1,2,3,4) are the four roots (with positive real part) of the following algebraic
equation:
where
Other coefficients in (A4a) and (A4b) are defined as
where Λn;pq (n,p,q = 1,2,3,4) are the cofactors of the pq element of the matrix Πn defined by (A8); Cij is the element of a symmetric matrix defined by and CJ is defined by Obviously,we have C1j = Cj1 = Cj+2.Notice that mnj (n=1,2,3,4) satisfy the following relation:
in which “T” denotes the transpose of a matrix or a vector.Moreover,we have the following relations:
which can be verified by direct substitutions. In (A14),Hn (n = 1,2,3,4) are given by (10). Appendix B Dislocation loops in transversely isotropic MEE half space with free surfaceFor arbitrarily shaped 3D dislocation loops in a transversely isotropic MEE half space with a free surface,the line-integral expressions given in (22),(27),(36),(44a),and (44b) are still applicable,pro- vided that we make modifications to (11a) and (11b) according to the free-surface boundary condition, and then set λ = μ=1 for the half space x3 ≥0 while λ = μ = 2 for the half space x3 ≤0. Here,we also assume that the isotropic plane of the transversely isotropic material is parallel to the free surface of the half space (i.e.,the x1x2-plane).
The free-surface boundary condition means the vanishing of the extended stresses σ3J at x3 = 0, which gives,corresponding to (11a) and (11b),that
and| [1] | Nan, C. W., Bichurin, M. I., Dong, S. X., Viehland, D., and Srinivasan, G. Multiferroic mag-netoelectric composites: historical perspective, status, and future directions. Journal of Applied Physics, 103, 031101 (2008) |
| [2] | Ma, J., Hu, J. M., Li, Z., and Nan, C. W. Recent progress in multiferroic magnetoelectric com-posites: from bulk to thin films. Advanced Materials, 23, 1062-1087 (2011) |
| [3] | Yuan, J. H., Pan, E., and Chen, W. Q. Line-integral representations for the elastic displacements, stresses and interaction energy of arbitrary dislocation loops in transversely isotropic bimaterials. International Journal of Solids and Structures, 50, 3472-3489 (2013) |
| [4] | Chu, H. J., Pan, E., Han, X., Wang, J., and Beyerlein, I. J. Elastic fields of dislocation loops in three-dimensional anisotropic bimaterials. Journal of the Mechanics and Physics of Solids, 60, 418-431 (2012) |
| [5] | Chu, H. J., Pan, E., Wang, J., and Beyerlein, I. J. Elastic displacement and stress fields induced by a dislocation of polygonal shape in an anisotropic elastic half-space. Journal of Applied Mechanics, 79, 1-9 (2012) |
| [6] | Akarapu, S. and Zbib, H. M. Line-integral solution for the stress and displacement fields of an arbitrary dislocation segment in isotropic bi-materials in 3D space. Philosophical Magazine, 89, 2149-2166 (2009) |
| [7] | Tan, E. H. and Sun, L. Z. Stress field due to a dislocation loop in a heterogeneous thin film-substrate system. Modelling and Simulation in Materials Science and Engineering, 14, 993-1013 (2006) |
| [8] | Gosling, T. J. and Willis, J. R. A line-integral representation for the stresses due to an arbitrary dislocation in an isotropic half-space. Journal of the Mechanics and Physics of Solids, 42, 1199-1221 (1994) |
| [9] | Han, X. L., Pan, E., and Sangghaleh, A. Fields induced by three-dimensional dislocation loops in anisotropic magneto-electro-elastic bimaterials. Philosophical Magazine, 93, 3291-3313 (2013) |
| [10] | Chen, W. Q., Pan, E., Wang, H. M., and Zhang, C. Z. Theory of indentation on multiferroic composite materials. Journal of the Mechanics and Physics of Solids, 58, 1524-1551 (2010) |
| [11] | Hou, P. F., Ding, H. J., and Chen, J. Y. Green's functions for transversely isotropic magnetoelec-troelastic media. International Journal of Engineering Science, 43, 826-858 (2005) |
| [12] | Chen, W. Q., Lee, K. Y., and Ding, H. J. General solution for transversely isotropic magneto-electro-thermo-elasticity and the potential theory method. International Journal of Engineering Science, 42, 1361-1379 (2004) |
| [13] | Ding, H. J., Chen,W. Q., and Zhang, L. C. Elasticity of Transversely Isotropic Materials, Springer, New York (2006) |
| [14] | Fabrikant, V. I. A new form of the Green function for a transversely isotropic body. Acta Mechan-ica, 167, 101-111 (2004) |
| [15] | Hirth, J. P. and Lothe, J. Theory of Dislocations, John Wiley & Sons, New York (1982) |
| [16] | Mura, T. Micromechanics of Defects in Solids, Martinus-Nijhoff Publishers, Dordrecht (1987) |
| [17] | Yuan, J. H., Chen, W. Q., and Pan, E. Line-integral representations of the displacement and stress fields due to an arbitrary Volterra dislocation loop in a transversely isotropic elastic full space. International Journal of Solids and Structures, 50, 160-175 (2013) |
| [18] | Han, X. L. and Pan, E. Fields produced by three-dimensional dislocation loops in anisotropic magneto-electro-elastic materials. Mechanics of Materials, 59, 110-125 (2013) |
| [19] | Burgers, J. M. Some considerations on the fields of stress connected with dislocations in a regular crystal lattice. Koninklijke Nederlandse Akademie van Wetenschappen, 42, 293-325 (1939) |
| [20] | Peach, M. and Koehler J. S. The forces exerted on dislocations and the stress fields produced by them. Physical Review, 80, 436-439 (1950) |
| [21] | Blin, J. Energie mutuelle de deux dislocations. Acta Metallurgica, 3, 199-200 (1955) |
| [22] | Barnett, D. M. and Lothe, J. Dislocations and line charges in anisotropic piezoelectric insulators. Physica Status Solidi, 67b, 105-111 (1975) |
| [23] | Pan, E. Three-dimensional Green's functions in anisotropic magneto-electro-elastic bimaterials. Zeitschrift für Angewandte Mathematik und Physik, 53, 815-838 (2002) |
 2014, Vol. 35
2014, Vol. 35























































































