Shanghai University
Article Information
- Fang GAO, Xiao-bo ZHANG, Jing-li FU. 2014.
- Application of canonical coordinates for solving single-freedom constraint mechanical systems
- Appl. Math. Mech. -Engl. Ed., 35(8): 1029-1038
- http://dx.doi.org/10.1007/s10483-014-1849-7
Article History
- Received Nov. 29, 2013;
- Revised Feb. 21, 2014
The symmetric theory has been widely used in mathematics,physics,mechanics,and dynamical systems. In early years,Lie group theory method has been a popular and useful method in the study of ordinary differential equations (ODEs) and partial differential equations (PDEs)[ 1, 2, 3, 4, 5, 6 ]. Bluman[ 1 ] and Olver[ 2, 3 ] have showed that one can use canonical coordinates or differentials invariant’s method to reduce the order or to solve the differential equation with Lie group. In other words,given ODEs or PDEs with known Lie symmetries,one can obtain the corresponding canonical coordinates or differentials invariants,and then get the equations after reduction of order. Furthermore,the solutions of the equations can be obtained.
In the late 20th century,Noether symmetry and Lie symmetry were widely introduced to solve the problems of constraint mechanical system[ 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28 ]. Noether,the famous German mathematician, established the Noether theorem that can be described as that each successive symmetry of the mechanical system action has the corresponding conserved quantity. The Noether symmetry is that the Hamilton action is an invariant under infinitesimal transformations of group in phase space. Calculating the killing equations,we can obtain the infinitesimal transformations which can be substituted to the Noether theorem to get the Noether conserved quantities. In addition,the basic idea of Lie symmetry is to keep the equation of motion invariant under the infinitesimal transformations. We can obtain generational functions and normal functions from determining equations and structural equations. Then,the conserved quantities can be obtained from Lie theorem with the infinitesimal transformation and structural equations. Nowadays,many good and useful results have been obtained using the symmetric theory to constrained mechanical system in the papers by Feng-xiang MEI et al.
The main point of using the canonical coordinates method to constraint mechanical system is that the corresponding canonical coordinates can be calculated with the infinitesimal transformations which can be obtained through determining equations,and then the first integrals of the equation of motion can be derived. In recent years,canonical coordinates method has been widely used to solve many problems in many fields[ 29, 30, 31, 32, 33, 34, 35, 36, 37 ]. However,applying canonical coordinates method to dynamic system and obtaining the corresponding first integral have not been studied. In the paper,this problem will be solved. 2 Canonical coordinates
In this section,we review the definition and properties of the canonical coordinates which have been given in Ref. [ 1 ],where some good results have been established about canonical coordinates. Now,let us consider a one-parameter Lie group transformation
in which x = (x1,x2,· · · ,xn) are variables,ξ(x) = ∂X/∂ε(x;ε) and X =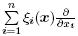 are
infinitesimal and infinitesimal generator of (1). Let us introduce the coordinate transformation,
Thus,the corresponding infinitesimal generators become Y =
are
infinitesimal and infinitesimal generator of (1). Let us introduce the coordinate transformation,
Thus,the corresponding infinitesimal generators become Y =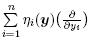 .
.
Definition 1 The change of coordinates (2) defines a set of canonical coordinates for the one-parameter Lie group of transformations (1). Then,the group (1) turns into
Theorem 1 Assume that the canonical coordinates of equation are (s(x,y),r(x,y)),non- trivial one-parameter Lie group of transformations should satisfy
where infinitesimal generators are X = ξ(x,y)∂/∂x +η(x,y)∂/∂y . Then,solving the nth-order ODE yn = f(x,y,y′,· · · ,yn-1) reduces to solving the (n − 1)th-order one where z = ds/dt ,and the nontrivial one-parameter Lie group transformations areTheorem 2 If z = φ(r;C1,C2,· · · ,Cn−1) is the general solution of (5),then the general solution of ODE is
where C1,C2,· · · ,Cn are constants. 3 Lie point symmetry of constraint homonomic systemIn this part,Lie group theory is used to determine Lie point symmetries of the motion of equation of the single-freedom constraint homonomic system. The system is non-singular and can be described by the Euler-Lagrange equation in the form as
Case 1 If Q(t,q,q˙) = 0,the system is a conservative homonomic system,the equation of motion can be expressed in the form as
Case 2 If Q(t,q,q˙) 6= 0,the system is a non-conservative homonomic system. After decoupling, the equation of motion still has the same form as (9).
We assume that the system has one-parameter Lie point symmetry. Thus,the infinitesimal transformations with respect to time and generalized coordinates can be introduced as follows:
where ε is a parameter,and ξ and η are infinitesimals. The group is determined by its infinitesimal generator, The generator of the first extended group is given by Its second extension has the form Thus,the basic idea of Lie symmetry is to keep (9) invariant under the infinitesimal transformations (10) that must satisfy the determining equation Then,we have Obviously,we can get the infinitesimal transformations from (15). 4 Canonical coordinates and first integral of conservative homonomic system Now,we discuss a homonomic system with the method of canonical coordinates. We had worked out the infinitesimal transformation (ξ(t,q),η(t,q)) with (15). Then,using (4) and (11), we obtain (r,s) = (f(t,q),g(t,q)). Finally,the derivations of canonical coordinates are given by If sqrt − strq 6≠ 0,we have Then,we can obtain q˙ and from (17),
Substituting (18) into (9) leads to
Canonical coordinate s is free from function ',where z = ds/dt . If (19) has the general solution,
then the general solution of (9) can be obtained. Unless,we can obtain the first integral of the
equation of the motion.
from (17),
Substituting (18) into (9) leads to
Canonical coordinate s is free from function ',where z = ds/dt . If (19) has the general solution,
then the general solution of (9) can be obtained. Unless,we can obtain the first integral of the
equation of the motion.
In this part,two different examples about conservative homonomic system are considered. The new conserved quantities have been constructed from the different canonical coordinates.
Example 1 We now consider an example of the harmonic oscillator[ 11 ],the equation of motion is
and the determining equation of the system under the infinitesimal transformation (10) is (21) is a polynomial equation of degree three in q˙. Let the coefficients of q˙n euqal to zero (n = 0, 1,2,3),we obtain a system of partial differential equations as To find the corresponding infinitesimal generators,(22) should be solved. Then,we have After some calculations,(4) and (23)-(25) yield the canonical coordinates of the system, If the canonical coordinates do not satisfy the condition of the coordinates of (26),then by use of (20) and (27)-(28),(19) can be written as where z2 = ds2/dr2 ,and z3 = ds3/dr3 . Thus,the general solutions of (26) and (27) can be given as According to Theorem 2,we have the general solutions of (20) where Ci (i = 1,2,3,4) are constants.Example 2 Now,we use the method of canonical coordinates to seek the conserved quantity of the variable mass homonomic systems[ 15 ]. The spherical raindrops are falling straight down in the atmosphere,and are supplied with water vapor. Due to condensation,the masses of the raindrops increase with a rate that is proportional to the surface area. α is a proportionality coefficient. The initial speed of the raindrops is v0.
For dm/dt = 4πv2,v = v0 + αt,we have m = 4πv3/3 . When the absolute velocity of particles into the atmosphere is zero and m only depends on t,we can get that the reaction thrust p is zero from

The Lagrangian of the system is L = 1 2mq˙2 − mgq,where q is the vertical coordinate. The equation of motion is
Then,we have the determining equation of the system under the infinitesimal transformation (10), (36) yields a set of equations that can be separated with respect to q˙. The resulting equations are The solution of (37) is Using (4) and (38),we get the canonical coordinates of the system From (16)-(17),the original equation can be rewritten in the form as Setting z = ds/dr ,one has In order to obtain the conserved quantity of the system,we should choose the canonical coordinates r appropriately. Through calculation,we get the function !(t) as follows. (i) Set !(t) = kt,where k is a nonzero arbitrary constant. (41) can be expressed as Therefore,the system possesses the conserved quantity. According to Theorem 2,we can also get the general solution of the system as follows: where c is a constant.(ii) Let !(t) = ekt,where k is a nonzero arbitrary constant. One has
Obviously,one conserved quantity of the system can be deduced from (44).(iii) Set !(t) = sin t. (41) can be expressed as
Three conserved quantities (42),(44),and (45) of the system have been found finally. We should point out that the different first integral of the system would be obtained by taking different !(t). 5 Canonical coordinates and first integral of non-conservative homonomic systemIn the section,the canonical coordinates method used to non-conservative system will be discussed. The canonical coordinates (r,s) are determined by (4) and (11). Then,we take the differential of canonical coordinates
If the basic condition sqrt − strq 6≠0 can be satisfied,we have Substituting (47) into (9) yields an ordinary differential equation The first integral of the non-conservative system has been given.Example 3 The Euler-Lagrange equation and the generalized force of the system are in the form of L = 1/2 q˙2 and Q = q˙. Thus,the equation of the motion can be written as
The determining equation of the system (49) under the infinitesimal transformation (10) is equating to zero the coefficients of powers of q˙ leads to a system of four partial differential equations, and the solution isDifferent solutions of (51) can be obtained,if parameters c1 and c2 are given different values in (52). We discuss two possibilities in the following.
(i) Set c1 = 1 and c2 = 0. The infinitesimal transformation becomes
Group (10) is completely defined by One can obtain the canonical coordinates with (4) and (54) like We can easily get From (56),we have Set z = ds/dr . Substituting (57) into (49) leads to Obviously,(48) is the first integral of the system.(ii) Set c1 = 1 and c2 = 1,then we get the infinitesimal transformation (1,q + 1),whose corresponding generator is
The derivation of canonical coordinates can be written as where canonical coordinates are (r,s) = (e−t(q + 1),t). For sqrt − strq 6≠ 0,q˙ and q¨ can be written in the forms of Set z = ds/dr . Substituting (61) into (49) leads toObviously,the system has the conserved quantity (62) and the general solution as s = cer, where c is a constant. 6 Conclusions
In this paper,the first integral of the homonomic system with the canonical coordinates method has been obtained. The method to construct canonical coordinates for the equations of motion in multi-degree of freedom for a constraint system remains to be studied.
| [1] | Bluman, G. W. and Kumei, S. Symmetries and Differential Equations, Springer, Berlin (1989) |
| [2] | Olver, P. J. Applications of Lie Groups to Differential Equations, Springer, Berlin (2000) |
| [3] | Olver, P. J. Equivalence, Invariants and Symmetry, Cambridge University Press, Cambridge (1995) |
| [4] | MacCallum, M. Differential Equations: Their Solution Using Symmetries, Cambridge University Press, Cambridge (1989) |
| [5] | Ovsiannikov, L. V. Group Analysis of Differential Equations, Academic Press, New York (1982) |
| [6] | Gorringe, V. M. and Leach, P. G. L. Lie point symmetries for systems of second order linear ordinary differential equations. Quaestiones Mathematicae, 11(1), 95-117 (1988) |
| [7] | Noether, E. Invariante variations probleme. Transport Theory and Statistical Physics, 1(3), 186-207 (1971) |
| [8] | Candotti, E., Palmieri, C., and Vitale, B. On the inversion of Noether's theorem in classical dynamical systems. American Journal of Physics, 40, 424-429 (1972) |
| [9] | Djukic, D. D. S. and Vujanovic, B. D. Noether's theory in classical nonconservative mechanics. Acta Mechanica, 23(1-2), 17-27 (1975) |
| [10] | Lutzky, M. Symmetry groups and conserved quantities for the harmonic oscillator. Journal of Physics A: Mathematical and General, 11(2), 249-258 (1978) |
| [11] | Zhao, Y. Y. Lie symmetries and conserved quantities of non-conservative mechanical system (in Chinese). Chinese Journal of Theoretical and Applied Mechanics, 26(3), 380-384 (1994) |
| [12] | Mei, F. X. Applications of Lie Groups and Lie Algebras to Constrained Mechanical Systems, Science Press, Beijing (1999) |
| [13] | Mei, F. X. Lie symmetries and conserved quantities of constrained mechanical systems. Acta Mechanica, 141(3-4), 135-148 (2000) |
| [14] | Zhang, H. B. Lie symmetries and conserved quantities of non-holonomic mechanical systems with unilateral Vacco constraints. Chinese Physics, 11(1), 1-4 (2002) |
| [15] | Mei, F. X. Symmetry and Conserved Quantity of Constrained Mechanical System, Beijing Institute of Technology Press, Beijing (2004) |
| [16] | He, G. and Mei, F. X. Three kinds of symmetry about nonholonomic-nonconservative systems. Journal of Beijing Institute of Technology, 27, 565-567 (2007) |
| [17] | Fu, J. L., Chen, B. Y., and Chen, L. Q. Noether symmetries of discrete nonholonomic dynamical systems. Physics Letters A, 373(4), 409-412 (2009) |
| [18] | Chen, X. W., Chang, L., and Mei, F. X. Conformal invariance and Hojman conserved quantities of first order Lagrange systems. Chinese Physics B, 17(9), 3180-3184 (2008) |
| [19] | Yang, S. P., Chen, L. Q., and Li, S. H. Dynamics of Vehicle-Road Coupled System (in Chinese), Science Press, Beijing (2012) |
| [20] | Lu, Y. J., Yang, S. P., Li, S. H., and Chen, L. Q. Numerical and experimental investigation on stochastic dynamic load of a heavy duty vehicle. Applied Mathematical Modelling, 34, 2698-2710 (2010) |
| [21] | Khalique, M. C. and Anjan, B. A Lie symmetry approach to nonlinear Schrödinger's equation with non-Kerr law nonlinearity. Communications in Nonlinear Science and Numerical Simulation, 14(12), 4033-4040 (2009) |
| [22] | Fu, J. L. and Chen, B. Y. Hojman conserved quantities and Lie symmetries of discrete nonconservative systems. Modern Physics Letters B, 23(10), 1315-1322 (2009) |
| [23] | Fu, J. L., Fu, H., and Liu, R. W. Hojman conserved quantities of discrete mechanico-electrical systems constructed by continuous symmetries. Physics Letters A, 374(17), 1812-1818 (2010) |
| [24] | Fang, J, H. A new type of conserved quantity of Lie symmetry for the Lagrange system. Chinese Physics B, 19(4), 21-24 (2010) |
| [25] | Fu, J. L., Li, X. W., Li, C. R., Zhao, W. J., and Chen, B. Y. Symmetries and exact solutions of discrete nonconservative systems. Science China Physics, Mechanics & Astronomy, 53(9), 1668-1706 (2010) |
| [26] | Fu, J. L., Chen, L. Q., and Chen, B. Y. Noether-type theorem for discrete nonconservative dynamical systems with nonregular lattices. Science China Physics, Mechanics & Astronomy, 53(3), 544-554 (2010) |
| [27] | Yang, S. P., Chen, L. Q., and Li, S. H. Dynamics of Vehicle-Road Coupled System, Science Press, Beijing (2012) |
| [28] | Zhou, S., Fu, H., and Fu, J. L. Symmetry theories of Hamiltonian systems with fractional derivatives. Science China Physics, Mechanics & Astronomy, 54(10), 1846-1852 (2011) |
| [29] | Fu, J. L., Chen, B. Y., Fu, H., Zhao, G. L., Liu, R. W., and Zhu, Z. Y. Velocity-dependent symmetries and non-Noether conserved quantities of electromechanical systems. Science China Physics, Mechanics & Astronomy, 54(2), 288-295 (2011) |
| [30] | Fu, J. L., Zhao,W. J., and Chen, B. Y. Energy-work connection integration schemes for mechanicoelectrical systems. Nonlinear Dynamics, 70(1), 755-765 (2012) |
| [31] | Mustafa, M. T. and Masood, K. Symmetry solutions of a nonlinear elastic wave equation with third-order an harmonic corrections. Appl. Math. Mech. -Engl. Ed., 30(8), 1017-1026 (2009) DOI 10.1007/s10483-009-0808-z |
| [32] | Rosmila, A. B., Kandasamy, R., and Muhaimin, I. Lie symmetry group transformation for MHD natural convection flow of nanofluid over linearly porous stretching sheet in presence of thermal stratification. Appl. Math. Mech. -Engl. Ed., 33(5), 593-604 (2012) DOI 10.1007/s10483-012-1573-9 |
| [33] | Fujii, T., Kudo, Y., Ohmura, Y., Suzuki, K., Kogo, J., Mizuno, Y., Kita, Z., and Sawada, M. Polarization properties of state-of-art lithography optics represented by first canonical coordinate of Lie group. Proceedings of the SPIE, 6520, 1-6 (2007) |
| [34] | Tucker, J. D., Azimi-Sadjadi, M. R., and Dobeck, G. J. Canonical coordinates for detection and classification of underwater objects from sonar imagery. OCEANS 2007-Europe, Aberdeen, 1-6 (2007) |
| [35] | Arnal, D., Currey, B., and Dali, B. Construction of canonical coordinates for exponential Lie groups. Transactions of the American Mathematical Society, 361, 6283-6348 (2009) |
| [36] | Pakdemirli, M. and Aksoy, Y. Group classification for path equation describing minimum drag work and symmetry reductions. Appl. Math. Mech. -Engl. Ed., 31(7), 911-916 (2010) DOI 10.1007/s10483-010-1325-x |
| [37] | Dillen, F., Nistor, A. I., and Munteanu, M. I. Canonical coordinates and principal directions for surfaces in H2 × R. Taiwanese Journal of Mathematics, 15(5), 2265-2289 (2011) |
 2014, Vol. 35
2014, Vol. 35

























































