Shanghai University
Article Information
- Ming ZHEN, Zhi-gang JIANG, Dian-yi SONG, Fei LIU. 2014.
- Analytical solutions for finite cylindrical dynamic cavity expansion in compressible elastic-plastic materials
- Appl. Math. Mech. -Engl. Ed., 35(8): 1039-1050
- http://dx.doi.org/10.1007/s10483-014-1842-7
Article History
- Received Jul. 10, 2013;
- Revised Nov. 14, 2013
The spherical and cylindrical cavity expansion solutions have been widely used to modelthe penetration problems of rock[ 1, 2 ] and metallic targets. Forrestal and his colleagues[ 3, 4, 5, 6, 7, 8, 9 ]developed spherical and cylindrical dynamic cavity expansion models for the penetration ofmetal targets with infinite dimensions. Forrestal and Luk[ 3 ] developed both a full-nonlinear and an approximate solution for the dynamic spherical cavity expansion in compressible elastic-plastic material,and the approximate solution was in good agreement with the full-nonlinearsolution for a practical expansion velocity range. Warren and Forrestal[ 7 ] further discussedthe effects of compressibility,strain hardening,and stain-rate sensitivity on the penetrationresistance of metal targets. Based on the dynamic cavity expansion solutions of strain hardeningmaterial,Forrestal and Warren[ 8, 9 ] presented analytical equations of penetration depth,ballisticlimits,and residual velocities for conical and ogive-nose rigid projectiles penetrating aluminumtarget plates. Further,Rosenberg and Dekel[ 10, 11, 12 ] conducted some studies on the spherical and cylindrical cavity expansion process,and Durban and Masri[ 13, 14, 15 ] extended the cavityexpansion models. So far,all the works mentioned above are for infinite spherical or cylindricalmodels without considering the free boundary of targets with finite dimensions. Littlefieldet al.[ 16 ] conducted penetration experiments and numerical simulations of tungsten-alloy long-rods projectiles into 4 340 steel cylindrical targets with various diameters,and proposed ananalytical model for target resistance based on cylindrical cavity expansion modeling. Allthe experimental,numerical and analytical results showed that the target resistance decreasedsignificantly as the diameter ratio of target to projectile fell below about 20. Macek and Duffey[ 17 ] developed a finite spherical cavity expansion model to consider the near-surface and layering effects of oblique earth penetration. In order to take into account of the effects ofthe free boundary on the penetration process,Jiang and his colleagues[ 18, 19, 20, 21, 22 ] proposed finitespherical and cylindrical cavity expansion models in incompressible elastic-plastic,linear strain-hardening,and exponential strain-hardening materials,and developed engineering models ofrigid sharp-nosed projectiles into metallic targets with finite thickness and long-rods projectilesinto thick metallic targets with finite radius.
As discussed by Jiang et al.[ 20 ],the dynamic cylindrical cavity expansion process in anelastic-plastic cylinder with an initial radius r0 can be divided into two continuous stages,thatis,an elastic-plastic stage followed by a plastic stage. The response regions in elastic-plasticstage are shown in Fig. 1(a)for t > t0 = r0/cd,where r is the Eulerian coordinate,rt is theradius of the deformed cylinder,rc = vct is the cavity radius at time t with conditions t =0,rc = 0,and constant expansion velocity vc,and vp and cd are the elastic-plastic interfacevelocity and the elastic dilatational velocity,respectively. When t < t0,the finite model isidentical with the infinite model since the elastic wave front does not reach the external surface.When the plastic wave front reaches the external surface,rp = rt,the elastic region disappears,and the first stage ends and the second stage starts. The response regions in plastic stage areshown in Fig. 1(b).
 |
| Fig. 1 Response regions of finite cylindrical cavity expansion |
In Ref. [ 20 ],Jiang et al. neglected the effects of compressibility,and took rt ≥ r0 to derivethe radial stress on cavity wall,which did not take into account of the effect of the radicaldisplacement at the external free surface. In this paper,we took rt > r0 for t > t0 = r0/cd,and developed analytical solutions for the dynamic cylindrical expansion in a compressibleelastic-plastic cylinder with a finite radius r0. In Section 2,we adopt the similarity transformmethod used by Forrestal and Luk[ 3 ] to derive the approximate solutions. In Section 3,weshow numerical results and comparisons with Ref. [ 20 ] to discuss the effects of the finite radius,material compressibility,and the radical displacement at the external free boundary.2 Finite cylindrical cavity expansion model for compressible elastic-plasticmaterials2.1 Momentum and mass conservation equations
In cylindrical cavity expansion problems,the plane-strain condition are implied,that isεd = 0,and the equations of momentum and mass conservation in Eulerian coordinates withcylindrical symmetry are as follows:
where σr and σθ are the radial and circumferential components of Cauchy stress,measuredpositive in compression,ρ = ρ(t,r)is the density in the deformed state,which can be regardedas ρ0(the density in the undeformed state)in the elastic region,v is the particle velocity inthe radial direction,with outward motion considered positive.2.2 Response of elastic-plastic stage(rp ≤ rt)2.2.1 Elastic regionIn the elastic region,rp ≤ r ≤ rt,σz = ν(σr + σθ),where ν is Poisson’s ratio. According tothe generalized Hooke law,the stress-displacement relation is expressed as follows:
where E is Young’s modulus,and u is particle radial displacement(positive outward).Since the particle velocity in the elastic region is likely to be negligible[ 3 ],neglecting theconvection term in(1) and substituting(3)into(1)give the wave equation
where

At the elastic-plastic interface and in the plastic region,the von-Mise yield criterion is obeyed
where σy is the yield stress.While t > t0 = r0/cd,we introduce the following similarity transforms[ 3 ]:
Then,(4)is converted into an ordinary differential equation,i.e.,whereα =vp/cd.
(7)can be reduced to a first-order differential equation of F(z),i.e.,
with the successive transformation[ 3 ] z = αξ,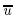 = zφ,F = dφ/dz .Integration of(8a)results in the following expression:where the integration constants A and B are evaluated from the yield condition at the elastic-plastic interface and the stress condition at the external boundary of the deformed cylinder.
= zφ,F = dφ/dz .Integration of(8a)results in the following expression:where the integration constants A and B are evaluated from the yield condition at the elastic-plastic interface and the stress condition at the external boundary of the deformed cylinder.
At the elastic-plastic interface,r = rp,ξ = 1,(5)is expressed as
At the external surface of the deformed cylinder,r = rt = r0 +ut,the radial stress is zero,thusThe constants A and B,the radial stress σr,and the particle velocity v are obtained from(3),(6),(8b),(9),and (10),where T = σy/K,K is the bulk modulus,and ξt is determined from(8b),(11a),and (11b)bysetting ξ = ξt,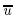 = ξt − ξ0,ξ0 = ry/rp.Setting ξ = 1 in(12) and (13)gives the particle velocity and radial stress at the elastic-plastic interface for t > t0 = r0/cd,As for t < t0 = r0/cd,the elastic wave front does not reach the external surface,but theradial stress at the elastic wave front r = cdt is zero. Setting ξt = 1/α in(11)-(15)can get theresults for t < t0,which are identical with those from the infinite cylindrical cavity expansionmodel[ 6 ].2.2.2 Plastic regionIn the plastic region,rc ≤ r ≤ rp,introducing the dimensionless variables and using the same methods in Ref. [ 3 ],we getwhere
= ξt − ξ0,ξ0 = ry/rp.Setting ξ = 1 in(12) and (13)gives the particle velocity and radial stress at the elastic-plastic interface for t > t0 = r0/cd,As for t < t0 = r0/cd,the elastic wave front does not reach the external surface,but theradial stress at the elastic wave front r = cdt is zero. Setting ξt = 1/α in(11)-(15)can get theresults for t < t0,which are identical with those from the infinite cylindrical cavity expansionmodel[ 6 ].2.2.2 Plastic regionIn the plastic region,rc ≤ r ≤ rp,introducing the dimensionless variables and using the same methods in Ref. [ 3 ],we getwhere

With the continuous conditions at the elastic-plastic interface and from(15) and (17),weobtain
At the cavity wall,let σr = σrc1. Then,We neglect the nonlinear terms in(17a) and (17b)as discussed by Forrestal[ 3 ],and thenobtain a linear ordinary differential equation of U(ξ),The solution of(20)that satisfies the boundary condition(18a)isWith the second equation in(19) and (21),we get the equation to determine vp = βc0,i.e.,where
 The radial stress σr is obtained from(17),(18b),and (21)as follows:
The radial stress σr is obtained from(17),(18b),and (21)as follows:
In the plastic stage,introducing the dimensionless variables
and using the same methods used in Ref. [ 3 ],we getwhere
 in which rt is simply determined according to mass conservation by taking ρ ≈ ρ0.
in which rt is simply determined according to mass conservation by taking ρ ≈ ρ0.
The boundary conditions at the cavity wall(r = rc,ζ = ζc = 1) and the external free surface(r = rt,ζ = ζt),respectively,are
To obtain analytical solutions as discussed by Forrestal[ 3 ],we neglect the nonlinear terms in(26a) and (26b) and combine(27) and (28)to getLet ζ = ζc = 1 in(30). Then,the cavity stress σrc2 in the plastic stage can be calculated by3 Numerical results and discussion
The deviation between the approximate and full-nonlinear solutions in Ref. [ 3 ] is less than5% for vc ≤ 3,which indicates that the approximate solutions in Section 2 are reliablefor vc
≤ 3,which indicates that the approximate solutions in Section 2 are reliablefor vc ≤ 3. We choose armor steel for discussion(E = 200.6 GPa,ν = 0.29,σy=1.365 GPa,ρ0 = 7 850 kg/m3,and the uniaxial tension fracture strain "f = 0.19).3.1 Process of finite cylindrical cavity expansion
≤ 3. We choose armor steel for discussion(E = 200.6 GPa,ν = 0.29,σy=1.365 GPa,ρ0 = 7 850 kg/m3,and the uniaxial tension fracture strain "f = 0.19).3.1 Process of finite cylindrical cavity expansion
Figure 2 shows the radial stress on cavity wall in the finite cavity expansion process. Thestress σrc remains constant and equates those from the infinite model while rp/r0≤ 0.39,0.01for vc = 300 m/s,10 m/s,respectively,which indicates that the elastic wave front does notreach the external surface,then the stress decreases moderately with the increase of rp/r0untilrp/r0 ≈1,which indicates that the stress on cavity wall decreases with the cavity expansion inelastic-plastic stage,and the stress decreases drastically during plastic stage(rp/r0>1).
 |
| Fig. 2 Radial stress on cavity wall in finite cylindrical cavity expansion process |
Figure 3 shows the radial stress profiles for rp/r0= 0.2,rp/r0= 0.6,and rp/r0= 1.1,which representthe infinite model,the elastic-plastic stage,and the plastic stage of the finite model,respectively.As shown,the radial stress decreases as r increases,and the stresses drop drastically across theplastic region. Moreover,the stress for rp/r0= 0.2 is higher than that for rp/r0= 0.6,and the stressin the plastic stage is much smaller than that in the elastic-plastic stage.
 |
| Fig. 3 Radial stress profiles for vc = 300 m/s |
Figure 4 shows the radial stress on cavity wall versus cavity expansion velocity in elastic-plastic stage for r0 = ∞,rp/r0= 1.0 presenting the infinite and finite cavity expansion models,respectively. The relative deviation between the infinite(r0 = 1) and finite(rpr0= 1.0)modelsrises steadily from 18.9% to 21.0% with the increasing of vc for vc = 0−0.56,then declinesslowly to 6.1% at vc
= 0−0.56,then declinesslowly to 6.1% at vc = 3.
= 3.
 |
| Fig. 4 Radial stress on cavity wall versus cavity expansion velocity in elastic-plastic stage with r0=∞ |
Figure 5 shows the radial stress on cavity wall versus cavity expansion velocity in plasticstage of the finite cavity expansion model at rc/r0= 0.3,0.4,and 0.5. As shown,the increaseof rc/r0leads to the decrease of σrc,the relative deviation of σrc between rc/r0= 0.3 and rc/r0= 0.5rises from 50% to 90% for vc = 0 − 3,which indicates that the radial stress on cavity walldecreases drastically with the decrease of r0 for the same rc.
= 0 − 3,which indicates that the radial stress on cavity walldecreases drastically with the decrease of r0 for the same rc.
 |
| Fig. 5 Radial stress on cavity wall versus cavity expansion velocity in plastic stage |
All the results of σrc in the elastic-plastic stage and plastic stage show that the less theinitial cylinder radius r0 is,the lower the radial stress on cavity wall is. It can be induced thatthe effects of finite radius should be considered in predicting the penetration resistance of metaltargets with relatively small radius.3.3 Comparisons with incompressible model
Jiang et al.[ 20 ] derived the response equations for the finite dynamic cylindrical cavity expan-sion of incompressible elastic-plastic materials by taking rt ≡ r0. We summarize these resultsin the following. The elastic-plastic interface velocity is given by
The cavity radius at the elastic-plastic stage end(rp = r0)isThe radial stress on cavity wall in elastic-plastic stage is expressed aswhere
 The radial stress on cavity wall in plastic stage is
The radial stress on cavity wall in plastic stage is
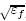 )r0 is the cavity radius at the plastic stage end.
)r0 is the cavity radius at the plastic stage end.
The cavity expansion velocity in(34) and (35)needs to satisfy the following condition:
As concluded in Refs. [ 3 ] and [ 7 ],the incompressible model leads to higher elastic-plastic inter-face velocity and radial stress on cavity wall. Figure 6 shows the elastic-plastic interface velocityversus the cavity expansion velocity,which agrees well with that in Ref. [ 3 ] and indicates thatthe larger vc is,the more the compressibility affects vp.  |
| Fig. 6 Elastic-plastic interface velocity versus cavity expansion velocity |
On the other h and ,taking r = r0 and σr = 0 leads to lower radial stress on cavity wall sincethere is radial displacement at the external free boundry and at r = r0,σr = σr0 > 0 underthe Eulerian coordinate. In the elastic-plastic stage,Fig. 7 shows the stress σr0 for rp/r0= 0.8,1.0,and Fig. 8 shows the results of the radial stress on the cavity wall,in which vc ≤ 1.4for(34)according to(36). As shown in Fig. 8,(34)agrees well with(24)for vc
≤ 1.4for(34)according to(36). As shown in Fig. 8,(34)agrees well with(24)for vc ≤ 1.4because the effect of taking r = r0 and σr = 0 compensates partially the effect of neglectingcompressibility in(34). It is noted that the results of(34)are higher than those of(24)whenvc
≤ 1.4because the effect of taking r = r0 and σr = 0 compensates partially the effect of neglectingcompressibility in(34). It is noted that the results of(34)are higher than those of(24)whenvc ≤ 0.9,0.79 for rp/r0= 0.8,1.0,respectively,which indicates that the effect of neglectingcompressibility dominates for very small σr0. However,σr0 rises with the increase of vc,asshown in Fig. 7,the effect of taking r = r0,σr = 0 becomes dominant and the results of(34)become less than those of(24),when vc
≤ 0.9,0.79 for rp/r0= 0.8,1.0,respectively,which indicates that the effect of neglectingcompressibility dominates for very small σr0. However,σr0 rises with the increase of vc,asshown in Fig. 7,the effect of taking r = r0,σr = 0 becomes dominant and the results of(34)become less than those of(24),when vc > 0.9,0.79 for rp/r0= 0.8,1.0,respectively. In theplastic stage,the displacement at free boundry is relatively large,thus as shown in Fig. 9,theresults of(35)are less than those of(31),and the deviation ascends with the increase of vc.
> 0.9,0.79 for rp/r0= 0.8,1.0,respectively. In theplastic stage,the displacement at free boundry is relatively large,thus as shown in Fig. 9,theresults of(35)are less than those of(31),and the deviation ascends with the increase of vc.
 |
| Fig. 7 Radial stress at r = r0 versus cavity expansion velocity in elastic-plastic stage |
 |
| Fig. 8 Radial stress on cavity wall versus cavity expansion velocity in elastic-plastic stage |
 |
| Fig. 9 Radial stress on cavity wall versus cavity expansion velocity in plastic stage with rc/r0 = 0.4 |
We have developed analytical solutions for the finite dynamic cylindrical expansion model ofcompressible elastic-plastic materials by taking into account of the effect of radical displacementat lateral free surface. The expansion process includes two continuous stages,namely,an elastic-plastic stage followed by a plastic stage. Numerical results and comparisons with Ref. [ 20 ] showthat the finite radius and the lateral free boundary have significant influence on the cavityexpansion process and the radial stress on the cavity wall in the plastic stage,but the influenceof compressibility and boundary displacement on the radial stress on the cavity wall can beneglected for vc ≤ 1.4 in the elastic-plastic stage. It is suggested that the effect of finiteradius should be considered in predicting the penetration resistance of metal targets with arelatively small radius.
≤ 1.4 in the elastic-plastic stage. It is suggested that the effect of finiteradius should be considered in predicting the penetration resistance of metal targets with arelatively small radius.
| [1] | Forrestal, M. J., Longcope, D. B., and Norwood, F. R. A model to estimate forces on conical penetrators into dry porous rock. Journal of Applied Mechanics, 48, 25-29 (1981) |
| [2] | Longcope, D. B. and Forrestal, M. J. Penetration of targets described by a Mohr-Coulomb failure criterion with a tension cutoff. Journal of Applied Mechanics, 50, 327-333 (1983) |
| [3] | Forrestal, M. J. and Luk, V. K. Dynamic spherical cavity-expansion in a compressible elastic-plastic solid. Journal of Applied Mechanics, 55, 275-279 (1988) |
| [4] | Forrestal, M. J., Luk, V. K., and Bar, N. S. Perforation of aluminum armor plates with conical-nose projectiles. Mechanics of Materials, 10, 97-105 (1990) |
| [5] | Luk, V. K., Forrestal, M. J., and Amos, D. E. Dynamic spherical cavity expansion of strain-hardening materials. Journal of Applied Mechanics, 58, 1-6 (1991) |
| [6] | Luk, V. K. and Amos, D. E. Dynamic cylindrical cavity expansion of compressible strain-hardening materials. Journal of Applied Mechanics, 58, 334-340 (1991) |
| [7] | Warren, T. W. and Forrestal, M. J. Effects of harding and strain-rate sensitivity on penetration of aluminum targets with spherical-nosed rods. International Journal of Solids and Structures, 35, 3737-3753 (1998) |
| [8] | Forrestal, M. J. and Warren, T. W. Penetration equations for ogive-nose rods into aluminum targets. International Journal of Impact Engineering, 35, 727-730 (2008) |
| [9] | Forrestal, M. J. and Warren, T. W. Perforation equations for conical and ogival nose rigid pro-jectiles into aluminum target plates. International Journal of Impact Engineering, 36, 210-215 (2009) |
| [10] | Rosenberg, Z. and Dekel, E. A numerical study of the cavity expansion process and its application to long-rod penetration mechanics. International Journal of Impact Engineering, 35, 147-154 (2008) |
| [11] | Rosenberg, Z. and Dekel, E. Analytical solution of the spherical cavity expansion process. International Journal of Impact Engineering, 36, 193-198 (2009) |
| [12] | Rosenberg, Z. and Dekel, E. The penetration of rigid rods-revisited. International Journal of Impact Engineering, 36, 551-564 (2009) |
| [13] | Durban, D. and Masri, R. Dynamic spherical cavity expansion in an elastoplastic compressible Mises solid. International Journal of Solids and Structures, 41, 5697-5716 (2004) |
| [14] | Masri, R. and Durban, D. Dynamic spherical cavity expansion in a pressure sensitive solid. Journal of Applied Mechanics, 72, 887-898 (2005) |
| [15] | Masri, R. and Durban, D. Deep penetration analysis with dynamic cylindrical cavitation fields. International Journal of Impact Engineering, 36, 830-841 (2009) |
| [16] | Littlefield, D. L., Anderson, C. E., Partom, Y., and Bless, S. J. The penetration of steel targets finite in radial extent. International Journal of Impact Engineering, 19, 49-62 (1997) |
| [17] | Macek, R. W. and Duffey, T. A. Finite cavity expansion method for near-surface effects and layering during Earth penetration. International Journal of Impact Engineering, 24, 239-258 (2000) |
| [18] | Jiang, Z. G., Zeng, S. Y., and Zhou, J. P. An analytical model for penetration into finite thickness metallic target struck by rigid sharp-nosed projectiles (in Chinese). Acta Armamentarii, 28(8), 923-929 (2007) |
| [19] | Jiang, Z. G., Zeng, S. Y., and Zhou, J. P. A Three-stage model for the perforation of moderately thick metallic plates (in Chinese). Acta Armamentarii, 28(9), 1046-1052 (2007) |
| [20] | Jiang, Z. G., Song, D. Y., and Zeng, S. Y. A finite cylindrical cavity expansion theory and its application (in Chinese). Journal of Vibration and Shock, 30(4), 139-143 (2011) |
| [21] | Song, D. Y., Liu, F., and Jiang, Z. G. An analytical model for penetration into cylindrical metallic thick target by rigid sharp-nosed projectiles (in Chinese). Engineering Mechanics, 31(1), 31-36 (2013) |
| [22] | Jiang, Z. G., Song, D. Y., and Liu, F. A finite cylindrical cavity expansion and penetration model of exponential strain-hardening materials. Advanced Materials Research, 634-638, 2781-2786 (2013) |
 2014, Vol. 35
2014, Vol. 35

































