Shanghai University
Article Information
- Bo-ling GUO, Guo-li ZHOU. 2014.
- Exponential stability of stochastic generalized porous media equations with jump
- Appl. Math. Mech. -Engl. Ed., 35(8): 1067-1078
- http://dx.doi.org/10.1007/s10483-014-1845-7
Article History
- Received Sept. 6, 2013;
- Revised Jan. 25, 2014
2. College of Mathematics and Statistics, Chongqing University, Chongqing 401331, P. R. China
1 Introduction Stochastic partial differential equations with jump have been extensively studied in recent years. There exists a great number of works on the subject in literature,see the monograph[1] and the references therein. The stability of stochastic partial differential equations has also been extensively studied; for its theory and various applications (such as applications in finance and automatic control),the reader is referred to Refs. [2, 3, 4] and the references therein. The stability of a linear equation with jump coefficient was studied in Ref. [4]. In Ref. [5],the stability of a semilinear stochastic differential equation with Wiener process was investigated. The exponen- tial stability of general nonlinear stochastic differential equations with Wiener processes was studied in Ref. [6]. The asymptotic and exponential stability of the nonlinear stochastic delay differential equations withWiener processes were considered in Ref. [7] and Ref. [8],respectively. In Ref. [9],the stability of infinite dimensional stochastic evolution equations with memory and Lévy jumps was studied.
In this article,the aim is to consider the following stochastic partial differential equation:
where L is a partial (or pseudo) differential operator of order (less than or equal to) two,e.g., L = Δ (or L = −(−Δ)α,α ∈ (0,1]) on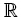 or an open subset thereof. The maps
or an open subset thereof. The maps 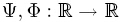 are assumed to fulfill certain monotonicity conditions. Q is a Hilbert-Schmidt operator valued
Lipschitz map,and F denotes a Lipschitz map taking values in a Hilbert space. W stands for the cylindrical wiener process and is defined on a complete probability space (Ω
,F,P) with
normal filtration Ft = σ{W(s) : s ≤ t},t ∈ [0,T]. N(dt,dz) represents the Poisson random
measure associated with compensated (Ft)-martingale measure defined as
where λ(dz),defined on the separable Banach space Z,is the intensity measure of N(dt,dz).
In particular,if Φ = 0,Q = 0,F = 0,and Ψ(s) := |s|r−1s for some r > 1,then (1) reduces
back to the classical porous medium equation (e.g.,see Ref. [10]) as follows:
Furthermore,if L is the Dirichlet Laplacian on an open bounded domain in
are assumed to fulfill certain monotonicity conditions. Q is a Hilbert-Schmidt operator valued
Lipschitz map,and F denotes a Lipschitz map taking values in a Hilbert space. W stands for the cylindrical wiener process and is defined on a complete probability space (Ω
,F,P) with
normal filtration Ft = σ{W(s) : s ≤ t},t ∈ [0,T]. N(dt,dz) represents the Poisson random
measure associated with compensated (Ft)-martingale measure defined as
where λ(dz),defined on the separable Banach space Z,is the intensity measure of N(dt,dz).
In particular,if Φ = 0,Q = 0,F = 0,and Ψ(s) := |s|r−1s for some r > 1,then (1) reduces
back to the classical porous medium equation (e.g.,see Ref. [10]) as follows:
Furthermore,if L is the Dirichlet Laplacian on an open bounded domain in 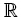 d,it is well known
that the solution decays algebraically fast in t. We refer to Refs. [2, 10, 11] and the references
therein,also for historical remarks. In this article,under some monotonicity assumptions,we
obtain the moment exponential stability and the almost certain exponential stability of the
stochastic generalized porous media equations with jump.
d,it is well known
that the solution decays algebraically fast in t. We refer to Refs. [2, 10, 11] and the references
therein,also for historical remarks. In this article,under some monotonicity assumptions,we
obtain the moment exponential stability and the almost certain exponential stability of the
stochastic generalized porous media equations with jump.In recent years,the stochastic version of the porous medium equation with Brownian motion has been studied intensively,see Refs. [12, 13, 14, 15, 16, 17, 18, 19, 20, 21] and the references therein. However,as far as we know,there have been few works that deal porous media equation with jump noise. As jump noise is different from wiener noise,this will bring various new difficulties from calculation and probability when stochastic equations with jump noise are considered. The method used in this article follows that Refs. [22, 23]. In Ref. [23],the existence and uniqueness of stochastic gener- alized porous media equations with L`evy jump were obtained,and in Ref. [24],the ergodicity of the same equation was obtained. In this article,the moment exponential stability is obtained, and then it is used to establish the almost certain exponential stability of the equations. 2 Some preliminaries
Let ( ,M,υ) be a separable probability space and (L,D(L)) a negative definite self-adjoint
linear operator on L2(υ) having discrete spectrum with eigenvalues
,M,υ) be a separable probability space and (L,D(L)) a negative definite self-adjoint
linear operator on L2(υ) having discrete spectrum with eigenvalues
Before stating our equation,we first introduce the state space of the solutions. Let
Define H to be its dual space with inner product <·,·>. Identify L2(υ) with its dual. We get the continuous and dense embedding We denote the duality between H and H1 by <·,·>. Obviously,when restricted to L2(υ) × H1, this coincides with the inner product in L2(υ),which is also denoted by <·,·>. It is clear that Let LHS be the space of all Hilbert-Schmidt operators from a separable Hilbert space U to L2(υ). Let Wt denote the cylindrical Brownian motion on U w.r.t. a complete filtered probability space (Ω ,F,P). Let Ψ and Φ be nonlinear deterministic continuous functions on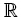 satisfying
where
Denote
A very simple example satisfying (3)-(4) is that
Let
be progressively measurable such that
where μ > 0,and for arbitrary δ > 0,the nonnegative continuous function h(t) with t ∈
satisfying
where
Denote
A very simple example satisfying (3)-(4) is that
Let
be progressively measurable such that
where μ > 0,and for arbitrary δ > 0,the nonnegative continuous function h(t) with t ∈ 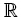 +
satisfies
i.e.,
and x,y ∈ H. From Kuratowski’s theorem,we know B(L2(υ)) ⊂ B(H). Let
be B(
+
satisfies
i.e.,
and x,y ∈ H. From Kuratowski’s theorem,we know B(L2(υ)) ⊂ B(H). Let
be B(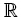 +) × B(H) × B(Z)/B(L2(υ))-measurable and satisfy
where η1(t)(t ∈
+) × B(H) × B(Z)/B(L2(υ))-measurable and satisfy
where η1(t)(t ∈ 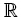 +) is a nonnegative continuous function and for arbitrary δ > 0 satisfies
i.e.,
and y,y1,y2 ∈ H.
+) is a nonnegative continuous function and for arbitrary δ > 0 satisfies
i.e.,
and y,y1,y2 ∈ H.
Remark 1 Since h(t) = o(eμt) and η1(t) = o(eμt),there exists a positive constant γ such
that h(t)e-μt ≤ γ,η1(t)e-μt ≤ γ for all t ∈ 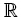 +.
+.
We say mapping  : [0,∞[→ H is right continuous and left hand limits (RCLL) if it is right
continuous and its left limits exist. Then,we introduce the definition of the solution to (1).
: [0,∞[→ H is right continuous and left hand limits (RCLL) if it is right
continuous and its left limits exist. Then,we introduce the definition of the solution to (1).
Defintion 1 An H-valued RCLL (Ft)-adapted process X(t) is called a solution to (1),if
X ∈ Lr+1([0,T] ×Ω
×  ; ds × P × υ) such that for any i ∈
; ds × P × υ) such that for any i ∈ ,
,
We define V :=Lr+1(υ). As H is a Hilbert space,we identify H* with H via the Riesz isomorphism. Then,we have
continuously and densely. In order to rewrite (9) in vector form,we need two lemmas from Ref. [15]. For the reader’s convenience,we cite them in the following.Lemma 1[15] The linear operator
defines an isometry from L(r+1)/r(υ) to V* with a dense domain. Its unique continuous ex- tension L to all of L(r+1)/r(υ) is an isometric isomorphism from L(r+1)/r(υ) onto V* such that Lemma 2[15] Let (L−1)′ : L(r+1)/r(υ) → L(r+1)/r(υ) be the dual operator of L−1 : Lr+1(υ) → Lr+1(υ). Then,the operator extends the natural inclusion L2(υ) ⊂ H ⊂ V*,and for all f ∈ L(r+1)/r(υ),g ∈ Lr+1(υ) According to the above lemmas,we have In view of (3)-(4),Lemma 1,and Lemma 2,the integral is well defined in V*. Thus,(9) can be rewritten in vector form as Before giving our main result,we need a theorem from Ref. [23],which for convenience is cited here.Theorem 1[23] Assume that conditions from (3) to (8) hold,and let X0 ∈ L2(Ω ,F0,P;H). Then,there exists a unique solution to (1) in the sense of Definition 1. Moreover,
3 Main resultsWith all preparations above,we are now in the position of stating our main results in this paper.
Theorem 2 In addition to conditions (3)-(8),we assume that Ψ(0) = 0,and Φ(0) = 0. Then,if Xt is a global strong solution to (1),there exists C > 0 such that
Proof Let ε be a very small positive constant such that μ − ε > 0. Then,Itô’s formula implies
By (4) and Ψ(0) = 0,as well as Φ(0) = 0,we get Thus, where the last inequality follows the Young inequality. Since the last two terms on the right hand side of (13) are martingales,we have Since from (14) and the Gronwall inequality,we have Finally,we get In the following,we intend to investigate the almost certain stability,which is in most situations the kind of stability one usually wants to have in practical applications,of the trivial solution of (1).Theorem 3 Under the conditions in Theorem 2,there exist positive constants M,ε,and a subset Ω0 ⊂ Ω with P(Ω 0) = 1 such that,for each w ∈ Ω 0,there exists a positive random number T (w) such that
Proof For 0 ≤ s ≤ t,by (5) and (11),we have where Similarly,by (7) and (11),we have where In the following,we prove that there exists a positive constant M > 0 such that By Itô’s formula,we have By Burkholder-Davis-Gundy’s inequality and (15),we get for any T ∈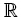 +,
where M1 and M2 are two positive constants and are independent of T . By the Burkholder-Davis-Gundy inequality and (16),we have
where M3 and M4 are independent of T . By Itô’s formula and (4),after some elementary
calculations,we get
By (11),(18),and (19),we have
where
Thus,we have
Since for arbitrary δ > 0,h(t)eδt and η1(t)eδt are continuous and subexponential growth,by
the Fatou lemma,we get
Finally,we are going to finish the proof. By Itô’s formula,after some elementary calculations,
we get
In the following,the positive constant C will change from line to line. By Burkholder-Davis-
Gundy’s inequality,(15),and (16),we get
Similar to the derivation of (19),we get
where the second inequality follows (16). From (20)-(22),we get
Thus,it follows that
where α = min{2θ,μ − ε}. From (20),we have
Let
From (21)-(23),we get
Thus,by Borel-Cantelli’s lemma,we complete the proof.
+,
where M1 and M2 are two positive constants and are independent of T . By the Burkholder-Davis-Gundy inequality and (16),we have
where M3 and M4 are independent of T . By Itô’s formula and (4),after some elementary
calculations,we get
By (11),(18),and (19),we have
where
Thus,we have
Since for arbitrary δ > 0,h(t)eδt and η1(t)eδt are continuous and subexponential growth,by
the Fatou lemma,we get
Finally,we are going to finish the proof. By Itô’s formula,after some elementary calculations,
we get
In the following,the positive constant C will change from line to line. By Burkholder-Davis-
Gundy’s inequality,(15),and (16),we get
Similar to the derivation of (19),we get
where the second inequality follows (16). From (20)-(22),we get
Thus,it follows that
where α = min{2θ,μ − ε}. From (20),we have
Let
From (21)-(23),we get
Thus,by Borel-Cantelli’s lemma,we complete the proof.Acknowledgements The authors would like to thank the editor and the anonymous referees for their careful reading of the manuscript and valuable suggestions.
| [1] | Peszat, S. and Zabczyk, J. Stochastic Partial Differential Equation with Lévy Noise: an Evolution Equation Approach, Cambridge University Press, Cambridge (2007) |
| [2] | Da Prato, G. and Zabczyk, J. Stochastic Equations in Infinite Dimensions, Cambridge University Press, Cambridge (1992) |
| [3] | Liu, K. Stability of Infinite Dimensional Stochastic Differential Equations with Applications, CRC Press, Boca Raton (2006) |
| [4] | Mariton, M. Jump Linear Systems in Automatic Control, CRC Press, Boca Raton (1990) |
| [5] | Basak, G. K., Bisi, A., and Ghosh, M. K. Stability of a random diffusion with linear drift. Journal of Mathematical Analysis and Applications, 202, 604-622 (1996) |
| [6] | Mao, X. Stability of stochastic differential equations with Markovian switching. Stochastic Pro-cesses and Their Applications, 79, 45-67 (1999) |
| [7] | Mao, X. Asymptotic stability for stochastic differential delay equations with Markovian switching. Functional Differential Equations, 9, 201-220 (2002) |
| [8] | Mao, X., Matasov, A., and Piunovskiy, A. Stochastic differential delay equations with Markovian switching. Bernoulli, 6(1), 73-90 (2002) |
| [9] | Luo, J.W. and Liu, K. Stability of infinite dimensional stochastic evolution equations with memory and Markovian jumps. Stochastic Processes and Their Applications, 118, 864-895 (2008) |
| [10] | Aronson, D. G. The porous medium equation. Lecture Notes in Mathematics, 1224, 1-46 (1986) |
| [11] | Aronson, D. G. and Peletier, L. A. Large time behaviour of solutions of the porous medium equation in bounded domains. Journal of Differential Equations, 39, 378-412 (1981) |
| [12] | Beyn, W. J., Gess, B., Lescot, P., and Röckner, M. The global random attractors for a class of stochastic porous media equations. Communications in Partial Differential Equations, 36, 446-469 (2011) |
| [13] | Da Prato, G. and Röckner, M. Weak solutions to stochastic porous media equations. Journal of Evolution Equations, 4, 249-271 (2004) |
| [14] | Da Prato, G. and Röckner, M. Invariant measures for a stochastic porous media equation. Advances in Pure Mathematics, 41, 13-29 (2004) |
| [15] | Da Prato, G., Röckner, M., Rozovskii, B. L., and Wang, F. Y. Strong solutions of stochastic generalized porous media equations: existence, uniqueness and ergodicity. Commnications in Partial Differential Equations, 31, 277-291 (2006) |
| [16] | Ebmeye, C. Regularrity in Sobolev spaces for the fast diffusion and the porous medium equation. Journal of Mathematical Analysis and Applications, 307, 134-152 (2005) |
| [17] | Ren, J., Röckner, M., and Wang, F. Y. Stochastic generalized porous meadia and fast diffusion equation. Journal of Differential Equations, 238, 118-152 (2007) |
| [18] | Kim, J. U. On the stochastic porous medium equation. Journal of Differential Equations, 206, 163-194 (2006) |
| [19] | Röckner, M. and Wang, F. Y. Non-monotone stochastic generalized porous media equations. Journal of Differential Equations, 245, 3898-3935 (2008) |
| [20] | Röckner, M., Wang, F. Y., andWu, L. M. Large deviations for stochastic generalized porous media equations. Stochastic Processes and Their Applications, 116, 1677-1689 (2006) |
| [21] | Wang, F. Y. Harnack inequality and applications for stochastic generalized porous media equations. Annals of Probability, 35(4), 1333-1350 (2006) |
| [22] | Caraballo, T. and Liu, K. On the exponential stability criteria of stochastic partial differential equations. Stochastic Processes and Their Applications, 83, 289-301 (1999) |
| [23] | Zhou, G. L. and Hou, Z. T. Stochastic generalized porous media equations with Lèvy jump. Acta Mathematica Sinica, 27, 1671-1696 (2011) |
| [24] | Zhou, G. L. and Hou, Z. T. The ergodicity of stochastic generalized porous media equations with Lévy jump. Acta Mathematica Scientia, 31, 925-933 (2011) |
 2014, Vol. 35
2014, Vol. 35

































































