1 Introduction

The linear-quadratic (LQ) optimal control problem has always been viewed as the fundamental problem of the optimal control theory. It is usually used as an important tool for practical aerospace control engineering. Its applications include planning spacecraft rendezvous utilizing a finite low thrust,satellite formation flying,station keeping and/or reconfiguration technology,and reentry vehicle trajectory guidance. Indeed,the maximum thrust and the momentum provided by the engine are both finite. Therefore,the LQ optimal control problem with control inequality constraints is commonly encountered and difficult to be solved.

From the feedback control law viewpoint,Kojima and Morari ^[1] introduced singular value decomposition for the finite time horizon linear systems,and obtained the sequence of LQ sub-optimal control laws,which was converged to an exact solution,based on quadratic programming. Bemporad et al. ^[2] proposed an explicit solution for the model predictive control based on a linear programming method. To decrease the online computation work of the model predictive control,Bemporad et al.^[3] solved the explicit solution of the feedback gain for the LQ optimal control with state and control constraints. Goebel and Subbotin ^[4] studied a continuous-time infinite-horizon linear quadratic regulator with input constraints.

From the trajectory optimization viewpoint,the numerical methods used to solve the optimal control problem can be divided into two major classes: the indirect methods and the direct methods ^{[5, 6]} . The indirect methods can transform the optimal control problem into a Hamiltonian boundary value problem (HBVP) by the calculus of variations or the maximum principle. The obtained HBVP can then be solved by the numerical methods such as the shooting method ^[7] and the multiple-shooting method ^[8] . The primary advantages of the indirect methods are the high accuracy in the solution and the assurance that the solution satisfies the first-order optimality conditions. However,the indirect methods have several disadvantages, including the small radii of convergence and the need to analytically derive the HBVP and an initial guess for the costate ^[9] . With the direct methods,the optimal control problem can be discretized and converted into parameter optimization problems,which can be solved by a nonlinear programming method ^{[10, 11]} . With different discretization schemes for the control and state variables,various direct methods are derived,e.g.,the local collocation methods ^{[12, 13]} , the global collocation methods ^{[14, 15]} ,and the time finite element methods ^{[16, 17]} . The direct methods are more advantageous than the indirect methods because they have larger radii of convergence and require no initial guess for the costate. However,for most direct methods,the solutions do not satisfy the first-order optimality conditions,and the costate variables cannot be estimated.

The present work involves conducting a numerical analysis of an LQ optimal control problem with control inequality constraints by using an adjustable or a variable parameter multiplier. The concept of a variable parameter multiplier was first introduced by Zhong and Zhang ^[18] to obtain the numerical solutions for elastoplastic structures and contact problems. In this paper, the variable parameter multiplier theory is generalized to develop a new numerical approach for analyzing the LQ optimal control problems with control inequality constraints. In the development of the approach,two fundamental issues have been addressed. First,a variable parameter is introduced to replace the inequality constraints by equality constraints. Under the equality constraints of the LQ optimal control problem,the parametric variational principle can be used to derive the Hamiltonian canonical equations coupled with the linear complementarity equations. Second,because the numerical solutions of the LQ optimal control problem can only be obtained at discrete-time points,the continuous time domain can be divided into a series of intervals. The linear complementarity solver is used to solve the variable parameters for all discrete-time points. In the proposed method,the control variable is expressed explicitly by the parametric variables,whereas in the indirect method,the control variable is determined implicitly by minimizing the Hamiltonian function. Nonetheless,the linear complementarity problem obtained in this paper is different from the programming problem obtained by direct methods. The solution of the proposed method satisfies the Hamiltonian canonical equations and provides the costate information.

The pseudospectral method for solving optimalcontrol problems has been studied and used widely from theory to practical applications ^{[9, 14, 15, 19, 20, 21, 22, 23, 24]} recently,and more and more atten-tion has been paid to it. A pseudospectral method,which belongs to the global collocation methods,is typically used in a single mesh interval,and the convergence is achieved by increasing the degree of the polynomial. Some pseudospectral methods can also be used to establish the costate mapping theorem,and the costate variables can be estimated by the Lagrange multipliers^{[9, 14, 15]} . For problems where the solutions are infinitely smooth and well behaved, a pseudospectral method has a simple structure and converges at an exponential rate ^{[19, 20]} . However,the convergence rate of a pseudospectral method for a problem whose formulation or solution is nonsmooth may be extremely slow,resulting in a poor approximation even when a high-degree polynomial is used ^{[19, 20, 21, 22]} . The pseudospectral method exhibits the well-known Gibbs phenomenon,resulting from the approximation of a nonsmooth function by a finite number of smooth functions ^{[21, 23]} . In addition,the limitation of a global pseudospectral method is that the use of high-degree global polynomials results in a nonlinear programming problem (NLP) for which the density grows quickly as a function of the number of the NLP variables. Thus,a global pseudospectral method becomes computationally intractable for the problems when an excessively large-degree polynomial is required ^{[19, 20]} .

For an LQ optimal control problem with control inequality constraints,the solutions of control variables are nonsmooth. Unlike the global pseudospectral method,variable parameter multipliers are used in many mesh intervals,and the solutions of the LQ optimal control problem are determined by these local variable parameter multipliers. Therefore,the well-known Gibbs phenomenon will not occur,and the convergence of the proposed method,which will not be influenced by the nonsmooth character,is achieved by increasing the number of the mesh intervals. Meanwhile,the costate variables can be evaluated by the variable parameter multipliers,and then the first-order optimality conditions can be checked. In addition,with the increase in the mesh intervals,the linear complementarity problem formulated by the proposed method is sparse. Thus,the computational efficiency of a sparse problem is better than that of a density problem with the same number of mesh intervals. The new low-order variable adaptive techniques ^[19] and the new mesh refinement techniques ^[22] are developed to increase the ability of pseudospectral methods. 2 LQ optimal control problems with control inequality constraints

The LQ optimal control problems with control inequality constraints in a finite continuoustime domain are considered in this paper. The linear differential equation for a controlled system can be expressed in the form of a state space as follows: ˙

where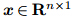 is a state variable, 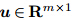is a control variable, 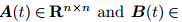R^n×m are the coefficient matrices,andx0is the initial condition of the controlled system. The control variableuis not free and is constrained by the following inequality: where C ∈R^p×m is a constant weighted matrix,and 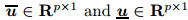are the upper and lower limits of the control variableu,respectively. The LQ optimal control problem is defined by minimizing the following performance indexJunder the constraints of Eqs. (1) and (2): wheretf is the given control time,and is assumed to be fixed,and Q(t)∈R^n×n ,R(t)∈R^m×m , and S_f ∈R^n×n are the weighted matrices. The weighted matrices Q(t) and S_f are nonnegative symmetric matrices,and R(t) is a positive definite symmetric matrix.

For an LQ optimal control problem,the boundary condition at the terminal time is

For an LQ optimal control problem with hard terminal constraints,the terminal boundary condition is

where x_f is the given terminal state. In the following sections,a parametric variational principle and the corresponding numerical algorithm are proposed to solve the LQ optimal control problem with control inequality constraints. 3 Parametric variational principle for LQ optimal control problems with control inequality constraints

In this section,based on the parametric variational principle ^{[18, 25, 26]} ,theLQoptimalcontrol problem with control inequality constraints is transformed into the Hamiltonian canonical equations coupled with the linear complementarity equation. The parametric variational principle can be used to overcome the limitations of the classical variational method ^{[18, 25, 26]} and address the inequality constraints.

By introducing the variables and ,Eq. (2) can be transformed into the following constraints:

With the Lagrange multiplier method,an expanded performance index,J_A,can be given as follows: with where λ,,and are the Lagrange multipliers. Performing the calculus of variations with respect to the control variableugives The above equation gives the following explicit expression for the control variableu: Substituting Eq. (11) into the Hamiltonian function (9),we can obtain a new Hamiltonian function that only depends on the state variable,the costate variable,and the parametric variable multipliers. Because the parametric variables and are not involved in the variations,some terms in the Hamiltonian function that are not related to the state and costate variables can be neglected,and a new Hamiltonian function can be given by Based on the parametric variational principle ^{[18, 25, 26]} ,the necessary condition for the optimal control is where δ_x,λ denotes the calculus of variations with respect to the state variablexand the costate variable λ. Substituting Eq. (12) into Eq. (13) gives the following Hamiltonian canonical equations: Meanwhile,the LQ optimal control problem must satisfy the equality constraint given by Eqs. (6) and (7). With Eq. (11),the equality constraint given by Eqs. (6) and (7) can be written as Furthermore,based on the parametric variational principle ^{[18, 25, 26]} ,thevariablesαandαand the parametric variables and must satisfy the following complementarity conditions: Thus,the LQ optimal control problem with control inequality constraints can be transformed into the Hamiltonian canonical equations (see Eqs. (14) and (15)) and the linear complementarity problem (see Eqs. (16)-(19)),which are coupled by the unknown parametric variables and .

Because the computation of the parametric variables and is essential to solve the LQ optimal control problem with control inequality constraints,the next section focuses on numerically determining the parametric variables by dividing the continuous time into a series of discrete intervals with the linear complementarity solver. The state variablex,thecostate variable λ,and the control variableucan be obtained through the known parametric variables.

Note that the above procedure is different from the Hamiltonian boundary value problem derived by the indirect method. In the indirect method,the control variable is determined implicitly by minimizing the Hamiltonian function,while the control variable is expressed explicitly by the parametric variables in this paper. 4 Numerical method to solve coupled Hamiltonian canonical equations and linear complementarity problem

In the previous section,the coupled Hamiltonian canonical equations and the linear complementarity equations are established. These coupled equations are difficult to be analytically solved in a continuous time domain. Therefore,in this paper,the continuous time is divided into a series of time intervals,and the state variables,the costate variables,and the control variables are solved on these discrete time points.

The Hamiltonian canonical equations (14) and (15) can be rewritten as

where The solution of the linear ordinary differential equation (20) can be expressed by where u₀ is the initial value of the ordinary differential equation,and Φ_k(·,·) denotes the transfer matrix.

For the numerical simulation,the continuous-time domain is divided into a series of intervals of equal length,i.e.,

whereηis the length of a time interval,and Nis the number of the intervals. In this paper, within a time interval [t_k−1,tk](k=1,2,···,N),the parametric variables and are approximated as the constant vectors _k and _k ,and the variables and are approximated as the constant vectors _k and _k. We also assume that the complementarity conditions in Eqs. (16)-(19) are satisfied at the discrete time,i.e., With the above assumptions,the solution of the ordinary differential equation (20) can be obtained at the timetkas follows: wherek=0,1,···,N,and The matrices in Eqs. (29) and (30) can be rewritten in the block form as follows: Then,according to Eqs. (28) and (31),the relationship between the state and costate variables at the initial time,i.e., and the state and costate variables at the terminal time,i.e., is given by the following equations: For the LQ optimal control problem,with the terminal condition given by Eq. (4),from Eqs. (32) and (33),we can obtain the initial costate variableλ0as follows: For the LQ optimal control problem with hard terminal constraints,using Eq. (5),the initial costate variable λ₀ can be obtained from Eq. (32) as follows: Then,using Eq. (28),the following equation can be obtained: where For the LQ optimal control problem,by substituting Eq. (34) into Eq. 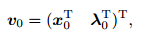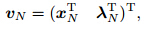(36),the costate variable can be expressed in terms of the unknown variables and . Substituting the expression of into Eqs. (24) and (25) gives a linear complementarity problem as follows: where

For the LQ optimal control problem with hard terminal constraints,the linear complementarity problem is the same as that of Eqs. (43)-(53) except forM1andqwhich are now given by

Thus,the coupled Hamiltonian canonical equations and the linear complementarity equations can be transformed into a linear complementarity problem of Eqs. (43)-(45). The linear complementarity problem can be solved by the pivotal method ^[27] ,the interior point method ^[28] , etc. In this paper,the Lemke algorithm,which belongs to the pivotal method category,is used to solve the linear complementarity problem.

Note that the linear complementarity problem of Eqs. (43)-(45) can be obtained by assuming that the continuous-time linear complementarity problem of Eqs. (16)-(19) is satisfied at the right point of each time interval. This is not the only choice. The similar linear complementarity problem can also be derived if the continuous-time linear complementarity problem of Eqs. (16)- (19) is satisfied at the left or at the middle point ofevery time interval. Moreover,the parametric variables in every time interval can be linearly approximated to derive the discrete-time linear complementarity problem.

For the LQ optimal problems with control inequality constraints,by solving the linear complementarity problem with the famous Lemke algorithm,the parametric variables and in all time intervals can be obtained. Then,the state,costate,and control variables can be computed directly. For the LQ optimal control problems,the state and the costate variables are given by Eqs. (28) and (34),respectively,and the control input is given by Eq. (11). For the LQ optimal control problems with hard terminal constraints,the state and costate variables can be computed by Eqs. (28) and (35),respectively,and the control input is also determined by Eq. (11).

It is important to note that the linear complementarity problem obtained in this paper is different from the quadratic programming (QP) problem obtained by the local direct collocation method for the LQ optimal control problem. The solution of the linear complementarity problem satisfies the Hamiltonian canonical equations,and it gives the costate information that can be used for the error analysis and solution verification. However,the solution of the local direct collocation method does not satisfy the first-order necessary condition of the optimal control, and it is uncertain whether the direct solution of the QP problem is truly optimal for the original continuous LQ optimal control problem ^[29] . 5 Computation of transfer matrix and related integration

In Section 4,to solve the LQ optimal control problem with control inequality constraints, one of the main problems is to calculate the transfer matrix and its related integration,i.e., Eqs. (29) and (30). The calculation of the transfer matrix can be divided into two categories: the time-invariant system (i.e.,the coefficient matrices of the system equation,Eq. (1),and the performance index,Eq. (3),are independent of time) and the time-varying system (i.e.,the coefficient matrices of the system equation and the performance index are related to time).

For the time-invariant systems,the coefficient matrices A(t) and B(t) of the system equation,Eq. (1),and the weighted matrices Q(t)and R(t) of the performance index,Eq. (3),are constant matrices. Therefore,the matrices A_k,B_k,Q_k,and R_k(k=1,2,···,N)areallthe same. Moreover,it is easy to prove that,for time-invariant systems,the corresponding transfer matrix only depends on the matrix and the length of the interval. Thus,the transfer matrix and its related integration,which are given by Eqs. (1) and (3),can be simplified as

where exp (·) denotes the matrix exponential. In general,the matrix exponential in Eq. (56) can be computed by the expm function in the MATLAB software. However,to achieve better precision,the precision integration method is used in this paper to compute the matrix exponential.

For the time-varying systems,the coefficient matricesA(t)andB(t)ofEq.(1)andthe weighted matrices Q(t)and R(t) of Eq. (3) depend on time,and the precision integration method cannot be used directly to compute the transfer matrix and its integration. In this paper,the Magnus series method ^{[30, 31]} ,a structure-preserving numerical algorithm,is used to calculate the transfer matrix for the time-varying systems.

The transfer matrix of the time-varying systems can be expressed by the matrix exponential of the Magnus series,i.e.,

where the Magnus series Ω(t,0) is defined as in which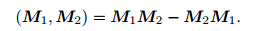

Iserles and Nørsett ^[30] studied the general form of the Magnus series. With a two-stage Gauss quadrature formula to Eq. (58),they gave an approximate formula for the Magnus series. According to their results,in a time interval [t_k−1,t_k],the transfer matrix can be given as the matrix exponential of an approximation of the Magnus series^{[30, 31]} ,i.e.,

where The numerical method given above is a fourth-order formula. By applying a higher-order quadrature formula to Eq. (58),other approximations with higher-order terms for the Magnus series can be obtained. The advantage of the Magnus series method is the preservation of the qualitative properties of the real solutions ^[31] .

According to the property of the transfer matrix,the transfer matrix and its related integration can be expressed as

Therefore,the transfer matrix Φ_kk,0 of the time-varying system can be calculated by Eqs. (63) and (59),and the matrix Ψ_k,ican be calculated from Eqs. (59) and (64) by the Gauss integration formula.

Once the transfer matrix is obtained,the LQ optimal control problem with control inequality constraints can be solved by the numerical method given in Section 4. 6 Implementation and results 6.1 Multilevel implementation of parametric variational algorithm

In the previous sections,the parametric variable method and the corresponding numerical algorithm are given for the LQ optimal control problem with control inequality constraints. However,detailed implementations for practical applications are worth considering. In this paper,a multilevel iteration approach is adopted to improve the efficiency of the numerical method.

The main idea of the multilevel iteration is as follows. The efficiency of solving the linear complementarity problem highly depends on the initial iteration values. Therefore,choosing better initial values is essential. In this paper,the LQ optimal control problem is first solved on a sparse time grid,and then the initial values of the parametric variable multipliers,which are used to solve the linear complementarity problem on dense time grids,are approximated by the parametric variable multipliers on the sparse grid. The details of the implementation are given as follows:

(i) Assume that the fixed time length of the LQ optimal control problem is tf,andthe solutions on the grids with 2Mequal subintervals are required.

(ii) Divide the whole time interval into 2M0 (M0(iii) Select the initial values for the Lemke algorithm,and letm=M0.

(iv) Solve the LQ optimal control problem with control inequality constraints by the parametric variable algorithm proposed in this paper,and obtain the parametric variable multipliers and the state and costate variables.

(v) If the number of grids satisfies the requirement of Step (i),then stop the computation; otherwise,double the time grids,i.e.,divide the whole time interval into 2^{m+1 subintervals with equal length,and letm:= m+1.}

(vi) Map the parametric variable multipliers of the sparse grids (themlevel) onto the dense grids (m+1 level) with the Lagrange interpolation.

(vii) Solve the linear complementarity problem on the dense grids (them+1 level) by the parametric variable multipliers on the dense grids as the initial values of the Lemke algorithm.

(viii) Go to Step (v). For the above adaptive algorithm,when the grids are sparse,the scale of the linear complementarity problem is small. Therefore,it is efficient to solve the linear complementarity problem. When the time grids are refined,the initial values used in the Lemke algorithm are approximated by the results of the sparse grids,which are closer to the analytical solution. Therefore,on the fine grids,the convergencespeed of the Lemke algorithm is much faster. 6.2 Numerical examples

First,two numerical examples with time-invariant and time-varying coefficient matrices are used to test the precision and the efficiency ofthe proposed algorithm. Then,the numerical algorithm is used to solve an optimal control problem of rendezvousing spacecrafts with a finite low thrust.

To test the precision of the proposed algorithm,the relative errors of the state and the control variables are defined as follows:

wherex(t)andu(t) denote the numerical solutions,and x(t)^* and u(t)^* denote the reference and exact solutions,respectively.

For the first two examples,the proposed method is compared with the direct collocation method and the pseudospectral method. In the detailed implementation of the direct collocation method,an explicit Euler scheme and an implicit trapezoidal scheme are used to discretize the state and control variables. The LQ optimal control problem with control inequality constraints is transformed into a standard quadratic programming problem which is solved by the subroutine quadprog of MATLAB. A Radau pseudospectral method ^[32] is also used for the numerical comparisons in this paper. The pseudospectral method is used widely in nonlinear trajectory optimization,and needs the computation of the derivatives of the objective function gradient and the Jacobian matrix for increasing the efficiency of the nonlinear program. In this paper,“pseudospectral method 1” means that the finite differencing method is used to compute the gradient and the Jacobian matrix,and “pseudospectral method 2” denotes that the analytic derivative is used for the gradient and the Jacobian matrix.

Example 1 A one-dimensional time-invariantsystem is considered. The differential equation and the initial condition of the controlled system are

The performance index is where t_f = 1. The control variable is constrained by the following inequality: Because there is no analytic solution for this problem,a reference solution obtained with the indirect method is used for comparison. In the indirect method,the Hamiltonian boundary value equations can be obtained by the maximum principle,and the reference solution can be obtained by solving the Hamiltonian boundary value equations using the MATLAB bvp4c solver with 10^-12 as the absolute and the relative error tolerances.

Figures 1 and 2 give the numerical results for the state,costate,and control variables when 32 intervals are used,which show that theyare very close to the reference solutions. In particular,Fig. 2 shows that the control constraint given in Eq. (68) is satisfied. Furthermore, for different intervals,i.e.,2³,2⁴,···,2¹⁰,the proposed method is compared with the Euler collocation method and the trapezoidal collocation method. The precision and CPU time for the proposed method,the Euler collocation method,the trapezoidal collocation method,and the pseudospectral methods are given in Figs. 3 and 4. It can be seen that the pseudospectral method has the fastest convergence rates among all the numerical methods. However,if the same CPU time is used,the proposed method is more accurate than the Euler collocation method,the trapezoidal collocation method,and the pseudospectral method. To achieve the same precision,the proposed method needs less CPU time than the other methods.

Example 2 In this example,a one-dimensional time-varying system is considered ^{[33, 34]} .

The time-varying differential equation and the initial/terminal conditions of the controlled system are

where The performance index is where the fixed terminal timetf is 10. The following inequality constraint is imposed: For this problem,the exact solutions for the control variable can be given by ^{[36, 37]}

The numerical results computed by the proposed method using 64 equal intervals are given in Figs. 5 and 6,which show that the numerical results of the state,costate,and control variables agree with the exact solutions. Figures 7 and 8 give the efficiency and the precision comparisons among the proposed method,the Euler collocation method,the trapezoidal collocation method,and the pseudospectral method. The conclusions from these two figures are the same as those in Example 1,i.e.,the pseudospectral method has the fastest convergence rates among all the numerical methods. However,if the specific precision or CPU time is given, the proposed method and the pseudospectral methods are more advantageous than the other methods. Especially,the proposed method ismore accurate than the pseudospectral method for control variables.

Example 3 In this example,an optimal control problem for rendezvousing spacecrafts with a finite low thrust is considered. Because theorbits of the spacecrafts may be circular or elliptical,the relative dynamical linearization equation describing the rendezvous can lead to the Clohessy-Wiltshire (C-W) equation for time-invariant systems or the Lawden equation for time-varying systems. Therefore,in the following paragraphs,the optimal control problem is discussed based on these two different kinds of relative dynamical models. The reference coordinate (X,Y,Z) with its origin at the center of the Earth is the inertial coordinate system, and the relative coordinate frame (x,y,z) with its origin on the lead spacecraft is the main coordinate frame for the relative dynamical equation. The x-axis is along the radius from the Earth to the leader spacecraft,they-axis is in the direction of motion,and the z-axis is perpendicular to the orbit plane to complete a right-handed coordinate system.

For the circular reference orbit,the linearization equation of the relative dynamics is the well-known time-invariant C-W equation ^[35] ,which can be expressed in the form of a state space as follows:

wherenis the mean motion frequency of the reference satellite,x,y,andzdenote the relative positions, denote the relative velocities in the x,y,and z-directions,and ux,uy, and u_z are the three components of the thrust acceleration and are taken as the control inputs.

For the elliptical reference orbit,the leader spacecraft follows an elliptical reference trajectory with the Earth’s center at one of its foci. The linearization equation of the relative dynamics is the well-known time-varying Lawden equation ^[36] ,whichcanalsobeexpressedintheformofa state space as follows:

where in which edenotes the eccentricity of the reference orbit of the leader spacecraft. This is a time-varying system in terms of the true anomaly θ.

For both the time-invariant C-W equation and the time-varying Lawden equation,the optimal control problem of rendezvousing spacecrafts is the minimization of the cost expenditure, i.e.,the performance index is selected as

whereTis the rendezvous time.

In this example,the initial state is given as

(5 000 m,−3 000 m,4 000 m,−30 m/s,−10 m/s,20 m/s)^T

, and the final state is given as (0,0,0,0,0,0)^T. Meanwhile,we assume a finite thrust of the spacecraft,which can be described by the following equations: where are the limits of the thrust acceleration in the x-,y-,and zdirections,respectively. To measure the cost expenditure for rendezvousing spacecrafts,the velocity increments are defined as ^[37] First,the velocity increment for different control constraints is considered for both the CW and Lawden equations. The rendezvous timeT is 1 000 s,the length of the semimajor axis is 10 000 km,and the limits of the thrust acceleration in the x-,y-andz-directions are assumed to be the same and are denoted with the symbolu limit (in unit of m·s^-2). The velocity increment ΔV (in unit of m·s^-1) is computed for five different control constraints: u^limit =0.06,0.07,0.08,0.09,infinite,in which “infinite” indicates that there is no constraint used to the control input. To solve this problem,256 intervals with equal length are used,and the results are given in Table 1. Table 1 shows that there is no difference between the velocity increments ΔV for the time-invariant C-W model and the time-varying Lawden model when the orbit is a circular orbit,i.e.,when the eccentricity is zero. From the theoretical analysis, the C-W model is equivalent to the Lawden model when the eccentricity is zero. Hence,the numerical results are consistent with the theoretical analysis,which proves the correctness of the proposed method in certain contexts. Table 1 also shows that for a fixed rendezvous time, the velocity increments increase when the limits on the thrust acceleration u^limit decrease, indicating that the optimal solution obtained by the finite low thrust is the suboptimal solution of the unconstrained optimal spacecraft rendezvous.

Second,the velocity increments for differentrendezvous times are discussed for the timevarying Lawden equation. Three cases with different control constraints u^limit are considered: Case 1,u^limit =0.07 m/s²,Case 2,u^limit =0.08 m/s²,and Case 3,u^limit =0.09 m/s².The eccentricityefor the Lawden model is 0.5,and the other parameters are the same as those given before.

In Fig. 9,the velocity increments ΔV(m·s^-1) for the three types of control constraints are shown with different rendezvous time. The results show that the velocity increments are significantly different before 1 200 seconds,and converge after 1 300 seconds. This phenomenon can be explained as follows. If the rendezvous time is long enough,the optimal controls cannot reach the limitation of the three control constraint types. Therefore,the rendezvousing spacecraft problems corresponding to the three types of control constraints all become unconstrained thrust rendezvous problems,and the control constraints have no influence on the velocity increments. Figure 9 also shows that for fixed rendezvous time,if the constraint of the thrust acceleration is stricter,the velocity increments are larger,and for thesame constraint on the thrust acceleration,the smallestvelocity increments exist for different rendezvous time,i.e.,the A,B,andCpoints given in Fig. 9.

Figures 10 and 11 give the detailed thrust accelerations,the relative positions,and the relative velocities for the rendezvous time of 1 000 seconds and 1 500 seconds,respectively.

Table 2 gives the smallest velocity increments and the rendezvous time for three different control constraints,which show that the smallest velocity increments correspond to different rendezvous time and that the stricter constraints on the thrust acceleration lead to longer rendezvous time corresponding tothe smallest velocity increment.

7 Conclusions

Based on the parametric variational principle,the LQ optimal control problem with control inequality constraints is transformed into the Hamiltonian canonical equations coupled with the linear complementarity equations. The linear complementarity problem is solved by the linear complementarity solver in the discrete time domain. The algorithm proposed in this paper is suitable not only for time-invariant systems but also for time-varying systems. To improve the efficiency of solving the linear complementarity problem,a multilevel iteration idea is proposed in this paper. The numerical examples indicate that the proposed method is effective for the LQ optimal control problem withcontrol inequality constraints. The proposed method is successfully used to solve an optimalcontrol problem of rendezvousing spacecrafts with a finite low thrust.