Shanghai University
Article Information
- Deng-zhe WEN, Yu-shu CHEN. 2014.
- Bifurcation analysis of fan casing under rotating air flow excitation
- Appl. Math. Mech. -Engl. Ed., 35(9): 1099-1114
- http://dx.doi.org/10.1007/s10483-014-1853-6
Article History
- Received 2013-3-6;
- in final form 2014-1-16
Vibration problems are important issues that cannot be ignored in the design of engine development. Fan casing is an important part of engine,whose vibrations directly reflect the vibration level of the engine machine. The structural modes show some geometric nonlinearity with the thin-walled design of modern aviation engine casing. The vibration problems are greatly prominent in the role of incentives under the rotor centrifugal force,air force,and jet noise. The diameter of the fan casing increases with the increase in the bypass ratio,resulting in the reduction of the natural frequency of the structure. The blade tip of the fan rotor achieves a high line speed due to the larger diameter. In addition,as a result of the wide-chord fan rotor blades,the wake casing exciting force increases,resulting in high-frequency travelingwave resonance problems of fan casing. Intensive resonance of fan casing will appear when the natural frequency equals the blade passing frequency [1] .
Aeronautical engine casing vibrations have been of great interest to many domestic and foreign researchers in recent years. The finite element method was used to analyze the reasons for the fan casing vibration [1] which damped the measure of the increasing rectangular crosssectional annular structure damping on an appropriate position in the casing. Xu and Fan [2] introduced a low cycle fatigue life prediction method based on local stress and strain of engine casing for determining the casing load spectrum. Qi and Wen [3] analyzed the laws of the buckling behavior of the outer ducted casing under the axial pressure,end torque,and internal pressure combined effects,and concluded that the combination of axial compression,torque,and internal pressure made the casing buckled. Wu and Qi [4] proved the reasonableness of shell elements in creating thin-walled structures by a model comparison and a test verification method. Su and Sha [5] studied the aeronautical cylindrical shell vibration response problems under noise excitation by a calculation method based on the coupling of the finite element and the boundary element to analyze the vibration response of the thin-walled cylindrical shell structure under the acoustic excitation. Rougui et al. [6] studied the nonlinear free and forced vibrations of the circular thin shell structure with simply supported coordinates. Chai and Qiu [7] established the stress intensity factor calculation methods of the structures of plate,cylindrical,and round shell crack. Zhu et al. [8] studied the variations of the stress intensity factor and critical crack length of the surface oblique crack on a round tube. The above researches of the casing vibration and crack were carried out by either numerical or experimental methods.
In this paper,the vibration problems of aero-engine fan casing under rotating airflow excitation are studied by the theoretical analysis methods. The fan casing model is reasonably investigated based on the geometric characteristics of aero-engine fan casing. In addition,a singularity analysis of the bifurcation equations and the dynamic reasons of casing cracks during the hysteresis interval are studied. The research proposed in this paper provides a theoretical basis for fan casing design and system parameter optimization. 2 Establishment of model
In modern aero-engine design,casing (fan casing) is often designed to be thin in order to
reduce the weight and improve the thrust-weight ratio. Shell elements can simulate the casing
structure when the thickness-diameter ratio is in the range of 0.014<
 <0.037
[4]
.The
front-end of fan casing to the intermediate casing can be simplified as a circular thin shell
structure according to the structural characteristics of the aero-engine,(see Fig. 1)
[9]
.Figure 2
demonstrates the rotating air flow excitation. According to Kirchhoff’s thin plate theory
[10]
,
we make the following assumptions:
<0.037
[4]
.The
front-end of fan casing to the intermediate casing can be simplified as a circular thin shell
structure according to the structural characteristics of the aero-engine,(see Fig. 1)
[9]
.Figure 2
demonstrates the rotating air flow excitation. According to Kirchhoff’s thin plate theory
[10]
,
we make the following assumptions:
 |
| Fig. 1 Dynamics model of fan casing |
 |
| Fig. 2 Rotating airflow incentive schematic diagram |
(i) The straight line perpendicular to the middle plane before deformation is still straight with the same length after deformation.
(ii) Compared with the stress perpendicular to the middle plane direction,the stresses in other directions can be negligible. 3 Dynamical equations of fan casing
As shown in Fig. 1,a curvilinear coordinate system Oxθz is introduced,and L,R,andh represent the length,the radius,and the thickness of the casing shell,respectively. The origin Ois fixed on the center of the free end of the shell,xis taken along the axial direction of the case shell,andθandz are along the circumferential and radial directions of the case shell, respectively. u,v,andwdenote the displacements of any point in the case shell with respect to thex-,θ-,andz-directions,respectively,andwis taken to be positive outwards.
Assume that the strains on the middle surface are ε(0) x ,ε(0)θ ,and γ(0)xθ ,respectively,according to the general shell theory,the changes in the curvatures of the middle surface are κ1 and κ2, and the torsion of the middle surface isχ. Then,we have
According to the nonlinear theory of thin shell,we have The stress-strain relationship can be expressed as whereEis Young’s modulus of elasticity,and μis Poisson’s ratio.According to the classical assumption of plane stress [11] ,the elastic strain energy of the casing shell with the thicknesshcan be expressed as follows:
The kinetic energy of the casing shell can be described asFor fan casing,the main external excitation is the rotating air flow excitation [12] ,whichcan be expressed as
wherefkis the amplitude of excitation,Ωkrepresents the frequency of the excitation,δis the Dirac delta function,andkis the number of harmonics of the load.According to Hamilton’s principle,we have
where Substituting (4),(5),and (8) into (7),from (6),we have whereρdenotes the density of the shell,cis the damping coefficient,Nx,Nθ,andNxθrepresent the stress resultants,andMx,Mθ,andMxθrepresent the moment resultants,which are defined bySubstituting (1),(2),and (3) into (10a) and (10b),and then substituting (10a) and (10b) into (9a)-(9c),we have
whereKandDare the flexural rigidities of the shell expressed by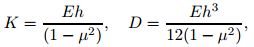
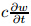 denotes the damping of the system.
3.1 Combination method of beam function
denotes the damping of the system.
3.1 Combination method of beam functionAs shown in Ref. [13] (see Fig. 3),where Ω1 and Ω2 denote the natural frequencies of the vibrations of the beam and the housing,the results of the beam theory and the shell theory are fairly close for L/(mR)>8. Therefore,the vibration problems of circular shell can be studied by the beam theory.
 |
| Fig. 3Combination method of beam function [13] |
The combination method of axial beam functions and circumferential trigonometric functions is used to approximate the cylindrical shell vibration function [14] .
whereu(t),v(t),and w(t) are the vibration amplitudes in the directions ofx,θ,andz,respectively, Φk(x) is the axial wave function satisfying the boundary conditions,andnrepresents the number of the circumferential waves.The axial wave function is
For the clamped-freeform casing system,the initial conditions are
Substituting (14) and (15) into (13),we have whereFigure 4 shows the vibration mode of Φk(x),wheremdenotes the number of the axial half wave.
 |
| Fig. 4 Modes of casing bending vibrations withm=1, 2, 3, 4andn=0 |
The modes of beam vibration withm=1,2,3,4andthemodesofcircumferential vibration withn=0,1,2,3,4 are shown in Fig 5.
 |
| Fig. 5 Modes of casing bending vibration withm=1, 2, 3, 4andn=0,1,2,3,4 |
The dimensionless expressions of the parameters in (11a)-(11c) are
Substituting (18) into (11a)-(11c),from (12) and (16),we obtain
whereai,bi ,andci (i=1,2,3) are shown in Appendix A. 3.2 Effects of geometric parameters of system on natural frequency The effects of the geometric parameters and circumferential vibration on the natural frequency of the casing system are discussed. Supposeu(t)=Acos(Ωt),v(t)=Bcos(Ωt),and w(t)=Ccos(Ωt). Substituting the above equations into (19) yieldsConsidering the linear portion of (20) and letting the coefficient matrix equal to zero yield
where From Figs. 6-8,we can draw the conclusions that the natural frequency of the system is significantly affected by the radius-length ratio,the thickness-radius ratio,and the circumferential wave numbers. The natural frequency of the system increases with the increases in the radius and the length ratio (see Fig. 6). The natural frequency of the system increases with the increase in the wave number (see Fig. 7). The natural frequency of the system increases with the increase in the thickness-radius ratio (see Fig. 8).  |
| Fig. 6 Effects of geometric parameter on natural frequency of shell |
 |
| Fig. 7 Effects of radius-length ratio and wavenumber on natural frequency of shell |
 |
| Fig. 8 Effects of thickness-radius ratio and circumferential wave number on natural frequency of shell |
Ignoring all inertia terms inubased on the researches given in Refs. [15, 16],we have
After decoupling (23),we get wherek1,k2,k3,k4,f1,f2,α1,α2,andζare shown in Appendix B,andεis a dimensionless small parameter [17] . The natural frequencies ofvandware expressed as follows: Let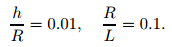
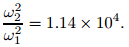
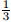 subharmonic resonance and 3 times super harmonic
resonance.
subharmonic resonance and 3 times super harmonic
resonance.
Set
where Tn=εnt.Substituting (26) and (27) into (24) yields
where c.c. is the complex conjugate term. Then,we have andAccording to the condition of eliminating the secular terms,we have
The amplitude and the phase of the first-order approximate solution satisfy the following relations: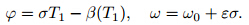
Suppose
Set whereλis the bifurcation parameter,and ε1 and ε2 are the unfolding parameters [18, 19, 20] .Set B2=B. Then,we have
Solving (35)-(38),we can obtain the transition sets (see Fig. 9).From Fig. 9,we can find that the parameter space of the transition sets is divided into three regions,i.e.,Region (1),Region (2),and Region (3). The amplitude-frequency vibration curves of the three regions are shown in Fig. 10. The bifurcation diagram of the three regions are shown in Fig. 11.
From the diagram shown in Fig. 11,we know that the phenomenon of bifurcation appears from Region (1) to Region (2),and the hysteresis appears from Region (2) to Region (3) [21, 22] . Bifurcation or suddenly jump will appear with the casing vibrations when unfolding parameters are selected in Region (1) or Region (3). Then,the stability of the casing system might be affected by the bifurcation and hysteresis. Therefore,the parameters should be prevented from appearing in this area,and the bifurcation parameters should be selected from Region (2).
 |
| Fig. 9 Transition sets: (a) bifurcation set; (b) hysteresis set |
 |
| Fig. 10 Amplitude-frequency curve of vibration |
 |
| Fig. 11 Bifurcation diagrams of Regions (1)–(3) |
Letfmbe the vibration frequency (Hz),nbe the rotational speed of the fan rotor (r·min-1), andmbe the multiple number. Then,according to the multiple relationship [1] ,we have
The physical parameters of the fan casing are listed in Table 1.According to the traveling wave vibration theory[12] ,the casing shell will exhibit the former traveling wave resonance with the same frequency in the radial direction when the harmonics number of the rotary pulse excitation isk. Substituting the data in Table 1 into (39),we get m= 18,which is the same as that obtained with the fan blades. Therefore,we obtain that the casing vibration is a traveling wave vibration aroused by the rotor blade rotating exciting force.
The physical parameters of the casing are as follows:
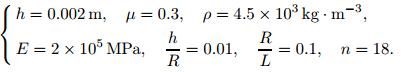
We can get the dimensionless frequency by calculating
From (18),we can get the relationship between the vibration frequency of the casing. The dimensionless frequency can be obtained as follows:
From Fig. 10,we obtain that the jumping of the system appears over the region 1.25Ω2− 1.5Ω2. Substituting the physical parameters into (40) and (41),we can get that the range of the system vibration frequencyΩwith jumping is 3 125 Hz-3 750 Hz. By (39),we get that the range of the fan speednwith jumping is 10 416 r·min-1-12 500 r·min-1. 5.2 Possibility analysis of cracking during hysteresis interval The inner tiny structure of the casing material exists unavoidable defect. It is a multi-crack or micro-crack medium. The stress concentration will appear in the crack tip,resulting in crack propagation until the casing is destructed,when the casing is subjected to rotating airflow force. According to the theory of fracture mechanics,the crack will appear when the stress intensity factor of the material is greater than the critical stress intensity factor.
Let KIII denote the stress intensity factor and KCdenote the critical stress intensity factor. Then,the criterion of craze is KIII> KC.
As shown in Fig. 12,the relationship of the stress intensity factor and displacement of the III crack [23] is
 |
| Fig. 12 Ripped-type (III type) schematic |
From the above equation,we can obtain that the stress intensity factor increases as the displacement increases,and when it reaches or exceeds the critical stress intensity,cracks will appear.
The relationship of the critical stress intensity factor and the fracture toughness is shown in Fig. 13 [24] ,where K'III=dΔ/dt denotes the excitation frequency,and the fracture-resistance has the minimum when the frequency is 103Hz. With the results obtained in the hysteresis interval,we can obtain that the range of the frequencyΩis 3 125 Hz-3 750 Hz at a high incidence of craze.
 |
| Fig. 13 Relationship of critical stress intensity diagram of crack factor and fracture toughness |
From the above comprehensive analysis,we can see that the stress intensity factor increases with the increase in the amplitude,but the critical stress intensity factor has a minimum value. Accordingly,the criterion for cracking,KIII ≥ KC,is extremely easy to be satisfied. The possibility of casing crazes greatly increases during the hysteresis interval. 6 Conclusions
In this paper,based on the geometric features of the aero-engine fan casing,a cantilever casing model is constructed. The dynamic equations of fan casing are established by using Donnelly’s shell theory and Hamilton’s principle,and then the dynamic behaviors are investigated by using the multiple-scale method.
The effects of the geometric parameters and circumferential wave numbers on the natural frequency of the system are studied. The natural frequency of the system increases with the increases in the radius,the length ratio,the wave number,and the thickness-radius ratio.
The bifurcation characteristics of the system are analyzed based on the singularity theory. We find that bifurcation modes vary in different regions. Bifurcation or suddenly jump will appear when unfolding parameters are selected in Region (1) or (3). The stability of the casing system might be affected in these regions. Therefore,the bifurcation parameters should be avoided appearing in these regions and should be selected from Region (2).
There will be a sudden jump phenomenon when high-frequency vibrations occur. According to the existing data analysis,we can get that the frequency jump intervals and fan speed intervals of the casing vibrations are 3 125 rad·s-1-3 750 rad·s-1and 10 416 r·min-1 -12 500 r·min-1. During the hysteresis interval,as the amplitude increases as well as the critical intensity factor decreases,the possibility of casing craze greatly increases. The engine should be avoided working too long in this interval. The analysis in this paper has theoretical significance for the design and control of fan casing. Appendix A
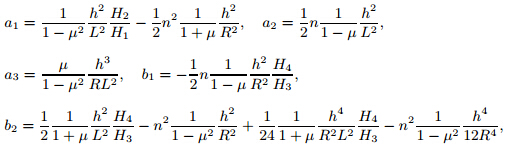
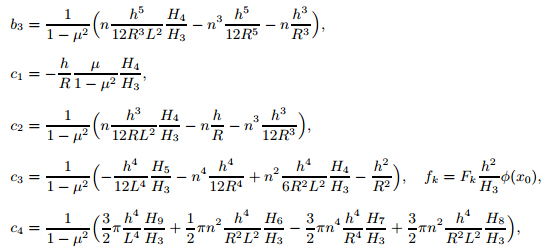
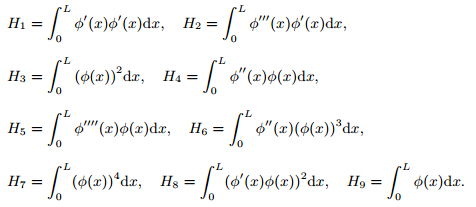
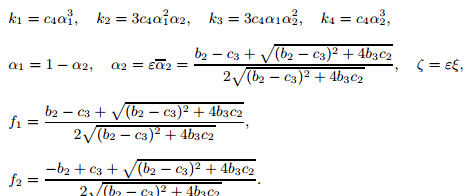
| [1] | Cai, X. X., Xiao, X. H., Wang, T., and Wu, Z. Q. Optimization design of a fan casing for reducing vibration. Journal of Aerospace Power, 25(2), 396-401 (2010) |
| [2] | Xu, T. and Fan, Y. H. Prediction of low cycle fatigue life of engine casing. Journal of Nanjing Aeronautical Institute, 22(2), 1-9 (1990) |
| [3] | Qi, H. Y. and Wen, W. D. Numerical analysis of structural stability of the composite case under complicated loads. Aeronautical Manufacturing Technology, 32(7), 35-38 (2003) |
| [4] | Wu, Y. D. and Qi, W. K.Modal analysis and model verification of an aeroengine casing. Mechanical Science and Technology for Aerospace Engineering, 29(11), 1487-1492 (2010) |
| [5] | Su, Z. M. and Sha, Y. D. Thin Air Shell Structure Vibration Response in the Sonic Excitation (in Chinese), M. Sc. dissertation, Shenyang Aerospace University, 27-49 (2007) |
| [6] | Rougui, M., Moussaoui, F., and Benamar, R. Geometrically non-linear free and forced vibrations of simply supported circular cylindrical shells: a semi-analytical approach. International Journal of Non-Linear Mechanics, 42(8), 1102-1115 (2007) |
| [7] | Chen, Y. Q. Analysisand Researchof Stress Intensity Factor for Cylinder Surface Elliptical Crack by Means of Finite Element Method (in Chinese), M. Sc. dissertation, Wuhan Institute of Technology, 59-88 (2006) |
| [8] | Zhu, M. Y., Li, C., and Tie, Y. Simulation of stress intensity factors and critical crack length of surface oblique crack on round tube. Transactions of the Chinese Society for Agricultural Machinery, 41(7), 210-222 (2010) |
| [9] | Xiao, G. S. Aircraft Engine Design Manual Book 5 Vortex Spray and Turbofan Engine Overall, Aviation Industry Press, Beijing, 272-273 (2001) |
| [10] | Yan, L. T. Structural System Dynamic Analysis, Beijing University of Aeronautics & Astronautics Press, Beijing, 126-130 (1989) |
| [11] | Nayfeh, A. H. and Mook, D. T. Nonlinear Oscillations, Wiley, New York, 100-117 (1979) |
| [12] | Wang, G. H. and Li, L. Method for traveling wave vibration analysis of fan casing in aero engine. Journal of Aerospace Power, 15(2), 183-186 (2000) |
| [13] | Cao, Z. Y. Vibration Theory of Plates and Shells, China Railway Publishing House, Beijing, 272-276 (1989) |
| [14] | Yan, L. T. Study on travelling wave vibration of bladed disks in turbomachinery. Journal of Aerospace Power, 5(1), 35-39 (1990) |
| [15] | Bhimaraddi, A. Large amplitude vibrations of imperfect antisymmetric angle-ply laminated plates. Journal of Sound and Vibration, 16(2), 457-470 (1999) |
| [16] | Nosir, A. and Reddy, J. N. A study of nonlinear dynamic equations of higher-order deformation plate theories. International Journal of Non-Linear Mechanics, 2(6), 233-249 (1991) |
| [17] | Liu, Y. Z. and Chen, L. Q. Nonlinear Vibration, Higher Education Press, Beijing, 63-65 (2001) |
| [18] | Qin, Z. H. Singularity Method for Nonlinear Dynamical Analysis of Systems with Two Parameters and Its Application in Engineering (in Chinese), Ph. D. dissertation, Harbin Institute of Technology, 47-56 (2010) |
| [19] | Chen, Y. S. Nonlinear Vibrations, Higher Education Press, Beijing, 237-250 (2002) |
| [20] | Chen, Y. S. Bifurcation and Chaos Theory of Nonlinear Vibration System, Higher Education Press, Beijing, 120-148 (1993) |
| [21] | Qin, Z. H., Chen, Y. S., and Li, J. Singular analysis of a two-dimensional elastic cable with 1:1 internal resonance. Applied Mathematics and Mechanics (English Edition), 31(2), 134-142 (2010) DOI 10.1007/s10483-010-0202-z |
| [22] | Chen, Y. S., Yang, C. X., Wu, Z. Q., and Chen, F. Q. 1:2 internal resonance of coupled dynamic system with quadratic and cubic nonlinearities. Applied Mathematics and Mechanics (English Edition), 22(8), 817-842 (2001) DOI 10.1023/A:1016342326645 |
| [23] | Chai, C. J. and Qiu, Y. Y. Simulation on the Cylinder Expanding Processing and Research of the Creak Generation Mechanism (in Chinese), M. Sc. dissertation, Xidian University, 89-140 (2010) |
| [24] | Fan, T. Y. Fracture Theory Basis, Science Press, Beijing, 322-326 (2003) |
 2014, Vol. 35
2014, Vol. 35








































