2014, Vol. 35
Shanghai University
Article Information
- Tian-tian MA, Chang-fu WEI, Pan CHEN, Hou-zhen WEI. 2014.
- Implicit Scheme for integrating constitutive model of unsaturated soils with coupling hydraulic and mechanical behavior
- Appl. Math. Mech. -Engl. Ed., 35(9): 1129-1154
- http://dx.doi.org/10.1007/s10483-014-1859-6
Article History
- Received 2013-9-24;
- in final form 2014-1-16
2 College of Civil and Architectural Engineering, Guilin University of Technology, Guilin 541004, Guangxi Province, P. R. China
Unsaturated soils are three-phasic porous media,which consist of solid matrixes with interconnected pores saturated by water and air. In general hydraulic and mechanical processes, complicated physic-chemical interactions may occur among the three bulk phases in the unsaturated soils through the interfaces separating the bulk phases. These interactions can significantly influence the mechanical behavior of a soil,and thus complicate the solution of the global differential equations governing the coupling processes in the unsaturated soil. There are three interfaces in an unsaturated soil,separating solid matrix-pore water,pore water-pore air, and solid matrix-pore gas,respectively. The water-gas interface maintains a difference between the pore air pressure and the pore water pressure. This pressure difference (usually termed as “matric suction”) depends upon the degree of saturation or moisture content and the wetting/ drying history,which describes the soil-water characteristics[1]. It has been well recognized that the soil-water characteristic curve of an unsaturated soil is hysteretic in nature[2,3].
One of the major differences between a fully saturated soil and its unsaturated counterpart resides in the fact that the latter depends not only on the stress history but also on the hydraulic history of the soil. The effect of the stress history has been very well described in modeling the constitutive behavior of fully saturated soils. In contrast,however,little effort has been made to address the effect of the hydraulic history in unsaturated soil modeling. It has been found that the local pattern of the moisture distribution in an unsaturated soil depends largely upon its previous wetting/drying path,resulting in the hydraulic history-dependence of the unsaturated soil behavior[4]. It has been shown that the capillary hysteresis phenomenon is associated with the intrinsic dissipation processes related to the internal structural rearrangements of unsaturated soils,which can be characterized by using a series of internal state variables[5,6,7]. Based on this,Li[7] has recently developed a theoretical framework,by which the capillary hysteresis and skeletal deformation can be consistently addressed in a fully-coupled manner.
Within this context,a new constitutive model for unsaturated soils has been recently developed, which can simulate plastic deformation and capillary hysteresis in a coupling and hierarchical way[8]. It is remarkable that in the new model,the role of the soil-water characteristic curve (SWCC) is two-folded,i.e.,while being used to describe the capillary hysteresis, the SWCC is also introduced to characterize the effect of the hydraulic history on the mechanical behavior. The performance and experimental validation have been described in Ref. [8]. In this paper,we shall develop an implicit Scheme to integrate the proposed model,through which the new model is numerically implemented into a finite element code for analyzing the boundary-value problems related to unsaturated soils.
In general,a constitutive model of unsaturated soils includes two major components,describing the stress-strain relationship and the soil-water characteristics,respectively. These two constitutive components are represented in an uncoupled[9,10] or coupled[11,12] manner. Vaunat et al.[13] developed an implicit integration Scheme for the Barcelona basic model[9] based on the return-mapping algorithm[14] with a mixed control constitutive driver,where an extra strain component specially associated with the suction variable was used as an additional control variable and the integration process was driven by both strains and stresses. Macari et al.[15] developed a similar integration Scheme. Zhang et al.[16] integrated the constitutive model of unsaturated soils proposed by Bolzon et al.[10] by generalizing Simo and Taylor’s algorithm[17]. Basically,these integration procedures are similar to those for saturated soils. In these procedures, however,special treatment is needed for the variables related to the matric suction,e.g., the rate of the matric suction is assumed vanishing in dealing with the consistency condition.
To preserve the consistency,the matric suction can be treated as a strain variable instead of a stress variable. Sheng et al.[18] developed a complete finite-element procedure based on the suction-hardening constitutive model,treating the matric suction as an additional strain variable. The global finite element equations were derived in terms of the displacement and the pore water pressure,and an explicit,strain-driven Scheme was used to integrate the constitutive relation at the Gaussian point. In this approach,however,the pore air pressure was assumed to equal the atmospheric pressure. Zienkiewicz et al.[19,20] developed a static/dynamic theoretical model to analyze the coupling problems of seepage and deformation quantitatively,neglecting the effect of the pore air pressure. Laloui et al.[21] developed the solid-liquid-gas coupling model and the solid-liquid model for porous media,respectively,based on the thermodynamics theory. They pointed out that ignoring the influence of the pore air pressure would cause an inaccurate result. But this model does not consider the plastic yielding. Li et al.[22] and Schrefler and Zhan[23] generalized the theoretical model of Zienkiewicz[19,20] to simulate two-phase flow and deformation problems. Olivella et al.[24] and Thomas and He[25] developed a hydromechanical- thermal coupling approach to simulate the unsaturated soil behavior. Nowamooz et al.[26] developed an elastoplastic constitutive model of unsaturated expansive soils based on the experimental observation. This model was implemented into the finite-element code to analyze the sedimentation of shallow foundation. Simoni et al.[27] investigated the elastoplastic sedimentation during the exploitation of gas reservoirs with and without capillary effects, respectively. They pointed that the capillary effects should be accounted for the ongoing subsidence after the well shutdown. However,these models do not consider the coupling effect of the capillary hysteresis and elastoplastic deformation.
To address the effect of the capillary hysteresis on the mechanical behavior of unsaturated soils,the stress-strain relationship and the soil-water characteristic curve must be formulated in a fully coupled manner[11,12]. Thus far,however,little effort has been made to implement these advanced unsaturated soil models into finite-element codes.
In this paper,a recently developed fully-coupled constitutive model of unsaturated soils is introduced,and an implicit integration Scheme is proposed to implement the new model into the finite-element code U-DYSAC2[28]. The matric suction is treated as an additional strain variable so that the integration process of the constitutive equations is purely strain-driven. The consistent elastoplastic tangent modulus is derived. The standard sign convention in continuum mechanics is adopted in the following context,i.e.,the tensile stresses are positive whereas the compressive stresses are negative. 2 Theoretical formulation
For completeness,the fully-coupled constitutive equations are briefly introduced in this section. The detailed description of the constitutive model can be found in Ref. [8]. The effective stress σij and the suction Sc are adopted as the stress state variables in the model, which are work-conjugated to the strain εij and the degree of saturation Sr,respectively[29]. In such an approach,both unsaturated and saturated soil behaviors are described in a consistent way. To remain clarity,the apostrophe in the superScript of the effective stresses is omitted hereinafter. The mean and deviatoric stresses are defined,respectively,as follows:
where σij = (σijT− pgδij) + Sr(pg − pl)δij. δij is the Kronecker delta. σijT is the total stress. pg and pl are the pore air and pore water pressure,respectively. Sr is the saturation degree. Sc is the matric suction,i.e.,sc = pg − pl. In this paper,the matric suction is equal to the capillary suction,and the osmosis effect is excluded. 2.1 Stress-strain relationship
The stress-strain relationship is developed by generalizing the modified Cam-clay model[30], in which the yield function is given by
where M is the slope of the critical state line,which is assumed to be constant for various saturations. pc is the preconsolidation pressure. The yield surface is Schematically shown in Fig. 1.
 |
| Fig. 1 Yield surface of new constitutive model |
At full saturation,pc is a function of the plastic volumetric strain only,i.e.,pc = pc0(εvp ). Under partially saturated conditions,pc depends upon the matric suction,the degree of saturation, and the plastic volumetric strain. It is suggested herein that
where h is a correction function,which accounts for the hardening effect of unsaturation. As discussed in the previous section,h is assumed as a function of Sc,Sr,and the plastic volumetric strain εvp .
Because the quantity of the meniScus water rings can be represented by the amount of the pore air,we suggest that the hardening effect of unsaturation can be collectively characterized by the variable (1 − Sr)Sc. Remarkably,at the specified matric suction,the value of (1 − Sr)Sc depends uniquely upon the pattern of the moisture distribution in the pores,i.e.,upon the hydraulic history that the soil experiences. It is proposed herein that
where r is a parameter which truncates the effect of the high matric suction on the preconsolidation pressures,i.e.,r = h|Sc→∞. m is a factor characterizing the changing rate of the preconsolidation pressure with the variation of (1 − Sr)Sc. εvmaxp is the threshold value of the plastic volumetric strain at which the effect of unsaturation becomes trivial. Sirr r is the residual degree of saturation. <>is the Macauley bracket,which is defined as
When the stress state remains on the yield surface,the following condition will be satisfied:
The hardening parameter is given in a rate form as follows: The incremental stress-strain relation can be written as where dσ is the incremental stress tensor,and dε is the incremental total strain. dε can be additively decomposed into an elastic part dεe and a plastic part dεp,i.e.,dε = dεe +dεp. De is the elastic stiffness matrix given by where K and G are the elastic bulk and shear modulus,respectively,which are defined by
μ is the Poisson ratio. I is the fourth-order unit tensor,i.e.,Iijkl = 1/ 2 (δikδjl + δilδjk). 1 is the second-order unit tensor,and (1 ⊕ 1)ijkl = δijδkl. 2.3 SWCC
In addition to the stress-train relationship,a relationship between the suction and the degree of saturation is required to complete the description of unsaturated soil behaviors. Wei and Dewoolkar[5] proposed a thermodynamically-consistent model for the capillary hysteresis in partially saturated porous media. With some modifications,this model can address the effect of the volumetric strain on the soil-water characteristics. To this end,we first note that
where Vw,Vv,and V are the water volume,the pore volume,and the total volume of the representative element,respectively. The first item of the right-hand side represents the change in the degree of the saturation under the constant-Vv condition,i.e.,only due to the change in the amount of the pore water,while the second item represents the contribution from the change of the volumetric strain. Neglecting the effect of the elastic deformation,we can cast Eq. (12) into where n is the porosity.
According to Wei and Dewoolkar[5],the first term of the right-hand side of Eq. (13) can be described by
where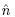
denotes the hydraulic loading direction,and its value is 1 or −1,denoting drying or
wetting. Kp is the negative slope of the current soil-water characteristic curve.
Feng and Fredlund’s model[32] is adopted to describe the main boundaries of the SWCC, i.e.,
where bk and dk are the positive material parameters with different values for wetting and drying,respectively. Ignore the effects of the elastic volumetric strains and the shear strains. Then,bk and dk depend on the plastic volume strain εvp . For simplicity,we propose that where bk0,dk0,and αk (k = DR,WT) are curving-fitting parameters.
Kp is a function of εvp
,Sc,Sr,and 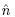. It is given by
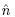) is the negative slope of the corresponding main boundary,which is the main
drying boundary if 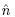= 1 or the main wetting boundary if 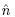= −1. c is a positive material
parameter which is used to describe the discanning behavior. It is assumed for simplicity that
c is a constant,independent of the skeletal deformation. Sc(εvp
,Sr,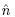) is the suction value
on the corresponding main boundary curve,i.e.,Sc(εvp
,Sr,1) = κDR(εvp
,Sr) for drying and
Sc(εvp
,Sr,−1) = κWT(εvp
,Sr) for wetting,where κDR(εvp
,Sr) and κWT(εvp
,Sr) describe the
main drying and wetting boundaries,respectively. r(εvp
,Sr) is the current size of the bounding
zone,i.e.,r(εvp
,Sr) = κDR(εvp
,Sr) − κWT(εvp
,Sr).
The constitutive model introduced above describes simultaneously the effects of the capillary hysteresis on the stress-strain behavior and the effects of the plastic volumetric strains on the water retention behavior in a coupled manner. A comparison of the simulation results with the experimental results shows that the model can capture the main features of the unsaturated soil behavior,such as swelling or collapse compression during wetting,irreversible compression during drying,and the effect of wetting-drying cycles on the subsequent behavior. 3 Stress-point integration Scheme 3.1 Closest point return-mapping algorithm
The new constitutive model describes the stress-strain relation and water retention characteristic relation in a fully-coupled manner. To integrate the model,the two constitutive equations have to be solved simultaneously. To this end,the matric suction is treated as an additional strain component,and then the rate constitutive equations can be integrated in a way similar to those for saturated soils. The algorithm is consistent with the conventional displacement finite-element method,where the displacements of the skeleton and pore pressures are taken as primary unknowns. Here,the implicit integration algorithm proposed by Borja[33] for the modified Cam-clay model,i.e.,the closest point projection method,is generalized to integrate the combined two relations.
The closest point projection Scheme is the generalization of the backward Euler method, which has been extensively applied to integrate the constitutive model with an arbitrary convex yield surface. This Scheme was first developed by Simo and Taylor[17],and later used to the Cam-clay model proposed by Borja[33]. The Newton-Raphson iteration is used to solve the discrete incremental equations. This integration algorithm is composed of an elastic predictor and a plastic corrector (i.e., return mapping). It is unconditionally stable. Because the change of the pore ratio e is usually small during a load step,it can be treated explicitly and updated at the step n + 1. We define the strain and suction increments,respectively,as follows:
which can be determined by solving the global finite-element method (FEM) equations. 3.1.1 Elastic prediction
Assume that the given strain increment is purely elastic. The trial stresses can be computed as follows:
where σn,εn,and Sc,n are the converged stress,strain,and suction at the previous time step, respectively.
Consider the trial stress invariants,i.e.,the trial mean effective stress and the deviatoric stress,given by
where n is a unit tensor in the radial direction of ξn+1tr. The derivatives of pn+1tr,qn+1tr,and n with respect to εn+1 are where Substitute the trial stresses into the yield function (i.e.,Eq. (2)),and calculate If f1 < 0,the trial stress state is inside the current yield surface. Then,no plastic yielding will occur,and the stress state with the trial stress can be updated as σn+1 = σn+1tr. The incremental capillary hysteresis relation is solved for the saturation degree at the step n+1 by a local Newton iteration on the nonlinear equation The solution procedure for the local Newton-Raphson iteration for Sr,n+1 is as follows:
(i) Let k = 0 and Sr,n+10 = Sr,n.
(ii) Compute f2
(iii) Compute
(iv) If
exits; else,let k := k + 1,and go to Step (ii).
If f1 ≥ 0,the plastic yielding occurs,then go to the next step. 3.1.2 Plastic correction
Treat the capillary hysteresis in a way similar to the plastic deformation. Then,one has to solve the following two equations simultaneously:
To derive an explicit expression for the function f1(Δεvp ,ΔSr),one first note that the return mapping stress tensor can be expressed as It follows that where Δεvp = tr(Δεp),and Δγp = Δεp − 1/ 3Δεvp 1.
Assume that ξn+1tr,ξn+1,and Δγp have the same direction,i.e.,
Adopting the associated flow rule,one can obtain the true stresses as follows: where Δλ is the plastic multiplier in an incremental form.
With Eq. (28),Eq. (23) can be linearized into the following forms:
or in a compact form: (D')(Δε') = (−F),where {Δε'} = {Δλ,ΔSr}. Solving the above equation,one can obtain Δλ and ΔSr. The solution procedure for the local Newton-Raphson iteration for computing the zero of {F} is as follows:
(i) Let k = 0 and {ε'}k = 0.
(ii) Compute {F}k = {F(ε')} .
(iii) If {|Fk|}<{FTOL} ,exits; else,let {ε'}k+1 = {ε'}k − {Fk}· [D']-1 ,k := k + 1,and go to Step (ii).
At each iteration step,update all the related variables until the solution is convergent. 3.2 Consistent tangent modulus
The consistent tangent modulus at the time t + Δt is derived through the exact liberalization of the incremental stress-strain relation,which is consistent with the closest point return-mapping algorithm. Simo and Taylor[34] had shown that the iterative solution Scheme can asymptotically preserve the quadratic convergence of Newton’s methods only when the consistent tangent modulus is introduced.
As shown by Aravas[35],all the partial derivatives can be expressed analytically by decomposing the stress increments into hydrostatic and deviatoric components. It is noted that
Hence,by its very definition,the consistent tangent modulus can be calculated as Using Eqs. (21),(22),(25),and (26),one can obtain the consistent tangent modulus as follows: where
The matrix is generally asymmetric since K(a2b2) is not equal to 2G
(a6b1). It is noteworthy
that when the plastic multiplier Δλ → 0,the above consistent tangent modulus can
degenerate to the continuum tangent modulus.
3.3 Model performance
The suction-controlled triaxial compression tests conducted by Sun et al.[12] on the Pearl clay are used to assess the performance of the coupling constitutive model and the integration Scheme. The stress paths adopted in these experiments are illustrated in Fig. 2. The experimental results are given in Figs. 3 and 4 for the path ABE and the path ABCD,respectively.
 |
| Fig. 2 Stress paths used in triaxial tests where pnet = 196 kPa |
Figures 3(a) and 3(b) depict the relations among σ1/σ3,ε1,ε3,and εv and the relation between σ1/σ3 and the saturation degree,respectively. For the stress path ABE,in the early stage of shearing,the model predicts that the specimen remains in the elastic domain (see the initial vertical line segment in Fig. 3(b)). It is noted that the effect of the elastic volumetric strain on the degree of saturation has been neglected. From Fig. 3,it is clear that the model yields good results.
 |
| Fig. 3 Simulated and measured[12] results of triaxial tests with stress path ABE |
Figure 4(a) shows that the model simulations agree well with the experimental data. From Fig. 4(b),it can be seen that,during the wetting process (from B to C),the model predicts full saturation at the point C,which is inconsistent with the measurement. This discrepancy is due to the effect of the air entrapment in the experiment,which is also responsible for the discrepancy between the predicted and measured strains (see Fig. 4(a)). Remarkably,the saturation degree increases during the shearing process,and this feature has been well captured by the proposed model (see Figs. 3(b) and 4(b)). From these figures,it can be seen that the coupling constitutive model can capture well the features of the unsaturated soil behavior.
 |
| Fig. 4 Simulated and measured[12] results of triaxial tests with stress path ABCD |
It is assumed in the following context that the soils are under the isothermal condition and no chemical reaction or mass exchange between the phases occurs. The equations governing the coupled hydro-mechanical processes include the mass balance equations and the linear momentum balance equations.
The macroScopic balance equations[36,37] are introduced here. The rigorous volume average techniques[38,39] are used to identity the macroScopic quantities representing the microcosmic quantities. 4.1 Mass conservation
The mass balance equations for each phase can be written as
where α =s,l,g represent the solid,liquid,and gas phases,respectively. nα,ρα,and vα express the volume fraction,the true mass density,and the velocity of the α-phase,respectively, satisfying
Ds(*)/ Dt and Df (*)/ Dt are the material derivatives related to the solid skeleton and the fluid motion, which satisfy
where f =l,g.
The Darcy flow velocity of the fluid is defined as
where Uf is the displacement for both fluid phases (liquid and gas).
The volume fraction of the liquid phase n1 is assumed to be a function of the suction and volume deformation of the solid skeleton due to the coupling effect described previously. Then, we have
where usi is the displacement of the solid phase,and the symbol with the Script i,i represents the variable divergence. Incorporating the mass balance equation for the solid phase into the mass balance equations for the liquid phase and the gas phase,respectively,combined with Eq. (37),yields where
K1 and Kg represent the bulk modulus of liquid and air,respectively,and
The spatial variations of the densities of pore fluids ρf ,i can be omitted in general. In these equations,solid phase is incompressible,bulk modulus of liquid is constant,and gas is ideal. 4.2 Linear momentum balance equations
The momentum balance equations for the mixture,liquid phase,and gas phase are used to describe the motion of the unsaturated soil system,where the momentum balance equations for the fluids are the generalized Darcy’s law essentially. Based on the porous medium mechanical theory,the linear momentum conservation equations for pore fluids and mixture can be obtained as follows:
where b is the external supply of the linear momentum,which is the acceleration of gravity g in general (or centrifugal acceleration in the centrifugal test). μf is the fluid viscosity,a function of temperature and pressure. ρ is the mass density of the mixture,defined by
Though the terms of the convection and relative acceleration of the fluids are insignificant in practice,they may lead to computational problems. Therefore,they are neglected here. The final simplified form of the linear momentum balance equations of the fluids and mixture read
where pf ,j represents the gradient of pf,and sf ij if the permeability coefficient of the pore fluid (liquid or gas) evaluated by
kij 0 is the intrinsic permeability tensor of the medium,which is a constant for the same medium. krf (nf ) is the relative permeability of the fluids,which is a function of saturation in general. The hysteresis effect in the permeability is not apparent. Therefore,it is not considered in this study. The relative permeability is assumed to be related to the suction according to the Mualem expression[40]:
where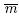
is a material parameter,which can be obtained by a test. Se is the effective degree of
saturation expressed by
For an isothermal problem,the energy balance is exactly satisfied. 5 Finite-element formulation
The four-node quadrilateral isoparametric elements are typically used in this finite-element
formulation with linear interpolation for both displacement and pressure fields. Employ the
Galerkin method. Then,the above coupled governing equations,namely,Eqs. (38),(39),and
(41),can be discretized spatially. The displacement and pore pressures are discretized as
u =
and pf = ,where N and Nf are the displacement matrix and the pore pressure
shape function matrix. The semi-discrete calculation format of the finite-element method can
be now presented as follows:
(I) The natural boundary conditions do not express explicitly but hide in the boundary conditions of the governing equations:
(II) The basic boundary conditions can give the unknowns directly,and they are as follows:
The nodal displacements and pressures corresponding to these conditions will be ruled out from the global primary unknown vector,and the conditions satisfy
At the initial state t = 0,the concerned field must be determined before the transient process is analyzed,i.e.,
The initial pressures and effective stresses can be evaluated by a static analysis. 5.2 Time integration algorithm
The time integration of the spatially discrete governing equations is an important part in the numerical analysis. In this research,the Hilber-Hughes-Taylor α-Method[41] together with a predictor corrector algorithm is used to integrate the finite-element formulation in the time domain,where the time step can be subdivided automatically into substeps to keep the local error close to a specified tolerance. In addition,when applying subincrementation,the same rate is applied to all strain components including the suction. This method improved Newmark’s method by incorporating an additional parameter α,which has second-order accuracy and unconditional stability in linear problems when the parameters α,β,and γ satisfy the conditions
Provide the solution at tn. Then,the next step is to find the solution at tn+1 (Δt = tn+1 −tn). The residual formula of Eq. (47) can be discretized as follows:
Introduce Newmark’s Scheme It is worth pointing out that the coefficient matrixes are solution-dependent and they must be updated in every time step. The solution of the non-linear system is actually achievable by the Newton-Raphson iteration with a suitable Jacobian matrix and convergence rule. For the ith iteration,linearizing the residual equation gives where Xi is the tangent modulus defined by
and KT is the stiffness matrix defined by
in which B is the strain-displacement matrix. The consistent tangential modulus Dn+1 shown in Eq. (33) of each element is assembled in the total stiffness matrix KT . KT is consistent with the return-mapping Scheme. It is shown that this approach will preserve the quadratic rate of the asymptotic convergence of the iterative Scheme. The incremental acceleration is calculated by
The iteration procedure is summarized as follows: calculate the incremental acceleration Δ¨ui+1 by solving Eq. (52),calculate ü,u,and u by Eqs. (52),(49),and (50),respectively,and update the matrices according to the new values. Go to next time step after the convergence criteria are satisfied. The time-stepping Scheme adopting a predictor/multi-corrector algorithm is shown as follows:
(i) Let i = 0.
(ii) Calculate
(iii) Compute e(ü n+1i),Xi,and Δ¨ui+1 = −(Xi)-1 · e(ü n+1i).
(iv) Compute(n+1i+1)
(iv) If
then go to the next time step; else,let i := i + 1,and go to Step (iii).
The formulation presented above can be degenerated to the quasi-static format expressed by Cu +Kpu + Pint = Fext.
Combined with the integration of the constitutive model,a complete finite-element formulation for the coupled transient hydro-mechanical problems in unsaturated soils is presented. The displacements and pore pressures are considered as the primary nodal unknowns in the global differential equations. The finite-element formulation and the new constitutive model integration are implemented into the finite-element code,i.e.,U-DYSAC2,whose effectiveness and robustness has been verified by Wei[28]. With appropriate initial and boundary conditions, the values of the state variables at various points and time in the soil medium can be obtained by the simultaneous solution of these equations. 6 Numerical example 6.1 One-dimensional (1D) gravity-driven seepage problem
To validate the model,we first perform an experiment the same as Liakopoulos[42] on a column of the Del Monte sand (see Fig. 5). Before the start of the experiment,water is continuously injected from the top and allows free drainage at the bottom through a porous stone, until the uniform flow conditions are achieved. At the start of the experiment,the water supply on the top ceases. The suction at several points along the sand column are measured during the drainage due to the gravitational effect. During the experiment,the air can flow freely through the top boundary.
 |
| Fig. 5 Liakopoulos test problem |
The Del Monte sand has a porosity of 0.3,and its hydraulic properties are measured in an independent set of experiments. The material parameters are as follows:
where ρs is the solid grain density,ρl is the water density,ρg is the air density,Kl is the bulk
modulus of water,k0 is the intrinsic permeability,μl is the water viscosity,μg is the air viscosity,
and 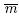is the parameter for permeability.
The relationship between the suction and the degree of the saturation is shown in Fig. 6, which presents the apparent capillary hysteresis phenomenon.
 |
| Fig. 6 Cyclic soil-water character curve of sand (SWCC) |
The mechanical parameters of the Del Monte sand are not available. Therefore,they are assumed to be the typical values for sand,which are as follows:
For the numerical calculations,the sand column experiment can be viewed as a 1D problem, which is divided into 10 four-node isoparametric finite elements of equal size. The boundary conditions are as follows:
(i) For the bottom surface,ux = 0.0,uy = 0.0,and pl = pg = 0.0.
(ii) For the lateral surface,ux = 0.0,ql = 0.0,and qg = 0.0.
(iii) For the top surface,ql = 0.0,and pg = 0.0.
In the above equations,pl and pg represent the parts of the fluid pressures in excess of the atmospheric pressure.
The sand column is initially fully water saturated and hydrostatic conditions applied for t = 0.0. All the displacements are related to these initial displacements which correspond to the equilibrium state.
The numerical results are presented in Fig. 7. In the experiment of Liakopoulos[42],the pore water pressures were measured at 5 minutes,10 minutes,20 minutes,30 minutes,60 minutes, and 150 minutes,respectively. However,the pore air pressures,the degree of saturations,and the displacements were not available. Figure 7(a) shows the distributions of the pore water pressures within the column at different time,while Fig. 7(b) shows the changes of the pore water pressures with time at three different heights. After the water supply ceases,i.e.,when t = 0.0,the pore pressures decrease rapidly,and then tend to the stable state during the desaturation due to the gravitational effect. The simulation and experimental results show the same tendency. From Figs. 7(a) and 7(b),we can see that the agreement between the numerical simulation and measured results is very good for the time after 30 minutes. However,in the first 30 minutes,the predicted pore water pressures decrease faster than the measured results. At the early stage of the experiment,the pore water pressures are very sensitive to the air entry value of the Del Monte sand. It is assumed to be 4 kPa in the numerical simulation. Figure 7(c) illustrates the distributions of the pore air pressures simulated along the sand column at different time. The air pressures are not available in the test. The numerical results agree well with the results obtained by Sheng et al.[43]. At a certain depth,the pore air pressure decreases to a minimal value first,and then increases again. From the above results,we can conclude that the pore air pressure has a significant effect on the two-phase flow solutions so that the assumption of the pore air pressure value equals the atmospheric pressure (one-phase flow approach) in unsaturated soils may lead to inadequate results. Figure 7(d) shows the variation of saturation across the soil column at different time. During the drainage process,the upper part (from 0.4m-1.0m) of the sand column becomes unsaturated. During the dewatering, the compaction of the sand takes place and the bulk stiffness increases,due to the increase in the suction. The evolution of the vertical displacement along the sand column is reported in Fig. 7(e). The suction is higher at the top of the soil column,resulting that the plastic deformation occurs during the drying process,which causes larger vertical displacements than other parts of the column. The comparison of the simulated and the measured results indicates a very good match,which verifies that the model can simulate the drying which will cause plastic deformation.
 |
| Fig. 7 Numerical results for 1D gravity-driven seepage |
However,in most natural processes,more cycles of drying and wetting take place due to seasonal variations. An experiment has been performed by Hoa et al.[44] on a soil column to study the influence of the capillary hysteresis effect on transient flows in saturated-unsaturated soils. The column is the same as in Fig. 5.
In the 1D experiment,a succession of constant flux cycles of drying and wetting is applied at the bottom boundary of the vertical sand column (see Fig. 8). The chosen constant flux is so small that the influence of air can be neglected. The pore water pressures and water contents at different time along the column are measured in this experiment. In this case,the pore air pressures are assumed to be equal to the atmospheric pressure.
The utilized material is the Fontainebleau sand with the porosity of 0.34,the intrinsic permeability k0 of 7.37×10-12m2,and the solid grain density ρs of 2.65×103 kg·m−3. Other parameters the same as those in Subsection 6.1. The parameters for the coupling model are summarized as follows:
For the numerical calculations,the column of soils is divided into 100 elements of equal size. The boundary conditions are as follows: (i) For the bottom surface,
(ii) For the lateral surface,
(iii) For the top surface,
At the start of the experiment,i.e.,t = 0.0,the column is saturated in the initial condition. The variation of the flux imposed on the bottom boundary is shown in Fig. 8. The water is withdrawn in a specific flux at the end of the column,then the soil becomes unsaturated. After a period of time,the direction is reversed and the water is injected into the column with the same rate. At the last stage,the drying process is repeated. With the changes of the flux direction at the bottom boundary,the soil experiences cyclic drying and wetting. In this case, the discanning curves of higher orders need to be considered.
 |
| Fig. 8 Flux boundary condition at lower end of column |
The numerical results are presented in Fig. 9. Figures 9(a) and 9(b) show the evolutions of the saturations and the pore water pressures with time at the heights of 60 cm and 80 cm, respectively. The figures show that both the saturation and the pore water pressure decrease during the pumping. When water is injected into the column,the soil turns into the wetting process. The pore water pressure and the saturation are increasing. The saturation and the pore water pressure at the height of 80 cm are apparently less than the values at the height of 60 cm,and the magnitude of the change during the wetting process is also smaller.
Figure 9(c) shows the evolution of the vertical displacement at the top boundary,where the experimental data are not available. The simulation results show that the soil is compacted during the drying process and hardened with the increase in the suction. Afterwards,the soil becomes rebounding in the wetting process due to the decrease in the suction. The material remains in the elastic domain during the whole wetting process,and no collapse compression occurs. A further discussion on the results shown in Figs. 9(b) and 9(c) allows pointing out that the pore pressure evolution is indeed in agreement with the solid skeleton deformation.
The agreement between the simulated and measured results reveals that the new numerical model is capable of predicting the behaviors of unsaturated soils during cyclic drying-wetting processes. The current hydraulic state not only is related to the current values of the suction and saturation,but also depends on the experienced hydraulic history. The new model can describe the effect of the arbitrary variation of the hydraulic path.
 |
| Fig. 9 Numerical results of 1D soil column flow problem |
A typical 2D problem is analyzed to investigate the performance of the finite-element formulation developed in this study. In this example,we consider the problem of a strip footing resting on an elastoplastic soil layer. The foot is subjected to a set of uniform load of 100kPa. The finite element mesh (150 elements) and boundary conditions used to analyze the problem are shown in Fig. 10. Due to the symmetry of the foundation,only one half is considered. The problem is analyzed as a plain strain one.
 |
| Fig. 10 Finite element mesh and boundary condition for 2D problem |
For the numerical calculations,the soil layer is divided into 150 elements of equal size. The boundary conditions are as follows:
(i) For the bottom surface,ux = 0.0,uy = 0.0,and ql = qg = 0.0.
(ii) For the top surface,σx = 0.0,σy = 100 kPa,and pg = 0.0.
(iii) For the lateral surface,ux = 0.0,ql = 0.0,and pg = 0.0.
In all analyses,the initial stresses in the soil layer are generated by gravity. During this stage,the material is assumed to be nonlinearly elastic with the initial degree of saturation 70%. The corresponding negative pore water pressure can then be obtained. With the initial hydrostatic stresses,the initial yield surface locations can be determined by considering the overconsolidation ratio 1.2. After the nodal displacement is initialized to zero,a uniform load is applied to the left five nodes on the top boundary. The parameters of the coupling constitutive model are as follows:
The typical tolerance values in practical analyses are used in the analysis,where the yield surface tolerance FTOL is set to 10−6. The residual force norm error tolerance RTOL is set to 10−3,which controls the accuracy of the time integration. It is worth noting that changing them by one or two orders of magnitudes does not affect the results significantly in general. The convergence rate of the global analysis can be seen from Table 1,which shows that the performance of this new numerical model is good.
Finally,the calculation results of the finite-element procedure are summarized in Fig. 11. The evolution of the displacement at the top boundary is given in Fig. 11(a). Clearly,the displacement near the loading boundary is significantly larger than that in other areas. In the beginning,the displacement develops rapidly due to the applied loading,increases further with time going on,and finally approaches a steady state. Figure 11(b) gives the distributions of the displacement within the soil layer along the left section A-B at different time. Figure 11(c) presents the distributions of the pore water pressure along the section AB at 0.1,0.2,0.3,1.5, and 4.4 h. It clearly shows that the pore water transports with time and finally is accumulated under the foundation due to the impervious boundary. Figures 11(d) and 11(e) illustrate the distributions of the pore air pressures and saturations along the line A-B. The pore pressures and saturations along the line A-B have the corresponding increase,which can be seen from Figs. 11(c)-11(e) clearly. The initial pore pressures and saturations are the same in the whole soil mass. When applying the load,the pore water and air pressures have sudden changes at the early stage,and then attain the equilibrium state slowly with the development of time. The corresponding saturations have the similar trend (see Fig. 11(e)). The water saturations near the top surface are lower than those inside the soil layer since the top surface is the only drained boundary. Finally,the pressures and saturations in the soil layer reach the constant values,respectively,under the constant loading on the top boundary.
 |
| Fig. 11 Numerical results of finite-element procedure |
The water pressure in the shallower area dissipates faster than the deeper zone. The pore water pressures in the deeper area increase slightly in the beginning due to the increase in the air pressure under loading. As a consequence,the pore pressures arrive at the stable state and distribute on an oblique line approximately,which cause that the degree of saturation at the upper part is smaller than that at the lower part. Remarkably,the model simulations are consistent with previous results[43].
Figure 12 shows the evolution of the plastic volume deformation of the elements 99,108, 136,and 137. The elements nearer to the loading nodes experience larger plastic deformation.
From the above analysis,it appears that the constitutive model provides a relatively simple and efficient way of the coupling hydraulic and mechanical behavior of unsaturated soils in the finite-element analysis. Overall,it can be concluded that the new model is capable describing the coupled hydro-mechanical behavior of unsaturated soils. Extensions like mass exchanges between the constituents or heat transfer can easily be included in the model.
 |
| Fig. 12 Evolution of plastic volume deformation of different elements |
This article presents the implementation of the new constitutive model of the coupling capillary hysteresis and skeleton deformation into a fully coupled transient hydro-mechanical finite-element model. The stress integration Scheme is based on the implicit return-mapping method,where the suction is treated as an additional strain component. With the constitutive relationships,the complete finite-element formulation for unsaturated soils is presented,which can be used to analyze and solve the coupling hydro-mechanical problems of unsaturated soils. Numerical examples are presented to demonstrate the global accuracy and stability of these techniques. Appendix A
where 
i(t) and 
nf
are the prescribed values of the load vector and the fluid rate on the boundaries.
NAs
and NBf are the space shape functions of the solid framework and the porous fluid, respectively.
They all may be the same or not. Subscripts A and B are the node numbers of the finite elements.
| [1] | Fredlund, D. G. and Rahardjo, H. Soil Mechanics for Unsaturated Soils, John Wiley & Sons Inc., New York (1993) |
| [2] | Poulovassilis, A. Hysteresis of pore water: an application of the concept of independent domains. Soil Science, 93, 405-412 (1962) |
| [3] | Topp, G. C. and Miller, E. E. Hysteresis moisture characteristics and hydraulic conductivities for glass bead media. Soil Science Society of America Journal, 30, 156-162 (1966) |
| [4] | Cadoret, T., Mavko, G., and Zinszner, B. Fluid distribution effect on sonic attenuation in partially saturated limestones. Geophysics, 63, 154-160 (1998) |
| [5] | Wei, C. F. and Dewoolkar, M. M. Formulation of capillary hysteresis with internal state variables. Water Resources Research, 42, W07405 (2006) |
| [6] | Muraleetharan, K. K., Liu, C. Y., Wei, C. F., Kibbey, T. C. G., and Chen, L. X. An elastoplatic framework for coupling hydraulic and mechanical behavior of unsaturated soils. International Journal of Plasticity, 25, 473-490 (2008) |
| [7] | Li, X. S. Thermodynamics-based constitutive framework for unsaturated soils 1: theory. Géotechnique, 57, 411-422 (2007) |
| [8] | Ma, T. T., Wei, C. F., Chen, P., Tian, H. H., and Sun, D. A. A unified elastoplastic constitutive model of unsaturated soils with considering the effect of capillary hysteresis. Journal of Applied Mathematics, 2013, 537185 (2013) |
| [9] | Alonso, E. E., Gens, A., and Josa, A. A constitutive model for partially saturated soils. Géotechnique, 40, 405-430 (1990) |
| [10] | Bolzon, G., Schrefler, B. A., and Zienkiewicz, O. C. Elastoplastic soil constitutive laws generalized to partially saturated states. Géotechnique, 46, 279-289 (1996) |
| [11] | Wheeler, S. J., Sharma, R. S., and Buisson, M. S. R. Coupling of hydraulic hysteresis and stressstrain behaviour in unsaturated soils. Géotechnique, 53, 41-54 (2003) |
| [12] | Sun, D. A., Sheng, D., and Sloan, S. W. Elastoplastic modelling of hydraulic and stress-strain behaviour of unsaturated soils. Mechanics of Materials, 39, 212-221 (2007) |
| [13] | Vaunat, J., Cante, J. C., Ledesma, A., and Gens, A. A stress point algorithm for an elastoplastic model in unsaturated soils. International Journal of Plasticity, 16, 121-141 (2000) |
| [14] | Runesson, K. Implicit integration of elastoplastic relations with reference to soils. International Journal for Numerical and Analytical Methods in Geomechanics, 11, 315-321 (1987) |
| [15] | Macari, E. J., Hoyos, L. R., and Arduino, P. Constitutive modeling of unsaturated soil behavior under axisymmetric stress states using a stress/suction-controlled cubical test cell. International Journal of Plasticity, 19, 1481-1515 (2003) |
| [16] | Zhang, H.W., Heeres, O. M., de Borst, R., and Schrefler, B. A. Implicit integration of a generalized plasticity constitutive model for partially saturated soil. Engineering Computations, 18, 314-336 (2001) |
| [17] | Simo, J. C. and Taylor, R. L. A return mapping algorithm for plane stress elastoplasticity. International Journal for Numerical Methods in Engineering, 22, 649-670 (1986) |
| [18] | Sheng, D. C., Sloan, S. W., Gens, A., and Smith, D. W. Finite element formulation and algorithms for unsaturated soils, part I: theory. International Journal for Numerical and Analytical Methods in Geomechanics, 27, 745-765 (2003) |
| [19] | Zienkiewicz, O. C., Chan, A. H. C., Pastor, M., Paul, D. K., and Shiomi, T. Static and dynamic behaviour of soils: a rational approach to quantitative solutions, I: fully saturated problems. Proceedings of the Royal Society of London. Series A, Mathematical and Physical Sciences, 429, 285-309 (1990) |
| [20] | Zienkiewicz, O. C., Xie, Y. M., Schrefler, B. A., Ledesma, A., and Bicanic, N. Static and dynamic behaviour of soils: a rational approach to quantitative solutions, II: semi-saturated problems. Proceedings of the Royal Society of London, Series A, Mathematical and Physical Sciences, 429, 311-321 (1990) |
| [21] | Laloui, L., Klubertanz, G., and Vulliet, L. Solid-liquid-air coupling in multiphase porous media. International Journal for Numerical and Analytical Methods in Geomechanics, 27, 183-206 (2003) |
| [22] | Li, X. K., Zienkiewicz, O. C., and Xie, Y.M. A numerical model for immiscible two-phase fluid flow in a porous medium and its time domain solution. International Journal for Numerical Methods in Engineering, 30, 1195-1212 (1990) |
| [23] | Schrefler, B. A. and Zhan, X. A fully coupled model for water flow and airflow in deformable porous media. Water Resources Research, 29, 155-167 (1993) |
| [24] | Olivella, S., Carrera, J., Gens, A., and Alonso, E. Nonisothermal multiphase flow of brine and gas through saline media. Transport in Porous Media, 15, 271-293 (1994) |
| [25] | Thomas, H. R. and He, Y. A coupled heat-moisture transfer theory for deformable unsaturated soil and its algorithmic implementation. International Journal for Numerical Methods in Engineering, 40, 3421-3441 (1997) |
| [26] | Nowamooz, H., Mrad, M., Abdallah, A., and Masrouri, F. Experimental and numerical studies of the hydromechanical behaviour of a natural unsaturated swelling soil. Canadian Geotechnical Journal, 46, 393-410 (2009) |
| [27] | Simoni, L., Salomoni, V., and Schrefler, B. A. Elastoplastic subsidence models with and without capillary effects. Computer Methods in Applied Mechanics and Engineering, 171, 491-502 (1999) |
| [28] | Wei, C. F. Static and Dynamic Behavior of Multiphase Porous Media: Governing Equations and Finite Element Implementation, Ph.D. dissertation, University of Oklahoma, Oklahoma (2001) |
| [29] | Houlsby, G. T. The work input to an unsaturated granular material. Géotechnique, 47, 193-196 (1997) |
| [30] | Roscoe, K. H. and Burland, J. B. On the generalized stress-strain behavior of 鈥渨et鈥?clay. Engineering Plasticity, 535-609 (1968) |
| [31] | Tamagnini, R. An extended Cam-clay model for unsaturated soils with hydraulic hysteresis. Géotechnique, 54, 223-228 (2004) |
| [32] | Feng, M. and Fredlund, D. G. Hysteresis influence associated with thermal conductivity sensor measurements. Proceeding from Theory to the Practice of Unsaturated Soil Mechanics, Regina, 651-657 (1999) |
| [33] | Borja, R. I. and Lee, S. R. Cam-clay plasticity, part 1: implicit integration of elasto-plastic constitutive relations. Computer Methods in Applied Mechanics and Engineering, 78, 49-72 (1990) |
| [34] | Simo, J. C. and Taylor, R. L. Consistent tangent operators for rate-independent elastoplasticity. Computer Methods in Applied Mechanics and Engineering, 48, 101-118 (1985) |
| [35] | Aravas, N. On the numerical integration of a class of pressure-dependent plasticity models. International Journal for Numerical Methods in Engineering, 24, 1395-1416 (1987) |
| [36] | Wei, C. F. and Muraleetharan, K. K. A continuum theory of porous media saturated by multiple immiscible fluids: 1, linear poroelasticity. International Journal of Engineering Science, 40, 1807- 1833 (2002) |
| [37] | Wei, C. F. and Muraleetharan, K. K. A continuum theory of porous media saturated by multiple immiscible fluids: 2, Lagrangian description and variational structure. International Journal of Engineering Science, 40, 1835-1854 (2002) |
| [38] | Hassanizadeh, S. M. and Gray, W. G. General conservation equations for multi-phase systems: 1, averaging procedure. Advances in Water Resources, 2, 131-144 (1979) |
| [39] | Hassanizadeh, S. M. and Gray, W. G. General conservation equations for multi-phase systems: 2, mass, momenta, energy, and entropy equations. Advances in Water Resources, 2, 191-203 (1979) |
| [40] | Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resources Research, 12, 513-522 (1976) |
| [41] | Hilber, H. M., Hughes, T. J. R., and Taylor, R. L. Improved numerical dissipation for time integration algorithms in structural dynamics. Earthquake Engineering and Structural Dynamics, 5, 283-292 (1977) |
| [42] | Liakopoulos, A. C. Transient Flow Through Unsaturated Porous Media, Ph.D. thesis, University of California, Berkeley (1965) |
| [43] | Sheng, D. C., Smith, D. W., Sloan, S. W., and Gens, A. Finite element formulation and algorithms for unsaturated soils, part II: verification and application. International Journal for Numerical and Analytical Methods in Geomechanics, 27, 767-790 (2003) |
| [44] | Hoa, N. T., Gaudu, R., and Thirriot, C. Influence of the hysteresis effect on transient flows in saturated-unsaturated porous media. Water Resources Research, 13, 992-996 (1977) |