Shanghai University
Article Information
- Jian-kang LIU, Zhou-shun ZHENG. 2014.
- Efficient high-order immersed interface methods for heat equations with interfaces
- Appl. Math. Mech. -Engl. Ed., 35(9): 1189-1202
- http://dx.doi.org/10.1007/s10483-014-1851-6
Article History
- Received 2013-4-25;
- in final form 2014-1-15
2 School of Mathematics and Statistics, Central South University, Changsha 410083, P. R. China;
3 State Key Laboratory of Porous Metal Materials, xi'an 710016, P. R. China
We consider the following two-dimensional (2D) parabolic interface problem:
The initial condition is The boundary condition is The jump condition is In the above equations,the domain Ω is divided by a curve Γ into two parts,i.e.,Ω+ and Ω-. The source term f and the initial value u0 are piecewise smooth across Γ,where s is the arc-length parameterization of Γ,and n is the unit outward normal vector of Γ,pointing to the Ω+ side (see Fig. 1). The jump,[·],is defined as the difference of the limiting values from two sides of the interface,and can be written as
Since the interface is immersed in the domain Ω,we also call the jump condition (4) the inner boundary condition and the boundary condition (3) the outer boundary condition. With the poor initial value u0(x,y) and the source term f(x,y,t),the solution is non-smooth across the interface.
 |
| Fig. 1 Diagram of interface and outward normal vector |
In recent years,many contributions have been made to solve interface problems. In 1972,an immersed boundary method (IBM) was proposed by Peskin for interface problems[1]. A uniform Cartesian grid was used to describe the velocity of the fluid. The immersed elastic structure was described by Lagrangian points. The interaction between the elastic structure and the fluid was determined by smoothed δ functions. Since it is convenient in handling complex boundaries, it has been successively used to simulate the vibrations of cochlear basilar membrane[2],blood flow in human heart[3],aquatic locomotion[4],platelet aggregation during clotting[5],flow with suspension particles[6] and so on. Nevertheless,since δ functions are treated approximately smooth,the convergence rate is first-order in the maximum norm.
An efficient numerical method[7,8],the immersed interface method (IIM),was proposed by Leveque and Li for elliptic interface problems. It has a second-order accuracy in the maximum norm. The finite difference scheme of the IIM is the same as the standard difference scheme away from the interface. When the interface passes through the difference stencil,the difference scheme would be modified by incorporating the jump condition of the primary variables across the interface. However,for two-dimensional problems,the IIM adds the sixth point to the standard five-point stencil,which produces a non-symmetric coefficient matrix. Li and Ito[9] improved the IIM and proposed the maximum principle preserving IIM (MPPIIM)[9]. TheMPPIIM can produce a diagonally dominant coefficient matrix,and it has been implemented with the multigrid method[10]. Wiegmann and Bube[11] proposed the explicit jump IIM (EJIIM) for elliptic interface problems. Berthelsen[12] proposed the decomposed IIM for variable coefficient elliptic interface problems. Li[13] proposed the fast iterative IIM (FIIIM) for elliptic interface problems with discontinuous coefficients. Bedrossian et al.[14] proposed the second-order virtual node method for elliptic interface problems. Zhou et al.[15] and Pan et al.[16] proposed the matched interface and boundary method for elliptic problems with interfaces. Chen and Strain[17] proposed a new Krylov-accelerated multigrid method with piecewise-polynomial discretization for elliptic interface problems. Joshi and Kumar[18] used the decomposed IIM to simulate the temperature distribution in multilayer thin films. Huang and Li[19] and Beale and Layton[20] showed that the local truncation error could be one-order lower along the interface without influencing the whole accuracy.
For time-dependent problems,we often adopt the implicit method,which can eliminate the restriction of the time step. However,at each time step,a large linear system of equations needs to be solved in two- or three-dimensional problems. One can use the fractional step method to avoid this problem. Peaceman and Rachford’s alternative direction implicit (PRADI) scheme[21] is one of the fractional step methods,which has the second-order convergence and is unconditionally stable for two-dimensional problems. In Refs. [22] and [23],the PR-ADI scheme was used to solve heat interface problems and Stefan problems,respectively. Kandilarov and Vulkov[24] proposed the immersed interface based θ-difference schemes for two-dimensional heat diffusion equations with singular own source. Li et al.[25] proposed the prediction-correction implicit method for thermo-elastic equations with discontinuities. Li and Ito[26] constructed a fourth-order accuracy M-matrix finite difference method for interface problems,which produced a large sparse linear system in several-dimensions.
To the best of our knowledge,no contribution has been made to construct high order compact-alternative direction implicit (HOC-ADI) finite difference scheme for parabolic interface problems. This paper intends to construct HOC-ADI IIM schemes for heat conduction problems with interfaces. The proposed method achieves the second-order convergence in time and the fourth-order convergence in space in the maximum norm. The Richardson extrapolation method is used to improve the accuracy to fourth-order in time. The interface is represented by the level set function[27] due to its strength and simplicity in describing complex shapes.
The remainder of the paper is organized as follows. Section 2 gives some preparations for this paper. In Section 3,the HOC-ADI IIM scheme for 2D parabolic interface problems is constructed,and the computation of required jump conditions is also given. Two numerical experiments are shown in Section 4 before conclusions are summarized in Section 5. 2 Preliminaries 2.1 Discretization
Assume that the domain Ω is a rectangle [a,b] × [c,d] and the interface Γ is a circle. The domain Ω is discretized by a uniform M × N grid

where Δx and Δy are space steps in the x- and y-axis directions defined by

The interface is not always aligned with the mesh grids. A mesh point (xi,yj) is regular if all points in the difference stencil are on the same side of the interface. On the contrary,if at least one point is on the other side of the interface,it is irregular. In Fig. 2,the mesh grids of 25×25 subdivisions with reference to a five-point stencil are displayed. Assume that un i,j represents the value of u(xi,yj,tn),where tn is the nth time level,and Un i,j is the numerical approximation of u(xi,yj,tn).
 |
| Fig. 2 Mesh grids of 25 × 25 subdivisions |
Since the shape of the interface may be fairly complex,a smooth auxiliary function,i.e., the level set function,φ(x,y) is introduced,which is defined as φ(x,y) = ±ds,where ds is the shortest distance from (x,y) to the interface Γ. Thus,the set of points with φ(x,y) = 0 represents the interface,i.e.,
The set of points with φ(x,y) < 0 and the set of points with φ(x,y) > 0 represent the two disjoint domains Ω- and Ω+,respectively (see Fig. 1). The outward normal vector n can be approximated by n = ∇φ/|∇φ| at any point. For example,if the interface Γ is a circle centered at zero with the radius r,then the level set function φ(x,y) can be set as φ(x,y) =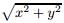 If (X,Y ) locates at the circle,then
φ(X,Y) = 0. If (X,Y ) lies inside the circle,then φ(X,Y ) < 0. If (X,Y ) lies outside the
circle,then φ(X,Y ) > 0. For a grid point (xi,yj ),if (xi,yj ),(xi+1,yj),(xi-1,yj),(xi,yj+1),
and (xi,yj-1) are at the same side of the interface,then we say that (xi,yj) is a regular point.
Otherwise,if one of these four points lies at the other side of the interface,(xi,yj) is an irregular
point.
With the help of the level set function φ(x,y),the locations of the intersection between the
interface and the grid lines can be determined conveniently. Suppose that the interface lies
between (xi,yj) and (xi+1,yj ). If we define
If (X,Y ) locates at the circle,then
φ(X,Y) = 0. If (X,Y ) lies inside the circle,then φ(X,Y ) < 0. If (X,Y ) lies outside the
circle,then φ(X,Y ) > 0. For a grid point (xi,yj ),if (xi,yj ),(xi+1,yj),(xi-1,yj),(xi,yj+1),
and (xi,yj-1) are at the same side of the interface,then we say that (xi,yj) is a regular point.
Otherwise,if one of these four points lies at the other side of the interface,(xi,yj) is an irregular
point.
With the help of the level set function φ(x,y),the locations of the intersection between the
interface and the grid lines can be determined conveniently. Suppose that the interface lies
between (xi,yj) and (xi+1,yj ). If we define

then 0 ≤ θx ≤ 1,and the interface is located at
Similarly,when the interface lies between (xi,yj) and (xi,yj+1),if we define
then 0 ≤ θy ≤ 1,and the interface is located at
2.3 Corrected Taylor expansionsSince the primary variables are discontinuous or non-smooth across the interface,the traditional Taylor expansions are not valid. We need the following corrected Taylor expansions for interface problems.
Lemma 1 (corrected Taylor expansions) Suppose that the interface α lies between two arbitrary located grid points xi and xi+1 i.e.,xi < α < xi+1. Let Δx = xi+1 - xi and u ∈ Cl+1((xi,xi+1)\(α)). Then,we have the following corrected Taylor expansion of u(xi+1) about xi:
where the correction term C is defined as
The proof of Lemma 1 can be done analogously to Ref. [11] or Ref. [28]. 3 Numericalmethods 3.1 Rationale of HOC-ADI IIM
For convenience,we define four difference operators as follows:
where δ2x and δ2 y are the second-order central difference operators in the x- and y-directions, respectively,and I is the identity operator.It is well-known that the differential equation -d2u/ dx2 = f can be discretized by the three-point compact difference scheme expressed as Axui = Lxfi + O(Δx4),i.e.,L-1 x Axui = fi + O(Δx4), which has the fourth-order accuracy. Similar to that in Ref. [29],for Eq. (1),we have
where O(Δ4) denotes the O(Δx4) + O(Δy4) term. Applying the operator LxLy to both sides of Eq. (10),we obtain Employing the Crank-Nicolson time discretization,we have This discretization is obviously second-order in time and fourth-order in space,due to the use of the Crank-Nicolson type integrator in time with a fourth-order spatial discretization. Here and from now on,the subscript of space is suppressed.After rearranging and dropping the truncation error terms,we have
By adding the terms Δt2AyAxUn+1/4 and Δt2AxAyUn/4 to the left- and right-hand sides of Eq. (13),respectively,we get which has the same order of accuracy as Eq. (1). By introducing the intermediate variable U*, we can achieve the following two steps of the HOC-ADI difference scheme for Eq. (1): which are unconditionally stable,and can approximate Eq. (1) second-order in time and fourthorder in space for smooth problems.However,for interface problems,correction terms must be added to the right-hand side of Eq. (15) at irregular points. For the sake of the explicit computation of the correction term,we only add one correction term to the right-hand side of Eq. (15a). Then,the difference schemes become
This is the two steps of the HOC-ADI IIM difference scheme for interface problems,i.e., Eqs. (1)-(4). The boundary condition of the intermediate variable U* can be obtained by Eq. (16b). The computation of the correction term C in Eq. (16a) will be discussed in the following subsection. 3.2 Determination of correction term
In order to determine the correction term C in Eq. (16a),we should derive the equivalent difference scheme of Eq. (16). Substituting (Lx + ΔtAx/ 2 ) to Eq. (16b) and plugging it into Eq. (16a),we can obtain the equivalent difference scheme of Eq. (16) as follows:
Expanding the multiplication of operators in Eq. (17) by virtue of Eq. (9),we obtain where The following Theorem 1 gives the correction term C in Eq. (18).Theorem 1 (HOC-ADI IIM) For two-dimensional heat interface problems,Eqs. (1)-(4),if u ∈ C5(Ω\Γ) and f ∈ C3(Ω\Γ),then the difference scheme,Eq. (16),is second-order convergent in time and fourth-order convergent in space in the maximum norm. The correct term C is determined by
where
and

in which

where (x*,y*) is the intersection of the interface and the grid line. The sign “±” depends on the relative position between (x*,y*) and (xi,yj). Proof Substituting the exact solution u for the numerical solution U in Eq. (18),we have
where τ is the local truncation error at (xi,yj ). If (xi,yj) is a regular point,the correction term C is zero and the local truncation error τ is O(Δt2+Δ4). If (xi,yj) is an irregular point, we should determine the correction term C so that the local truncation error τ is O(Δt2 +Δ3) according to the existing convergence analyses[19,20].Since the interface is fixed,all quantities are continuous with time. Then,we can check the local truncation error of Eq. (21) by examining each part. The left-hand side of Eq. (21) gives
With respect to the operator -1/ 2AxLy on the right-hand side of Eq. (21),we have
where

For the term -1/ 2AxLy(un+1 + un),we achieve
where the correction terms Cx4,Cy4,and Cy4x0 can be obtained by Lemma 1 and satisfy the following equations:
Similarly,for the term -1/ 2LxAy(un+1 + un),we have
where following equations:
For the term - 1M(un+1 - un)/ Δt,we obtain
where
For the term -ΔtAxAy(un+1 - un)/ 4 ,we get
where
Finally,for the term Mfn+1/2 ,since the source term f is discontinuous across the interface,and it is a known function,we just need to cancel it by C.
Then,the proof of the theorem ends by plugging Eqs. (22)-(26) into Eq. (21) after some manipulations. 3.3 Extrapolation in time direction
From Eq. (12),we can see that the above difference scheme of Eq. (16) is fourth-order in space and second-order in time. Suppose that the numerical solution U is the function of Δt, Δx,and Δy. Then,we have
where the constant α is independent of Δt. If we fix the space steps Δt,Δx,and Δy and halve the time step,then we get Combining Eqs. (27) and (28),after some manipulations,we obtain That is to say,the left-hand side of Eq. (29) approximates the solution u with the fourth-order accuracy in both temporal and spatial directions. This is the Richardson extrapolation in the time direction. It makes the final solution to be fourth-order accurate in both the temporal and spatial dimensions. Although the extrapolation requires three times as much computation as the original algorithm,the resulting high-order accuracy allows the use of much larger time steps in the computation.If we want to acquire a totally fourth-order accuracy in both time and space without the Richardson extrapolation in the time direction,the time step needs to be the square of the space step. However,when the Richardson extrapolation is used to improve the accuracy of the time,the time step can just be taken the same as that in space. It will be seen in Section 4 that the Richardson extrapolation can significantly improve the efficiency and the accuracy of the method. 3.4 Computation of jump condition
Since the jump conditions on the interface are usually defined in the normal or tangential direction,a local coordinate system is adopted to derive more jump conditions on the interface. At (x*,y*) on the interface,let
where θ is the angle between the x- and ζ-axes. The ζ-axis is normal to the interface while the η-axis is tangential (see Fig. 3). Under the local coordinate system,Eq. (1) is unchanged. In the neighborhood of the point (x*,y*),we parameterize Γ locally by ζ = x(η) and η = η. If the interface is smooth at (x*,y*),we have χ(0) = 0 and χ’(0) = 0,where x’’(0) is the curvature of the interface at (x*,y*). |
| Fig. 3 Local coordinate system |
By virtue of the jump conditions [u] and [un] in Eq. (4),similar to Refs. [22] and [26],we can obtain the following jump conditions:

Analogously,the jump conditions of the third derivatives read

and the jump conditions of the fourth derivative derivatives read

Thus,the jump conditions of u in the x- and y-directions can be given by

where c = cosθ and s = sinθ. 4 Numerical experiments
Several numerical experiments are conducted to check the accuracy of the proposed method. Here,we list two of them,in which,the interface Γ is defined by a circle x2 +y2 = 0.25 and the solution domain Ω = [-1,1] × [-1,1]. Two examples are conducted on a personal computer with Intel(R) Core(TM)2 Duo CPU and 1 024MB Memory. In order to illustrate the efficiency of the Richardson extrapolation method,the CPU time is shown in each example.
The convergence order is computed by

where the maximum norm is defined as

4.1 Example 1
This example is chosen from Ref. [22] to test the convergence order of the HOC-ADI IIM scheme in Eq. (16),which is a popular benchmark example for parabolic interface problems. The source term f(x,y,t) is defined as
where r =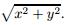 The initial and boundary conditions are specified so that the exact
solution is
In this example,both the function u and its normal derivative un have jumps. The required
jumps in u are chosen from Eq. (32). Table 1 shows the convergence analysis of this example.
The initial and boundary conditions are specified so that the exact
solution is
In this example,both the function u and its normal derivative un have jumps. The required
jumps in u are chosen from Eq. (32). Table 1 shows the convergence analysis of this example.
The source term f(x,y,t) in this example is defined as
where
The initial and boundary conditions are specified so that the exact solution is
The required jumps in u and un are determined by Eq. (34). The grid refinement analysis is given in Table 2.In this paper,we construct an HOC-ADI IIM scheme for two-dimensional heat equations with discontinuity along the interface. It can reduce the high dimensional heat interface problem into several one-dimensional problems. The space derivatives are discretized with the HOC difference scheme with proper correction terms at irregular points. The time direction is integrated by the Crank-Nicolson scheme combined with the Richardson extrapolation to improve the accuracy in time to fourth-order. The numerical examples in Section 4 show that if we want to get a totally fourth-order accuracy in both time and space,we can either take Δt = Δx2 without extrapolation or take Δt = Δx with extrapolation in the time direction. It can be found that both methods have the fourth-order convergence. However,the CPU time spent on the former is much longer than that on the latter. Hence,we can conclude that when the interface is fixed,the variables are continuous with time,and the Richardson extrapolation can significantly improve the accuracy and efficiency of the problem.
Acknowledgements The authors thank the supports from the Institute of Applied Software of Central South University and the High Performance Computing Platform of Central South University, China. The authors wish to thank the anonymous reviewers for their valuable comments and suggestions,which help to improve the paper.
| [1] | Peskin, C. S. Flow patterns around heart valves: a numerical method. Journal of Computational Physics, 10, 252-271 (1972) |
| [2] | Givelberg, E. Modeling elastic shells immersed in fluid. Communications on Pure and Applied Mathematics, 57, 283-309 (2004) |
| [3] | Peskin, C. S. and McQueen, D. M. A three-dimensional computational method for blood flow in the heart, I: immersed elastic fibers in a viscous incompressible fluid. Journal of Computational Physics, 81, 372-405 (1989) |
| [4] | Cortez, R., Fauci, L., Cowen, N., and Dillon, R. Simulation of swimming organisms: coupling internal mechanics with external fluid dynamics. Computing in Science & Engineering, 6, 38-45 (2005) |
| [5] | Wang, N. T. and Fogelson, A. L. Computational methods for continuum models of platelet aggregation. Journal of Computational Physics, 151, 649-675 (1999) |
| [6] | Uhlmann, M. An immersed boundary method with direct forcing for the simulation of particulate flows. Journal of Computational Physics, 209, 448-476 (2005) |
| [7] | Leveque, R. J. and Li, Z. The immersed interface method for elliptic equations with discontinuous coefficients and singular sources. Journal on Numerical Analysis, 31, 1019-1044 (1994) |
| [8] | Li, Z. A note on immersed interface method for three-dimensional elliptic equations. Computers & Mathematics with Applications, 31, 9-17 (1996) |
| [9] | Li, Z. and Ito, K. Maximum principle preserving schemes for interface problems. Journal of Scientific Computing, 23, 339-361 (2001) |
| [10] | Adams, L. and Li, Z. The immersed interface/multigrid methods for interface problems. Journal on Scientific Computing, 24, 463-479 (2003) |
| [11] | Wiegmann, A. and Bube, K. P. The explicit-jump immersed interface method: finite difference methods for PDEs with piecewise smooth solutions. Journal on Numerical Analysis, 37, 827-862 (2000) |
| [12] | Berthelsen, P. A. A decomposed immersed interface method for variable coefficient elliptic equations with non-smooth and discontinuous solutions. Journal of Computational Physics, 197, 364- 386 (2004) |
| [13] | Li, Z. A fast iterative algorithm for elliptic interface problems. Journal on Numerical Analysis, 35, 230-254 (1998) |
| [14] | Bedrossian, J., von Brecht, J. H., Zhu, S., Sifakis, E., and Teran, J. M. A second order virtual node method for elliptic problems with interfaces and irregular domains. Journal of Computational Physics, 229, 6405-6426 (2010) |
| [15] | Zhou, Y. C., Zhao, S., Feig, M., and Wei, G. W. High order matched interface and boundary method for elliptic equations with discontinuous coefficients and singular sources. Journal of Computational Physics, 213, 1-30 (2006) |
| [16] | Pan, K., Tan, Y., and Hu, H. An interpolation matched interface and boundary method for elliptic interface problems. Journal of Computational and Applied Mathematics, 234, 73-94 (2010) |
| [17] | Chen, T. and Strain, J. Piecewise-polynomial discretization and Krylov-accelerated multigrid for elliptic interface problems. Journal of Computational Physics, 227, 7503-7542 (2008) |
| [18] | Joshi, P. and Kumar, M. Mathematical model and computer simulation of three dimensional thin film elliptic interface problems. Computers & Mathematics with Applications, 63, 25-35 (2011) |
| [19] | Huang, H. and Li, Z. Convergence analysis of the immersed interface method. Journal of Numerical Analysis, 19, 583-608 (1999) |
| [20] | Beale, J. T. and Layton, A. T. On the accuracy of finite difference methods for elliptic problems with interfaces. Communications in Applied Mathematics and Computatioral Science, 1, 91-119 (2006) |
| [21] | Peaceman, D. W. and Rachford, H. H., Jr. The numerical solution of parabolic and elliptic differential equations. Journal of the Society for Industrial and Applied Mathematics, 3, 28-41 (1955) |
| [22] | Li, Z. and Mayo, A. ADI methods for heat equations with discontinuities along an arbitrary interface. American Mathematical Society, 48, 311-315 (1994) |
| [23] | Li, Z. and Soni, B. Fast and accurate numerical approaches for Stefan problems and crystal growth. Numerical Heat Transfer, Part B: Fundamentals, 35, 461-484 (1999) |
| [24] | Kandilarov, J. D. and Vulkov, L. G. The immersed interface method for two-dimensional heatdiffusion equations with singular own sources. Applied Numerical Mathematics, 57, 486-497 (2007) |
| [25] | Li, Z., Wang, D., and Zou, J. Theoretical and numerical analysis on a thermo-elastic system with discontinuities. Journal of Computational and Applied Mathematics, 92, 37-58 (1998) |
| [26] | Li, Z. and Ito, K. The immersed interface method: numerical solutions of PDEs involving interfaces and irregular domains. Society for Industrial and Applied Mathematics, 33, 119-167 (2006) |
| [27] | Osher, S. and Sethian, J. A. Fronts propagating with curvature-dependent speed: algorithms based on Hamilton-Jacobi formulations. Journal of Computational Physics, 79, 12-49 (1988) |
| [28] | Li, Z. and Lai, M. C. The immersed interface method for the Navier-Stokes equations with singular forces. Journal of Computational Physics, 171, 822-842 (2001) |
| [29] | Karaa, S. and Zhang, J. High order ADI method for solving unsteady convection-diffusion problems. Journal of Computational Physics, 198, 1-9 (2004) |
 2014, Vol. 35
2014, Vol. 35






































