Shanghai University
Article Information
- Ji-zeng WANG, Run-hua LI. 2014.
- Stretching strongly confined semiflexible polymer chain
- Appl. Math. Mech. -Engl. Ed., 35(10): 1233-1238
- http://dx.doi.org/10.1007/s10483-014-1862-9
Article History
- Received 2013-5-22;
- in final form 2013-12-19
Physical properties of biomacromolecules and biopolymers in complex microenvironments are usually influenced by external conditions such as geometrical confinements and applied forces [1] . Polymers in geometrical confinements that are smaller than their unconfined molecular sizes are of great significance in fields from polymeric liquid crystals to biological structures including cytoskeleton,stress fibres,nucleosomes,and viruses [1,2,3,4,5,6,7,8,9] . However,since the governing equations of these problems are very complex in mathematics,most theoretical studies are just based on scaling discussions,among which,two well-known scaling regimes on nanotubeconfined polymer chains were given by de Gennes [3] and Odijk [4,9,10] . The de Genne regime is for the case that the confinement size is larger than the chain’s persistence length,whose corresponding scaling theory regards that the chain forms a series of spherical blobs that are comparable with the tube diameter. At the other extreme,the Odijk regime is for the case that the confinement size is much smaller than the chain’s persistence length. In this case,the confined chains fluctuate back and forth by the tube-wall,where a typical length scale called the Odijk deflection length is identified. For the intermediate confinements,Odijk [10] presented a scaling analysis on the statistics of long DNA chains confined in both nanochannels and nanoslits and pointed out that more regimes are needed besides the two extremes originally described by de Gennes and Odijk. This conclusion has been confirmed by Wang et al. [11] and most recently by Hsu and Binder [12] using Monte Carlo simulations. They found that there exist more transition regimes to link the de Genne and Odijk regimes. For the semiflexible polymer chain simultaneously subject to both geometrical and tensile constraints,studies on the quantitative force-extension relations of the chain are rare. As one of few exceptions,Wang and Gao [13] analytically derived the end-to-end extension of a semiflexible polymer chain under strong confinements of cirlular tubes in the Odijk regime by modeling the confinement effect as a quadratic potential. Based on the so-called Blob theory [3] in de Genne’s regime,Dai and Doyle [14] investigated the similarities and differences between effects of nanoslit constraint and tensile load on polymers.
In spite of the above progresses,our understanding on the mechanics of confined semiflexible polymer chains is still far from complete. According to this view,in this study,we intend to furnish a theoretical framework based on Odijk’s theory of confined polymer to analytically derive the force-extension relation of the semiflexible chains under various confinements including circular tubes,rectangular tubes and slits,and use Brownian dynamics (BD) simulations based on the generalized bead-rod (GBR) model [2,13,15,16,17] to verify the corresponding theoretical predictions. 2 Confinement vs. effective force
We consider a wormlike chain (WLC) with the persistence length p and the contour length
L (L  p) subject to a large tensile force ƒs
on its two ends. We denote the position,the
tangential vectors,and their vertical components along the chain’s contour as r,u,r⊥,and
u⊥,respectively. Wang and Gao
[13]
have derived the following relation:
p) subject to a large tensile force ƒs
on its two ends. We denote the position,the
tangential vectors,and their vertical components along the chain’s contour as r,u,r⊥,and
u⊥,respectively. Wang and Gao
[13]
have derived the following relation:
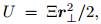 ,where
the potential strength Ξ depends on the geometrically constraining conditions. Following this
assumption,Wang and Gao
[13]
have further derived
By comparing Eqs. (1) and (2),we can obtain an effective force f
c induced by the geometrical
constraint
,where
the potential strength Ξ depends on the geometrically constraining conditions. Following this
assumption,Wang and Gao
[13]
have further derived
By comparing Eqs. (1) and (2),we can obtain an effective force f
c induced by the geometrical
constraint
In the Odijk regime,the confinement free energy of the chain can be given by
where a constant is omitted and λ is the so-called Odijk deflection length depending on the size of the confinement. Note that where θ = arccos(u(0) · u(λ )).Considering small undulation,we have
where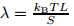 according to Eq. (4). Thus,the behavior of a strongly confined polymer chain
under stretching can be described by that of an unconfined chain subject to the effective force
equal to
according to Eq. (4). Thus,the behavior of a strongly confined polymer chain
under stretching can be described by that of an unconfined chain subject to the effective force
equal to 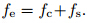 In other words,the confining effect of a nanochannel to a semiflexible polymer chain might be able to be viewed as the chain in a free solution subject to a stretching force.
The strength of the force depends on the size and the shape of the confinement. Eventually,
we can obtain the force-extension relation of a long WLC confined in nanochannels
[13,18]
where
In other words,the confining effect of a nanochannel to a semiflexible polymer chain might be able to be viewed as the chain in a free solution subject to a stretching force.
The strength of the force depends on the size and the shape of the confinement. Eventually,
we can obtain the force-extension relation of a long WLC confined in nanochannels
[13,18]
where 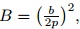 b is the bond length
[13,18]
,
b is the bond length
[13,18]
,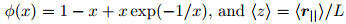 is
the normalized average distance between the two ends of the chain in the nanochannel.
is
the normalized average distance between the two ends of the chain in the nanochannel.
Figures 2(a)-2(c) show the schematic plot of the polymer chain,respectively,confined to a slit of height ds ,a rectangular tube with height d2 and width d1 ,and a capped circular tube with length l close to L and diameter dc . Based on the WLC model and our previous studies, we can derive the effective stretching force due to the confinements
For the slit confinement,c = 1.4,and For the rectangular tube,c = 1.10 [19,20] ,and For the capped circular tube,c = 2.36. We note that,the pre-factor c appearing in Eqs. (8)-(10) is a universal dimensionless parameter [19,20] ,which depends on the forms of confinements,but does not depend on the persistence length p and the confinement sizes ds,d1,d2 ,and dc . |
| Fig. 1 Schematic plot of polymer chain confined in various confinements |
 |
| Fig. 2 Comparisons of BD simulation results for relative extension of confined WLC with corresponding theoretical predictions based on concept of effective forces |
Numerical methods such as the BD simulation are viable to the above theoretical predictions,although efficiently realizing strong geometrical confinement can be challenging even for simulations. In this study,based on the powerful GBR model [2,15,16,17] ,BD simulations have been intensively performed for the chains confined in various nanochannels. In all the simulations,the chains are initially set in a straight configuration. Various confinements as shown in Figs. 1(a)-1(c) and constant tensile forces are then used during the chains’ relaxation. We record the normalized end-to-end distance of the chain along the z -axis at each time increment, and more than 10 different trajectories with different random seeds are averaged to obtain hz i.
From Figs. 2(a)-2(c),we can see that the theoretical predictions agree well with the BD simulations. Thus,we can conclude that the effect of geometrical confinements on the force-extension relation of a polymer can be represented by an effective force applied to an unconfined polymer chain.
| [1] | Reisner, W., Pedersen, J. N., and Austin, R. H. DNA confinement in nanochannels: physics and biological applications. Report on Progress in Physics, 75(10), 106601 (2012) |
| [2] | Wang, J. and Gao, H. A generalized bead-rod model for Brownian dynamics simulations of worm- like chains under strong confinement. The Journal of Chemical Physics, 123(8), 084906 (2005) |
| [3] | De Gennes, P. G. Scaling Concepts in Polymer Physics, Cornell University Press, New York (1979) |
| [4] | Odijk, T. Translational friction coefficient of hydrodynamically screened rodlike macromolecules. Macromolecules, 19(7), 2073-2074 (1986) |
| [5] | Schiessel, H. The physics of chromatin. Journal of Physics: Condensed Matter, 15(19), R699 (2003) |
| [6] | Earnshaw, W. C. and Harrison, S. C. DNA arrangement in isometric phage heads. nature, 268, 598-602 (1977) |
| [7] | Purohit, P. K., Kondev, J., and Phillips, R. Mechanics of DNA packaging in viruses. Proceedings of the National Academy of Sciences, 100(6), 3173-3178 (2003) |
| [8] | Wang, J., Li, L., and Gao, H. Compressed wormlike chain moving out of confined space: a model of DNA ejection from bacteriophage. Acta Mechanica Sinica, 28(4), 1219-1226 (2012) |
| [9] | Odijk, T. The statistics and dynamics of confined or entangled stiff polymers. Macromolecules, 16(8), 1340-1344 (1983) |
| [10] | Odijk, T. Scaling theory of DNA confined in nanochannels and nanoslits. Physical Review E, 77, 060901 (2008) |
| [11] | Wang, Y., Tree, D. R., and Dorfman, K. D. Simulation of DNA extension in nanochannels. Macromolecules, 44(16), 6594-6604 (2011) |
| [12] | Hsu, H. P. and Binder, K. Semi-flexible polymer chains in quasi-one-dimensional confinement: a Monte Carlo study on the square lattice. Soft Matter, 9(44), 10512-10521 (2013) |
| [13] | Wang, J. and Gao, H. Stretching a stiff polymer in a tube. Journal of Materials Science, 42, 8838-8843 (2007) |
| [14] | Dai, L. and Doyle, P. S. Comparisons of a polymer in confinement versus applied force. Macromolecules , 46, 6336-6344 (2013) |
| [15] | Wang, J., Fan, X., and Gao, H. Stretching short DNAs in electrolytes. Molecular and Cellular Biomechanics, 3(1), 13-19 (2006) |
| [16] | Wang, J. and Gao, H. Brownian dynamics simulations of charged semiflexible polymers confined to curved surfaces. Journal of the Mechanical Behavior of Biomedical Materials, 4(2), 174-179 (2011) |
| [17] | Liu, B., Wang, J., Fan, X., Kong, Y., and Gao, H. An effective bead-spring model for polymer simulation. Journal of Computational Physics, 227, 2794-2807 (2008) |
| [18] | Kierfeld, J., Niamploy, O., Sa-Yakanit, V., and Lipowsky, R. Stretching of semiflexible polymers with elastic bonds. European Physical Journal E, 14(1), 17-34 (2004) |
| [19] | Burkhardt, T. W. Free energy of a semiflexible polymer in a tube and statistics of a randomly- accelerated particle. Journal of Physics A: Mathematical, Nuclear and General, 30(7), L167-L172 (1997) |
| [20] | Yang, Y., Burkhardt, T.W., and Gompper, G. Free energy and extension of a semiflexible polymer in cylindrical confining geometries. Physical Review E, 76(1), 011804 (2007) |
 2014, Vol. 35
2014, Vol. 35












