Shanghai University
Article Information
- R. R. BHARGAVA, K. JANGID. 2014.
- Strip-coalesced interior zone model for two unequal collinear cracks weakening piezoelectric media
- Appl. Math. Mech. -Engl. Ed., 35(10): 1249-1260
- http://dx.doi.org/10.1007/s10483-014-1890-9
Article History
- Received 2013-8-9;
- in final form 2014-4-1
Piezoelectric ceramics have been extensively used in hi-tech instruments such as sensors, actuators,and transducers. Theoretical investigation to understand cracking behavior has been done by Parton[1],Cherepanov[2],Deeg[3],Zhang et al.[4],et al. Pak[5] obtained the closed form solution for an anti-plane fracture problem for cracked unbounded piezoelectric media. Pak[6] further studied the influence of the electric fields on the fracture behavior of piezoelectric ceramics using the method of distribution dislocation and electric dipoles. Suo et al.[7] discussed the crack problem in a piezoelectric ceramic under poled and unpoled conditions, and investigated the stress field near the crack tip in piezoelectric ceramic using the complex potential formulation. Experimentally,Tobin and Pak[8] showed that the crack growth along the direction perpendicular to the poling axis was enhanced when the applied electric field was in the same direction as the poling,and retarded if it was applied opposite to the poling direction. For many Perovskite-type ceramic deform appreciably under electric fields,it is observed that these fracturs are under electric loading. This phenomenon was theoretically investigated by Yang and Suo[9]. Huo et al.[10] studied a multilayered ceramic actuator. Gong and Suo[11] further gave a non-linear finite element simulation for the reliability of multilayer ceramic actuators.
Ru et al.[12] studied the electric-field induced interfacial cracking in multilayer electrostrictive actuators for small-scale saturation for an interface crack lying between an electrode layer and ceramic matrix.
Sosa[13] modelled the effect of the electric field on the crack arrest and crack skewing for a two-dimensional piezoelectric ceramic to understand the effect of electric yielding. Gao et al.[14] proposed a strip-saturation model for a finite crack perpendicular or parallel to the poling axis of poled piezoelectric medium with electric polarization reaching a saturation limit along a line segment in the front of the crack. Jeong et al.[15] analyzed the problem of a crack in a ferroelectric ceramic with perfect saturation under electric loading.
A simplified electric-displacement saturation model for an impermeable crack in a piezoele- ctric has been given by many researchers such as Fulton and Gao[16],Gao et al.[14],andWang[17].
Much fewer studies were reported in the literature on the analysis of two collinear cracks in piezoelectric ceramics. Zhou et al.[18] studied the behavior of two collinear cracks weakening a piezoelectric layer bonded to two half-spaces under anti-plane shear loading using the Fourier transform and the integral equation technique. Li[19] analyzed the problem of two collinear equal transversely situated cracks in a long narrow piezoelectric ceramic strip. Two collinear unequal cracks problem for a poled piezoelectric plate subject to remotely applied combined in-plane mode-I electromechanical loads was investigated by Li and Lee[20]. Lu et al.[21] addressed the problem of two semi-infinite collinear cracks in a piezoelectric strip using the complex variable technique and the conformal mapping.
As far as we know,Bhargave and Jangid[22, 23] were the first to propose respective strip- yield and strip-saturation for two collinear equal cracks weakening a piezoelectric medium under mode-I electromechanical loadings.
In the present paper,we focus on a mathematical strip-saturation model with coalesced interior saturation zones of two unequal collinear hairline straight cracks weakening a poled and transversely isotropic piezoelectric plate. The paper is organized as follows. The problem is mathematically formulated in Section 2. Section 3 presents the solution to the problem. Applications of the model proposed are presented in Section 4. Expressions are derived in this section for the developed saturation zones,the crack opening displacement (COD),the stress intensity factor (SIF),and the local energy release rate (LERR). Section 5 illustrates a case study for poled and transversely isotropic PZT-5H plate to investigate the effect of prescribed loadings on the SIF,the COD,and the LERR. Section 6 concludes the results obtained and discusses the applicability of the proposed model. 2 Statement of problem
A poled transversely isotropic piezoelectric plate occupies the entire x1x2-plane with the polling direction along the x2-axis. The plate is cut along two unequal-collinear hairline straight cracks. L1 and L2 (assuming L1 > L2) occupy the intervals [d,c] and [b,a] on the x1-axis, respectively. The unidirectional normal uniform constant stress σ22 = σ22∞ and the electrical- displacement D2 = D2∞ are prescribed at the remote boundary of the plate. Consequently, the cracks are opened in a self-similar fashion forming a strip-saturation zone ahead of each tip of the two cracks. The prescribed loads are increased to the limit such that the developed saturation zones at the interior tip of the two cracks get coalesced. Thus,three developed saturation zones are denoted by Γ1,Γ2,and Γ3,which occupy intervals [d2,d],[c,b],and [a,a1] on the x1-axis,respectively. To stop the crack from further opening by electric polarization,the developed saturation zones are subjected to the in-plane normal and cohesive saturation-limit electric-displacement D2 = Ds. Schematically,the configuration of the problem is depicted in Fig. 1.
 |
| Fig. 1 Schematic presentation of problem |
The physical boundary conditions may mathematically be written as

The desired solution Φ,1 to Eq. (A9) in Appendix A is uniquely determined under the above boundary conditions. 3 Solution to problem
The continuity of Φ,1(x1) on the whole real axis implies that
According to Eq. (A17) in Appendix A,its solution may be written as The boundary condition (v) together with Eq. (A9) in Appendix A leads to the following vector Hilbert problem: Introducing a new complex function vector Ω(z) = (Ω1 Ω2 Ω3 Ω4)T asΩ(z) = HRBF(z),
which together with Eq. (2) yields the relation
where Λ = [HR]-1,HR = 2ReY ,and Y = iAB-1.The second and fourth components of Eq. (3) in terms of potentials Ω2(z) and Ω4(z) yield the following scalar Hilbert problems:
Eliminating Ω4(x1) from the above equations,one can obtain The solution to Eq. (7) may be written using Eq. (A16) in Appendix A as where X1(z),P1(z),etc. are given in Appendix B.To obtain Ω4(z),Eq. (6) is rewritten using the boundary condition (iv) as
Using Eq. (A16) in Appendix A,the solution to Eq. (9) can be written as where P2(z),X2(z),etc. are given in Appendix B. 4 ApplicationsThe expressions are derived in this section for the lengths of the developed saturation zones at the exterior tips of the two cracks,the COD,the SIF,and the LERR. 4.1 Lengths of saturation zones
The electric-displacement D2(x1) may be determined using
Taking the fourth component of Eq. (11),substituting the required values from Eq. (10),and finally simplifying it,one obtains
The respective lengths of the saturation zones at the tips x1 = d of the crack L1 and x1 = a of the crack L2 can be calculated by extending Dugdale’s hypothesis[27] for electric-displacement to remain finite at every point of the crack. We obtain the following nonlinear equation at
and at x1 = a1, The unknowns d1 and a1 are calculated by approximately solving Eqs. (13) and (14). 4.2 CODThe relative opening of the crack faces,Δu2(x1),is determined using
Substituting the value of Ω2(z) from Eq. (8) and integrating it,one obtains where the symbol Δ indicates the difference between the values on the upper and lower crack surfaces,and S3,S4,etc. are given in Appendix B. 4.3 SIFThe open mode SIFs (KI(·)) at the crack tips x1 = d,c,b,and a are,respectively,defined as
Substituting σ22(x1) from Eq. (A9) in Appendix A,Eq. (4),and Eq. (8) into the above equa- tions and simplifying,we obtain It may be noted that KI(·) are dependent on the prescribed mechanical and electrical loads, the material constants,and the lengths of the cracks. 4.4 LERRThe energy release rate can be calculated using the J-integral
 where γ is a contour enclosing the crack tip,starting from any point on the lower crack surface
and terminating at any point on the upper crack surface,and h = 1/2 (σij
γij − DiEi) is the
electric enthalpy per unit volume.
where γ is a contour enclosing the crack tip,starting from any point on the lower crack surface
and terminating at any point on the upper crack surface,and h = 1/2 (σij
γij − DiEi) is the
electric enthalpy per unit volume.
Calculating the integral on vanishingly small contours at the crack tips x1 = d,x1 = c, x1 = b,and x1 = a,one obtains the LERRs,respectively,as
where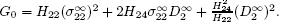 5 Case study
5 Case study
As an illustration,the results obtained above are used to a cracked poled PZT-5H ceramic plate to study the effect of the crack length and the prescribed mechanical and electric loads on the SIF and the LERR. The material constants recapitulated in Table 1 for PZT-5H are taken from Ou and Wu[28].
The prescribed mechanical tension is σ22∞=10 MPa,the electric-displacement is D2∞ = 0.003 C/m2,and the lengths of the cracks are L1 = 2a01=5 mm and L2 = 2a02=4 mm, till otherwise specified. 5.1 Effect on saturation zone length
Figure 2 shows that as the prescribed electric-displacement load is increased,the bigger saturation zone develops at the outer tip of the longer crack. The above variation is plotted for different ratios of bigger to smaller crack length. It may be noted that when two cracks are equal,the biggest saturation zone develops. The reverse effect is seen,i.e.,a smaller saturation zone develops as the shorter crack becomes smaller,as compared to bigger crack.
 |
| Fig. 2 Normalized saturation zone length at outer tip of bigger crack versus electric load ratio (D2∞/Ds) |
Figure 3 depicts the development of saturation zone at the exterior tip of the shorter crack as the prescribed electrical-displacement load is increased. It is emphasized that when the two cracks are of equal lengths,the developed saturation zone repeats the same variation similar to that in Fig. 2 for the saturation zone for equal crack lengths. It is interesting to note that at the exterior crack tip,much smaller saturation zone develops as compared to that seen at the exterior tip of the bigger crack,when bigger to smaller crack length ratio is taken as 1/2 ,1/3 ,1/4 , and 1/5 .
 |
| Fig. 3 Normalized saturation zone length at outer tip of smaller crack versus electric load ratio (D2∞/Ds) |
The variation of the LERR versus smaller crack length is plotted in Fig. 4 at the tips a,b,c, and d of the two cracks,which shows a linear increase in the LERR at all four tips. Also,it is noted that the LERR is higher at the interior tips b and c than that at the corresponding exterior tips d and a of the cracks. The LERR shows a steep increase at the tips of the smaller crack vis-a-vis that at the tips of the bigger crack. The points at which the LERR curves intersect are the cases when two cracks L1 and L2 are equal,which also confirms the correctness of the model proposed.
 |
| Fig. 4 LERR versus crack length ratio a02/a01 |
It may be noted from Fig. 5 that the LERR shows a shallow parabolic increase as the prescribed tension σ22∞ is increased from zero to 107 N/m2 at the tips a,b,c,and d of the cracks. The LERRs at the interior tips b and c of the two cracks are higher than those corresponding to the outer tips a and d. Consequently,the zones developed at the interior tips are more liable to get coalesced.
 |
| Fig. 5 LERR versus prescribed mechanical load σ22∞ |
The effect of the electric-displacement load on KI(·) is studied taking it as the non-dimensional electric loading factor λd (= (c33/e33)(D2∞ /σ22∞)),where σ22∞=10 MPa.
Figure 6 depicts a fan like linear variation in KI(·) for increasing values of λd. These are in agreement with the experimental findings for negative electric displacement loading,all the KI(·) predict an shielding effect on crack growth. For positive electric displacement loading, KI(·) predict an unshielding effect.
 |
| Fig. 6 SIFs versus prescribed electric-displacement load |
(i) The strip-saturation model proposed for two unequal collinear cracks with a coalesced interior saturation zone is a viable model.
(ii) The effect of electric-displacement loading on the saturation zone length shows that the model is capable of crack growth arrest.
(iii) Also,the effect of electric-displacement loading on SIFs validates the results obtained using the proposed model.
Acknowledgement The authors gratefully acknowledge the discussion and encouragement given by Prof. R. D. Bhargava (Senior Professor and Head (retired),Indian Institute of Technology Bombay, Mumbai) during course of this work. The second author is thankful to ministry of Human Resource Development for the financial support. Appendix A
The appendix is recapitulated from Refs. [17] and [24] to make the paper self-sufficient. As well-known,in a rectangular coordinate system xi (i = 1,2,3),the constitutive equations for the stress components σij and the electric displacement component Di (i,j = 1,2,3) and the gradient equations may be expressed as
and the equilibrium equations for the stresses and the electric-displacement in absence of body force and electric charge,respectively,can be written as where ui,φ,γ ij,and Ei denote the displacement,the electric potential,the strain,and the electric field, respectively. cijkl,ekij,and εkij stand for the elastic,the piezoelectric,and the dielectric constants, respectively.Introduce a generalized displacement vector u (defined in Ref. [25]) as
where superscript T denotes the transpose of the matrix,f(x1 + px2) is an analytic function,p is a complex number,and a is a constant four element column vector. Equations (A1)-(A3) satisfy Eq. (A4) for an arbitrary f(x1 + px2) if which has non-trivial solution only if where the matrices W,R,and Q are given by Let the eight roots of Eq. (A6) be denoted by pα and pα. The conditions of positive definiteness of the strain energy and the electrical energy densities give that pα is not real. To determine pα,the following standard eigen-equations are solved:
where
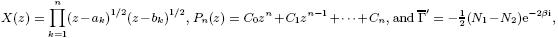 According to the Stroh formulation,the general solution satisfying Eqs. (A1)-(A3) may be written
as
According to the Stroh formulation,the general solution satisfying Eqs. (A1)-(A3) may be written
as
In addition,the matrices A and B have the following nature:
where I is a 4 × 4 unit matrix. The generalized stress function Φ is such that According to Muskhelishvili[26] ,the stress component σ22 can be expressed in terms of two complex potentials Ψ(z) and χ(z) as The Hilbert problem for a plate occupying the Ox1x2-plane and cut along n-collinear straight cracks Li (i = 1,2,· · · ,n),with end points ai and bi lying on the Ox1-axis and the rims of the cracks are subjected to the uniform constant stress σ22. Then,Eq. (A12) yields Under the assumption lim ψ(t + ix2) = 0,where t is any point on Li. The superscripts + and − denote the value of the function as it is approached from x2 > 0 or x2 < 0,respectively. Rearranging Eq. (A13),the following dual Hilbert problems are obtained: Using Muskhelishvili[26] ,the solution to Eqs. (A14) and (A15) may be written as where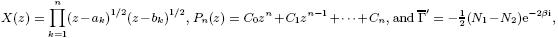 in which N1 and N2 are the values of principle stresses prescribed at infinity,and β is the angle between
N1 and the Ox1-axis. The constant C0 is determined using the boundary condition at infinity,and the
constants Ci (i = 1,2,· · · ,n) are determined using the condition of single-valuedness of displacements
on crack rims.
Appendix B
where F(k),E(k),and ∏(α2,k) are the complete elliptic integrals of the first,the second,and the third
kind,respectively.
where sn u,cn u,and dn u are the Jacobian elliptic functions.
where F(φ',k),E(φ',k),and ∏(φ',α2,k) are the incomplete elliptic integrals of the first,the second,and
the third kinds,respectively.
in which N1 and N2 are the values of principle stresses prescribed at infinity,and β is the angle between
N1 and the Ox1-axis. The constant C0 is determined using the boundary condition at infinity,and the
constants Ci (i = 1,2,· · · ,n) are determined using the condition of single-valuedness of displacements
on crack rims.
Appendix B
where F(k),E(k),and ∏(α2,k) are the complete elliptic integrals of the first,the second,and the third
kind,respectively.
where sn u,cn u,and dn u are the Jacobian elliptic functions.
where F(φ',k),E(φ',k),and ∏(φ',α2,k) are the incomplete elliptic integrals of the first,the second,and
the third kinds,respectively.
| [1] | Parton, V. Z. Fracture mechanics of piezoelectric materials. Acta Astronautica, 3, 671-683 (1976) |
| [2] | Cherepanov, G. P. Invariant г-integrals and some of their applications in mechanics. Journal of Applied Mathematics and Mechanics, 41, 397-410 (1977) |
| [3] | Deeg, W. F. The Analysis of Dislocation Crack and Inclusion Problems in Piezoelectric Solids, Ph.D. dissertation, Stanford University, Stanford (1980) |
| [4] | Zhang, T. Y., Zhao, M. H., and Tong, P. Fracture of piezoelectric ceramics. Advances in Applied Mechanics, 38, 148-289 (2002) |
| [5] | Pak, Y. E. Crack extension force in a piezoelectric material. ASME Journal of Applied Mechanics, 57, 647-653 (1990) |
| [6] | Pak, Y. E. Linear electro-elastic fracture mechanics of piezoelectric materials. International Journal of Fracture, 54, 79-100 (1992) |
| [7] | Suo, Z., Kuo, C. M., Barnett, D.M., andWillis, J. R. Fracture mechanics for piezoelectric ceramics. Journal of the Mechanics and Physics of Solids, 40, 739-765 (1992) |
| [8] | Tobin, A. C. and Pak, Y. E. Effect of electric fields on fracture behavior of PZT ceramics. Proceedings of SPIE, Smart Structures and Materials, 78 (1993) DOI 10.1117/12.148506 |
| [9] | Yang, W. and Suo, Z. Cracking in ceramic actuators caused by electrostriction. Journal of the Mechanics and Physics of Solids, 42, 649-663 (1994) |
| [10] | Hao, T. H., Gong, X., and Suo, Z. Fracture mechanics for the design of ceramic multilayer actua- tors. Journal of the Mechanics and Physics of Solids, 44, 23-48 (1996) |
| [11] | Gong, X. and Suo, Z. Relaibility of ceramic multilayer actuators: a nonlinear finite element sim- ulation. Journal of the Mechanics and Physics of Solids, 44, 751-769 (1996) |
| [12] | Ru, C. Q., Mao, X., and Epstein, M. Electric-field induced interfacial cracking in multilayer electrostrictive actuators. Journal of the Mechanics and Physics of Solids, 46, 1301-1318 (1998) |
| [13] | Sosa, H. On the fracture mechanics of piezoelectric solids. International Journal of Solids and Structures, 29, 2613-2622 (1992) |
| [14] | Gao, H., Zhang, T. Y., and Tong, P. Local and global energy release rates for an electrically yielded crack in a piezoelectric ceramic. Journal of the Mechanics and Physics of Solids, 45, 491-510 (1997) |
| [15] | Jeong, K. M., Kim, I. O., and Beom, H. G. Effect of electric displacement saturation on the stress intensity factor for a crack in a ferroelectric ceramic. Mechanics Research Communications, 31, 373-382 (2004) |
| [16] | Fulton, C. C. and Gao, H. Effect of local polarization switching on piezoelectric fracture. Journal of the Mechanics and Physics of Solids, 49, 927-952 (2001) |
| [17] | Wang, T. C. Analysis of strip electric saturation model of crack problem in piezoelectric materials. International Journal of Solids and Structures, 37, 6031-6049 (2000) |
| [18] | Zhou, Z. G., Wang, B., and Cao, M. S. Two collinear anti-plane shear cracks in a piezoelectric layer bonded to dissimilar half spaces. European Journal of Mechanics A/Solids, 20, 213-226 (2001) |
| [19] | Li, X. F. Closed-form solution for a piezoelectric strip with two collinear cracks normal to the strip boundaries. European Journal of Mechanics A/Solids, 21, 981-989 (2002) |
| [20] | Li, X. F. and Lee, K. Y. Two collinear unequal cracks in a poled piezoelectric plane: mode I case solved by a new approach of real fundamental solutions. International Journal of Fracture, 165, 47-60 (2010) |
| [21] | Lu, Z. X., Liu, P., and Guo, J. H. Exact solutions of two semi-infinite collinear cracks in piezo- electric strip. Applied Mathematics and Mechanics (English Edition), 32(11), 1399-1406 (2011) DOI 10.1007/s10483-011-1510-9 |
| [22] | Bhargava, R. R. and Jangid, K. Strip-saturation model for piezoelectric plane weakened by two collinear cracks with coalesced interior zones. Applied Mathematical Modelling, 37, 4093-4102 (2012) |
| [23] | Bhargava, R. R. and Jangid, K. Strip electro-mechanical yielding model for piezoelectric plate cut along two equal collinear cracks. Applied Mathematical Modelling, 37, 9101-9116 (2013) |
| [24] | Qin, Q. H. Fracture Mechanics of Piezoelectric Materials, WIT Press, Southampton (2001) |
| [25] | Barnett, D. M. and Lothe, J. Dislocation and line charges in anisotropic piezoelectric insulators. Physica Status Solidi (B), 67, 105-111 (1975) |
| [26] | Muskhelishvili, N. I. Some Basic Problems of the Mathematical Theory of Elasticity, Nordhoff, The Netherlands (1963) |
| [27] | Dugdale, D. S. Yielding of steel sheets containing slits. Journal of the Mechanics and Physics of Solids, 8, 100-104 (1960) |
| [28] | Ou, Z. C. and Wu, X. On the crack-tip stress singularity of interfacial cracks in transversely isotropic piezoelectric biomaterials. International Journal of Solids and Structures, 40, 7499-7511 (2003) |
 2014, Vol. 35
2014, Vol. 35






































