Shanghai University
Article Information
- A. HASSAN, Tian-su SONG. 2014.
- Dynamic anti-plane analysis for two symmetrically interfacial cracks near circular cavity in piezoelectric bi-materials
- Appl. Math. Mech. -Engl. Ed., 35(10): 1261-1270
- http://dx.doi.org/10.1007/s10483-014-1891-9
Article History
- Received 2013-5-20;
- in final form 2014-5-7
2 College of Aerospace and Civil Engineering, Harbin Engineering University, Harbin 150001, P. R. China
Due to electro-mechanical coupling response of piezoelectric materials,they have wide ap- plications in modern science technology. For instance,the piezoelectric materials have played important roles in the design and health monitoring of ship and marine structures as sensors, actuators,power supplies,etc. Occasionally,newly developed piezoelectric devices acquire frac- ture or failure,because their brittleness and faults occur during their manufacturing,polling process,and service procedures. Therefore,researchers paid great attention to the failure be- haviors caused by defects in those devices.
In recent years,cracks located in piezoelectric arrangements have been studied. Meguid and Wang[1] examined theoretically the dynamic interaction between two cracks in a piezoelectric medium under incident anti-plane shear wave loading. Then,Wang[2] investigated the dynamic behavior of interacting interfacial permeable cracks in two piezoelectric media. Also,Zhao and Meguid[3] studied the dynamic behavior of a piezoelectric laminate containing multiple interfacial collinear cracks under steady-state electro-mechanical loads. Zhong and Li[4] gave a closed-form analytical solution to the collinear anti-plane shear cracks lying at the mid-plane of a piezoelectric strip and solved the problem at the inner and outer crack tips. Ma et al.[5] studied the transient response of piezoelectric bi-materials under a dynamic anti-plane concentrated force or electric charge with a perfectly bonded interface. Zhao et al.[6] solved the case of the scattering shearing wave (SH-wave) from an interface cylindrical elastic inclusion with a semicircular disconnected curve by the suitable Green’s function.
Mueller et al.[7] proposed in intensive simulations an efficient non-hyper singular traction boundary integral equation method (BIEM) for anti-plane dynamic problems of piezoelectric solids with cracks or/and holes. In case of functionally graded piezoelectric solids,they also performed in-plane crack analysis under time-harmonic loading by the BIEM[8]. Recently,Shin and Lee[9] analyzed the dynamic propagation of a crack in a functionally graded piezoelectric material interface layer between two dissimilar piezoelectric layers under anti-plane shear using integral transform approaches.
In some cases,there exist complicated defects like cracks emanating from a circular cavity. Guo et al.[10] studied the scattering and the dynamic stress intensity factor (DSIF) of the SH-wave by interface cylindrical elastic inclusion with diametrical cracks. Wang and Gao[11] analyzed the stress intensity factor of the mode III fracture of edge cracks originating from a circular hole in piezoelectric solid media.
The goal of this paper is to investigate theoretically the influence on the DSIFs in trans- versely isotropic piezoelectric bi-materials with two symmetrically interfacial cracks near the edges of a circular cavity,subjected to the dynamic incident anti-plane SH-wave. An available theoretical method to the dynamic analysis in the related research field is provided. The emphasis is placed on the stress intensity factors at the inner and outer tips of the left crack. The formulations are based on Green’s function method,and the boundary value problems are solved with the conjunction and crack-simulation technique. The boundary conditions for the defects are assumed to be traction free and electrically permeable. 2 Constitutive equations
The model consists of two transversely isotropic semi-infinite piezoelectric media MI and MII. The isotropic plane lies in the X1X2-plane,and the polling direction is along the positive X3-axis. Two symmetrically interfacial cracks are presented near the edges of a circular cavity and subjected to the displacement out-of-plane and the electric field in-plane components. Figure 1 shows the model dimensions,where R0 is the radius of the circular cavity,A is the length of the crack,and B is the distance between the edge of the cavity and the inner tip of the crack.
 |
| Fig. 1 Piezoelectric bi-materials with symmetrically interfacial cracks near edges of circular cavity |
The time-harmonic and two-dimensional field can be expressed by the following equation:
where A* describes the desired field variable,and ω is the incident wave frequency. The time independent variable A(X1,X2) will be accounted in all the following equations neglecting the exponential form e−iωt for the sake of convenience[1, 3].Taking into account the absence of body forces and free charges,the equilibrium equations of the piezoelectricity for the dynamic incident SH-wave are
where c44,e15,and κ11 are the shear elastic modulus,the piezoelectric constant,and the dielec- tric constant of the piezoelectric medium,respectively; while w,φ,and ρ are the displacement out of plane,the electric potential,and the mass density of the medium,respectively. In terms of the column coordinate system (r,θ),where ξ = reiθ centered at the origin-O,as shown in Fig. 1,the anti-plane shear stress components (γrz and γθz) and the in-plane electric displacement components (Dr and Dθ) for a piezoelectric solid can be expressed as Solving Eqs. (2) and (3),when c44κ11 +e2 15 ≠ 0,the results are the Helmholtz equation and the Laplace equation as follows: where g is a constant.These equations describe the electro-mechanical behavior of a homogeneous piezoelectric material under anti-plane mechanical and in-plane electrical loading[2]. k is the wave number defined by
and μ is the effective piezoelectric stiffness. The relation between the electric potential and the displacement out of plane is given by 3 Boundary conditionsConsider a well bonded piezoelectric bi-material subjected to the dynamic incident SH-wave directed with an angle α0 in Medium MI,with the existence of two symmetrically interfacial cracks near the edges of a circular cavity. The boundary conditions of the two cracks and the cavity are assumed to be traction free and electrically permeable.
Using superscripts I,II,and c to express variables in Medium MI,Medium MII,and the circular cavity,respectively,the boundary conditions can be detailed as follows:
(i) At the cracks,
where r ∈ [R0 + B,R0 + B + A],and θ = 0,π.(ii) At the cavity,
where |r| ∈ R0.(iii) At the well-bonded interfaces of the two semi-infinite media,the electro-elastic fields are continuous. 4 Green’s functions
The fundamental solutions of the elastic displacement Gw and the electric potential Gφ for a semi-infinite piezoelectric medium with a semi-circular notch under the dynamic incident SH-wave at an arbitrary point |r0| > R0 on the surface X2 = 0 can be expressed as[10]
where Hm(1) is the Hankel function of the first kind. In the semi-circular notch,Green’s function Gφc is The coupled Green’s functions Gw and Gφ consist actually of two parts,i.e.,incidence and scattering[12]. The unknown constants Am,Bm,and Cm can be achieved by the boundary conditions. 5 Dynamic electro-elastic fieldsThe piezoelectric bi-materials are subjected to the dynamic incident SH-wave directed with an angle α0 in Medium MI. Figure 2 shows the reflected and refracted waves caused by the interface between the two media.
 |
| Fig. 2 Reflected and refracted waves caused by interface between two media |
Due to different impedances at the interface joining the piezoelectric bi-materials,scattering fields occur[6]. The dynamic electro-elastic fields and the corresponding scattering fields can be detailed as follows[12].
The incident elastic displacement w(i) and the incident electric potential φ(i) are
and the corresponding scattering fields w(is) and φ(is) are The reflected elastic displacement w(r) and the refracted electric potential φ(r) are and the corresponding scattering fields w(rs) and φ(rs) are The refracting elastic displacement w(f) and the refracting electric potential φ(f) are and the corresponding scattering fields w(fs) and φ(fs) areNote that w2 = w0 + w1 and φ2 = φ0 + φ1 lead to kI cos α0 = kII cos α2 [2]. Summation of the total electro-elastic fields is
for Medium MI and Medium MII,respectively. Finally,only the electric field exists in the circular cavity,which can be expressed as All the unknown constants can be solved by returning to the boundary conditions. 6 Integral equationBefore calculating the DSIFs,the integral equation must be established by the conjunction and crack-simulation technique. Figure 3 shows conjunction for the piezoelectric bi-materials with two semi-circular notches.
 |
| Fig. 3 Conjunction for piezoelectric bi-materials with two semi-circular notches |
The two semi-infinite media are separated at the interface X2 = 0,bearing in mind the absence of the cracks. To overcome this and achieve the assumption of traction free and electric permeable cracks,a pair of negative shear stresses −γI θz and −γII θz are applied on the surfaces of MI and MII at the cracks’ locations as shown in Fig. 3. The continuity conditions of the shear stresses can be expressed as[10, 12]
where r0 ∈ [R0,R0 + B] or r0 > R0 + B + A,and θ0 = 0,π. A pair of additional forces f1(r0,θ0) and f2(r0,θ0) are applied at the well-bonded interfaces of the two semi-infinite media to satisfy the continuity conditions of elastic displacements,which can be expressed as in whichwhere


By solving the equations above,the integral equation to calculate the unknown force f1(r0,θ0) can be obtained through conjunction of the two semi-infinite parts as follows:
7 Calculation of DSIFs After calculating the integral equation and getting the unknown force f1(r0,θ0),the dimen- sionless DSIFs (kσ 3 ) at the inner and outer tips of the left crack can be defined as where the characteristic parameter Q is equal to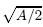 ,and τ0 = kIw0μ1 refers to the shear
stress magnitude of the incident wave[10].
8 Numerical examples and analysis
,and τ0 = kIw0μ1 refers to the shear
stress magnitude of the incident wave[10].
8 Numerical examples and analysis
In this section,the numerical examples are provided using the FORTRAN language program to show the effect of different parameters. Based on the results governed by Eq. (23),some numerical results for the DSIFs at the inner and outer tips of the left crack are plotted to show the influence of the physical parameters,the structural geometry,and the frequencies of the incident wave on the DSIFs.
First,a comparison of the DSIFs at the outer tip of the left crack (ξ2) between the present paper model and the document[12] model is shown in Fig. 4. It can be noticed that the curves are changed in the same manner with the increase in the wave number at MI. However,they did not coincide quit well. In the current paper,although the distance B is very small (B/R0 = 0.001), it still exists as a separation between the cracks and the cavity,which indicates that depending on the geometry of the medium,the relation between the cracks and the cavity is altered causing the changes happen to the values of the DSIFs.
 |
| Fig. 4 Comparison of DSIFs between two models under vertical incidence |
Figure 5 shows the variations of the DSIFs at the inner (ξ1) and outer (ξ2) tips of the left interfacial crack with different distances (B) between the edge of the cavity and the inner tip of the crack. It can be seen that the DSIF is larger for the outer tip (about 30%) than that for the inner tip. At the two tips,the DSIFs decrease with the increase in B at the range kIR0 = 0-1.8. The outer tip shows the increase in the DSIFs when reaching the value kIR0 = 2.4 for about 20% and then continue to decrease,while the inner tip shows some slight increase at the same value. As examples,the value B/R0 = 0.6 is considered at the next calculating results.
 |
| Fig. 5 Variations of DSIFs at inner and outer tips of left crack with kIR0 for different B/R0 |
Figure 6 shows the oscillations of the DSIFs at ξ1 and ξ2 with different incident wave frequencies (λI). The outer tip gives the larger values of DSIFs than the inner tip (about 30%). At both the tips,the DSIFs are smaller at higher incident wave frequencies for kIR0 = 0-1.2, and for higher kIR0 values,the situation is reflected. Then,the DSIFs continue to decrease after the value kIR0= 2.4.
 |
| Fig. 6 Variations of DSIFs at inner and outer tips of left crack with kIR0 for different λI |
Figure 7 shows the variations of the DSIFs with different wave numbers kI at the two tips ξ1 and ξ2. The curves are swaying more for the higher wave number than those for the lower one. The oscillation phenomenon of DSIFs is more significant at higher wave number kI. The oscillation phenomenon appears clearly at the outer tip.
 |
| Fig. 7 Variations of DSIFs at inner and outer tips of left crack with A/R0 for different kIR0 |
At Fig. 8,the variation with different crack lengths A is shown. The increase in the wave number kI leads to the decrease in the DSIFs. The curves are swaying more for the percentage (A/R0 > 1.0),and then the oscillation phenomenon appears at both the tips.
 |
| Fig. 8 Variations of DSIFs at inner and outer tips of left crack with kIR0 for different A/R0 |
A theoretical analysis is investigated to show the influence on the DSIFs in transversely isotropic piezoelectric bi-materials with two symmetrically permeable interfacial cracks near the edges of a circular cavity,subjected to the dynamic incident anti-plane SH-wave. The comparison between the present paper and previous work illustrates that depending on the geometry of the medium,the relation between the cracks and the cavity is altered causing the changes happen to the DSIFs. The increase in the distance between the cavity and the cracks decreases the DSIFs. The outer tip in the left crack gives the larger values of DSIFs than the inner one. Higher frequencies lead to lower DSIFs for the low level of wave number. The oscillation phenomenon of DSIFs should be taken into consideration,especially for the higher wave number of the incident medium and also if the crack length is longer than the cavity radius. The crack-simulation technique can be used for analyzing the piezoelectric bi-materials with more complicated interfacial defects and for the design and health monitoring of ship and marine structures.
| [1] | Meguid, S. A. and Wang, X. D. Dynamic antiplane behavior of interacting cracks in a piezoelectric medium. International Journal of Fracture, 91, 391-403 (1998) |
| [2] | Wang, X. D. On the dynamic behavior of interacting interfacial cracks in piezoelectric media. International Journal of Solids and Structures, 38, 815-831 (2001) |
| [3] | Zhao, X. H. and Meguid, S. A. On the dynamic behavior of a piezoelectric laminate with multiple interfacial collinear cracks. International Journal of Solids and Structures, 39, 2477-2494 (2002) |
| [4] | Zhong, X. C. and Li, X. F. Closed-form solution for two collinear cracks in a piezoelectric strip. Mechanics Research Communications, 32, 401-410 (2005) |
| [5] | Ma, C. C., Chen, X. H., and Ing, Y. S. Theoretical transient analysis and wave propagation of piezoelectric bi-materials. International Journal of Solids and Structures, 44, 7110-7142 (2007) |
| [6] | Zhao, J. X., Qi, H., and Su, S.W. Scattering of SH-wave from interface cylindrical elastic inclusion with a semicircular disconnected curve. Applied Mathematics and Mechanics (English Edition), 29(6), 779-786 (2008) DOI 10.1007/s10483-008-0609-1 |
| [7] | Mueller, R., Gross, D., Rangelov, T., and Dineva, P. Dynamic fracture of piezoelectric solids with defects. Procedia Engineering, 10, 76-81 (2011) |
| [8] | Dineva, P., Gross, D., Muller, R., and Rangelov, T. Time-harmonic crack problems in functionally graded piezoelectric solids via BIEM. Engineering Fracture Mechanics, 77, 1101-1115 (2010) |
| [9] | Shin, J. W. and Lee, Y. S. Anti-plane moving crack in a functionally graded piezoelectric layer between two dissimilar piezoelectric strips. Journal of Mechanical Science and Technology, 26(4), 1017-1025 (2012) |
| [10] | Guo, J., Qi, H., and Xu, Q. Z. Scattering of SH-wave by interface cylindrical elastic inclusion with diametrical cracks. World Conference on Earthquake Engineering (14th), Mira Digital Publishing, Saint Louis (2008) |
| [11] | Wang, Y. J. and Gao, C. F. The mode III cracks originating from the edge of a circular hole in a piezoelectric solid. International Journal of Solids and Structures, 45, 4590-4599 (2008) |
| [12] | Song, T. S. and Li, D. Dynamic stress intensity factor for interfacial cracks of mode III on a circular cavity in piezoelectric bimaterials (in Chinese). Chinese Journal of Theoretical and Applied Mechanics, 42(6), 1219-1224 (2010) |
 2014, Vol. 35
2014, Vol. 35

























