1 Introduction

The researches on the nonholonomic dynamics have important theoretical value and noticeable sense for applications. Remarkable advance has been achieved ^{[1, 2, 3, 4, 5, 6, 7, 8]} . Also,a lot of results on the form invariance and conserved quantity for mechanical systems have been obtained ^{[9, 10, 11, 12, 13, 14, 15, 16, 17, 18]} . The weakly nonholonomic system (WNS) is a special one whose constraint equations contain a small parameter. When the small parameter equals 0,the system becomes a holonomic system (HS). Mei ^{[19, 20, 21]} studied the equations of motion and approximate solutions,the canonical transformation,and the stability for the WNS,respectively. Following Refs. [19]-[21],we work on its form invariance and the relevant conserved quantity. First,the differential equations of motion are established for a WNS. Second,the definition and the criterion of form invariance of the system are given. Finally,the condition under which the form invariance leads to a conserved quantity and the form of conserved quantity are presented. 2 Differential equations of motion for WNS

Assume that the position of a mechanical system is determined by the n generalized coordinates q _s(s = 1,2,· · · ,n),and its motion is subject to the g ideal bilateral linear homogeneous nonholonomic constraints

where β =1,2,· · · ,g ; σ =1,2,· · · ,ε; ε = n − g; s = 1,2,· · · ,n, and µ is a small parameter. When µ = 0,the constraint equations (1) become holonomic. The differential equations of motion of the system can then be expressed as where L = L(q,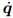,t) is the Lagrangian,Q_s = Q_s(q,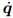,t) are non-potential generalized forces, and λ_β are undetermined multipliers. 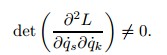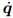Suppose that the system is nonsingular,namely, Then,from (1) and (2),one can solve λ_β as functions of q,,t,and µ,and (2) can be rewritten as which are called the HS equations corresponding to the WNS (1) and (2),where are the generalized constraint forces. It can be proved that the solution to the corresponding HS (3) gives the motion of the WNS,if the initial conditions of motion satisfy (1). In order to discuss the approximate solution to the WNS,we expand the generalized constraint forces Λ_s as a power-series in the parameter µ as follows: Then,we get the first degree approximation of (3) Also,all generalized accelerations can be solved from (3),written as and from (6),they can be written as 3 Definition and criterion of form invariance

Choose the infinitesimal transformations for the group of time and coordinates as follows:

where ε is an infinitesimal parameter,ξ₀and ξ_s are the generating functions of the infinitesimal transformations. Suppose that the dynamical functions L,Q_s,Λ_s,and f_βbecome L^*,Q^*_s,Λ^*_s,and f^*_β,respectively,after the infinitesimal transformation (9). Then,we have where

Definition 1 If the form of equations keeps invariant when the dynamical functions are replaced by the corresponding transformed ones,respectively,then such invariance is called form invariance. According to the definition,the form invariance for equations of motion (3) is

where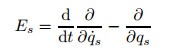 are Euler operators. The form invariance for constraint equations (1) is Substituting (10) into (12),neglecting the terms of ε 2 and higher order terms,and using (3),we obtain Similarly,in the above,replacing (12) and (3) by (13) and (1),respectively,we get Also,for the first degree approximate equations (6),we have

Criterion 1 For the HS (3) corresponding to the WNS (1) and (2),if the infinitesimal generators ξ₀ and ξ_s satisfy (14),then the relevant invariance is a form invariance of the system.

Criterion 2 For the WNS (1) and (2),if the infinitesimal generators ξ ₀ and ξ_s satisfy (14) and (15),then the relevant invariance is a form invariance of the system.

Criterion 3 For the first degree approximate HS (6) corresponding to the WNS (1) and (2),if the infinitesimal generators ξ₀ and ξ_s satisfy (16),then the relevant invariance is a form invariance of the system.

Criterion 4 For the first degree approximate system of the WNS (1) and (2),if the infinitesimal generators ξ₀ and ξ_s satisfy (16) and (15),then the relevant invariance is a form invariance of the system. 4 Conserved quantity deduced from form invariance

Based on the theory of form invariance for general nonholonomic systems (NSs) ^[22] ,the form invariance for WNSs can also lead to a conserved quantity.

Proposition 1 If the infinitesimal generators ξ₀ and ξ_s are ones of form invariance for the corresponding HS (3) and there exists a gauge function G_F = G_F (q,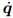,t,µ) satisfying the structure equation

where then the form invariance can lead to the conserved quantity

Proof First,we have

Then,using Criterion 1,we know that the above formula is zero. Similarly,one can prove the following Propositions 2−4.

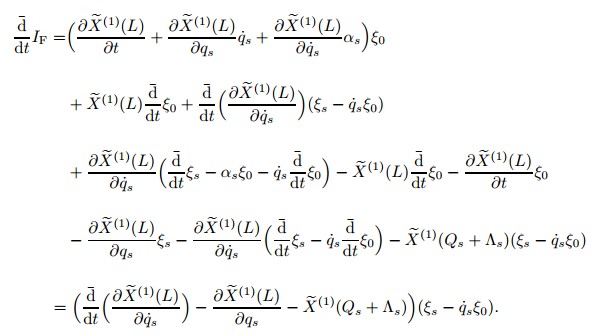
Proposition 2 If the infinitesimal generators ξ₀ and ξ_s are ones of form invariance for the WNS (1) and (2) and there exists a gauge function G_F = G_F (q,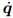,t) satisfying the structure equation (17),then the form invariance can lead to the conserved quantity (19).

Proposition 3 If the infinitesimal generators ξ₀ and ξ_s are ones of form invariance for the first degree approximate HS (6) and there exists a gauge function G_F = G_F (q,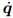,t,µ) satisfying the structure equation

where then the form invariance can lead to the conserved quantity (19).

Proposition 4 If the infinitesimal generators ξ₀ and ξ_s are ones of form invariance for the first degree approximate system of the WNS and there exists a gauge function G_F = G_F (q,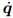,t,µ) satisfying the structure equation (20),then the form invariance can lead to the conserved quantity (19).

Making use of the above propositions,one can obtain the conserved quantities deduced from the form invariance for WNSs. 5 Illustrative example

In the following,we give an example to illustrate the application of the above results.

A WNS is

Discuss its form invariances and their corresponding conserved quantities.

From (2),we can get

From (3),we can obtain Also,(8) presents The criterion equation (14) for form invariance shows Then,we can find its solution which is relevant to the form invariance for the corresponding HS (23) Taking the calculation,we have Substituting (25) and (26) into the structure equation (17),we then obtain GF = −t. The conserved quantity (19) gives From (15),we have One can see that generators (25) do not satisfy (28),namely,they are not the ones of form invariance for the WNS. For the first degree approximate system (24),the criterion equations (16) show One can find the following solutions: which are generators of form invariance for the first degree approximate HS. Using generators (29) or (30) and taking the calculation,we get Substituting (29) and (31) into the structure equation (20),we then obtain GF = −t. Similarly,substituting (30) and (31) into the structure equation (20),we have GF = −t. The conserved quantity (19) then gives which are conserved quantities for the first degree approximate system. Taking the derivatives of (32) and (33) with respect to the time t according to (23),we obtain Therefore,they are approximate conserved quantities of the original system. 6 Conclusions

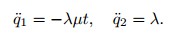
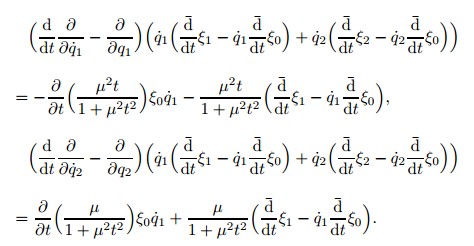
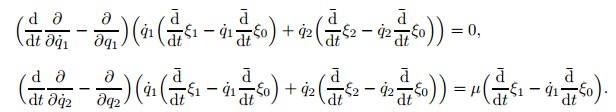
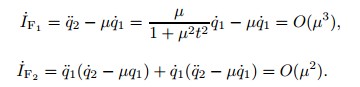
For mechanical systems,the study on the form invariance and the conserved quantity deduced from it is more complex than those of Noether symmetry and Noether conserved quantity. Especially for NSs,including WNSs,there are more restrictions to their form invariance than those of the corresponding HSs. Also,for deducing conserved quantities from the form invariance,the structure equation must be satisfied. However,in respect of finding the conserved quantity,sometimes we only need to discuss the form invariance and conserved quantity for the corresponding HSs,because the motion of an NS is in the solutions of the corresponding HS.