Shanghai University
Article Information
- T. HAYAT, S. ABELMAN, M. HAMESE. 2014.
- Oscillatory Couette flow of rotating Sisko fluid
- Appl. Math. Mech. -Engl. Ed., 35(10): 1301-1310
- http://dx.doi.org/10.1007/s10483-014-1865-9
Article History
- Received 2013-3-4;
- in final form 2013-10-2
2. Department of Mathematics, Faculty of Science, King Abdulaziz University, Jeddah 21589, Saudi Arabia;
3. Centre for Differential Equations, Continuum Mechanics and Applications, School of Computational and Applied Mathematics, University of the Witwatersrand, Johannesburg 2050, South Africa
Rheological fluids have wide coverage in medicine,engineering,and industry. For example,they are important in polymeric and food processes. Further,non-Newtonian electrically conducting fluids in a rotating system are significant in geophysical,cosmical,and astrophysical applications. The Couette flow configuration for rotating frame and porous space has a growing interest among recent modelers and computer scientists. This is in fact because of the occurrence of such flows in petroleum,magnetohydrodynamic (MHD) generators,geothermal processes,underground energy,and metallurgical processes. It is a well-established argument that stretching,bearing,and fluid-driven shear play a key role in synovial joints. Nalim et al.[1] examined the oscillatory Couette flow mechanical shear loader to simulate in vitro fluiddriven shear. This flow configuration generates shear since the loader enhances understanding of mechanotransduction in the joint tissue. Prasad and Kumar[2] implemented a boundary layer assumption for the analysis of MHD oscillatory Couette flow with a porous space. The Laplace transform method was used for the velocity field in the flow of a viscous fluid. The hydromagnetic Couette flow of viscous fluid in a rotating channel was investigated by Beg et al.[3, 4] . The lower plate of the channel exhibited non-torsional oscillation. Seth et al.[5, 6] and Guria et al. [7] addressed MHD Couette flows in a porous channel and rotating frame.
It is now known that non-Newtonian fluids are more suited in industrial and physiological applications than Newtonian fluids. The expressions for these fluids in a rotating frame are very complicated. Hence,numerical and analytical techniques are implemented to describe the flow of rheological materials by means of various aspects [8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40] . The purpose of the current work is to advance the knowledge in this area. Thus,a nonlinear problem for the MHD Couette flow of a Sisko fluid between two infinite non-conducting parallel plates in a rotating frame is formulated. The whole system is in a rotating frame of reference about an axis normal to the plates. While the lower plate is kept stationary,the oscillatory flow induced by the rotation of the upper plate is examined. This paper is structured in four sections. The fundamental equations and the mathematical model are given in Section 2. Section 3 comprises the numerical study and discussion,while Section 4 synthesizes conclusions. 2 Problem formulation
An incompressible MHD Sisko fluid is considered between two infinite non-conducting parallel plates at z = 0 and z = d. A constant magnetic field B0 acts in the z -direction,with the z -axis perpendicular to the plates. The whole system is in a state of rigid body rotation with a uniform angular velocity (0,0,Ω). Figure 1 shows a cross section of the geometry of the problem.
 |
| Fig. 1 Physical sketch and geometry of problem |
The equations relevant to the present flow configuration can be written as
Here,V denotes the velocity,ρ is the fluid density,t is the time,σ is the electrical conductivity, and the modified pressure
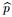 including the centrifugal force term is defined as follows:
where p is the pressure. S is
Oscillatory Couette flow of rotating Sisko fluid 1303
in which a and b are material constants,and tr is the trace of the matrix. The expression for
A1is
including the centrifugal force term is defined as follows:
where p is the pressure. S is
Oscillatory Couette flow of rotating Sisko fluid 1303
in which a and b are material constants,and tr is the trace of the matrix. The expression for
A1is
Note that Eq. (4) is immediately recognizable for a power law fluid when a = 0. Equation (4) holds for a viscous fluid. We denote the velocity components by (u,v,w). Since we are dealing with infinitely long parallel plates,all physical quantities except the pressure are functions of z and t. The incompressibility condition gives w = 0. The velocity field V is expressed by the following expression:
This definition of velocity satisfies Eq. (1) identically. Utilizing Eqs. (2)-(6) results in the following scalar equations:and
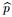 is independent of z .
The subjected conditions are
Here,ω denotes the oscillating frequency of the upper plate and fluid,and ǫ is a constant. It
may be easily verified that Eqs. (7) and (8),after eliminating the modified pressure gradient,
satisfy the following equation:
where
and
Introduce
1304 T. HAYAT,S. ABELMAN,and M. HAMESE
Then,the dimensionless problem after omitting the asterisks becomes
is independent of z .
The subjected conditions are
Here,ω denotes the oscillating frequency of the upper plate and fluid,and ǫ is a constant. It
may be easily verified that Eqs. (7) and (8),after eliminating the modified pressure gradient,
satisfy the following equation:
where
and
Introduce
1304 T. HAYAT,S. ABELMAN,and M. HAMESE
Then,the dimensionless problem after omitting the asterisks becomes
and the rotation parameter K,the oscillatory Reynolds number β,the Hartman number M , and the nonlinear viscosity parameter L are defined by Note that a and b are nonzero in Eq. (17). 3 Numerical results and discussion
MATLAB pdepe is used for the numerical solution to Eqs. (14)-(16).
In Fig. 2,we plot the fluid velocity profiles q for increasing the Hartman number M . The primary velocity u increases rapidly towards the upper plate for increasing the Hartman number and small β. The secondary velocity v increases only marginally between the two plates,going to zero at the upper plate. For large β,we see that as M increases,the primary velocity u initially increases relatively slow between the plates and then increases rapidly towards the upper plate,while the secondary velocity v remains almost zero.
 |
| Fig. 2 Plots of u (solid lines) and v (dashed lines) for different values of M when t = 5 |
Figure 3 depicts the velocity q through the increased rotation parameter K. The primary velocity u increases rapidly through large K and small β. However,v increases from the lower plate η = 0 and reaches zero at η = 1. In the vicinity of the upper plate,there exists an incipient flow reversal in the secondary flow direction. For large β,we see that as K increases, the primary velocity u initially increases relatively slow between the plates and then increases rapidly towards the upper plate. The results of v for small and large β are qualitatively similar. Oscillatory Couette flow of rotating Sisko fluid 1305
 |
| Fig. 3Plots of u (solid lines) and v (dashed lines) for different values of K when t = 5 |
In Fig. 4,we plot the fluid velocity with increasing values of the nonlinear viscosity parameter L. For small β,as L increases,the value of u increases rapidly,whereas v increases marginally between the plates and vanishes at η = 1.
 |
| Fig. 4 Plots of u (solid lines) and v (dashed lines) for different values of L when t = 5 |
For large β,we see that as L increases,u initially increases relatively slow between the plates and then increases rapidly towards the upper plate,while v remains almost zero.
Figure 5 displays q through the index n. For small β,u is the largest for the shear thickening case and the smallest for the Newtonian case,whereas v remains almost zero. For large β,the same phenomenon is observed,with u initially increasing relatively slow between the plates and then increasing rapidly towards the upper plate,while v remains almost zero.
 |
| Fig. 5Plots of u (solid lines) and v (dashed lines) for different values of n when t = 5 |
In Fig. 6,u increases rapidly for β = 500,while for larger values of β,it initially increases relatively slow between the plates and then increases rapidly near the upper plate,whereas v remains almost zero for increasing values of β. The presence of a porous medium increases the resistance to flow.
 |
| Fig. 6Plots of u (solid lines) and v (dashed lines) for different values of β when t = 5 |
In Fig. 7(a),the fluid velocity q for varying values of
 is plotted for β = 100 and K = 500,100,and 50. We observe that u and v show almost linear behaviours near η = 0 for
all values of
is plotted for β = 100 and K = 500,100,and 50. We observe that u and v show almost linear behaviours near η = 0 for
all values of  . Initially,near η = 0,both the fluid velocities u and v increase as
. Initially,near η = 0,both the fluid velocities u and v increase as  increases. Then,when
increases. Then,when  =5,at approximately η = 0.2,the primary velocity u decreases
and becomes smaller than the primary velocities for the other two cases as the fluid moves
1306 T. HAYAT,S. ABELMAN,and M. HAMESE
towards the upper oscillating plate. A similar occurence is visible for v when
=5,at approximately η = 0.2,the primary velocity u decreases
and becomes smaller than the primary velocities for the other two cases as the fluid moves
1306 T. HAYAT,S. ABELMAN,and M. HAMESE
towards the upper oscillating plate. A similar occurence is visible for v when
 = 5 at
approximately η = 0.1. For v,there is backflow as the fluid moves towards the upper plate. In
Fig. 7(b),a similar behaviour is observed for β = 500 and K = 2 500,500,and 250. We keep
the ratio
= 5 at
approximately η = 0.1. For v,there is backflow as the fluid moves towards the upper plate. In
Fig. 7(b),a similar behaviour is observed for β = 500 and K = 2 500,500,and 250. We keep
the ratio
 the same in both Figs. 7(a) and 7(b). In Figs 7(a) and 7(b),M = 5,n = 2,
t = 5,L = 1,and ε = 0.001.
the same in both Figs. 7(a) and 7(b). In Figs 7(a) and 7(b),M = 5,n = 2,
t = 5,L = 1,and ε = 0.001.
 |
| Fig. 7Plots of u (solid lines) and v (dashed lines) through K/β = Ω/ω when t = 5 |
In Fig. 8,we depict the surface plots for u and v when t ∈ [0,1] and η ∈ [0,5]. Other values of the parameters are β = 500,M = 5,K = 5,n = 2,L = 1,and ε = 0.001. For u,the fluid moves towards the upper oscillating plate,while v remains relatively small between the plates. The periodicity of u is only slightly visible here as we have chosen ε= 0.001.
 |
| Fig. 8Surface plots for u and v when t ∈ [0,5],η ∈ [0,1],β = 500,M = 5,K = 5,n = 2,L = 1,and =ε 0.001 |
In Fig. 9,we depict the surface plots for u and v when t ∈ [0,5] and η ∈ [0,1]. Other values for the parameters are β = 500,M = 5,K = 5,n = 2,L = 1,and ε = 1. For u,the fluid moves towards the upper oscillating plate,while v remains relatively small between the plates. The periodicity of u is clearly visible here as we have chosen ε = 1.
 |
| Fig. 9Surface plots for u and v when t ∈ [0,5],η ∈ [0,1],β = 500,M = 5,K = 5,n = 2,L = 1,and ε = 1 |
The oscillatory Couette flow of MHD Sisko fluid between two infinite non-conducting parallel plates in a rotating frame is explored. The key findings of the presented analysis are listed below. 1308 T. HAYAT,S. ABELMAN,and M. HAMESE
(i) The conducted analysis of hydromagnetic Couette flow is significant in MHD power
generators,pumps,flow meters,nuclear reactors,biomagnetic fluid flows,and metallurgy.
(ii) Smaller Reynolds number β corresponds to the creeping flow.
(iii) The behaviour of the secondary fluid velocity v is oscillatory when the rotation parameter K increases.
(iv) The primary fluid velocity u is an increasing function of K.
(v) The secondary fluid velocity v exhibits a marginal change through K,and it remains
virtually the same for the increase in M ,L,n,and β.
Acknowledgements S. ABELMAN thanks the University of the Witwatersrand and the NRF,Pretoria,South Africa,for research funding. M. HAMESE was a Bachelor of Science Honours student in the School of Computational and Applied Mathematics,University of the Witwatersrand,Johannesburg in 2011. She contributed to this work through her Bachelor of Science Honours research project. The anonymous reviewers are thanked for their suggested corrections which lead to an improved manuscript
| [1] | Nalim, R., Pekkana, K., Sun, H. B., and Yokota, H. Oscillating Couette flow for in vitro cell loading. J. Biomech., 37, 939-942 (2004) |
| [2] | Prasad, B. G. and Kumar, R. Unsteady hydromagnetic Couette flow through a porous medium in a rotating system. Theor. Appl. Mech. Lett., 1, 042005 (2011) DOI 10.1063/2.1104205 |
| [3] | Bég, O. A., Ghosh, S. K., and Narahari, M. Mathematical modeling of oscillatory MHD Couette flow in a rotating highly permeable medium permeated by an oblique magnetic field. Chem. Engin. Commun., 198, 235-254 (2010) |
| [4] | Beg, O. A., Takhar, H. S., Zueco, J., Sajid, A., and Bhargava, R. Transient Couette flow in a rotating non-Darcian porous medium parallel plate configuration: network simulation method solutions. Acta Mech., 200, 129-144 (2008) |
| [5] | Seth, G. S., Ansari, M. S., and Nandkeolyar, R. Effects of rotation and magnetic field on unsteady Couette flow in a porous channel. J. Appl. Fluid Mech., 4, 95-103 (2011) |
| [6] | Seth, G. S., Hussain, S. M., and Singh, J. K. MHD Couette flow of class-II in a rotating system. J. Appl. Math. and Bioinformatics, 1, 31-54 (2011) |
| [7] | Guria, M., Das, S., Jana, R. N., and Ghosh, S. K. Oscillatory Couette flow in the presence of inclined magnetic field. Meccanica, 44, 555-564 (2009) |
| [8] | Greenspan, H. P. The Theory of Rotating Fluids, Cambridge University Press, Cambridge (1990) |
| [9] | Batchelor, G. K. An Introduction to Fluid Dynamics, 1st ed., Cambridge University Press, Cam- bridge (1967) |
| [10] | Fetecau, C., Fetecau, C., Kamran, M., and Vieru, D. Exact solutions for the flow of a generalized Oldroyd-B fluid induced by a constantly accelerating plate between two side walls perpendicular to the plate. Int. J. Non-Newtonian Fluid Mech., 156, 189-201 (2009) |
| [11] | Abbasbandy, S., Hayat, T., Ghehsareh, H. R., and Alsaedi, A. MHD Falkner-Skan flow of a Maxwell fluid by rotational Chebyshev collocation method. Appl. Math. Mech. -Engl. Ed., 34(8), 921-930 (2013) DOI 10.1007/s10483-013-1717-7 |
| [12] | Xu, M. and Liao, S. J. Laminar flow and heat transfer in the boundary layer of non-Newtonian fluids over a stretching flat sheet. Comp. Math. Appl., 57, 1425-1431 (2009) |
| [13] | Xue, C. F., Nie, J. X., and Tan, W. C. An exact solution of start up flow for the fractional generalized Burgers' fluid in a porous space. Nonlinear Anal. Theor. Meth. Appl., 69, 2086-2094 (2008) |
| [14] | Wang, S. W. and Tan, W. C. Stability analysis of double-diffusive convection of Maxwell fluid in a porous medium heated from below. Phys. Lett. A, 372, 3046-3050 (2008) |
| [15] | Zaimi, K., Ishak, A., and Pop, I. Stretching surface in rotating viscoelastic fluid. Appl. Math. Mech. -Engl. Ed., 34(8), 945-952 (2013) DOI 10.1007/s10483-013-1719-9 |
| [16] | Ariel, P. D. Two dimensional stagnation point flow of an elasto-viscous fluid with partial slip. Z. Angew. Math. Me. (ZAMM), 88, 320-324 (2008) |
| [17] | Cortell, R. Analysing flow and heat transfer of a viscoelastic fluid over a semi-infinite horizontal moving flat plate. Int. J. Non-Linear Fluid Mech., 43, 772-778 (2008) |
| [18] | Rajagopal, K. R. and Srinivas, A. R. On the development of fluid models of the differential type within a new thermodynamic framework. Mech. Res. Comm., 35, 483-489 (2008) |
| [19] | Hayat, T. Exact solutions to rotating flows of a Burgers' fluid. Comput. Math. Appl., 52, 1413-1424 (2006) |
| [20] | Ali, N., Hayat, T., and Asghar, S. Peristaltic flow of a Maxwell fluid in a channel with compliant walls. Chaos, Solitons and Fractals, 39, 407-416 (2009) |
| [21] | Hayat, T., Kara, A. H., and Momoniat, E. Travelling wave solutions to Stokes' problem for a fourth grade fluid. Appl. Math. Model, 33, 1613-1619 (2009) |
| [22] | Abelman, S., Momoniat, E., and Hayat, T. Steady MHD flow of a third grade fluid in a rotating frame and porous space. Nonlinear Anal.: Real World Appl., 10, 3322-3328 (2009) |
| [23] | Shahzad, F., Hayat, T., and Ayub, M. Stokes' first problem for the rotating flow of a third grade fluid. Nonlinear Anal.: Real World Appl., 9, 1794-1799 (2008) |
| [24] | Hayat, T., Khan, S. B., and Khan, M. The influence of Hall current on the rotating oscillating flows of an Oldroyd-B fluid in a porous medium. Nonlinear Dyn., 47, 353-362 (2007) |
| [25] | Hayat, T. and Abelman, S. A numerical study of the influence of slip boundary condition on rotating flow. Int. J. Comput. Fluid Dyn., 21, 21-27 (2007) |
| [26] | Abelman, S., Momoniat, E., and Hayat, T. Couette flow of a third grade fluid with rotating frame and slip condition. Nonlinear Anal.: Real World Appl., 10, 3329-3334 (2009) |
| [27] | Hayat, T., Khan, S. B., and Khan, M. Exact solution for rotating flows of a generalized Burgers' fluid in a porous space. Appl. Math. Model, 32, 749-760 (2008) |
| [28] | Hayat, T., Moitsheki, R. J., and Abelman, S. Stokes' first problem for Sisko fluid over a porous wall. Appl. Math. Comput., 217, 622-628 (2010) |
| [29] | Hayat, T., Nadeem, S., and Asghar, S. Hydromagnetic Couette flow of an Oldroyd-B fluid in a rotating system. Int. J. Eng. Sci., 42, 65-78 (2004) |
| [30] | Khan, M. and Farooq, J. On heat transfer analysis of a magnetohydrodynamic Sisko fluid through a porous medium. J. Porous Media, 13, 287-294 (2010) |
| [31] | Rani, H. P., Reddy, G. J., and Kim, C. N. Transient analysis of diffusive chemical reactive species for couple stress fluid flow over vertical cylinder. Appl. Math. Mech. -Engl. Ed., 34(8), 985-1000 (2013) DOI 10.1007/s10483-013-1722-6 |
| [32] | Hayat, T., Shehzad, S. A., and Alsaedi, A. Three-dimensional stretched flow of Jeffrey fluid with variable thermal conductivity and thermal radiation. Appl. Math. Mech. -Engl. Ed., 34(7), 823- 832 (2013) DOI 10.1007/s10483-013-1710-7 |
| [33] | Hayat, T., Abelman, S., Harley, C., and Hendi, A. Stokes' first problem for a rotating Sisko fluid with porous space. J. Porous Media, 15, 1079-1091 (2012) |
| [34] | Sajid, M. and Hayat, T. Series solution for steady flow of a third grade fluid through porous space. Trans. Porous Media, 71, 173-183 (2008) |
| [35] | Das, S., Maji, S. L., Guria, M., and Jana, R. N. Unsteady MHD Couette flow in a rotating system. Math. Comput. Model., 50, 1211-1217 (2009) |
| [36] | Hayat, T., Javed, M., and Ali, N. MHD peristaltic transport of a Jeffery fluid in a channel with compliant walls in porous space. Trans. Porous Media, 74, 259-274 (2008) |
| [37] | Abbas, Z., Wang, Y., Hayat, T., and Oberlack, M. Hydromagnetic flow in a viscoelastic fluid due to the oscillatory stretching surface. J. Nonlinear Mech., 43, 783-793 (2008) |
| [38] | Khan, M., Hayat, T., and Wang, Y. Slip effects on shearing flows in a porous medium. Acta Mech. Sin., 24, 51-59 (2008) |
| [39] | Hayat, T., Mambili-Mamboundou, H., Momoniat, E., and Mahomed, F. M. M. The Rayleigh problem for a third grade electrically conducting fluid in a magnetic field. J. Nonlinear Math. Phys., 15, Suppl. 1, 77-90 (2008) |
| [40] | [40] Gozde, S., Pakdemirli, M., Hayat, T., and Aksoy, Y. Boundary layer equations and Lie group analysis of a Sisko fluid. J. Appl. Math., 2012, 259608 (2012) |
 2014, Vol. 35
2014, Vol. 35



















