Shanghai University
Article Information
- G. S. SETH, S. M. HUSSAIN, S. SARKAR. 2014.
- Hydromagnetic oscillatory Couette flow in rotating system with induced magnetic field
- Appl. Math. Mech. -Engl. Ed., 35(10): 1331-1344
- http://dx.doi.org/10.1007/s10483-014-1868-9
Article History
- Received 2013-7-2;
- in final form 2014-3-8
2. Department of Mathematics, O. P. Jindal Institute of Technology, Raigarh 496109, India
Investigation of the problems of hydromagnetic flow of an electrically conducting fluid in a rotating environment assumes great significance owing to occurrence of different natural phenomena,which are induced by Coriolis and magnetic forces,and its application in several areas of astrophysics,geophysics,and fluid engineering,such as maintenance and secular variations of terrestrial magnetic field due to motion of Earth’s liquid core,internal rotation rate of the Sun, structure of rotating magnetic stars,turbo machines,magnetohydrodynamic (MHD) Ekman pumping,rotating MHD generators,and material processing. An order of magnitude analysis shows that the effects of Coriolis force are more pertinent than the inertial and viscous forces in hydromagnetic equations of motion in a rotating environment. Moreover,in magnitude,Coriolis and magnetic forces are comparable,and they together play a decisive role in characterizing hydromagnetic fluid flow problems in a rotating environment. Taking into account these facts, the unsteady hydromagnetic Couette flow in a rotating system was investigated by Chandran et al. [1] ,Singh et al. [2] ,Singh [3] ,Hayat et al. [4,5] ,Das et al. [6] ,Guria et al. [7] ,Seth et al. [8,9,10,11,12] , and Jha and Apere [13] to analyze various features of the problem. In the above studies,an induced magnetic field was neglected in comparison to the applied one. This supposition is valid because the magnetic Reynolds number is very small (Rm = 0.001−0.1) for metallic liquids and partially ionized fluids [14] . However,when the magnetic Reynolds number is equal to or greater than one,the effects of induced magnetic field become imperative in determining the flow features of the problem [15] . Observing this fact, Ghosh [16] studied the unsteady Hartmann flow in a rotating channel taking the induced magnetic field into account,where the fluid flow within the channel was induced due to periodic pressure gradient.
Our investigation is to study the hydromagnetic oscillatory Couette flow of an electrically conducting,viscous,and incompressible fluid in a rotating system in the presence of a uniform transverse magnetic field taking the induced magnetic field into consideration. The lower plate of the channel is assumed electrically non-conducting,while the upper plate is considered perfectly conducting. To the best of our knowledge,the solution obtained in the present study will be accounted in literature for the first time. Such a study may find application in turbo machineries and solidification process in metallurgy [13] . 2 Problem formulation and solution method
Consider the hydromagnetic oscillatory Couette flow of an electrically conducting,viscous, and incompressible fluid confined within two parallel plates z = 0 and z = l. The lower plate of the channel is electrically non-conducting,while the upper plate is perfectly conducting. The fluid flow within the channel is imbued by a uniform transverse magnetic field B0 which is applied in a direction parallel to the z -axis. Both the fluid and the channel rotate with the uniform angular velocity Ω about the z -axis. The fluid flow within the channel is induced due to non-torsional harmonic oscillations of the upper plate z = l in its own plane in the x-direction, while the lower plate z = 0 is kept stationary. The physical model of the problem is presented in Fig. 1. Since the plates of the channel are of infinite extent in the x- and y-directions,all physical quantities except pressure are functions of z and t only.
 |
| Fig. 1. Physical model of problem |
Under the assumptions made above,the governing equations of motion and magnetic induction for an electrically conducting,viscous,and incompressible fluid in a rotating environment reduce to
where u',v',B'x ,B'y ,ν ,µe ,ρ,νm,and p are the fluid velocity in the x-direction,the fluid velocity in the y-direction,the induced magnetic field in the x-direction,the induced magnetic field in the y-direction,the coefficient of kinematic viscosity,the magnetic permeability,the fluid density,the magnetic diffusivity,and the modified pressure including centrifugal force, respectively.The boundary conditions for the fluid velocity and the induced magnetic field are assumed to be where ω'
is the frequency of oscillations.In order to present Eqs. (1),(2),(4),and (5) along with the boundary conditions (6) and (7) in a non-dimensional form,the following non-dimensional quantities and parameters are introduced:
Equations. (1),(2),(4),and (5) with the use of dimensionless quantities and parameters defined in Eq. (8) are expressed in the following dimensionless form:
It is seen from Eqs. (9) and (10) that 2α2m measures the strength of the magnetic force relative to the Coriolis force. The boundary conditions (6) and (7),in a dimensionless form,are given by where ω = ω' /Ω is the frequency parameter.Equations (9)-(12) in a combined form are presented as
where ƒ = u + iv and b = Bx + iBy .The boundary conditions (13) and (14) in a compact form are expressed as
Since the fluid flow within the channel is induced due to harmonic oscillations of the upper plate η = 1 in the x-direction,the fluid velocity and the induced magnetic field are presumed in the following forms: where ƒ2 (η) and b2 (η) are the complex conjugates of ƒ1 (η) and b1 (η),respectively.Equations (15) and (16) with the help of Eq. (19) reduce to
The boundary conditions (17) and (18) with the help of Eq. (19) take the following forms: The exact solution to Eqs. (20)−(23) with the help of the boundary conditions (24) and (25) is obtained analytically,and the solution for the fluid velocity f (η,T ) and the induced magnetic field b (η,T ) is presented in the following form: where We shall now consider some particular cases of interest of the general solution (26) to (28k). 2.1 Case of vanishing magnetic Prandtl number (Pm→0)Setting Pm→ 0 in Eqs. (26) to (38),we obtain
Since the magnetic Reynolds number is very small in the case of vanishing magnetic Prandtl number Pm,the induced magnetic field b(η,T ) produced by the fluid motion is negligible in comparison to the applied one [14] .When ω is large and α2m) is of small order of magnitude i.e.,α2m) ~ O(1),the fluid flow becomes the boundary layer type. For the boundary layer flow near the oscillating plate η = 1, introducing the boundary layer coordinate ξ = 1 − η,we can obtain the expressions for the primary fluid velocity u(η,T ) and the secondary fluid velocity v (η,T ) from the solution (30) which are given by
where The asymptotic solutions (31) to (34) reveal the existence of two modes of oscillations in the flow field. These two modes correspond to the modified Stokes flow which are limited within thin boundary layers of thicknesses O (γ-11) and O (γ-13). These boundary layers may be recognized as hydromagnetic Stokes-Ekman boundary layers (Seth et al. [17] and Ansari et al. [18] ). It is noticed from Eqs. (33) and (34) that γ3-1ayer is thicker than γ1-1 ayer. The thickness of these boundary layers decreases with increasing either α2m) or ω or both,while it increases with increasing E.The exponential terms in the solutions (31) and (32) damp out quickly as ξ increases. When ξ > γ-13 ,i.e.,outside the boundary layer region,the solutions (31) and (32) reduce to
It is observed from Eq. (35) that there is no flow of fluid outside the hydromagnetic StokesEkman boundary layer region. It is worth mentioning here that in the limit of Pm→ 0, α2 and β2 tend to zero which implies that,for large ω,the thickness of α2 and β2 boundary layers,which may be acknowledged as magnetic diffusion boundary layers,tends to infinity implying thereby that the magnetic diffusion region extends up to the central line of the channel just as it happens in the limit ω → 0 and Pm6 = 0. 2.2 Case of small magnetic Prandtl number (Pm<1)It is revealed from the results reported in Section 2.1 in the case of vanishing magnetic Prandtl number and for large ω flow-field are divided into two regions: The hydromagnetic Stokes-Ekman boundary layer region and the spatially and temporally uniform region beyond the hydromagnetic Stokes-Ekman boundary layer region,i.e.,the magnetic diffusion region. Now,we consider more realistic situation in which the magnetic Prandtl number Pmis still smaller than unity but greater than zero.
From Section 2.1,it is clear that the magnetic diffusion region is always thicker than the hydromagnetic Stokes-Ekman boundary layer region. Therefore,for the case of interest,the magnetic diffusion region should be relatively inviscid (Benton and Loper [19] ). Keeping in view this fact,the expressions for α2 and β2 are obtained from the inviscid version of Eqs. (20) to (23) which are presented in the following forms:
Expanding the expressions for α1,β1,α2 ,and β2 in Eqs. (28a) and (28b) in powers of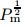 ,we
obtain
where
These expressions for α1
,β1,α2,and β2 are substituted in the solutions (26) and (27). The
coefficient functions in Eqs. (26) and (27) are expanded in powers of
,we
obtain
where
These expressions for α1
,β1,α2,and β2 are substituted in the solutions (26) and (27). The
coefficient functions in Eqs. (26) and (27) are expanded in powers of 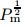 . When the terms only
up to
. When the terms only
up to 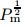 are retained,the resulting solutions are given by
where
When ω is large and α2m)~ O(1),the fluid flow in this case also becomes the boundary layer
type. For the boundary layer flow in the vicinity of oscillating plate η = 1,we obtain the velocity
and the induced magnetic field distributions from Eqs. (39) to (41),which are presented in the
following form:
where
are retained,the resulting solutions are given by
where
When ω is large and α2m)~ O(1),the fluid flow in this case also becomes the boundary layer
type. For the boundary layer flow in the vicinity of oscillating plate η = 1,we obtain the velocity
and the induced magnetic field distributions from Eqs. (39) to (41),which are presented in the
following form:
where
The asymptotic solutions (41) to (47b) present the existence of two modes of oscillations. These two modes of oscillations correspond to the modified Stokes flow,which are confined within thin boundary layers of thicknesses O (γ-11) ,O γ-13,and O (γ*-11) . Two out of these three boundary layers of thicknesses O (γ-11) and O (γ-13) may be identified as hydromagnetic Stokes-Ekman boundary layers,which are the same as those appearing near the oscillating plate of the channel in the case of vanishing magnetic Prandtl number and large ω.
Since αm is independent of the viscosity,it is noticed from the expressions in Eq. (46) that γ*1) and γ*2) are independent of the viscosity and depend only on the magnetic diffusivity. Therefore, γ*1) -boundary layer is named as the inviscid magnetic diffusion boundary layer. The thickness of this boundary layer decreases with increasing either ω or Pmor both,but increases with increasing either αm or E or both. It is found from Eqs. (33),(34),and (46) that the magnetic diffusion boundary layer is thicker than the hydromagnetic Stokes-Ekman boundary layers. The exponential terms in the solutions (42) to (45) damp out quickly as ξ increases. When ξ > γ*-11 ,i.e.,outside the magnetic diffusion boundary layer region,the solutions (42) to (45) assume the following forms:
It is interesting to note from the expressions in (48) that the region represented by ξ > γ* -11, i.e.,outside the magnetic diffusion region,is a current free zone in which there is no flow of fluid in the primary and secondary flow directions. It is observed from the cases reported in Sections 2.1 and 2.2 that the overall difference between the flow when Pm→ 0 and in the case Pm< 1 is that,in the later case,the magnetic diffusion region has a finite thickness which is confined within thin boundary layer of thickness O γ*-11. Also,there is a third region of the fluid flow beyond both the h ydromagnetic StokesEkman boundary layer region and the magnetic diffusion region. This outermost region is called the current free zone which extends up to the central line of the channel. However,in the former case,there exist two regions,i.e.,hydromagnetic Stokes-Ekman layer region and the magnetic diffusion region extending up to the central line of the channel. 2.3 Shear stress at plates and mass flow ratesThe dimensionless shear stresses τx and τy at the plates,due to the primary and secondary flows,respectively,are presented as
The dimensionless mass flow rates Qx and Qy in the primary and secondary flow directions, respectively,are given by 3 Results and discussionThe numerical values of the fluid velocity and the induced magnetic field,computed from the analytical solution (26) to (28k),are displayed graphically in Figs. 2 to 7 for different values of αm,E,and ω,considering ωT = π/2 and Pm= 0.7 (ionized hydrogen). It is noticed from Fig. 2 that both the primary and secondary fluid velocities decrease as αm increases. This implies that the magnetic field has a tendency to decelerate the fluid flow in both the primary and secondary flow directions. This trend of fluid velocity with respect to the magnetic field is in accord with the conventional property of magnetic field that the fluid flow of an electrically conducting fluid in the presence of magnetic field gives rise to a resistive force,known as the Lorentz force,which has a tendency to slow down fluid motion. It is perceived from Fig. 3 that both the primary and secondary fluid velocities increase as E decreases. Physically,the Ekman number signifies the ratio of the viscous force to the Coriolis force. Therefore,an increase in the Ekman number E leads to a decrease in the angular velocity Ω. This indicates that when the angular velocity increases,there is an increase in the fluid velocity in both the primary and secondary flow directions,i.e.,the rotation tends to accelerate fluid flow in both the primary and secondary flow directions. It is revealed from Fig. 4 that the primary fluid velocity increases,while the secondary fluid velocity decreases as the frequency parameter ω increases. This implies that oscillations tend to accelerate fluid flow in the primary flow direction,while they have a reverse effect on the fluid flow in the secondary flow direction. The reason is that the fluid flow within the channel is induced due to non-torisional oscillations of upper plate of the channel in the primary flow direction.
 |
| Fig. 2. Primary and secondary velocity profiles when E = 0.3 and ω = 3 |
 |
| Fig. 3. Primary and secondary velocity profiles when αm = 6 and ω = 3 |
 |
| Fig. 4. Primary and secondary velocity profiles when αm = 6 and E = 0.3 |
It is evident from Figs. 5 and 6 that the primary induced magnetic field decreases with increasing either αm or E in the regions near the stationary and oscillating plates of the channel, while the secondary induced magnetic field decreases with increasing either αm or E throughout the channel. This implies that the magnetic field tends to reduce the primary induced magnetic field in the regions near both plates of the channel,while the rotation has a reverse effect on it. The magnetic field has a tendency to reduce the secondary induced magnetic field throughout the channel,while the rotation has a reverse effect on it.
 |
| Fig. 5. Primary and secondary induced magnetic field profiles when E = 0.3 and ω = 3 |
 |
| Fig. 6. Primary and secondary induced magnetic field profiles when αm = 6 and ω = 3 |
It is revealed from Fig. 7 that the primary induced magnetic field increases in the region 0 6 η 6 0.8,while it decreases in the region 0.8 < η 6 1 with increasing ω. The secondary induced magnetic field decreases in the region near the stationary plate of the channel,while it increases in the region 0.4 6 η 6 1 as ω increases. This implies that oscillations tend to enhance the primary induced magnetic field in the region 0 6 η 6 0.8,while they have a reverse effect on the primary induced magnetic field in the region 0.8 < η 6 1. Oscillations tend to reduce the secondary induced magnetic field in the region near the stationary plate of the channel,while they have a reverse effect on the secondary induced magnetic field in the region 0.4 6 η 6 1. Also,it is noticed from Figs. 5 and 6 that the primary induced magnetic field changes its direction in the region near the oscillating plate of the channel.
 |
| Fig. 7. Primary and secondary induced magnetic field profiles when αm = 6 and E = 0.3 |
The numerical values of the primary shear stress τx and the secondary shear stress τy at the oscillating and stationary plates,computed from the analytical expressions (49) and (50), are presented in Tables 1 to 4 for various values of αm,E,and ω. Also,the numerical values of the primary mass flow rate Qx and the secondary mass flow rate Qy are calculated from the analytical expression (51) and exhibited in Tables 5 and 6 for various values of αm,E,and ω,taking ωT = π/2 and Pm= 0.7. It is noticed from Table 1 that both the primary shear stress at the oscillating plate,i.e.,τx |η=1 ,and the secondary shear stress at the oscillating plate,i.e.,τy |η=1 ,decrease in magnitude with increasing E. With an increase in αm,τx |η=1 decreases in magnitude,while τy |η=1 increases in magnitude,attains a maximum,and then decreases in magnitude when E = 0.3 and 0.5,and it increases in magnitude when E = 0.7. This implies that the rotation has a tendency to enhance both the primary and secondary shear stresses at the oscillating plate. The magnetic field tends to reduce primary shear stress at the oscillating plate,while it tends to enhance the secondary shear stress at the oscillating plate when E = 0.7. It is evident from Table 2 that both the primary shear stress at the stationary plate,i.e.,τx|η=0 ,and the secondary shear stress at the stationary plate,i.e.,τy |η=0 ,decrease as E increases. With an increase in αm,τx |η=0 increases,while τy |η=0 behaves in oscillatory manner when E = 0.3,and it decreases when E = 0.5 and 0.7. This implies that the rotation tends to enhance both the primary and secondary shear stresses at the stationary plate. The magnetic field tends to enhance the primary shear stress at the stationary plate,while it tends to reduce the secondary shear stress at the stationary plate,when E > 0.5. It is observed from Table 3 that τx |η=1 increases in magnitude with increasing ω. With an increase in ω,τy |η=1 decreases in magnitude,attains a minimum,and then increases when αm = 6. It decreases in magnitude when αm = 7,while it increases in magnitude,attains a maximum and then decreases in magnitude when αm = 8. This implies that oscillations tend to enhance the primary shear stress at the oscillating plate. Also,it is noticed from Table 3 that there may exist separation of flow at the oscillating plate with increasing ω when αm = 6 and E = 0.3 and with increasing αm when ω = 5 and E = 0.3.
It is revealed from Table 4 that τx |η=0 increases as ω increases. When ω increases,τy |η=0 decreases when αm = 6 and 7,while it behaves in an oscillatory manner when αm = 8. This implies that oscillations tend to enhance the primary shear stress at the stationary plate,while they have a reverse effect on the secondary shear stress at the stationary plate when αm 6 7.has a reverse effect on it. It is found from Table 6 that Qx increases with increasing ω,while it decreases when αm = 6 and it behaves in an oscillatory manner when αm = 7 and 8 with increasing ω. This implies that oscillations tend to enhance the primary mass flow rate,while they have a reverse effect on the secondary mass flow rate when αm = 6.
Significant findings of the present investigation are given below.
In the case of vanishing magnetic Prandtl number and large frequency parameter,there arise thin double hydromagnetic Stokes-Ekman boundary layers near the oscillating plate of the channel,while for small magnetic Prandtl number and large frequency parameter,there appear thin triple boundary layers adjacent to the oscillating plate of the channel. Two boundary layers are recognized as the hydromagnetic Stokes-Ekman boundary layer and the magnetic diffusion boundary layer. The magnetic field tends to reduce the primary induced magnetic field in the regions near both the plates of the channel,while the rotation has a reverse effect on it. The magnetic field has a tendency to reduce the secondary induced magnetic field throughout the channel,while the rotation has a reverse effect on it. The rotation has a tendency to enhance both the primary and secondary shear stresses at the oscillating plate,and the magnetic field tends to reduce the primary shear stress at the oscillating plate. The rotation tends to enhance both the primary and secondary shear stresses at the stationary plate,and the magnetic field tends to enhance the primary shear stress at the stationary plate. The rotation has a tendency to enhance both the primary and secondary mass flow rates,while the magnetic field has a reverse effect on them.
| [1] | Chandran, P., Sacheti, N. C., and Singh, A. K. Effect of rotation on unsteady hydromagnetic Couette flow. Astrophysics and Space Science, 202, 1-10 (1993) |
| [2] | Singh, A. K., Sacheti, N. C., and Chandran, P. Transient effects on magnetohydrodynamic Couette flow with rotation. International Journal of Engineering Sciences, 32, 133-139 (1994) |
| [3] | Singh, K. D. An oscillatory hydromagnetic Couette flow in a rotating system. Zeitschrift für Angewandte Mathematik und Mechanik (ZAMM), 80, 429-432 (2000) |
| [4] | Hayat, T., Nadeem, S., and Asghar, S. Hydromagnetic Couette flow of a Oldroyd-B fluid in a rotating system. International Journal of Engineering Sciences, 42, 65-78 (2004) |
| [5] | Hayat, T., Nadeem, S., Siddiqui, A. M., and Asghar, S. An oscillatory hydromagnetic nonnewtonian flow in a rotating system. Applied Mathematics Letters, 17, 609-614 (2004) |
| [6] | Das, S., Maji, S. L., Guria, M., and Jana, R. N. Unsteady MHD Couette flow in a rotating system. Mathematical and Computer Modelling, 50, 1211-1217 (2009) |
| [7] | Guria, M., Das, S., Jana, R. N., and Ghosh, S. K. Oscillatory Couette flow in the presence inclined magnetic field. Meccanica, 44, 555-564 (2009) |
| [8] | Seth, G. S., Jana, R. N., and Maiti, M. K. Unsteady hydromagnetic Couette flow in a rotating system. International Journal of Engineering Sciences, 20, 989-999 (1982) |
| [9] | Seth, G. S., Singh, R., and Mahto, N. Oscillatory hydromagnetic Couette flow in a rotating system. Indian Journal of Technology, 26, 329-333 (1988) |
| [10] | Seth, G. S., Ansari, M. S., and Nandkeolyar, R. Unsteady hydromagnetic Couette flow within porous plates in a rotating system. Advances in Applied Mathematics and Mechanics, 2, 286-302 (2010) |
| [11] | Seth, G. S., Ansari, M. S., and Nandkeolyar, R. Unsteady hydromagnetic Couette flow induced due to accelerated movement of one of the porous plates of the channel in a rotating system. International Journal of Applied Mathematics and Mechanics, 6, 24-42 (2010) |
| [12] | Seth, G. S., Ansari, M. S., and Nandkeolyar, R. Effects of rotation and magnetic field on unsteady Couette flow in a porous channel. Journal of Applied Fluid Mechanics, 4, 95-103 (2011) |
| [13] | Jha, B. K. and Apere, C. A. Time-dependent MHD Couette flow of rotating fluid with Hall and ion-slip currents. Applied Mathematics and Mechanics (English Edition), 33(4), 399-410 (2012) DOI 10.1007/s10483-012-1559-9 |
| [14] | Davidson, P. A. An Introduction to Magnetohydrodynamics, Cambridge University Press, Cambridge (2006) |
| [15] | Pantokratoras, A. Comment on "Combined heat and mass transfer by laminar mixed convection flow from a vertical surface with induced magnetic field". Journal of Applied Physics, 102, 076113 (2007) |
| [16] | Ghosh, S. K. Unsteady hydromagnetic flow in a rotating channel with oscillating pressure gradient. Journal of the Physical Society of Japan, 62, 3893-3903 (1993) |
| [17] | Seth, G. S., Ansari, Md. S., and Nandkeolyar, R. Unsteady Hartmann flow in a rotating channel with perfectly conducting walls. International Journal of Applied Mechanics and Engineering, 16, 1129-1146 (2011) |
| [18] | Ansari, M. S., Seth, G. S., and Nandkeolyar, R. Unsteady Hartmann flow in a rotating channel with arbitrary conducting walls. Mathematical and Computer Modelling, 54, 765-779 (2011) |
| [19] | Benton, E. R. and Loper, D. E. On the spin-up of an electrically conducting fluid, part 1, the unsteady hydromagnetic Ekman-Hartman boundary layer problem. Journal of Fluid Mechanics, 39, 561-586 (1969) |
 2014, Vol. 35
2014, Vol. 35






































