Shanghai University
Article Information
- Jian YU, Chao YAN, Rui ZHAO. 2014.
- Assessment of shock capturing schemes for discontinuous Galerkin method
- Appl. Math. Mech. -Engl. Ed., 35(11): 1361-1374
- http://dx.doi.org/10.1007/s10483-014-1875-7
Article History
- Received 2014-2-27;
- in final form 2014-5-6
In recent years,computational fluid dynamics (CFD) has made great advancement towards becoming a realistic tool in aeronautical and astronautical industries due to the developments of computer power and CFD methods. However,plenty of engineering practice indicates that as a numerical tool,CFD is still frequently subject to limitations such as accuracy,efficiency, and reliability. Higher-order methods have been considered as a promising strategy to relieve these limitations,and various higher-order schemes with compact stencils have been proposed, such as the discontinuous Galerkin (DG) method,the spectral difference method,and the spectral volume method. The DG method has received great focus for its minimal stencil,h/p adaptation flexibility,and parallel computation efficiency[1]. An important aspect with the DG method for solving conservation laws is shock capturing. Typical shock capturing strategies for the DG can be categorized into three classes,i.e.,the limiting procedure,the reconstruction method,and the artificial diffusivity method.
Shu[2] and Cockburn and Shu[3] used the total variation bounded (TVB) limiter to capture shocks. The TVB limiter is simple and efficient,but could easily destroy high-order accuracy of the DG. Biswas et al.[4] proposed higher order extensions of Cockburn and Shu’s method for 1D and 2D cases. Burbeau et al.[5] proposed a problem-independent limiter aimed to define a way of taking into account the high-order space discretization in limiting process. Krivodonova[6] further generalized the limiter of Ref. [4] to systematically reduce the order of accuracy based on the behavior of the higher-order solution derivatives.
Alternatively,Qiu and Shu[7] introduced the weighted essentially non-oscillatory (WENO) schemes to reconstruct the polynomials around discontinuities to suppress spurious oscillations. In order to retain the compactness of DG,a Hermite WENO (HWENO) scheme[8] was constructed as limiters for DG. Luo et al.[9] developed an HWENO-based limiter through taking advantage of the handily available and yet valuable derivatives information. For the methods using WENO/HWENO,one needs an indicator to identify cells containing discontinuities first. A systematic comparison of typical discontinuity indicators can be found in Ref. [10].
Another approach is the artificial diffusivity method,which captures shocks through adding diffusion terms explicitly to governing equations. Major focus is generally given on how to compute artificial diffusivity coefficients. Typical work have been conducted by Persson and Peraire[11],Hartman[12],Xin and Flaherty[13],Bassi et al.[14] and Barter[15],which can be categorized into three species,i.e.,basis function schemes,face residual schemes,and elemental residual schemes.
The objective of the present study is to provide a systematic evaluation of typical shock capturing schemes for the DG method. The remainder of the paper is organized as follows. First,the basic DG formulation and typical shock capturing schemes are described. Then, several test cases are performed using different shock capturing schemes,and the comparisons in terms of accuracy,robustness,dependence on empirical parameters,and capability for steady solutions are carried out. Finally,the paper ends with conclusions and recommendations. 2 DG formulation 2.1 Governing equations
The compressible Euler equations are
in which ρ is the density,u is the velocity vector,p is the static pressure,e is the internal energy,and δ represents the Kronecker tensor. The following equation of state is used: where γ is the ratio of the specific heats. 2.1.1 DG methodTo formulate the DG discretization method,(1)−(3) can be rewritten as
where q is the conservative state vector,and fc (q) is the inviscid flux vector. Denote qh as an approximate solution and νh as a piecewise polynomial test function. Then,(5) can be reformulated as in which n represents the outward unit normal vector on the faces of K. Let qh be expressed as where φlp(x,y) are the basis functions of the polynomials of degree p,and for the DG method, the basis function and the test function are the same. Then,(6) can be written as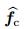 represents the Riemann solver to allow solution discontinuities at element interfaces. Here,
the Lax-Friedrich method is used for
represents the Riemann solver to allow solution discontinuities at element interfaces. Here,
the Lax-Friedrich method is used for 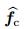 . For simplicity,(8) is rewritten as
where M is the mass matrix,and R(q) represents the residual vector. (9) is solved here using
the third order Runge-Kutta method[2] as follows:
3 Shock capturing schemes
. For simplicity,(8) is rewritten as
where M is the mass matrix,and R(q) represents the residual vector. (9) is solved here using
the third order Runge-Kutta method[2] as follows:
3 Shock capturing schemes
Here,we present the formulae of the shock capturing schemes,including the TVB limiter, the basis function-based (BF) scheme,the face residual-based (FR) scheme,and the element residual-based (ER) scheme. 3.1 TVB Limiter
The TVB limiter first defines a limiter function as follows:
where M is a user-specified constant,a1 is the linear part of the approximate solution in (7), and a2,a3,...,am are the differences of cell average values[16]. In this work,m is set to be 3 as only one-dimensional and quadrilateral elements are considered.The TVB limiter is applied after each Runge-Kutta stage through applying (11) to the approximate solution. For systems,the TVB limiter is used to characteristic variables to enhance robustness. 3.2 Artificial diffusivity schemes
Artificial diffusivity methods stabilize shocks through adding additional diffusivity terms to governing equations. For simplicity,the Laplace model is chosen here,and (8) can now be written as
The key now is how to calculate the artificial diffusivity coefficients εK. 3.2.1 BF schemeAccording to (7),we define  h as
h as

Cε and κ are user-specified constants,and hK represents the size of element K. 3.2.2 FR scheme
Define the jump on the cell interface as  = qL − qR,then
= qL − qR,then
For Riemann solvers,we have
Then,the discontinuity sensor sk is computed by where k = 1,2,· · · ,nc,and nc is the number of the system equations[14].The coefficient is calculated as follows:
where Cε is the user-specified constant.To improve the robustness of the method,we replace the computed artificial diffusivity coefficients εk with its maximum value on element K through the following equations:
Within the scope of this paper,the employment of (22) has caused little loss of solution accuracy. Note that the BF scheme in the above section also uses constant artificial diffusivity within each element. 3.2.3 ER scheme
Define the element residual as[12]
Also,we define  K as
K as
The coefficient is then calculated as
where Cε is a user-specified constant,and β is usually chosen to be 0.1. Note that the same modification as (22) is made here,and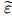 is finally used on element K.
4 Numerical results
is finally used on element K.
4 Numerical results
In this section,numerical experiments are performed to test the performance of the above shock capturing schemes. The test cases include the Sod problem,the Shu-Osher problem, the double Mach reflection problem,and the transonic NACA0012 flow. Detailed comparisons between the above shock capturing schemes in terms of resolution for discontinuity,accuracy, efficiency,robustness,and capability for steady solutions are given. 4.1 Sod problem
The initial condition is given by
The baseline grid consists of 100 uniform elements on the domain of [−5,5]. Results are compared at t=2.0. Figures 1 and 2 display the density profiles of different shock capturing methods on the baseline grid. It can be observed that the TVB limiter are able to suppress spurious oscillations effectively,while the artificial diffusivity schemes are better in terms of discontinuity resolution.
 |
| Fig. 1 Density profiles for Sod problem (second order scheme) |
 |
| Fig. 2 Density profiles for Sod problem (third order scheme) |
In order to further assess different methods,the variation of the computed L2 error (density) with CPU time is plotted in Fig. 3 on successively refined the grids. We have found out that with the second order scheme,the TVB limiter is able to achieve less numerical error with the same CPU time than artificial diffusivity schemes,while for the third order scheme,no significant evidence can be observed that the artificial diffusivity schemes are more accurate with higher order accuracy. Also,note that in Fig. 3 the slope of the ER scheme is smaller than the others. This is because the artificial diffusivity scheme depends more strongly on the empirical constant.
 |
| Fig. 3 Computed error (density) for Sod problem |
In the Shu-Osher problem,a Mach 3 shock interacts with a sinusoidal density wave,and the initial conditions are
The baseline grid is divided with 150 uniform elements,and the computational domain ranges from −5 to 5. Again we present the density profiles obtained with different methods in Figs. 4 and 5,and the variation of the computed error (density) with the CPU time in Fig. 6 through successively refining the grids.
 |
| Fig. 4 Density profiles for Shu-Osher problem (second order scheme) |
 |
| Fig. 5 Density profiles for Shu-Osher problem (third order scheme) |
 |
| Fig. 6 Computed error (density) for Shu-Osher problem |
With second order accuracy,BF causes the least dissipation to entropy waves,and with third order accuracy,the three artificial diffusivity schemes all perform much better than the TVB limiter. Similar to the last case,ER strongly depends on the user-specified constant. Also, note that the computed error with the TVB limiter is relatively large compared with that in the Sod problem,as the TVB limiter causes excessive dissipation to the entropy waves. 4.3 Double Mach problem
The double Mach problem is considered here to assess the feasibility of the shock capturing schemes for 2D cases. The domain ranges from 0 to 4 in x direction and from 0 to 1 in y direction. Initially a shock of Mach 10 is placed at x=1/6,y=0,making a 60◦ angle with the x-axis,and moves rightwards. For the bottom boundary,the inviscid wall condition is applied for 1/6≤ x ≤4,while for 0≤ x ≤ 1/6,the post-shock status is applied. For the top boundary, the conditions are given to agree with the Mach 10 shock movement. For the left boundary, inflow conditions are set,while for the right boundary,outflow conditions are set. Results are compared at t=0.2.
Three grids of 240×60,480×120,and 960×240 are employed. The results on the finest grids are presented here in Figs. 7−8. With second order accuracy,the TVB limiter is more dissipative while with third order accuracy,the artificial diffusivity methods are more accurate.
 |
| Fig. 7 Density contours for double Mach problem (960×240,second order scheme) |
 |
| Fig. 8 Density contours for double Mach problem (960×240,third order scheme) |
Table 1 displays the CPU cost when using different methods where it can be observed that TVB needs the least computational time as artificial diffusivity requires additional computations at each quadrature point. Among the artificial diffusivity schemes,BF is more efficient than the others. Also,note that the cost of the ER scheme increases significantly when the accuracy order increases from 2 to 3.
This problem is a transonic NACA0012 airfoil with the Mach number being 0.8 and the angle of attack being 1.25◦,and can be used to evaluate the various schemes with curvilinear grids and steady convergence ability. Figure 9 displays the enlarged portion of the computational grid,which places 99 points on the wall and 39 points normal to the wall.
 |
| Fig. 9 Close-up view of computational grid for transonic NACA0012 flow |
Density contours are displayed in Fig. 10 using different shock capturing schemes with third order accuracy. It can be seen that all schemes can resolve shocks well with no apparent spurious oscillations. To further exam the computational accuracy,the entropy production is plotted along wall surface in Figs. 11 and 12. It can be observed that TVB limiter causes much more entropy production than the others,which implies excessive numerical dissipation. Also,the entropy production decreases significantly with the order increasing for the artificial diffusivity schemes,among which BF is more dissipative.
 |
| Fig. 10 Density contours for transonic NACA0012 flow (third order scheme) |
 |
| Fig. 11 Entropy production along wall surface for transonic NACA0012 flow (second order scheme) |
 |
| Fig. 12 Entropy production along wall surface for transonic NACA0012 flow (third order scheme) |
In Fig. 13,the residual histories are demonstrated along the time,where it can be observed that TVB limiter is not able to achieve converged solutions. Also,the FR method is not able to obtain steady solution with third order accuracy as it cannot suppress the spurious oscillations well,and the BF method shows the best convergence performance in terms of efficiency.
 |
| Fig. 13 Convergence histories for transonic NACA0012 flow |
In this paper,systematic comparisons have been performed between four typical shock capturing schemes for the DG method,and they are chosen here to cover two well-known methodologies for shock capturing,i.e.,limiter and artificial diffusivity. Several typical shockdominated test cases are considered,and the following conclusions can be made:
(i) TVB limiter is able to suppress spurious oscillations better than the artificial diffusivity schemes,but tends to destroy the high order accuracy,especially for the flows with complex structures such as the Shu-Osher problem. On the contrary,the artificial diffusivity schemes can preserve small delicate structures much better with high order (higher than two) schemes.
(ii) According to the grid convergence test of the Sod problem,the ER scheme strongly depends on the user-specified constant than the others,and needs to adjust the constant for different grid resolutions.
(iii) The TVB limiter and the BF scheme are more efficient. The cost of the ER scheme increases significantly when the accuracy order goes to 3 from 2.
(iv) Among the three artificial diffusivity schemes,BF provides more numerical dissipation than the other two.
(v) For the steady problem,BF and ER are able to converge,while the TVB limiter and the FR scheme(third order accuracy) have failed to achieve convergence. Based on the above conclusions,we can make the following recommendations:
(I) For unsteady problems with just simplex discontinuities,the TVB limiter is suitable in terms of efficiency and robustness.
(II) For complex problems where shocks and small scale structures both exist,artificial diffusivity schemes can give more accurate results.
(III) For steady solutions,BF and ER should be chosen.
(IV) With the ER scheme,the user-specified constant may need to be adjusted for different grid resolution.
| [1] | Kroll, N. ADIGMA-A European Project on the Development of Adaptive Higher Order VariationalMethods for Aerospace Applications, ECCOMAS CDF, Egmond aan Zee, the Netherlands (2006) |
| [2] | Shu, C. W. TVB uniformly high-order schemes for conservation laws. Mathematics of Computation,49, 105-121 (1987) |
| [3] | Cockburn, B. and Shu, C. W. TVB Runge-Kutta local projection discontinuous Galerkin finiteelement method for conservation laws II: general framework. Mathematics of Computation, 52,411-435 (1989) |
| [4] | Biswas, R., Devine, K., and Flaherty, J. Parallel, adaptive finite element methods for conservationlaws. Applied Numerical Mathematics, 14, 255-283 (1994) |
| [5] | Burbeau, A., Sagaut, P., and Bruneau, C. H. A problem-independent limiter for high-order Runge-Kutta discontinuous Galerkin methods. Journal of Computational Physics, 169, 111-150 (2001) |
| [6] | Krivodonova, L. Limiters for high order discontinuous Galerkin methods. Journal of ComputationalPhysics, 226, 879-896 (2007) |
| [7] | Qiu, J. X. and Shu, C. W. Runge-Kutta discontinuous Galerkin method using WENO limiters.SIAM Journal of Scientific Computing, 26, 907-929 (2005) |
| [8] | Qiu, J. X., and Shu, C. W. Hermite WENO schemes and their application as limiters for Runge-Kutta discontinuous Galerkin method II: two dimensional case. Computers & Fluids, 34, 642-663(2005) |
| [9] | Luo, H., Baum, J. D., and Lohner, R. A Hermite WENO-based limiter for discontinuous Galerkinmethod on unstructured grids. Journal of Computational Physics, 225, 686-713 (2007) |
| [10] | Qiu, J. X. and Shu, C. W. A comparison of troubled-cell indicators for Runge-Kutta discontinuousGalerkin Methods using weighted essentially non-oscillatory limiters. SIAM Journal on ScientificComputing, 27, 995-1013 (2005) |
| [11] | Persson, P. O. and Peraire, J. Sub-cell shock capturing for discontinuous Galerkin methods. 44thAIAA Aerospace Sciences Meeting and Exhibit, American Institute of Aeronautics and Astronautics,Reno (2006) |
| [12] | Hartmann, R. Adaptive discontinuous Galerkin methods with shock capturing for the compressibleNavier-Stokes equations. International Journal for Numerical Methods in Fluids, 51, 1131-1156(2006)1374 Jian YU, Chao YAN, and Rui ZHAO |
| [13] | Xin, J. and Flaherty, J. E. Viscous stabilization of discontinuous Galerkin solutions of hyperbolicconservation laws. Applied Numerical Mathematics, 56, 444-458 (2006) |
| [14] | Bassi, F., Crivellini, A., Ghidoni, A., and Rebay, S. High order discontinuous Galerkin discretizationof transonic turbulent flows. 47th AIAA Aerospace Sciences Meeting Including the New HorizonsForum and Aerospace Exposition, American Institute of Aeronautics and Astronautics, Orlando(2009) |
| [15] | Barter, G. E. D. Shock capturing with PDE-based artificial viscosity for DGFEM, part I: formulation.Journal of Computational Physics, 229, 1810-1827 (2010) |
| [16] | Cockburn, B. and Shu, C. W. The Runge-Kutta discontinuous Galerkin method for conservationlaws V: multidimensional systems. Journal of Computational Physics, 141, 199-224 (1998) |
 2014, Vol. 35
2014, Vol. 35


























