Shanghai University
Article Information
- A. A. AFIFY, M. J. UDDIN, M. FERDOWS. 2014.
- Scaling group transformation for MHD boundary layer flow over permeable stretching sheet in presence of slip flow with Newtonian heating effects
- Appl. Math. Mech. -Engl. Ed., 35(11): 1375-1386
- http://dx.doi.org/10.1007/s10483-014-1873-7
Article History
- Received 2014-1-2;
- in final form 2014-5-12
2 American International University-Bangladesh, Dhaka 1213, Bangladesh;
3 Department of Mathematics, University of Dhaka, Dhaka 1000, Bangladesh
The investigation of flow and heat transfer over a surface which moves continuously has received considerable interest of researchers due to its diverse engineering applications,such as polymer industry,cooling of metallic sheets or electronic chips,crystal growing,stretching of plastic films,and materials manufactured by extrusion. Sakiadis[1,2,3] became the first person to investigate the boundary layer flow past a surface which moves with a constant speed. Crane[4] studied the dynamics of the flow over a stretching surface. Accordingly,numerous researchers[5,6,7,8,9,10,11,12,13,14,15,16,17,18] have investigated various aspects of this model for both regular and nanofluid over linearly and nonlinearly stretching and shrinking surfaces.
In 1994,Merkin[19] became the first person to create the term Newtonian heating for describing the characteristic of heat transfer problems. Following him,many researchers[20,21,22,23] have examined Newtonian heating effects over various geometry placed in a porous and clear medium. Very recently,Salleh et al.[24,25,26,27,28] and Merkin et al.[29] investigated the effects of Newtonian heating on the boundary layer flow and heat transfer past different geometry surfaces.
According to Chaundary and Jain[30,31],Merkin’s model[19] is applicable in diverse engineering applications,such as high performance building insulation,heat exchangers,thermal energy conversion,and solar collectors. In all of the above mentioned studies,the effect of slip flow is negligible. However,the effects of slip flow and Newtonian heating are very important in heat transfer problems. Beavers and Joseph[32] discussed the effect of slip flow past a permeable surface. Recently,many investigators[33,34,35,36,37] have analyzed the phenomenon of wall-slip fluid.
Symmetries of the differential equations are calculated using Lie symmetry group. For details of the method,see Refs. [38,39,40]. Recently,numerous researchers[41,42,43,44,45,46,47,48],have used Lie symmetry group to discuss the similarity solution for the differential equations. In the light of this,the main aim of our study is to find group invariant solutions of magnetohydrodynamic (MHD) boundary layer flow towards a porous moving plate using the Lie symmetry group and to investigate the effects of slip flow,Newtonian heating,and thermal radiation. Numerical results and discussions are presented through graphs and tables. 2 Formulation of problem
Two dimensional steady,boundary layer flow and heat transfer of a viscous,incompressible and electrically conducting fluid towards a porous moving surface with Newtonian heating and radiation effects is considered. Two equal but opposite forces are applied along the x-axis so that the surface is stretched with a speed proportional to the distance from the origin. The coordinate system and flow configuration is shown in Fig. 1. The assumptions we made are as follows:
 |
| Fig. 1 Physical model coordinate system |
(i) We define the temperature at the surface as Tw( ) and the ambient temperature as T∞.
) and the ambient temperature as T∞.
(ii) The external electric field,the induced magnetic field,Joule heating,and viscous dissipation effects are neglected.
(iii) The stretching sheet is obeyed to the slip-flow condition and Merkin model[19].
(iv) All physical quantities are constant except the electric conductivity.
Under these assumptions,the governing boundary layer equations can be written as
The relevant boundary conditions are listed as follows: The Rosseland approximation[49] is used to define the radiative heat flux term qr as where σ1 and K1 are the Stefan-Boltzmann constant and the mean absorption coefficient. It is assumed that a temperature difference inside the boundary layer is sufficiently small so that T4 can write as a linear function of the temperature. Expanding the T4 in Taylor series about T∞ and discarding higher order terms,we obtain Substituting (5) and (6) into (3),we get where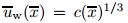 is the velocity of the moving plate,
is the velocity of the moving plate,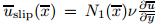 is the slip
velocity,with N1(x) being the velocity slip factor,hs(x) is the heat transfer coefficient,u and v
are the velocity components along axes,ρ is the density of the fluid,ν is the kinematic viscosity,
c is constant,σ = σ0u is the electric conductivity,cp is the specific heat at constant pressure,α
is the thermal diffusivity,and vw is the mass transfer velocity. Following Helmy[50],a magnetic
field of variable strength
is the slip
velocity,with N1(x) being the velocity slip factor,hs(x) is the heat transfer coefficient,u and v
are the velocity components along axes,ρ is the density of the fluid,ν is the kinematic viscosity,
c is constant,σ = σ0u is the electric conductivity,cp is the specific heat at constant pressure,α
is the thermal diffusivity,and vw is the mass transfer velocity. Following Helmy[50],a magnetic
field of variable strength 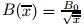 is applied in the perpendicular direction of the plate.
2.1 Lie symmetry analysis
is applied in the perpendicular direction of the plate.
2.1 Lie symmetry analysis
The following dimensionless variables are introduced:
Also introduce the stream function ψ defined as
which satisfies (1),and (2) and (7) are transformed to
The boundary conditions (4) take the following form:
along with θ(0) = 1 (CWT).Here,M = σ0B02/ρ is the magnetic parameter,R = 3N/(3N +4) is the radiation parameter with N = kK1/(4σ1T∞3 ). Also,Pr = μcp/k is Prandtl number.
We introduce the simplified form of one-parameter transformation group[51,52],
Here,ε is the parameter of the group and αi (i = 1,2,· · · ,7) are arbitrary real numbers.(13) is regarded as a point transformation transforming the coordinates (x,y,ψ,θ,N1,vw,hs) to (x*,y*,ψ*,θ*,N1*,vw*,hs*). The relationship among the exponents αi (i = 1,2,· · · ,7) such that
are sought.(10) and (11) are invariant under the group of transformation Γ[38]. By (13),(10) and (11) become
The system remains invariant under the group transformation Γ,the following relations among the parameters are deduced:
The boundary conditions will be invariant under Γ if
Solving (17) and (18) gives
With these relationships,the set of transformations Γ reduces to
Expanding (20) by Taylor’s series in powers of ε and keeping terms up to the order ε,we obtain the following characteristic equations:
2.2 Similarity equationsSolving the above characteristic equations,we obtain
Here,(N1)0,(hs)0,and (vw)0 are the constant momentum slip factor,the heat transfer coefficient, and the mass transfer velocity,respectively.Substitution of (22) into (10)-(11) leads to the following similarity equations:
with the boundary conditions along with θ(0) = 1 (CWT).Here,a = ν(N1)0/L is the velocity slip parameter,γ = L(hs)0 is the conjugate parameter for Newtonian heating,fw = −3L(vw)0/2ν is the suction/injection parameter with fw > 0 for suction,fw < 0 for injection and fw = 0 for nonporous plate whereas vw0 is the velocity of suction if vw0 < 0 and injection if vw0 > 0. We note that γ = 0 implies a plate which is insulated and γ → ∞ refers to isothermal plate. The sheet surface temperature,the local skin friction factor and the local heat transfer rates can easily be determined in terms of θ(0),f''(0),−θ'(0), respectively. 3 Numerical solutions
The transformed (23) and (24) with boundary conditions (25) are solved numerically by using an efficient Runge-Kutta-Fehlberg fourth-fifth order numerical method under Maple 13. The accuracy of the method has been tested with different papers (White and Subramanian[54], and Uddin et al.[55]). We replaced the far filed boundary conditions (25) by a finite value of 30 for similarity variable ηmax as follows:
The choice of ηmax = 30 ensures that all numerical solutions satisfies the far field asymptotic values in a correct manner. The range of parameters values we have used during numerical computations are 0 ≤ M ≤ 2,0.5 ≤ γ ≤ 2,0 ≤ a ≤ 2,−0.5 ≤ fw ≤ 0.5,0 ≤ N < ∞, 0.72 ≤ Pr ≤ 2. 4 Results and discussion(23) and (24) subject to the boundary conditions (25) have been solved numerically for various values of the parameters a,γ,M,N,and fw. To test the validity of the numerical method,we have compared our shear stress represented by f''(0) for M = a = γ = 0 and selected values of fw with Cortell[53]. The comparison is shown in Table 1,and an excellent agreement is obtained. In Table 2,comparison of θ'(0) for several values of N in the case of an impermeable surface (CWT) with available results of Cortell[53],are made and found in excellent agreement. Moreover,comparison of θ'(0) for several values of fw,N,and Pr=2 with available results of Cortell[53],are made (see Table 3) and found in excellent agreement. Finally,the numerical values for different controlling parameters are tabulated in Table 4. It is observed from Table 4 that the shear stress and the rate of heat transfer decrease with an increase in slip parameter. This is because the heat flow is transferred from the surface to the fluid further away from the surface. It is seen that the rate of heat transfer decreases with an increase in slip parameter. On the other hand,the shear stress decreases and approaches zero with an increase in slip parameter. In addition,it is observed that the rate of heat transfer increases with an increase in radiation and conjugate parameters. This is because increasing N and γ leads to increase the heat transfer rate from the surface,which raises the temperature of the fluid. It is also observed that the shear stress increases with an increase in magnetic parameter,and the reverse effect is noticed for the rate of heat transfer. Physically,this is because the presence of the magnetic field leads to decelerate the velocity,which increases the velocity gradient at the stretching sheet. Figures 2-10 are drawn in order to see the influence of radiation parameter,Prandtl number,slip parameter,conjugate parameter,and suction/injection parameter on the velocity and temperature distributions for both cases of the presence magnetic parameter (M ≠ 0) and in the absence magnetic parameter (M = 0), respectively. Figures 2 and 3 depict the effects of slip parameter a,and suction/injection fw,on the dimensionless stream function. It is noticed from these figures that the stream function decreases as slip parameter increases for both cases. Also,the imposition of surface suction (fw > 0) leads to decrease the stream function whereas the opposite results hold with imposition of surface injection (fw < 0) for both cases. The effects of slip parameter a,on the dimensionless velocity and temperature distributions are shown in Figs. 4 and 5. Note that the velocity decreases,near the surface whereas the opposite results show far away from the surface, as slip parameter increases for both cases. This is because the presence of slip parameter leads to decelerate the flow velocity near the stretching sheet. In addition,the fluid temperature and the thermal boundary layer decrease by increasing slip parameter a,for both cases. Figures 6 and 7 show the effects of suction/ injection parameter fw on the velocity and temperature distributions for both cases. For the injection case (fw < 0),the velocity distribution decreases whereas the opposite results hold with the suction case (fw > 0). The thermal boundary layer thickness and temperature distribution decrease with the case of suction (fw > 0). However, the opposite trend is true with the case of injection (fw < 0).
 |
 |
 |
 |
| Fig. 2 Effect of a and M on stream function distribution |
 |
| Fig. 3 Effect of fw and M on stream function distribution |
 |
| Fig. 4 Effect of a and M on velocity distribution |
 |
| Fig. 5 Effect of a and M on temperature distribution |
 |
| Fig. 6 Effect of fw and M on velocity distribution |
 |
| Fig. 7 Effect of fw and M on temperature distribution |
 |
| Fig. 8 Effect of γ and M on temperature distribution |
 |
| Fig. 9 Effect of N andM on temperature distribution |
 |
| Fig. 10 Effect of Pr and M on temperature distribution |
Figures 8-10 show the effects of conjugate parameter γ,radiation parameter N,and Prandtl number Pr on the dimensionless temperature distribution. It is seen that the temperature distribution increases as conjugate parameter increases for both cases (see Fig. 8). It is also seen that the temperature distribution increases with an increase in radiation parameter for both cases (see Fig. 9). This is because the thermal boundary layer thickness and the radiative heat flux increase with an increase in radiation parameter. From Fig. 10,it is observed that the temperature distribution and the thermal boundary layer thickness decrease with an increase in Prandtl number for the case (M = 0). In addition,the opposite results occur for the other case (M ≠ 0). Physically,the presence of a magnetic field generates a resistive-type magnetic force which decreases the velocity of the fluid while it increases both the thermal boundary layer thickness and temperature of the fluid. 5 Conclusions
In the present paper,Lie symmetry method is used to find the similarity solutions of MHD boundary layer flow over a moving permeable stretching sheet with slip flow,Newtonian heating, and thermal radiation effects. The numerical results indicate that the combined effects of magnetic field,slip flow,and Newtonian heating all have a significant impact in controlling the shear stress and the rate of heat transfer in heat transfer problems. The main findings are as follows.
(i) Both velocity and temperature distributions change with an increase in a magnetic parameter.
(ii) The shear stress increases while the rate of heat transfer decreases with magnetic parameter.
(iii) The shear stress and the rate of heat transfer decrease as slip parameter increases.
(iv) The rate of heat transfer and the temperature distribution increase with radiation and conjugate parameters.
(v) Increasing Prandtl number (M = 0),leads to decrease the temperature distribution, while the opposite results hold for the case (M ≠ 0).
| [1] | Sakiadis, B. C. Boundary-layer behavior on continuous solid surfaces, part I: boundary-layerequations for two-dimensional and axisymmetric flow. AIChE Journal, 7, 26-28 (1961) |
| [2] | Sakiadis, B. C. Boundary-layer behavior on continuous solid surfaces, part II: the boundary-layeron a continuous flat surface. AIChE Journal, 7, 221-225 (1961) |
| [3] | Sakiadis, B. C. Boundary-layer behavior on continuous solid surfaces, part III: the boundary-layeron a continuous cylindrical surface. AIChE Journal, 7, 467-472 (1961) |
| [4] | Crane, L. J. Flow past a stretching plate. Zeitschrift für angewandte Mathematik und Physik, 21,645-647 (1970) |
| [5] | Chakrabarti, A. and Gupta, A. S. Hydromagnetic flow and heat transfer over a stretching sheet.Quarterly of Applied Mathematics, 37, 73-78 (1977) |
| [6] | Andersson, H. I. MHD flow of a viscous fluid past a stretching surface. Acta Mechanica, 95,227-230 (1992) |
| [7] | Chiam, T. C. Magnetohydrodynamic boundary layer flow due to a continuously moving flat plate.Computers & Mathematics with Applications, 26, 1-7 (1993) |
| [8] | Vajravelu, K. and Hadjinicolaou, A. Convective heat transfer in an electrically conducting fluidat a stretching surface with uniform free stream. International Journal of Engineering Science,35, 1237-1244 (1997) |
| [9] | Pop, I. and Na, T. Y. A note on MHD flow over a stretching permeable surface. MechanicsResearch Communications, 25, 263-269 (1998) |
| [10] | Kumari, M. and Nath, G. Flow and heat transfer in a stagnation point flow over a stretchingsheet with a magnetic field. Mechanics Research Communications, 26, 469-478 (1999) |
| [11] | Sajid, M. and Hayat, T. Influence of thermal radiation on the boundary layer flow due to exponentiallystretching sheet. International Communications in Heat and Mass Transfer, 35, 347-356(2008) |
| [12] | Abo-Eldahab, E. M. and El Aziz, M. A. Blowing/suction effect on hydromagnetic heat transferby mixed convection from an inclined continuously stretching surface with internal heat generation/absorption. International Journal of Thermal Sciences, 43, 709-719 (2004) |
| [13] | Sahoo, B. Flow and heat transfer of a non-Newtonian fluid past a stretching sheet with partialslip. Communications in Nonlinear Science and Numerical Simulation, 15, 602-615 (2010) |
| [14] | Datti, P. S., Prasad, K. V., Abel, M. S., and Joshi, A. MHD viscoelastic fluid flow over a nonisothermalstretching sheet. International Journal of Engineering Science, 42, 935-946 (2004) |
| [15] | Elbashbeshy, E. M. A. Heat transfer over a stretching surface with variable surface heat flux.Journal of Physics D: Applied Physics, 31, 1951-1954 (1998) |
| [16] | Seddeek, M. A. Heat and mass transfer on a stretching sheet with a magnetic field in a visco-elasticfluid flow through a porous medium with heat source or sink. Computational Materials Science,38, 781-787 (2007) |
| [17] | Shit, G. C. and Haldar, R. Effects of thermal radiation on MHD viscous fluid flow and heattransfer over nonlinear shrinking porous sheet. Appl. Math. Mech. -Engl. Ed., 32, 677-688 (2011)DOI 10.1007/s10483-011-1448-6 |
| [18] | Vajravelu, K., Prasad, K. V., Sujatha A., and Ng, C. O. MHD flow and mass transfer of chemicallyreactive upper convected Maxwell fluid past porous surface. Appl. Math. Mech. -Engl. Ed., 33,899-910 (2012) DOI 10.1007/s10483-012-1593-8 |
| [19] | Merkin, J. H. Natural convection boundary-layer flow on a vertical surface with Newtonian heating.International Journal of Heat and Fluid Flow, 15, 392-398 (1994) |
| [20] | Lesnic, D., Ingham, D. B., and Pop, I. Free convection boundary layer flow along a vertical surfacein a porous medium with Newtonian heating. International Journal of Heat and Mass Transfer,42, 2621-2627 (1999) |
| [21] | Lesnic, D., Ingham, D. B., and Pop, I. Free convection from a horizontal surface in a porousmedium with Newtonian heating. Journal of Porous Media, 3, 227-235 (2000) |
| [22] | Lesnic, D., Ingham, D. B., Pop, I., and Storr, C. Free convection boundary layer flow above anearly horizontal surface in a porous medium with Newtonian heating. Heat and Mass Transfer,40, 665-672 (2004) |
| [23] | Pop, I., Lesnic, D., and Ingham, D. B. Asymptotic solutions for the free convection boundarylayerflow along a vertical surface in a porous medium with Newtonian heating. Hybrid Methodsin Engineering, 2, 31-40 (2000) |
| [24] | Salleh, M. Z., Nazar, R., and Pop, I. Forced convection boundary layer flow at a forward stagnationpoint with Newtonian heating. Chemical Engineering Communications, 196, 987-996 (2009) |
| [25] | Salleh, M. Z., Nazar, R., and Pop, I. Mixed convection boundary layer flow about a solid spherewith Newtonian heating. Archives of Mechanics, 62, 283-303 (2010) |
| [26] | Salleh, M. Z., Nazar, R., and Pop, I. Modeling of free convection boundary layer flow on a spherewith Newtonian heating. Acta Applicandae Mathematicae, 112, 263-274 (2010) |
| [27] | Salleh, M. Z., Nazar, R., and Pop, I. Modelling of boundary layer flow and heat transfer over astretching sheet with Newtonian heating. Journal of the Taiwan Institute of Chemical Engineers,41, 651-655 (2010) |
| [28] | Salleh, M. Z., Nazar, R., Arifin, N. M., Merkin, J. H., and Pop, I. Forced convection heat transferover a horizontal circular cylinder with Newtonian heating. Journal of Engineering Mathematics,69, 101-110 (2011) |
| [29] | Merkin, J. H., Nazar, R., and Pop, I. The development of forced convection heat transfer neara forward stagnation point with Newtonian heating. Journal of Engineering Mathematics, 74,53-60 (2012) |
| [30] | Chaundary, R. C. and Preeti, J. Unsteady free convection boundary-layer flow past an impulsivelystarted vertical surface with Newtonian heating. Romanian Journal of Physics, 51, 911-925 (2006) |
| [31] | Chaundary, R. C. and Preeti, J. An exact solution to the unsteady free convection boundary layerflow past an impulsively started vertical surface with Newtonian heating. Journal of EngineeringPhysics and Thermophysics, 80, 954-960 (2007) |
| [32] | Beavers, G. S. and Joseph, D. D. Boundary conditions at a naturally permeable wall. Journal ofFluid Mechanics, 30, 197-207 (1967) |
| [33] | Ariel, P. D. Two dimensional stagnation point flow of an elastico-viscous fluid with partial slip.Zeitschrift für angewandte Mathematik und Mechanik, 88, 320-324 (2008) |
| [34] | Fang, T., Zhang, J., and Yao, S. Slip MHD viscous flow over a stretching sheet--an exact solution.Communications in Nonlinear Science and Numerical Simulation, 14, 3731-3737 (2009) |
| [35] | Aman, F., Ishak, A., and Pop, I. Mixed convection boundary layer flow near stagnationpointon vertical surface with slip. Appl. Math. Mech. -Engl. Ed., 32, 1599-1606 (2011) DOI10.1007/s10483-011-1526-x |
| [36] | Yazdi, M. H., Abdullah, S., Hashim, I., and Sopian, K. Slip MHD liquid flow and heat transferover non-linear permeable stretching surface with chemical reaction. International Journal of Heatand Mass transfer, 54, 3214-3225 (2011) |
| [37] | Bhattacharyya, K., Mukhopadhyay, S., and Layek, G. C. Slip effects on boundary layer stagnationpointflow and heat transfer towards a shrinking sheet. International Journal of Heat and MassTransfer, 54, 308-313 (2011) |
| [38] | Hansen, A.G. Similarity Analysis of Boundary Layer Problems in Engineering, Prentice Hall,Englewood Cliffs, U. S.A. (1964) |
| [39] | Olver, P. J. Application of Lie Groups to Differential Equations, Springer-Verlag, New York (1986) |
| [40] | Bluman, G. W. and Kumei, S. Symmetries and Differential Equations, Springer, New York (1989) |
| [41] | Fan, J. R., Shi, J. M., and Xu, X. Z. Similarity solution of free convective boundary-layer behaviorat a stretching surface. Heat and Mass Transfer, 35, 191-196 (1999) |
| [42] | Afify, A. A. Some new exact solutions for MHD aligned creeping flow and heat transfer in secondgrade fluids by using Lie group analysis. Nonlinear Analysis-Theory Methods & Applications, 70,3298-3306 (2009) |
| [43] | Abdul-Kahar, R., Kandasamy, R., and Muhaimin, I. Scaling group transformation for boundarylayer flow of a nanofluid past a porous vertical stretching surface in the presence of chemicalreaction with heat radiation. Computers and Fluids, 52, 15-21 (2011) |
| [44] | Afify, A. A. and Elgazery, N. S. Lie group analysis for the effects of chemical reaction on MHDstagnation-point flow of heat and mass transfer towards a heated porous stretching sheet withsuction or injection. Nonlinear Analysis: Modelling and Control, 17, 1-15 (2012) |
| [45] | Hamad, M. A. A. and Ferdows, M. Similarity solution of boundary layer stagnation-point flow towardsa heated porous stretching sheet saturated with a nanofluid with heat absorption/generationand suction/blowing: a Lie group analysis. Communication in Nonlinear Science and NumericalSimulation, 17, 132-140 (2012) |
| [46] | Rosmila, A. B., Kandasamy, R., and Muhaimin, I. Lie symmetry group transformation for MHDnatural convection flow of nanofluid over linearly porous stretching sheet in presence of thermalstratification. Appl. Math. Mech. -Engl. Ed., 33, 593-604 (2012) DOI 10.1007/s10483-012-1573-9 |
| [47] | Uddin, M. J., Khan, W. A., and Ismail, A. I. M. Free convection boundary layer flow from aheated upward facing horizontal flat plate embedded in a porous medium filled by a nanofluidwith convective boundary condition. Transport in Porous Media, 92, 867-881 (2012) |
| [48] | Ferdows, M., Uddin, M. J., and Afify, A. A. Scaling group transformation for MHD boundarylayer free convective heat and mass transfer flow past a convectively heated nonlinear radiatingstretching sheet. International Journal of Heat and Mass Transfer, 56, 181-187 (2013) |
| [49] | Sparrow, E. M. and Cess, R. D. Radiation Heat Transfer, Hemisphere, Washington, D. C. (1978) |
| [50] | Helmy, K. A. MHD boundary layer equations for a power-law fluid with variable electric conductivity.Meccanica, 30, 187-200 (1995) |
| [51] | Tapanidis, T., Tsagas, G., and Mazumdar, H. P. Application of scaling group of transformationsto viscoelastic second grade fluid flow. Nonlinear Functional Analysis and Applications, 8, 345-350(2003) |
| [52] | Mukhopadhyay, S. and Layek, G. C. Effects of variable fluid viscosity on flow past a heatedstretching sheet embedded in a porous medium in presence of heat source/sink. Meccanica, 47,863-876 (2012) |
| [53] | Cortell, R. Heat and fluid flow due to non-linearly stretching surfaces. Applied Mathematics andComputation, 217, 7564-7572 (2011) |
| [54] | White, R. E. and Subramanian, V. R. Computational Methods in Chemical Engineering withMaple, Springer, New York (2010) |
| [55] | Uddin, M. J., Yusoff, N. H. M., Bég, O. A., and Ismail, A. I. M. Lie group analysis and numericalsolutions of boundary layer flow of non-Newtonian nanofluids along a horizontal plate in porousmedium with internal heat generation. Physica Scripta, 87, 025401 (2013) |
 2014, Vol. 35
2014, Vol. 35
























