Shanghai University
Article Information
- S. MANSUR, A. ISHAK, I.POP. 2014.
- Flow and heat transfer of nanofluid past stretching/shrinking sheet with partial slip boundary conditions
- Appl. Math. Mech. -Engl. Ed., 35(11): 1401-1410
- http://dx.doi.org/10.1007/s10483-014-1878-7
Article History
- Received 2014-1-22;
- in final form 2014-5-29
2. Centre of Modelling and Data Analysis, School of Mathematical Sciences, Faculty of Science and Technology, Universiti Kebangsaan Malaysia, Selangor 43600, Malaysia;
3. Department of Mathematics, Babeş-Bolyai University, Cluj-Napoca 400084, Romania
Nanofluid is a term coined by Choi[1] ,referring to dispersions of nanoparticles in the base fluids such as water,ethylene glycol,and propylene glycol. The capability of a nanofluid to enhance thermal conductivity was first reported by Masuda et al. [2] .Choi[1] discovered that the addition of less than 1% of nanoparticles into the base fluid doubles the heat conductivity of the fluid. Other characteristics of nanofluid include less clogging of tube and the stability for long term as compared with micro- and millimeter sized particles [2,3,4,5,6] . Buongiorno [7] developed an explanation for the abnormal convective heat transfer enhancement in nanofluids. In his paper,it is identified that Brownian diffusion and thermophoresis are the two most important nanoparticle/base-fluid slip mechanisms. Nield and Kuznetsov [8,9] and Kuznetsov and Nield[10,11] were among the firsts to employ the Buongiorno model in their studies. They identified that the similarity solutions depend on the four dimensionless parameters,namely,Lewis numberLe,buoyancy-ratio parameter Nr,Brownian motion parameter Nb,and thermophoresis parameter Nt. Khan and Pop [12] used the model of Nield and Kuznetsov [9] to study the boundary layer flow of a nanofluid past a stretching sheet with a constant surface temperature. On the other hand,Makinde and Aziz[13] performed a similar study with a convective surface boundary condition.
The study of boundary layer flow due to a stretching sheet has garnered considerable interests [14,15,16,17,18,19] . Flow of a boundary layer over a stretching sheet is important in applications, such as extrusion,wire drawing,metal spinning,and hot rolling [14] . The pioneering study of stretching sheet by Crane [15] showed an exact analytical solution for the steady two-dimensional stretching of a surface in a quiescent fluid. His study has then become the benchmark for other researchers. Crane’s study was extended by Wang [16] to include both suction and slip where he found the solution and proved the uniqueness of the said solution for both two-dimensional stretching and axisymmetric stretching. On the other hand,the study on boundary layer flow due to a shrinking sheet has also attracted much attention. Miklavˇciˇ c and Wang [20] pioneered the study of flow on a shrinking sheet. They found that the vorticity over the shrinking sheet is not confined within a boundary layer. To confine the velocity of the shrinking sheet in the boundary layer,Miklavˇ ciˇ c and Wang [20] imposed an adequate suction on the boundary while Wang [21] considered a stagnation flow. Ever since,numerous studies emerge,investigating different aspects of this problem. Fang et al. [22] solved the viscous flow over a shrinking sheet analytically using a second order slip flow model. They found that the solution has two branches,or dual solutions,in a certain range of the parameters. Bhattacharyya et al. [23] observed that the velocity and thermal boundary layer thicknesses for the second solutions are always larger than those of the first solutions. Weidman et al. [24] ,Postelnicu and Pop [25] ,and Ro¸sca and Pop [26] performed a stability analysis to show that the upper branch solutions are stable and physically realizable while the lower branch solutions are not stable,and therefore, not physically possible.
During the recent years,it has been found that rarefied gas flows with slip boundary conditions are often encountered in the micro-scale devices and low-pressure situations [27] .The effects of slip conditions are also very important in technological applications such as in the polishing of artificial heart valves and the internal cavities. Many studies were conducted to include slip condition. Wang [28] reported that the partial slip between the fluid and the moving surface may occur in situations that the fluid is particulate such as emulsions,suspensions, foams,and polymers. Noghrehabadi et al. [29] showed that the slip parameter greatly influences the flow velocity,the surface shear stress,the local Nusselt number,and the local Sherwood number. Sharma et al. [30] found that the surface heat transfer of a nanofluid increases with the increasing velocity slip. Aman et al. [31] reported that while the velocity slip increases the surface heat transfer,the thermal slip reduces the heat transfer rate at the surface.
In the present paper,we study the boundary layer flow and heat transfer characteristics of a nanofluid past a permeable stretching/shrinking sheet with hydrodynamic and thermal slip boundary conditions. The paper is,in fact,an extension of Noghrehabadi et al. [29] to the case of a permeable shrinking sheet,which was not considered previously. Furthermore,we also impose adequate suction at the boundary that is necessary to confine the vorticity in the boundary layer. A closed form analytical solution has also been obtained when the velocity slip is absent. The dependency of the local Nusselt number and the local Sherwood number on five parameters,namely,the stretching/shrinking,velocity slip,thermal slip,Brownian motion, and thermophoresis parameters is the main focus of the investigation. Numerical solutions are presented graphically and in tabular form to show the effects of these parameters on the above mentioned quantities. It is worth pointing out to this end that in many industrial applications, such as power,manufacturing,and transportation,nanofluids are commonly used for cooling any sort of high energy device. However,these fluids have limited heat transfer capabilities due to their low heat transfer properties. Thus,effective cooling techniques are greatly needed. The characteristic feature of nanofluids is thermal conductivity enhancement,a phenomenon observed by Masuda et al. [2] . This phenomenon suggests the possibility of using nanofluids in advanced nuclear systems (Buongiorno and Hu[32] ). Buongiorno [7] presented a comprehensive survey of convective transport in nanofluids,who says that a satisfactory explanation for the abnormal increase of the thermal conductivity and viscosity is yet to be found. He focused on the further heat transfer enhancement observed in convective situations. 2 Mathematical formulation
Consider a steady,two-dimensional flow of a viscous and incompressible fluid with hydrodynamic and thermal slip boundary conditions in the region y>0 driven by a permeable stretching/shrinking surface located at y= 0 in a nanofluid as shown in Fig. 1,where thexand yaxes are measured along and normal to the surface of the sheet,respectively. It is assumed that the stretching/shrinking velocity is Uw(x)=cx,where c>0 and c<0 correspond to stretching and shrinking sheets,respectively. It is also assumed that the uniform temperature and the uniform nanofluid volume fraction at the surface of the sheet are Tw and Cw,while the uniform temperature and the uniform nanofluid volume fraction far from the surface of the sheet (inviscid fluid) are T∞ and C∞,respectively. Further,it is assumed that the constant mass flux velocity is v0 with v0<0 for suctionandv0>0 for injection or withdrawal of the fluid. Under these assumptions,the governing equations for the steady conservation of momentum, thermal energy,and nanoparticle volume fraction equations can be written as (Buongiorno [7] and Noghrehabadi [29] )
whereuandvare the velocity components along thex-andy-axes,respectively,pis the fluid pressure,Tis the fluid temperature,Cis the nanoparticle volume fraction,αis the thermal diffusivity of the fluid,ν is the kinematic viscosity,DBis the Brownian diffusion coefficient,andDTis the thermophoresis diffusion coefficient. Moreover,τ =(ρC)p/(ρC)f is the ratio between the effective heat capacity of the nanoparticle material and heat capacity of the fluid with ρf and ρp being the density of the fluid and of the particles,respectively. In this paper,we employ the model proposed by Buongiorno [7] ,which paid attention to the effect of Brownian motion and thermophoresis on the flow and heat transfer of a nanofluid. The present model is subjected to the following boundary conditions [33] : whereLdenotes the slip length [29] ,His a proportionality constant,and σis the constant stretching/shrinking parameter with σ>0 for stretching and σ<0 for shrinking. The governing equations (1)−(5) subjected to the boundary conditions (6) can be expressed in a simpler form by introducing the following similarity transformations [29,34] : whereηis the similarity variable,and ψ is the stream function defined as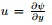 and v=
and v=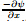 ,which identically satisfies (1). By employing the boundary layer approximations and the
similarity variables (7),(2)−(5) reduce to the following ordinary differential equations:
and the boundary conditions (6) and (7) become
where primes denote differentiation with respect toη.Further,Pris the Prandtl number,Leis
the Lewis number,sis the mass flux parameter with s >0 forsuctionand s<0 for injection,
respectively,Nb is the Brownian motion parameter,Ntis the thermophoresis parameter, λis
the velocity slip parameter,and ξ is the thermal slip parameter,which are defined as
We notice as in Ref. [10] that when Nb and Ntare zero,(8) and (9) involve just two
dependent variables,namely f(η) and θ(η),and the boundary-value problem for these two
variables reduces to the classical problem solved by Crane
[15]
and Wang
[16]
(the boundaryvalue problem for φ(η) then becomes ill-posed and is of no physical significance).
,which identically satisfies (1). By employing the boundary layer approximations and the
similarity variables (7),(2)−(5) reduce to the following ordinary differential equations:
and the boundary conditions (6) and (7) become
where primes denote differentiation with respect toη.Further,Pris the Prandtl number,Leis
the Lewis number,sis the mass flux parameter with s >0 forsuctionand s<0 for injection,
respectively,Nb is the Brownian motion parameter,Ntis the thermophoresis parameter, λis
the velocity slip parameter,and ξ is the thermal slip parameter,which are defined as
We notice as in Ref. [10] that when Nb and Ntare zero,(8) and (9) involve just two
dependent variables,namely f(η) and θ(η),and the boundary-value problem for these two
variables reduces to the classical problem solved by Crane
[15]
and Wang
[16]
(the boundaryvalue problem for φ(η) then becomes ill-posed and is of no physical significance).
 |
| Fig. 1 Geometry of problem for stretching and shrinking sheets |
The physical quantities of interest are the skin friction coefficient Cf,the local Nusselt numberNuxand the local Sherwood number Shx,which are given by
where τw,qw,and qm are the surface shear stress,the surface heat flux,and the surface mass flux,respectively. Using similarity variables (7),we obtain Cf Rex where Rex=Uwx/ν is the local Reynolds number.It is worth mentioning that for σ=−1 (shrinking sheet),(8) with the associated boundary conditions (11) becomes identical with (7) subjected to boundary conditions (8) from the papers by Fang and Zhang [35] ,and Fang et al. [22] for the case of first order slip. In fact,for λ=0and ξ= 0 (no slip condition),the boundary value problems (8)−(11) have the following closed form analytical solution:
where γ(>0) is given by the quadratic equation with the solution Thus,we have Hence,we can compare the numerical results for f'' (0) with the analytical ones given by (18). 3 Results and discussionThe set of ordinary differential equations (8)-(10) subjected to boundary conditions (11) are solved numerically using a shooting method. In this method,the dual solutions are obtained by setting different initial guesses for the values of f'' (0),θ' (0),and φ' (0). The asymptotic boundary conditions (11) at η=∞ are replaced by η=15,which is sufficient for all the velocity, temperature,and concentration profiles to vanish asymptotically. Throughout the paper,we have fixed Prandtl numberPrto be equal to 6.8,which is appropriate for a water-base nanofluid. Furthermore,suction parametersis taken in the range s>2 due to the fact that the solutions for a shrinking sheet may only exist if adequate suction is imposed [21] . In choosing the values of Brownian motion parameterNb,thermophoresis parameter Nt,Lewis number Le,we adhere to Buongiorno [7] who stated that Le≥ and Le·Nbt≥1,whereNbt is the ratio between the Brownian diffusivity coefficient and thermophoresis coefficient for particles with diameters of 1nm−100 nm. Furthermore,Noghrehabadi et al. [29] studied Nb and Nt in the range 0.1-0.5 andLein the range 1-25. In the present study,we consider Nbin the range 0.3-0.5 and Nt in the range 0.1-0.5 where Leis fixed at 2. These values are found to satisfy the rules laid out by Buongiorno [7] . Other values of parameters such as the velocity slip and thermal slip are arbitrarily selected and may represent the general trend. Numerical results for f'' (0) are compared with analytical results obtained from (18) and are shown in Table 1,where they are found to be in excellent agreement,cementing the validity of the present numerical results.
Tables 2 and 3 and Figs. 2-5 show the variations of the local Nusselt number NuxRex-1/2 (representing the heat transfer rate at the surface) and the local Sherwood number ShxRex-1/2 (representing the mass transfer rate at the surface) with σ for different values of the velocity slip parameter λ,thermal slip parameter ξ,Brownian motion parameter Nb,and thermophoresis parameterNt. As can be seen,there are more than one solution obtained for a fixed value of σ.When σ is equal to a certain value σ= σc,where σc (<0) is the critical value of σ,there is only one solution,and when σ< σc,mputations have been performed until the point where the solution does not converge. The critical values σc are shown in the figures. Based on our computations,we found that σc=2.250 0,2.598 4,and 3.149 3 for λ=0,0.1,and 0.25 respectively. Although only the first solution is stable and physically realizable [24,25,26] ,the second solution is of mathematical interest as the differential equations are concerned. From these tables and figures,the local Nusselt number and the local Sherwood number change with the variations of λ,ξ,Nt,and Nb.Generally,while the local Nusselt number decreases asσincreases,the local Sherwood number increases with increasing σ. Further,according to Figs. 2−5,the local Nusselt number and the local Sherwood number change monotonically with the change in λ. The range of σfor which the solution exists increases as λincreases. For an increasing slip parameter at the boundary,the generation of vorticity for shrinking velocity is slightly reduced [23] . Therefore,with the imposed suction,that vorticity remains confined in the boundary layer region for larger shrinking velocity (i.e.,σ< 0). Hence,the steady solution is possible for some large values of σ.
 |
 |
 |
| Fig. 2 Variations of local Nusselt number withσ for different values of λ(s=3, ξ=0.5,Nt=Nb=0.5,Le=2,Pr6.8) |
 |
| Fig. 3 Variations of local Sherwood number with σ for different values of λ (s=3, ξ=0.5,Nt=Nb=0.5,Le=2,Pr6.8) |
Contrary to λ,σc remains unchanged for different values of ξ. This is clear from (8)-(11) where the thermal field does not affect the flow field. The increasingξyields a decreasing surface heat transfer (see Fig. 4) and encourages mass exchange efficiency at the surface (see Fig. 5). In both figures,we can see that the values change monotonically with the increasing stretching velocity. The effect occurring in surface heat transfer is greater than the effect observed in mass transfer at the surface. For an increase of 50% inξ,the local Nusselt number reduces by 30% while the mass exchange efficiency increases by only 6%. Despite the increasing mass transfer rate,the large drop in the heat transfer rate may prove to be detrimental to the performance of numerous heat transfer heat devices.
 |
| Fig. 4 Variations of local Nusselt number withσfor different values of ξ (s=3, λ=0.1,Nt=Nb=0.5,Le=2,Pr6.8) |
 |
| Fig. 5 Variations of local Sherwood number withσfor different values of ξ (s=3, λ=0.1,Nt=Nb=0.5,Le=2,Pr6.8) |
Tables 2 and 3 depict the effects of thermophoresis and Brownian motion parameter on the local Nusselt number and the local Sherwood number. It is seen from the tables that increasing the thermophoresis parameterNtis to reduce both the local Nusselt and Sherwood numbers. It is noted thatNthas more significant effect on the local Sherwood number than the local Nusselt number. Applying different Brownian motion parameterNbto the problem however produces several outcomes. As stated previously,in general,the local Nusselt number decreases with increasing σ. Nevertheless,it seems that for Nb=0.3 and Nb=0.4,the local Nusselt number increases with increasing σ. On the other hand,increasingNbresults in an increase in the local Sherwood number but reduces the surface heat transfer (i.e.,local Nusselt number). AsNb andNtincrease,the thermal boundary layer thickness increases too. The thickening boundary layer causes the local Nusselt number to drop. Furthermore,it is observed that for all values of parameters,we obtain θ' (0)>0,which indicates that the heat is transferred from the hot surface to the cool fluid.
The samples of velocity,temperature,and concentration profiles are included in Figs 6-8. These profiles satisfy the far field boundary condition (11) asymptotically,which support the numerical results obtained besides supporting the existence of dual solutions shown in Figs 2-5. Figure 6 shows that for an increased λ,the velocity increases. However,in Fig. 7,it is observed that the temperature decreases as λincreases. Due to the dependency of concentration on the temperature field,it is expected that higher λprevents concentration from penetrating further, and hence the concentration decreases as λincreases as seen in Fig. 8.
 |
| Fig. 6 Velocity profiles for different values of λwhen s=3 and σ=−0.1 |
 |
| Fig. 7 Temperature profiles for different values of λwhens=3,ξ=0.5,Nb=Nt =0.5,Le=2,σ=−0.1,andPr6.8 |
 |
| Fig. 8 Concentration profiles for different values of λ(s=3,ξ=0.5,Nb=Nt=0.5,Le=2,σ=−0.1, Pr6.8) |
The boundary layer flow of a nanofluid past a stretching/shrinking sheet with a hydrodynamic and thermal slip boundary conditions is studied. Numerical solutions to the governing equations are obtained using a shooting method. The values of the skin friction coefficient and the local Nusselt number decrease as the stretching/shrinking parameter increases. On the other hand,the local Sherwood number increases with increasing the stretching/shrinking parameter. The range of the stretching/shrinking parameter for which the solution exists increases as velocity slip parameter λincreases. The local Nusselt number diminishes as thermal slip parameterξincreases. As opposed to this,the local Sherwood number increases with increasing the thermal slip parameter. Increasing the thermophoresis parameter is to decrease the local Nusselt number and the local Sherwood number. Furthermore,an increase in the Brownian motion parameter results in increasing manner of the local Sherwood number,but decreases the local Nusselt number.
Acknowledgements The authors wish to thank the anonymous reviewers for their valuable comments and suggestions.
| [1] | Choi, S. U. S. Enhancing thermal conductivity of fluids with nanoparticle. Developments andApplications of Non-Newtonian Flows (eds. Siginer, D. A. and Wang, H. P.), American Societyof Mechanical Engineers, Central Michigan University, 99-105 (1995) |
| [2] | Masuda, H., Ebata, A., Teramae, K., and Hishinuma, N. Alteration of thermal conductivity andviscosity of liquid by dispersing ultra-fine particles. Netsu Bussei, 7, 227-233 (1993) |
| [3] | Xuan, Y. and Li, Q. Heat transfer enhancement of nanofluids. International Journal of Heat andFluid Flow, 21, 58-64 (2000) |
| [4] | Xuan, Y. and Roetzel, W. Conceptions for heat transfer correlation of nanofluids. InternationalJournal of Heat and Mass Transfer, 43, 3701-3707 (2000) |
| [5] | Rahman, M. M., Al-Lawatia, M. A., Eltayeb, I. A., and Al-Salti, N. Hydromagnetic slip flow ofwater based nanofluids past a wedge with convective surface in the presence of heat generation(or) absorption. International Journal of Thermal Sciences, 57, 172-182 (2012) |
| [6] | Lee, S., Choi, S. U. S., Li, S., and Eastman, J. A. Measuring thermal conductivity of fluidscontaining oxide nanoparticles. Journal of Heat Transfer, 121, 280-289 (1999) |
| [7] | Buongiorno, J. Convective transport in nanofluid. Journal of Heat Transfer, 128, 240-250 (2006) |
| [8] | Nield, D. A. and Kuznetsov, A. V. The Cheng-Minkowycz problem for natural convectiveboundary-layer flow in a porous medium saturated by a nanofluid. International Journal of Heatand Mass Transfer, 52, 5792-5795 (2009) |
| [9] | Nield, D. A. and Kuznetsov, A. V. The Cheng-Minkowycz problem for the double-diffusive naturalconvective boundary layer flow in a porous medium saturated by a nanofluid. International Journalof Heat and Mass Transfer, 54, 374-378 (2011) |
| [10] | Kuznetsov, A. V. and Nield, D. A. Natural convective boundary-layer flow of a nanofluid past avertical plate. International Journal of Thermal Sciences, 49, 243-247 (2010) |
| [11] | Kuznetsov, A. V. and Nield, D. A. Double-diffusive natural convective boundary-layer flow of ananofluid past a vertical plate. International Journal of Thermal Sciences, 50, 712-717 (2011) |
| [12] | Khan, W. A. and Pop, I. Boundary-layer flow of a nanofluid past a stretching sheet. InternationalJournal of Heat and Mass Transfer, 53, 2477-2483 (2010) |
| [13] | Makinde, O. D. and Aziz, A. Boundary layer flow of a nanofluid past a stretching sheet with aconvective boundary condition. International Journal of Thermal Sciences, 50, 1326-1332 (2011) |
| [14] | Fischer, E. G. Extrusion of Plastics, Wiley, New York (1976) |
| [15] | Crane, L. J. Flow past a stretching plate. Journal of Applied Mathematics and Physics, 21, 645-647 (1970) |
| [16] | Wang, C. Y. Analysis of viscous flow due to a stretching sheet with surface slip and suction.Nonlinear Analysis: Real World Applications, 10, 375-380 (2009) |
| [17] | Salari, M., Mohammadtabar, M., and Mohammadtabar, A. Numerical solutions to heat transferof nanofluid flow over stretching sheet subjected to variations of nanoparticle volume fraction andwall temperature. Appl. Math. Mech. -Engl. Ed., 35, 63-72 (2014) DOI 10.1007/s10483-014-1772-8 |
| [18] | Mastroberardino, A. Accurate solutions for viscoelastic boundary layer flow and heat transferover stretching sheet. Appl. Math. Mech. -Engl. Ed., 35, 133-142 (2014) DOI 10.1007/s10483-014-1778-7 |
| [19] | Ali, F. M., Nazar, R., Arifin, N. M., and Pop I. Mixed convection stagnation-point flow on verticalstretching sheet with external magnetic field. Appl. Math. Mech. -Engl. Ed., 35, 155-166 (2014)DOI 10.1007/s10483-014-1780-8 |
| [20] | Miklavčič, M. and Wang, C. Y. Viscous flow due to a shrinking sheet. Quarterly of AppliedMathematics, 64, 283-290 (2006) |
| [21] | Wang, C. Y. Stagnation flow towards a shrinking sheet. International Journal of Non-LinearMechanics, 43, 377-382 (2008) |
| [22] | Fang, T., Yao, S., Zhang, J., and Aziz, A. Viscous flow over a shrinking sheet with a second orderslip flow model. International Journal of Non-Linear Mechanics, 15, 1831-1842 (2010) |
| [23] | Bhattacharyya, K., Mukhopadhyay, S., and Layek, G. C. Slip effects on boundary layer stagnationpointflow and heat transfer towards a shrinking sheet. International Journal of Heat and MassTransfer, 54, 308-313 (2011) |
| [24] | Weidman, P. D., Kubitschek, D. G., and Davis, A. M. J. The effect of transpiration on selfsimilarboundary layer flow over moving surfaces. International Journal of Engineering Science,44, 730-737 (2006) |
| [25] | Postelnicu, A. and Pop, I. Falkner-Skan boundary layer flow of a power-law fluid past a stretchingwedge. Applied Mathematics and Computation, 217, 4359-4368 (2011) |
| [26] | Roşca, A. V. and Pop, I. Flow and heat transfer over a vertical permeable stretching/shrinkingsheet with a second order slip. International Journal of Heat and Mass Transfer, 60, 355-364(2013) |
| [27] | Kumaran, V. and Pop, I. Nearly parallel Blasius flow with slip. Communications in NonlinearScience and Numerical Simulation, 16, 4619-4624 (2011) |
| [28] | Wang, C. Y. Flow due to a stretching boundary with partial slip鈥攁n exact solution of the Navier-Stokes equations. Chemical Engineering Science, 57, 3745-3747 (2002) |
| [29] | Noghrehabadi, A., Pourrajab, R., and Ghalambaz, M. Effect of partial slip boundary condition onthe flow and heat transfer of nanofluids past stretching sheet prescribed constant wall temperature.International Journal of Thermal Sciences, 54, 253-261 (2012) |
| [30] | Sharma, R., Ishak, A., and Pop, I. Partial slip flow and heat transfer over a stretching sheet in ananofluid. Mathematical Problems in Engineering, 7, 724547 (2013) |
| [31] | Aman, F., Ishak, A., and Pop, I. Mixed convection boundary layer flow near stagnationpointon vertical surface with slip. Appl. Math. Mech. -Engl. Ed., 32, 1599-1606 (2011) DOI10.1007/s10483-011-1526-x |
| [32] | Buongiorno, J., and Hu, W. Nanofluid coolants for advanced nuclear power plants. Proceedings ofICAPP ' 05, Seoul (2005) |
| [33] | Khan, W. A., Uddin, M. J., and Ismail, A. I. M. Hydrodynamic and thermal slip effect on doublediffusivefree convective boundary layer flow of a nanofluid past a flat vertical plate in the movingfree stream. PLOS ONE, 8, e54024 (2013) |
| [34] | Bachok, N., Ishak, A., and Pop, I. Flow and heat transfer characteristics on a moving plate in ananofluid. International Journal of Heat and Mass Transfer, 55, 642-648 (2012) |
| [35] | Fang, T. and Zhang, J. Thermal boundary layers over a shrinking sheet: an analytical solution.Acta Mechanica, 209, 325-343 (2010) |
 2014, Vol. 35
2014, Vol. 35















 for different values of sand λ
for different values of sand λ