Shanghai University
Article Information
- Chen AN, Jian SU . 2014.
- Dynamic response of axially moving Timoshenko beams: integral transform solution
- Appl. Math. Mech. -Engl. Ed., 35(11): 1421-1436
- http://dx.doi.org/10.1007/s10483-014-1879-7
Article History
- Received 2014-1-1;
- in final form 2014-3-15
2 Nuclear Engineering Program, COPPE, Universidade Federal do Rio de Janeiro, CP 68509, Rio de Janeiro 21941-972, Brazil
Transverse vibration problems of axially moving beams received a lot attention due to its association with various applications,such as band saw blades,textile machines,power transmission belts,high-speed magnetic tapes,and fluid conveying pipes.
Many analytical methods and numerical approaches have been used to study the vibration behavior and dynamic characteristics of axially moving beams. Pakdemirli et al.[1] investigated the non-linear transverse vibrations of an axially moving Euler-Bernoulli beam,where the multiple-scale method was employed to the motion equation for finding approximate solutions. Yang and Chen[2] analyzed the stability of an axially moving viscoelastic beam with simply supported ends and with pulsating speed,where the Galerkin method and the averaging approach were used to investigate the instability interval of the subharmonic resonance and the combination of resonances for the axially moving beam. Lee and Oh[3] proposed a spectral element model for the transverse response of an axially moving viscoelastic beam,and conducted numerical studies to analyze the viscoelasticity effect on the dynamic characteristics and stability of the moving beams. Liu and Deng[4] introduced a subspace-based identification algorithm to obtain the pseudo-modal parameters of an axially moving cantilever beam, and checked the capabilities of the algorithm by comparing the results with the ones observed from the experimental study. By means of Newton’s second law,Chen and Yang[5] defined the governing equation of nonlinear vibration of axially moving beams,obtained the integropartial- differential formulation through replacing the axial tension by its average over the full beam length,and evaluated the natural frequencies using the multiple-scale method. Jakšić[6] presented a numerical algorithm for the solution of natural frequencies of axially moving beams, the validity of which was proved by comparing the calculated results with the analytical solutions of its limiting cases. Ponomareva and van Horssen[7] studied the transverse vibration of an axially moving beam by adopting a combined model that is a string model at lower frequencies and a stretched beam model at higher frequencies. Based on the Hamilton principle and the finite element method,Chang et al.[8] derived the governing equations of an axially moving Rayleigh beam,the natural frequencies and the transverse response of which were obtained from the eigenvalue problem and by using the time integration method,respectively. Huang et al.[9] examined the nonlinear vibration behavior of an axially moving beam with periodic excitation. The incremental harmonic balance method and the multivariable Floquet theory were employed to evaluate the dynamic behavior and the stability of the system,respectively. Wang[10] investigated the weakly forced vibration of an axially accelerating beam defined by the standard linear solid model,and used the multiple-scale method to analyze the steady-state response. Marynowski[11] investigated the dynamics of the axially moving sandwich beams with elastic faces and a viscoelastic core,where the two-parameter Kelvin-Voigt rheological model was employed to define the material characteristics of the core.
In order to take into account the shear deformation and rotational inertia effects for nonslender beams,there are also comprehensive studies based on the Timoshenko theory. Lee et al.[12] presented a spectral element model for the axially moving Timoshenko beam,and analyzed the effects of the axial speed and the axial tension on the vibration behaviour and stability of the moving beam. To investigate the vibration response of the railway track due to a moving train,Cojocaru et al.[13] modeled the train as a Timoshenko beam with distributed stiffness moving at a constant velocity,where the derived eighth-order system of ODEs was solved by the mathematical software Maple. Using the Galerkin method,Yang et al.[14] discretized the governing equation for transverse vibration of a simply-supported axially accelerating Timoshenko beam,and analyzed the instability conditions of the system by the averaging method. Tang et al.[15] investigated vibration characteristics and critical speed of axially moving Timoshenko beams,the results of which were compared to the ones for Rayleigh beams,shear beams and Euler-Bernoulli beams. Tang et al.[16] extended their previous work by performing the parametric resonance analysis of axially moving Timoshenko beams with variable velocity, where the multiple-scale method was applied to study the steady-state behavior. Subsequently, Tang et al.[17] studied the nonlinear vibration of simply-supported axially moving Timoshenko beams under external excitations,and adopted the multiple-scale method to consider superharmonic resonance and subharmonic resonance. Moreover,the results of nonlinear transverse vibration of an axially moving Timoshenko beam with two free edges were reported by Li et al.[18]. To avoid the approximate boundary conditions in previous studies,Tang et al.[19] derived the governing equations for axially accelerating viscoelastic Timoshenko beams with the accurate boundary conditions by means of the generalized Hamilton principle. Ghayesh and Balar[20] obtained two dynamic models of axially moving Timoshenko beams including one regarding only the transverse displacement and the other regarding both longitudinal and transverse displacements,and employed the multiple-scale method to obtain the natural frequencies and steady-state behaviour of the system. By considering the longitudinal,transverse, and rotational displacements,Ghayesh and Amabili[21] investigated the three-dimensional nonlinear dynamic phenomenon of axially moving Timoshenko beams,and solved the reduced set of nonlinear ODEs using the direct time integration method and pseudo-arclength continuation technique.
Recently,a semi-analytical numerical approach,known as the generalized integral transform technique (GITT),has been well developed in the understanding of heat transfer and fluid flow phenomenons[22,23,24]. The feature of automatic global error control in this method makes it quite suitable for benchmarking. The GITT has been applied in analyzing the bending problem of orthotropic plates[25],solving the dynamic response of axially moving strings[26],axially moving beams[27],fluid-conveying pipes[28],and predicting the vortex-induced vibration of long flexible cylinders[29],which demonstrated high accuracy,excellent convergence behavior,and good longtime numerical stability of the approach.
To our best knowledge,the dynamic response of axially moving Timoshenko beams has not been studied using the GITT. Due to the lack of study in this area,the GITT approach is used to investigate the dynamic behavior of axially moving Timoshenko beams subjected to the following two types of boundary conditions,respectively: (i) clamped-clamped and (ii) simplysupported. The paper is organized as follows. Section 2 defines the problem. In Section 3,the semi-analytical numerical solution is given by performing integral transform. The numerical results of proposed method,such as the transverse deflections and the angles of rotation are presented in Section 4. A parameter study is then performed to investigate the effects of the axial speed,the axial force and the amplitude of external distributed force on the dynamic behavior of axially moving Timoshenko beams. Finally,the paper ends in Section 5 with conclusions and perspectives. 2 Mathematical formulation
Consider an axially moving Timoshenko beam with constant velocity c in the x direction, as illustrated in Fig. 1,with length L,density ρ,cross-sectional area A,moment of inertia I,shear coefficient κ,modulus of elasticity E,axial tension Nx,and shear modulus G. The transverse displacement and the angle of rotation due to bending are indicated by w(x,t) and θ(x,t),respectively. The governing equations of transverse motion of an axially moving uniform Timoshenko beam can be derived as follows[12]:
 |
| Fig. 1 Illustration of axially moving Timoshenko beam |
Two types of boundary conditions are considered: (i) clamped-clamped,
and (ii) simply-supported,By substituting dimensionless variables and parameters,
into (1)-(4),the dimensionless governing equation can be obtained as follows (dropping the superposed asterisks for simplicity): with the dimensionless clamped-clamped boundary conditions and the dimensionless simply-supported boundary conditions respectively. The initial conditions are defined in the dimensionless form as follows: 3 Integral transform solutionOn the basis of the principle of the GITT,the additional eigenvalue problem should be selected for the dimensionless governing equations (6) and (7) with the homogeneous boundary conditions (8) or (9). For the clamped-clamped boundary conditions,the spatial coordinate ‘x’ is eliminated through integral transformation. The related eigenvalue problems are adopted for the transverse deflection as follows:
with the following boundary conditions and for the angle of rotation as follows: with the following boundary conditions respectively,where Xi,μi,and Yi,φi are the eigenfunctions and eigenvalues of problems (11) and (12),satisfying the following orthogonality properties:Problems (13) and (14) are readily solved analytically to yield
and the eigenvalues becomeThe norms,or normalization integrals,are written as
For the simply-supported boundary conditions,the related eigenvalue problem for the transverse deflection is the same as the one above mentioned,while the eigenvalue problem for the angle of rotation is defined as follows:
with the following boundary conditions where Zi and ψi are the eigenfunctions and eigenvalues of problems (21),satisfying the following orthogonality property:Problem (22) is readily solved analytically to yield
and the eigenvalues becomeThe norms,or normalization integrals,are written as
The eigenvalue problems (11),(12),and (21) allow to establish the following integral transform pair for the transverse deflection and the angle of rotation:
where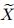 i(ξ) and
i(ξ) and 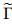 i(ξ) are the normalized eigenfunctions
Now,to carry out the integral transform,the dimensionless equations (6) and (7) are multiplied
by the operator
i(ξ) are the normalized eigenfunctions
Now,to carry out the integral transform,the dimensionless equations (6) and (7) are multiplied
by the operator 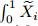 (ξ)dξ and
(ξ)dξ and 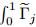 (ξ)dξ,respectively,where the inverse formulas (26b)
and (26d) are applied. After some derivation,the following set of ODEs can be obtained:
where the coefficients are given from the following integrals:
and λj equals to φj and ψj for the clamped-clamped and simply-supported boundary conditions,
respectively.
(ξ)dξ,respectively,where the inverse formulas (26b)
and (26d) are applied. After some derivation,the following set of ODEs can be obtained:
where the coefficients are given from the following integrals:
and λj equals to φj and ψj for the clamped-clamped and simply-supported boundary conditions,
respectively.
Similarly,initial conditions (10) are also integral transformed through the operator,generating
For computational purposes,the expansions for the transverse deflection and the angle of
rotation are truncated to finite orders NW and NA,respectively. (27) and (28) in the truncated
series are subsequently calculated by the NDSolve routine of Mathematica[30]. Once the
transformed potential, i and
i and  j ,the numerically evaluated,the inversion formulas (26b) and
(26d) are then used to yield the explicit analytical expressions for the dimensionless transverse
deflection w(ξ,τ) and the angle of rotation θ(ξ,τ).
4 Results and discussion
j ,the numerically evaluated,the inversion formulas (26b) and
(26d) are then used to yield the explicit analytical expressions for the dimensionless transverse
deflection w(ξ,τ) and the angle of rotation θ(ξ,τ).
4 Results and discussion
We now present the convergence behavior of numerical results for the dimensionless transverse deflection w(ξ,τ) and the angle of rotation θ(ξ,τ) of an axially moving Timoshenko beam calculated by the GITT approach. For the case examined,the following dimensionless parameters are taken in (6) and (7):

The solution of the systems (27) and (28) is obtained with NW ≤ 160 and NA ≤ 60 to analyze the convergence behavior.
The dimensionless transverse displacement w(ξ,τ) and the angle of rotation θ(ξ,τ) at different positions,ξ = 0.1,0.3,0.5,0.7,and 0.9,of an axially moving Timoshenko beam with clamped-clamped boundary conditions are presented in Tables 1 and 2,respectively. The convergence behavior of the GITT solution is studied for increasing truncation orders NW = 40, 80,120,160 and NA = 40,60 at τ = 5,20,50,respectively. For the transverse deflection of clamped-clamped axially moving Timoshenko beams,convergence is basically achieved at some points with truncation orders (NW ≤ 40) and (NA ≤ 40). For the convergence achieved at most points,more terms (e.g.,NW = 80 and NA = 40) are required. For the angle of rotation of the moving beam with clamped-clamped boundary conditions,the convergence is also achieved essentially at most points with truncation orders NW = 80 and NA = 40. The results at τ = 50 show that the good convergence behavior of the GITT solution does not change with time,considered as a long-time stability proof. The convergence behaviors of the transverse deflection and the angle of rotation of axially moving beams with simply-supported boundary conditions are given in Tables 3 and 4. Figures 2 and 3 present the GITT results with different truncation orders NW for time history of the transverse deflection at τ ∈ [15, 20] and τ ∈ [35, 40] of axially moving Timoshenko beams with clamped-clamped and simply-supported boundary conditions, respectively. The good convergence behavior of our method is clearly exhibited.
 |
 |
 |
 |
 |
| Fig. 2 GITT solutions with different truncation orders NW for time history of dimensionless transverse deflection at τ ∈ [15, 20] and τ ∈ [35, 40] of axially moving Timoshenko beam with clamped-clamped boundary conditions (α = 1.0,η = 1.0,β = 1.0,γ = 1.0,and v = 0.8) |
 |
| Fig. 3 GITT solutions with different truncation orders NW for time history of dimensionless transverse deflection at τ ∈ [15, 20] and τ ∈ [35, 40] of axially moving Timoshenko beam with simply-supported boundary conditions (α = 1.0,η = 1.0,β = 1.0,γ = 1.0,and v = 0.8) |
The dynamic response is obtained at different moving speed. Figures 4 and 5 show the effect of the axial speed (v = 0.1,0.5,0.7,and 1.0) on the transverse deflection at the central point of the axially moving Timoshenko beam with clamped-clamped and simply-supported boundary conditions,respectively,while α = 1.0,β = 1.0,γ = 1.0,and η = 1.0. It can be seen that the amplitudes of vibration do not vary monotonously with the axial speed. When v = 0.7,the maximum absolute value of the transverse deflection is 0.265 60,much higher than the results obtained with v = 0.1,0.5,and 1.0. For the vibration with v = 0.7,the amplitude builds up and then dies down in a regular pattern,which is clearly the occurrence of the beating phenomenon. Figures 6 and 7 show the effect of the axial force (α = 1.0,1.5,1.8,and 2.0) on the transverse deflection at the central point of the axially moving Timoshenko beam with clamped-clamped and simply-supported boundary conditions,respectively,while β = 1.0,γ = 1.0,η = 1.0,and v = 0.8. It can be seen that for both cases,the maximum absolute amplitude value of the system decreases with the axial force. Finally,the effect of the amplitude of external distributed force (η = 1.0,1.5,1.8,and 2.0) on the dimensionless transverse deflection at the central point of an axially moving Timoshenko beam is examined,where α = 1.0,β = 1.0,γ = 1.0,and v = 0.8 are employed,as shown in Figs. 8 and 9. It can be clearly seen that the maximum absolute amplitude value of the system increases proportionally with increasing amplitude of external distributed force for both clamp-clamped and simply-supported cases.
 |
| Fig. 4 Effect of axial speed v on transverse deflection at central point of axially moving Timoshenko beam with clamped-clamped boundary conditions: (a) v = 0.1,(b) v = 0.5,(c) v = 0.7,and (d) v = 1.0 |
 |
| Fig. 5 Effect of axial speed v on transverse deflection at central point of axially moving Timoshenko beam with simply-supported boundary conditions: (a) v = 0.1,(b) v = 0.5,(c) v = 0.7,and (d) v = 1.0 |
 |
| Fig. 6 Effect of axial force α on transverse deflection at central point of axially moving Timoshenko beam with clamped-clamped boundary conditions: (a) α = 1.0,(b) α = 1.5,(c) α = 1.8,and (d) α = 2.0 |
 |
| Fig. 7 Effect of axial force α on transverse deflection at central point of axially moving Timoshenko beam with simply-supported boundary conditions: (a) α = 1.0,(b) α = 1.5,(c) α = 1.8,and (d) α = 2.0 |
 |
| Fig. 8 Effect of amplitude of external distributed force η on dimensionless transverse deflection at central point of axially moving Timoshenko beam with clamped-clamped boundary conditions: (a) η = 1.0,(b) η = 1.5,(c) η = 1.8,and (d) η = 2.0 |
 |
| Fig. 9 Effect of amplitude of external distributed force η on dimensionless transverse deflection at central point of axially moving Timoshenko beam with simply-supported boundary conditions: (a) η = 1.0,(b) η = 1.5,(c) η = 1.8,and (d) η = 2.0 |
The GITT has shown in this study to be a practical method for the analysis of vibration behavior of axially moving Timoshenko beams,providing a semi-analytical numerical solution for the transverse deflection and the angle of rotation. The solutions for both clamped-clamped and simply-supported cases converge essentially at truncation orders (NW ≤ 80 and NA ≤ 40). Good long-time stability is also shown. The parametric study indicates that,the maximum absolute amplitude values of the system do not vary monotonously with the axial speed,and the beating phenomenon can occur at a certain value of the axial speed (e.g.,v = 0.7). Besides,the maximum absolute amplitude value of the system decreases with the axial force and increases proportionally with the amplitude of external distributed force. The proposed approach can be employed to predict the dynamic response of axially moving viscoelastic Timoshenko beams for future investigation.
| [1] | Pakdemirli, H. R., Öz, M., and Boyaci, H. Non-linear vibrations and stability of an axially movingbeam with time-dependent velocity. International Journal of Non-Linear Mechanics, 36(1), 107-115 (2001) |
| [2] | Yang, X. D. and Chen, L. Q. Dynamic stability of axially moving viscoelastic beams with pulsatingspeed. Appl. Math. Mech. -Engl. Ed., 26(8), 989-995 (2005) DOI 10.1007/BF02466411 |
| [3] | Lee, U. and Oh, H. Dynamics of an axially moving viscoelastic beam subject to axial tension.International Journal of Solids and Structures, 42(8), 2381-2398 (2005) |
| [4] | Liu, K. F. and Deng, L. Y. Identification of pseudo-natural frequencies of an axially movingcantilever beam using a subspace-based algorithm. Mechanical Systems and Signal Processing,20(1), 94-113 (2006) |
| [5] | Chen, L. Q. and Yang, X. D. Nonlinear free transverse vibration of an axially moving beam:comparison of two models. Journal of Sound and Vibration, 299(1-2), 348-354 (2007) |
| [6] | Jakšić, N. Numerical algorithm for natural frequencies computation of an axially moving beammodel. Meccanica, 44(6), 687-695 (2009) |
| [7] | Ponomareva, S. V. and van Horssen, W. T. On the transversal vibrations of an axially movingcontinuum with a time-varying velocity: transient from string to beam behavior. Journal of Soundand Vibration, 325(4-5), 959-973 (2009) |
| [8] | Chang, J. R., Lin, W. J., Huang, C. J., and Choi, S. T. Vibration and stability of an axiallymoving rayleigh beam. Applied Mathematical Modelling, 34(6), 1482-1497 (2010) |
| [9] | Huang, J. L., Su, R. K. L., Li, W. H., and Chen, S. H. Stability and bifurcation of an axiallymoving beam tuned to three-to-one internal resonances. Journal of Sound and Vibration, 330(3),471-485 (2011) |
| [10] | Wang, B. Asymptotic analysis on weakly forced vibration of axially moving viscoelastic beamconstituted by standard linear solid model. Appl. Math. Mech. -Engl. Ed., 33(6), 817-828 (2012)DOI 10.1007/s10483-012-1588-8 |
| [11] | Marynowski, K. Dynamic analysis of an axially moving sandwich beam with viscoelastic core.Composite Structures, 94(9), 2931-2936 (2012) |
| [12] | Lee, U., Kim, J., and Oh, H. Spectral analysis for the transverse vibration of an axially movingTimoshenko beam. Journal of Sound and Vibration, 271(3-5), 685-703 (2004) |
| [13] | Cojocaru, E. C., Irschik, H., and Schlacher, K. Concentrations of pressure between an elasticallysupported beam and a moving Timoshenko-beam. Journal of Engineering Mechanics-ASCE,129(9), 1076-1082 (2003) |
| [14] | Yang, X. D., Tang, Y. Q., Chen, L. Q., and Lim, C. W. Dynamic stability of axially acceleratingTimoshenko beam: averaging method. European Journal of Mechanics A-Solids, 29(1), 81-90(2010) |
| [15] | Tang, Y. Q., Chen, L. Q., and Yang, X. D. Natural frequencies, modes and critical speeds ofaxially moving Timoshenko beams with different boundary conditions. International Journal ofMechanical Sciences, 50(10-11), 1448-1458 (2008) |
| [16] | Tang, Y. Q., Chen, L. Q., and Yang, X. D. Parametric resonance of axially moving Timoshenkobeams with time-dependent speed. Nonlinear Dynamics, 58(4), 715-724 (2009) |
| [17] | Tang, Y. Q., Chen, L. Q., and Yang, X. D. Nonlinear vibrations of axially moving Timoshenkobeams under weak and strong external excitations. Journal of Sound and Vibration, 320(4-5),1078-1099 (2009) |
| [18] | Li, B., Tang, Y. Q., and Chen, L. Q. Nonlinear free transverse vibrations of axially movingTimoshenko beams with two free ends. Science China-Technological Sciences, 54(8), 1966-1976(2011) |
| [19] | Tang, Y. Q., Chen, L. Q., Zhang, H. J., and Yang, S. P. Stability of axially accelerating viscoelasticTimoshenko beams: recognition of longitudinally varying tensions. Mechanism and MachineTheory, 62, 31-50 (2013) |
| [20] | Ghayesh, M. H. and Balar, S. Non-linear parametric vibration and stability analysis for twodynamic models of axially moving Timoshenko beams. Applied Mathematical Modelling, 34(10),2850-2859 (2010) |
| [21] | Ghayesh, M. H. and Amabili, M. Three-dimensional nonlinear planar dynamics of an axiallymoving Timoshenko beam. Archive of Applied Mechanics, 83(4), 591-604 (2013) |
| [22] | Cotta, R. M. Integral Transforms in Computational Heat and Fluid Flow, CRC Press, Boca Raton(1993) |
| [23] | Cotta, R. M. and Mikhailov, M. D. Heat Conduction——Lumped Analysis, Integral Transforms,Symbolic Computation, John Wiley & Sons, Chichester, England (1997) |
| [24] | Cotta, R. M. The Integral Transform Method in Thermal and Fluids Science and Engineering,Begell House, New York (1998) |
| [25] | An, C., Gu, J. J., and Su, J. Integral transform solution of bending problem of clamped orthotropicrectangular plates. International Conference on Mathematics and Computational Methods Appliedto Nuclear Science and Engineering, Rio de Janeiro, Brazil (2011) |
| [26] | Ma, J. K., Su, J., Lu, C. H., and Li, J. M. Integral transform solution of the transverse vibration ofan axial moving string. Journal of Vibration, Measurement & Diagnosis, 26(117), 104-107 (2006) |
| [27] | An, C. and Su, J. Dynamic response of clamped axially moving beams: integral transform solution.Applied Mathematics and Computation, 218(2), 249-259 (2011) |
| [28] | Gu, J. J., An, C., Duan, M. L., Levi, C., and Su, J. Integral transform solutions of dynamicresponse of a clamped-clamped pipe conveying fluid. Nuclear Engineering and Design, 254, 237-245 (2013) |
| [29] | Gu, J. J., An, C., Levi, C., and Su, J. Prediction of vortex-induced vibration of long flexiblecylinders modeled by a coupled nonlinear oscillator: integral transform solution. Journal of Hydrodynamics,24(6), 888-898 (2012) |
| [30] | Wolfram, S. The Mathematica Book, 5th ed., Wolfram Media/Cambridge University Press, Champaign(2003) |
 2014, Vol. 35
2014, Vol. 35






























