Shanghai University
Article Information
- Zi-xing LU, Qiang LIU, Xin CHEN. 2014.
- Analysis and simulation for tensile behavior of anisotropic open-cell elastic foams
- Appl. Math. Mech. -Engl. Ed., 35(11): 1437-1446
- http://dx.doi.org/10.1007/s10483-014-1874-7
Article History
- Received 2013-10-20;
- in final form 2014-3-10
Low-density open-cell foams have a complex microstructure consisting of a space interconnected network of struts. Lots of experiments[1,2,3] illustrated that the cells of most foams would be elongated obviously along a certain direction (rise direction) that always evolve during the foaming process. This geometric anisotropy of cells has a significant effect on the mechanical properties of open-cell foams. Gong and Kyriakides[1] presented the geometric information about a class of open-cell polyester urethane foams,which included the cell and strut geometry and distribution of solid material along the struts,as well as the anisotropy ratio tested ranging from 1.2 to 1.5 generally. As to open-cell aluminum foams,Perrot et al.[3] obtained the value 1.26-1.56 for the aspect ratio. However,most of previous works focus on the research that treated the foams as isotropic ones,as a result,those models failed to represent the realistic microstructure,and thereby the anisotropic mechanic properties. Hence,it is essential to investigate the effect of anisotropy on the mechanical properties of foams with the more appropriate models.
On the issue of anisotropy in the open-cell foams,previous researchers have conducted some works[4,5,6]. Recently,with the development of studies about the mechanic behavior of foams, the issue of foam anisotropy has attracted more concerns. Lu et al.[7,8,9,10] investigated the effect of anisotropy on elastic properties as well as compression in large deformation of open-cell foams by constructing the anisotropic Voronoi random model and Kelvin model which all could represent properly both the cell structure and the anisotropy in realistic foams. Especially,the elongated Kelvin model they proposed can reflect the anisotropy of open-cell foams based on the regular Kelvin model and can be used to analyze the high strain compressive behavior[10]. Gong and Kyriakides[1] predicted the initial elastic constants and closed form expressions on the basis of a series of polyester urethane open-cell foams. The results demonstrated that inclusion of the geometric complexities is essential for successful prediction of the mechanical properties of the foams. In addition,the nonlinear parts of the response including the foam crushing behavior were also analyzed[11]. These researches all concerned on the compressive properties for that foams are always designed to support compressive loads and absorb energy in their applications.
Although it is very significant to comprehend the compressive behavior of foam materials, yet,under some conditions,such as in the sandwich structures and other structural materials, foams are always subjected to tension as well as compression. The existing reports of this area are far less than that for compression,and almost focus on the experimental investigation. Andrews and Gibson[12] described a set of experiments designed to study the tensile strength of open-cell aluminum foams. Kabir et al.[13] studied the tensile and fracture behavior of different polymer foams by performing the tension tests. Recently,Aly[14,15] obtained the behavior of open-cell Ti foams under tension tests and its dependency on their pore sizes,as well as tensile properties of open-cell nickel foams.
Different from the compression deformation,under tension the struts which lie,initially,at an angle to the loading direction,will rotate toward this direction,and the bending moment acting on them will be decreased[5]. Based on the anisotropic elongated Kelvin model[9,10],this paper theoretically analyzed the tensile deformation mechanism,the effect of anisotropy on the tensile stress-strain relationship of open-cell elastic foams,as well as the confirmation by finite element simulation. 2 Anisotropic Kelvin model
As processed in the previous papers[9,10],by elongating the classic Kelvin model in one direction (e.g.,the Z-direction in Fig. 1) and keeping unchanged in the other two directions, the geometric anisotropic Kelvin model could be constructed. Due to the geometric anisotropy, the deformation mechanism is different when the foams are uniaxially stretched. Figure 1 shows the states of cell with different tension directions,where the parameter λ is defined as the anisotropy ratio with λ = tanβ,where β is the angle between the inclined strut and the rise direction. The periodic and symmetric characteristics of Kelvin model mean that it can be simplified properly. The small asymmetric analytical cells for two loading directions are separated respectively and the specific structures are listed in Fig. 2. This kind of cell is bounded by mirror planes that act on the initial and deformed structures.
 |
| Fig. 1 Anisotropic Kelvin model |
 |
| Fig. 2 Simplified structural cell |
Because the two-fold symmetry axis is through the midpoint of the inclined struts in these cells,the curvature and the moment in the midpoint are both zero. Therefore,the half-strut is adopted to analyze the mechanical properties as used in the previous study[16].
It has to be pointed that,the new model in this paper is only adaptive to the lower density elastic open-cell foams. This is because,only the bending deformation of struts is considered in the study and the matrix material is assumed as elasticity,so that the model is suitable to foams with matrix material of rubber or elastic polymer. On the other hand,when the relative density is high,the solid material will accumulate at the joint vertices of struts,affecting the deformation mechanism of the struts. However,in this study,it is assumed that the crosssection area of the strut maintains at a constant along the strut of the cell. Therefore,the analytical solution is adaptive to the low density foams,whose relative density arranges from 0.01 to 0.1. 3 Theoretical analysis 3.1 Loading in rise direction
Take the half-strut OA in Fig. 3 as the object to analyze,where O is the midpoint of the inclined strut AE in Fig. 2(a). A local Cartesian coordinate system Oxz is firstly established on the deformed strut,as shown in Fig. 3. Then,a curvilinear coordinate (s,θ),with origin O,is also established to define the position and analyze the deformation of the half-strut. The parameter θ is the angle between the tangent to the edge and the rise direction. Because the moment at O is zero and a constant force P acts on the strut along the z-direction,the moment at a general position is Px,where the x axis is shown in Fig. 3. According to the elastic deflection theory,the differential equation of the large deflection is
where Es is the Young’s modulus of solid material,and I is the second moment of area of the strut cross-section. |
| Fig. 3 Half-strut element OA |
Differentiating (1) with respect to s and considering the above relation,we get
Multiplying both sides with dθ and integrating from the point O,and utilizing the end condition at O,where the curvature is zero and θ = α,leads to Substituting k2 for P/(EsI),(3) becomes In this anisotropic Kelvin model,the total length of the half-strut OA in Fig. 3 is l',which is Integrating (4) gives where β is the strut inclination angle at the end point A. Then,cos(α/2) is abbreviated by the symbol p and a new variable φ is introduced as that Differentiating (7) gives Substituting (7) and (8) into (6) gives the elliptical integral F (α),i.e., where the elliptic integral F(α) is a function of the inclination angle α of the point O,and the upper limit of integration is The total force 2P acting in the rise direction is related to the applied stress by The above equation shows that as the angle α increases,the integral F(α),the load P,and the stress σz all increase. The vertical projection of the half-strut OA is The initial length of the half-strut OA in the z-direction is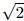 λl/4,so the strain of foams in
the z-direction is
Similarly,in the x-direction the projection dx is sin θds,so
Therefore,the strain in the x-direction is
3.2 Loading in transverse direction
λl/4,so the strain of foams in
the z-direction is
Similarly,in the x-direction the projection dx is sin θds,so
Therefore,the strain in the x-direction is
3.2 Loading in transverse direction
Different from the analysis above,here the inclined struts EA,EB and EC,ED in Fig. 2(b) should be analyzed respectively. Firstly,consider the struts EC and ED. Figure 4 illustrates the deformation of half-strut OC,where O is the midpoint of strut EC. The difference from Fig. 3 is the definitions of angle β and the coordinate. Similarly,the differential equation of the large deflection is
 |
| Fig. 4 Half-strut OC |
And the equations (21) and (22) illustrate that the variables k' and F'(α') are both the functions of the sole argument α'.
To keep the equilibrium,the stress on the upper surface and the lower surface in Fig. 2(b) should be the same,so (20) gives the equation
This means the equation k = k' and givesThe equation above has established the relation between the different arguments α and α',which determines the deformation of the upper and lower inclined struts inside the cell in Fig. 2(b),respectively,hence actually,it is just one independent argument that determines the deformation of the whole cell.
In Fig. 2(b),the length of the deformed cell in the x-direction is
In addition,only inclined struts EC and ED could produce the deformation in the z-direction and only inclined struts EA and EB could produce the deformation in the y-direction,so the lengths of the deformed cell in the z- and y-directions are,respectively, As shown in Fig. 2(b),the lengths of the cell before the deformation in x-,y-,and z-directions are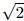 l,2
l,2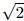 l,and 2
l,and 2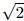 λl,respectively,so the corresponding strains of foams are
λl,respectively,so the corresponding strains of foams are
According to the geometry of the model in Fig. 2,the relative density R of the anisotropic Kelvin model is related to the strut length l and cross section area S by
On the basis of observations on 3D images of the morphology of many synthetic open-cell foams,Jang et al.[2] concluded that the cross section of foams has the characteristic Plateau border shape for the polyester urethane foams and the equilateral triangle or round shape for the aluminum foams. According to the comparison of results of different cross sections by previous researches and considering the feasibility to perform both theoretical analysis and numerical simulation,the equilateral triangle is adopted here as the cross section shape. Then,the second moment of area I is
4 Comparison between theoretical analysis and numerical simulationThe inclination α at the midpoint of the inclined strut is increased by 1 degree gradually, and the elliptic integrals F(α) and F'(α') are evaluated using (9),(17),and (22). The stress is calculated from (11) and (23),and the strain from (13) and (28),with the corresponding curve shown in Fig. 6. To reduce the influence of the solid material on the results,the stress in this paper is expressed in the dimensionless form[7,8],divided by Young’s modulus of solid material and the square of the relative density,hence it becomes independent of the relative density,
To examine the validity of tensile stress-strain curve predicted by theoretical analysis,the anisotropic Kelvin finite element model is established. The strut of low-density foams is assumed to be the uniform cross section straight beam,and the influence of cell anisotropic on the mechanical properties is simulated when the anisotropy ratio λ is 1,1.2,and 1.4,respectively. Consider the combined action of axial,shear,and bending deformations,the FE model in ANSYS is discretized by the BEAM188,the 2-noded 3-D linear finite strain beam based on Timoshenko beam theory. In addition,because of the regularity and periodicity of the selected anisotropic model,the mechanical properties can be evaluated by considering a domain assembled by the regular cells. The domain has periodic boundaries at the three pairs of opposite bounding faces. The two different tensile stress-strain curves are acquired by performing the displacement loads in the rise and transverse directions,respectively.
For the effective simulation,the effect of the model size,defined as the ratio of side length of the domain to that of a single cell,should be reviewed to choose the appropriate size before the simulation[17]. In the previous research[8],we have found that the 4 × 4 × 4 domain can both ensure the sufficient accuracy and save the unnecessary calculation for the high strain deformation. Besides,through the comparison of numerical results of models with different relative densities,it is also found that the numerical results of the relative density R = 0.03 agree best with the dimensionless stress predicted by the theoretical analysis,which is absolutely independent of the relative density. This agreement could be explained by the simplification made in the theoretical analysis: When relative density is too high,the struts could not be treated as the uniform beams; contrarily,when relative density is too low,the error introduced by the numerical simulation could also be amplified. Hence,the relative density R = 0.03 might just represent well the average characteristics of low-density foams.
Figure 5 shows the comparison of our theoretical and numerical results (based on the Kelvin model) and Warren & Kraynik’s results. Using a tetrahedral element to represent the struts intersecting at a node,Warren and Kraynik find,for uniaxial tension,the stress-strain curve could be written as[18]
 |
| Fig. 5 Comparison of results of different methods |
Initially,the elastic response is mainly dominated by the struts bending,so our theoretical analysis agrees better with the finite element analysis. As the tensile strain increases (larger than 30%),the inclined struts become aligned,and the stretching is comparable with the bending. Due to that our theoretical analysis only concerned about the bending deformation mechanism,the predicted results will deviate from the real situation when the strain is large.
Figure 6 shows the comparison between dimensionless tensile stress-strain curves of lowdensity foams with different anisotropy ratios by analytical expressions and numerical simulation. The two graphs in Fig. 6 indicate that as the anisotropy ratio increases,the dimensionless tensile stress-strain curve rises up in the rise direction but go down in the transverse direction. This illustrates that the stiffness has been apparently improved in the rise direction but decrease in the transverse direction. When the tensile stain is not high,the theoretical results agree very well with the numerical results. This also further demonstrated the bending of struts as the dominant deformation mechanism for the tension of low-density open-cell foams. However,as the tensile strain increases,the stress-strain curve of the numerical simulation is gradually lower than that of analytical formula. The main reason that causes the discrepancy is that in the theoretical analysis only the bending of the inclined struts,which was confirmed to play the dominant role during the initial deformation,has been considered,while the axial and shear deformation of these inclined struts,as well as the deformation of other struts which lie in the surface of the cell,have been neglected. And as the struts become aligned,the axial deformation is more obvious. Therefore,when loaded,the overall strain in the theoretical analysis is underestimated,and thus causes a higher stiffness.
 |
| Fig. 6 Dimensionless tensile stress-strain curves of different anisotropy ratios with R = 0.03 (solid: analytical results; hollow: numerical results) |
This study has been concerned with the mechanical response of anisotropic Kelvin model for open-cell elastic foams to uniaxial tension by both theoretical analysis and numerical simulation. Results have indicated that when the tensile strain is not very high,the anisotropic Kelvin model could effectively predict the tensile stress-strain curve of open-cell elastic foams. The conclusions obtained in the present investigation are as follows.
(i) The anisotropy in microstructure has a significant effect on the tensile behavior of opencell foams. As the anisotropy ratio increases,the dimensionless tensile stress-strain curves rise up in the rise direction but go down in the transverse direction.
(ii) The results of the theoretical analysis are close to those of numerical simulation,which confirmed the validity of theoretical analysis. The small discrepancy between them is due to that only bending is taken into consideration in the theoretical analysis.
(iii) As the tensile strain increases,the stress-strain curves predicted by numerical method become gradually lower than those of analytical expression. This is because the proportion of strain produced by the bending deformation decreases when the inclined struts become aligned to the loading axis.
| [1] | Gong, L., Kyriakides, S., and Jang, W. Y. Compressive response of open-cell foams, part I:morphology and elastic properties. International Journal of Solids and Structures, 42, 1355-1379(2005) |
| [2] | Jang, W. Y., Kraynik, A. M., and Kyriakides, S. On the microstructure of open-cell foams and itseffect on elastic properties. International Journal of Solids and Structures, 45, 1845-1875 (2008) |
| [3] | Perrot, C., Panneton, R., and Olny, X. Periodic unit cell reconstruction of porous media: applicationto open-cell aluminum foams. Journal of Applied Physics, 101, 113538 (2007) |
| [4] | Lu, Z., Wang, R., and Huang, Z. A review of studies on the mechanical properties of foam plastics.Advances in Mechanics, 26(3), 306-323 (1996) |
| [5] | Gibson, L. J. and Ashby, M. F. Cellular Solids: Structure & Properties, Pergamon Press, Oxford(1997) |
| [6] | Lu, Z. and Tian, C. Modification of anisotropic model for foam plastics. Chinese Journal of AppliedMechanics, 13(4), 108-111 (1996) |
| [7] | Lu, Z., Zhang, J., and Wang, S. Investigation into elastic properties of anisotropic random foammodel. Journal of Beijing University of Aeronautics and Astronautics, 32(12), 1468-1471 (2006) |
| [8] | Lu, Z., Chen, X., and Zhang, J. Numerical modeling of high strain compression of anisotropicelastic open-cell foams. Journal of Beijing University of Aeronautics and Astronautics, 34(5),564-567 (2008) |
| [9] | Lu, Z., Huang, J., and Chen, X. Elastic properties of anisotropic Kelvin model for open-cell foams.Acta Aeronautica et Astronautica Sinica, 30(6), 1017-1022 (2009) |
| [10] | Lu, Z., Huang, J., and Chen, X. Analysis and simulation of high strain compression of anisotropicopen-cell elastic foams. Science China Technological Sciences, 53(3), 863-869 (2009) |
| [11] | Gong, L. and Kyriakides, S. Compressive response of open cell foams, part II: initiation andevolution of crushing. International Journal of Solids and Structures, 42, 1381-1399 (2005) |
| [12] | Andrews, E. W. and Gibson, L. J. The influence of crack-like defects on the tensile strength of anopen-cell aluminum foam. Scripta Materialia, 44, 1005-1010 (2001) |
| [13] | Kabir, M. E., Saha, M. C., and Jeelani, S. Tensile and fracture behavior of polymer foams.Materials Science and Engineering A, 429, 225-235 (2006) |
| [14] | Aly, M. S. Effect of pore size on the tensile behavior of open-cell Ti foams: experimental results.Materials Letters, 64, 935-937 (2010) |
| [15] | Aly, M. S. Tensile properties of open-cell nickel foams. Materials and Design, 31, 2237-2240 (2010) |
| [16] | Zhu, H. X., Mills, N. J., and Knott, J. F. Analysis of the high strain compression of open-cell.Journal of the Mechanics and Physics of Solid, 45(11-12), 1875-1904 (1997) |
| [17] | Shi, S. and Lu, Z. Finite element analysis for the elastic modulus of open-cell foams based on atetrakaidecahedron model. Journal of Mechanical Strength, 28(1), 108-112 (2006) |
| [18] | Warren, W. E. and Kraynik, A. M. The nonlinear elastic behaviour of open-cell foams. Journalof Applied Mechanics, 58, 376-381 (1991) |
 2014, Vol. 35
2014, Vol. 35

































