Shanghai University
Article Information
- M. H. SHOJAEIFARD, R. TALEBITOOTI, B. RANJBAR, R. AHMADI. 2014.
- Power transmission through double-walled laminated composite panels considering porous layer-air gap insulation
- Appl. Math. Mech. -Engl. Ed., 35(11): 1447-1466
- http://dx.doi.org/10.1007/s10483-014-1877-7
Article History
- Received 2014-2-17;
- in final form 2014-5-29
2 School of Automotive Engineering, Iran University of Science & Technology, Teheran 16844, Iran
Porous materials are known as a passive control element because of their application for reducing the power sound transmission to the structures particularly in high frequency range. In addition,various parameters such as style,shape,easy scalability,and ease of implementation make them useful for engineers. Therefore,they are finding increasing applications in various industries such as aerospace and automotive. In most applications,the porous layers cannot be so effective as a result of improper treatment. Therefore,they should be carefully designed or positioned into the structure.
In the first work,the porous materials are modeled with considering the solid phase to be rigid. In 1956,Biot[1] developed a model that considered shear wave propagation through a solid phase. Bolton and Green[2] and Bolton et al.[3] also introduced a method based on the Biot theory while the porous material was assumed to be homogeneous. This theory has allowed all three waves (two elastic longitudinal waves and one shear (rotational) wave) to propagate in the porous material. Bolton et al.[4] interpreted the macroscopic properties of the porous materials. They successfully showed powerful effects of the porous material and the air gap as a sound insulation. Allard and Atalla[5] initially developed a model to describe the wave propagation in the porous media saturated by heavy fluids. The model was used to predict acoustic performance of the air saturated sound absorbing porous media. Then,they expanded the basic material by reviewing several original topics and adding some new ones in order to integrate the recent developments in the context of wave propagation in porous media and practical numerical prediction methods that are widely used by both researchers and engineers. Cimerman et al.[6] proposed the statistical energy analysis (SEA) model to simulate the sound behavior of vehicle subsystems as sound barriers. Zeng et al.[7] studied the effect of laminated steel body panels on sound pressure level inside a car. They also simulated the SEA model of a vehicle and then compared the transmission loss (TL) of the laminated panels with the conventional one (we use TL to represent the TL parameter). In addition,they indicated that the laminated panels used in automotive components such as roof panel and front dash can reduce the noise of road and driveline. Tadeu et al.[8] investigated the sound insulation provided by single and double panels of steel,concrete,and glass. Onsay[9] proposed the SEA model to investigate some issues such as using it for improving the quality of sound and vibration as well as reducing the cost of mass production. Ghosh et al.[10] presented an experimental setup to address effective performance of the porous material as an insulator. Xin et al.[11] studied the vibration behavior of double-walled acoustic structures. Xin and Lu[12] also studied the TL of orthogonal rib-stiffened double panel structures. Recently,Daneshjou et al.[13] investigated acoustic properties of double-layer composite cylindrical shells by inserting a porous medium between the layers.
Thus,a brief literature review reveals that there is almost no investigation on acoustic transmission of the double-walled laminated composite consisting of two air gaps and porous layers,in spite of the fact that the quantity of TL of the double-walled laminated composite panels is important for their applications. The major differences between the work described here and earlier researches in this field are categorized into reasonable areas of investigation. Firstly,the wave propagation through laminated composite panels in the vicinity of air gap and porous material is a quite new topic. Secondly,the Biot theory is used to model the wave propagation in porous layers in which all wave types are considered. 2 Model description
Figure 1 shows a schematic illustration of wave propagation through a double composite panel with thicknesses of hp1 and hp2. These panels are composed of one porous layer (hfoam) and one air gap (hgap) as an interlaminar treatment. The composite panel is excited with a plane wave of angle γ.
 |
| Fig. 1 Wave propagation through composite panel |
Physical and geometrical characteristics of the construction layers are listed in Table 1. In addition,material properties of the composite layers are presented in Table 2,where the plies are arranged in a [0°,90°,45°,−45°,0°]s pattern. The TL of the structure,as a design parameter, is predicted using analytical and SEA models. Then,the effects of physical parameters as well as those of boundary conditions are investigated.
Based on the model proposed by Biot for theoretical porous materials[1],the dynamic equations, and the stress-strain relations of the porous materials,the equation of wave propagation is calculated for these materials from the following formulae according to their physical properties,
In the above equation,es = ▽ denotes the solid volumetric strain (
denotes the solid volumetric strain ( is the displacement
vector of the solid phase) and
is the displacement
vector of the solid phase) and  = ▽×
= ▽× denotes the rotational strain. The parameters A1
and A2 are obtained as follows[4]:
denotes the rotational strain. The parameters A1
and A2 are obtained as follows[4]:
Solving (1) gives two elastic longitudinal waves which are propagating in the porous material. The corresponding wave number of these two elastic waves,namely structure-borne and airborne are obtained as below,respectively,
Moreover,the corresponding wave number of the shear (rotational) wave is obtained as
where ω is the angular frequency with the coefficients of χ,φ,and μ expressing elastic properties of the porous materials. These parameters are thoroughly explained in Ref. [13].In the above equation,δ denotes shear modulus;  11,
11, 22,and
22,and  12 are equivalent mass
parameters which account for the effects of non-uniform relative fluid flow through the pores
as follows[4]:
12 are equivalent mass
parameters which account for the effects of non-uniform relative fluid flow through the pores
as follows[4]:
Assuming the two dimensional problem of wave propagation through a porous material,the potential function of incident plane wave with unit amplitude is written as follows:
where and c1 is the speed of sound in the incident medium,and γ is the angle of incidence.As shown in Fig. 1,six traveling waves (including three incident waves and three reflected waves) are propagating in the porous layer with a finite depth. They have the same trace wave number as these are induced with an oblique incident wave in a finite depth layer of the porous materials. Displacement,stress field of solid,and fluid phases along x and y directions can be obtained considering the wave propagation through the porous material[4,13].
Therefore,displacement components in the solid phase of the porous material are listed as follows:
In addition,the stress components through solid phase are written asMoreover,the displacement fields of fluid phase are written as
Finally,the stress of fluid phase is written as where Here,E and ν are Young’s modulus and Poisson’s ratio of the bulk solid phase,respectively, while A is a first Lam´e constant. The coefficient χ is positive and represents the coupling between the volume change of the solid and that of the fluid[1]. The constant μ relates the fluid stress to the strain. The parameter R is bulk modulus of elasticity for the fluid in the pore and is generally frequency dependent. It partly represents the stiffness of the fluid as well as the energy transmission at the the wall of the pores (further details can be found in Refs. [4, 13]). Six parameters of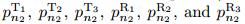 are determined applying the proper
boundary conditions at the interfaces.
3.2 Wave propagation through laminated composite
are determined applying the proper
boundary conditions at the interfaces.
3.2 Wave propagation through laminated composite
As the composite panels play the role of wave propagation media,equations of motion in the laminated composite panels are expressed here. Hereby,the classical laminated plate theory (CLPT) is investigated based on the Kirchhoff Hypothesis[15] as follows:
(i) Straight lines perpendicular to the mid surface (i.e.,transverse normal) before deformation remain straight after deformation.
(ii) The transverse normals do not experience elongation (i.e.,they are inextensible).
(iii) The transverse normals rotate such that they remain perpendicular to the mid surface after deformation.
The first two assumptions imply that the transverse displacement is independent of the transverse (or thickness) coordinates. On the other hand,the transverse normal strain εyy is zero. The third assumption results in zero transverse shear strains γxy = γzy = 0.
Displacement relations based on the theory are followed as[15]:
where (U0,V0,W0) denote displacement along the coordinate lines of a material point on xzplane (x and z represent longitudinal and lateral axes in the composite plate,respectively). From the strain equations of displacement,it can be written asSubstituting (24) into (25) yields
where (ε(0)) is membrane strain,and (ε(1)) is flexural (bending) strain[15].The resultants of force and moment are obtained by integrating the laminated cross section as
The stress-strain relationship in a lamina can be written as
In the above equation,the tensor 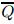 is the plane stiffness tensor of a general orthotropic composite
material in coordinate axis of the panel the elements of which can be found in Ref. [15].
Substitution of (29) into (27)-(28) according to the CLPT,gives the in-plane resultants of force
and moment as follows:
is the plane stiffness tensor of a general orthotropic composite
material in coordinate axis of the panel the elements of which can be found in Ref. [15].
Substitution of (29) into (27)-(28) according to the CLPT,gives the in-plane resultants of force
and moment as follows:
 ij
(k) denotes the planar
stress-reduced stiffness at the kth layer. The equation of motion is found as follows[15]:
where q is the total transfers load. I0 and I1 are the mass moments of inertia calculated as
where ρ(k) is the density of the plate material at kth layer.
3.3 Equilibrium of media interfaces
ij
(k) denotes the planar
stress-reduced stiffness at the kth layer. The equation of motion is found as follows[15]:
where q is the total transfers load. I0 and I1 are the mass moments of inertia calculated as
where ρ(k) is the density of the plate material at kth layer.
3.3 Equilibrium of media interfaces
As depicted in Fig. 2,the porous layer is constrained by a laminated composite plate and an air gap.
 |
| Fig. 2 Cross-section of porous layer in vicinity of air gap[4] |
The transverse and in-plane displacements in the neutral axis are given as follows:
When the elastic porous material is bonded directly to a composite panel,four boundary conditions including the interface between porous and composite layers,and two other boundary conditions according to (34) in the CLPT are obtained. Generally speaking,there are six boundary conditions that must be satisfied: one normal velocity condition,two normal displacement conditions,one tangential surface displacement condition,one center-line in-plane acceleration condition,and one force condition (i.e.,the equation of motion for the panel). According to (37)-(38),these six conditions (in y = 0) are listed as follows[4]:
The first three conditions listed above simply require that normal component of the exterior acoustic particle displacement,transverse displacement of the panel,and normal components of the fluid,and solid displacements in the porous material are all equal. The fourth condition needs that the in-plane surface displacement of a panel vibrating in flexure must be equal to the tangential displacement of the solid phase of the porous material. The fifth condition relates the shear force per unit area applied to the panel to the center-line in-plane acceleration of the plane. The last boundary condition is Euler-Bernoulli equation of the panel but with provisions made for a distributed excitation of moment due to the shear forces acting in the plane of the surface[4].
The following four boundary conditions at the interface of porous layer and air gap must be satisfied: two normal stress conditions,one normal volume velocity condition and one shear stress condition. These conditions (in y = hfoam) are introduced as follows:
The first of these conditions entails that the force per unit area acting on the fluid component of the porous material should be equal to the porosity multiplied by the pressure in the exterior acoustic field. The second equation expresses a similar relation for the force acting on the solid phase. The third condition considers continuity of the normal volume velocity. The final condition states that there is no shear force acting at the free solid surface owing to assumption of an in-viscid exterior fluid[4].
In addition,three equations at the interface of composite layer and air gap (in y = hfoam + hgap) are concluded as
The first two conditions shown above require that the normal acoustic particle velocities at the two faces of the panel are the same as the panel transverse velocity. The last boundary condition of the panel is the equation of Euler-Bernoulli[4]. Here,
In the above-mentioned equations,hp is thickness of the panel,hgap is thickness of the air gap,I0(i) and I1(i) are the mass moments of inertia in the ith layer. A11(i) represents extensional stiffness,B11(i) represents bending-extensional coupling stiffness,D11(i) denotes bending stiffness, p denotes pressure in the exterior acoustics field at the interface,and Vy stands for normal component of the particle velocity in the exterior medium at the interface. 3.4 Vibration equations of structural acoustic
As depicted previously in Fig. 1,14 types of wave branches are propagating into the structure including two incident and reflected waves (pn1i,pn1R),three waves in the composite plates (transverse and shear waves for the first plate (Wp10 ,Wt10) and one shear wave for the second one (Wt20)),three branches of transmitted as well as three reflected waves in the porous material (pn2T1,pn2T2,pn2T3,pn2R1,pn2R2,and pn2R3),transmitted and reflected waves in the air gap (pn3T,pn3R),and finally a transmitted wave into the medium 4 (pn4T) as assumed to be an anechoic environment. Therefore,by considering (39)-(51) a set of equations is constructed as a matrix form,
( ) is a 13 × 13 coefficient matrix,(H) is a vector representing the acoustic forces,and (λ)
is a vector showing the unknown parameters including pressure and displacement fields of the
structure (the elements of matrix (
) is a 13 × 13 coefficient matrix,(H) is a vector representing the acoustic forces,and (λ)
is a vector showing the unknown parameters including pressure and displacement fields of the
structure (the elements of matrix ( ) and vector (H) are listed in Appendix A).
) and vector (H) are listed in Appendix A).
All these equations are solved with respect to amplitude and angle of the incident wave (pn1i,γ). Noting that the TL is independent of the incident wave,its amplitude is assumed to be unit. 3.5 Calculations of TL structure
In practical applications,the incident wave impinges the structure randomly. Therefore,the practical parameter should be introduced to evaluate the experimental results. According to the Paris formula,the averaged pressure transmission coefficient,τ,is calculated as follows[16]:
This parameter will remove the angular dependency of sound transmission through the structure. In (57),τ(γ) is the power transmission proportional to the square of pn4T/pn1i,while γm is the maximum incident angle,usually chosen between 70° and 85°[17]. Integration of (57) is conducted numerically by Simpson’s rule and the average TL is finally obtained as follows:
4 SEAmethodThe work presented in this paper includes a problem in broad band frequencies. Meanwhile, the finite element method (FEM) and boundary element method (BEM) are not sufficiently accurate in high frequency ranges[18]. Therefore,the SEA method is presented to validate the analytical model. For this purpose,a double composite panel with a middle porous layer and air gap is made with the aid of a code developed in AutoSEA2. In this regard,the system includes three subsystems: the first one is the source room,the second one is the double composite panel described above,and the third one is the receiver room. It should be noted that the external excitation was generated by the diffuse source field located in the source room.
Figure 3 depicts power flow transmission through the three subsystems described above. The source and receiver rooms are specified according to ASTM E90. Thus,the source chamber is assumed to be reverberant,while the receiver chamber is deemed anechoic. Dimensions of the panel in comparison with its thickness are significantly large enough to be theoretically infinite.
 |
| Fig. 3 SEA model of composite panel structure with double medium layer of porous and air gap as well as flow of power between three sub-systems |
As shown in Fig. 1,the structural model of the SEA subsystems can be expressed as follows:
(i) The resource room is considered as a reverberant room with damping loss factor of 0.1%.
(ii) The excited composite panel of 1.25 mm thickness with three layers noise control treatment (NCT) forms the double walls. The NCT which is applied to the composite panel involves three below layers:
(a) A layer of porous material with a thickness of 20 mm.
(b) An air gap with a thickness of 10 mm.
(c) A composite panel with a thickness of 1.25 mm,as radiating panel.
(iii) The receiver room is assumed as a quite anechoic room.
A plane connection is considered to properly join the panel surface with both the source and receiver interfaces. According to ASTM E90,the external excitation is generated with a diffusive source located in the source room.
In general,the governing equations of steady state power balance through three subsystems can be written as follows[19]:
In this equation,Πiin is the power input to the ith subsystem,Πidiss is the power dissipated in the ith subsystem,and Πij is the power flow from subsystem (i) to subsystem (j),
where ω is a mid frequency of the frequency band,ηi is a damping loss factor,and ηij is a coupling loss factor from subsystem (i) to subsystem (j)[19].In the source room,the sound power incident (Πinc) on the dividing partition of area Ap is[20,21],
where <P12> stands for the average square sound pressure,c* is the velocity within the cavity, and ρ* is the surface density.The power flow equation for each subsystem is considered. Then,the set of equations are solved simultaneously. Finally,the TL calculated in broad band frequencies is obtained as
5 Results,comparisons,and discussion 5.1 Study on parameters of SEASEA model is considered to be reliable while the numbers of the modes become high as well as the subsystems are poorly coupled. On the other hand,the coupling loss factors of the subsystems should be less than the corresponding damping loss factors. Therefore,in this section,the corresponding parameters are discussed to verify the SEA model. 5.1.1 Modal density
Figure 4 shows the number of modes in a band for all the three subsystems. It can be seen that at high frequencies the number of modes is higher. This happened more rapidly in both cavities rather than the panel. This is the domain of SEA,because the SEA requires a sufficiently high modal density.
 |
| Fig. 4 Number of modes in band for three subsystems |
Figure 5 illustrates the comparison between damping loss factors and coupling loss factors among all the subsystems of the SEA model. It can be clearly observed that the coupling loss factors are smaller than the damping loss factors,especially in high frequency ranges. In other words,the subsystems are weakly coupled.
 |
| Fig. 5 Comparison between damping loss factors and coupling loss factors among all SEA model subsystems |
In order to validate the SEA model,the corresponding results of TL are calculated and compared with those of the presented analytical model and also those reported in an experimental setup[4]. As the experimental results are only available for isotropic (Aluminum) panels,the analytical and SEA codes are thus specified in a special case where the plies are arranged in a [0°,0°,0°,0°,0°]s pattern. As illustrated in Fig. 6,the results reveal the reliability of the SEA and analytical model.
 |
| Fig. 6 Comparing analytical,experimental, and SEA model for isotropic panel |
In order to study accuracy of the solution for a double-walled composite panel with intermediate porous layer,a comparison is made between SEA and analytical solutions. In this case,the panels are assumed to be graphite epoxy and the plies are arranged in a [0°,90°,45°,−45°,0°]s pattern. As depicted in Fig. 7,the two above-mentioned models are properly in agreement with the broad band frequency.
 |
| Fig. 7 Comparison of SEA and analytical model for double-wall composite panel |
In order to study the effects of insulating treatments such as using a porous layer as well as the air gap geometry,a panel composed of ten layers of graphite-epoxy (including the porous layer and air gap) is considered. In addition,two similar structures are chosen including a singlewall composite with and without foam layer. The physical specifications of these constructions are listed in Table 2,while the corresponding results are illustrated in Fig. 8. As can be seen, the power of double-panel insulation is significant in comparison with the two other similar panels,especially in high frequency ranges.
 |
| Fig. 8 Comparison of effects of foam layer and air gap on sound transmission through panel |
The geometrical and mechanical parameters of the porous layer and composite panels on structural TL are investigated here. Therefore,all the engaged parameters are divided into the following two categories:
(i) Parameters associated with a porous layer which mainly contains the fluid phase of the porous layer (porosity,tortuosity,and flow resistivity) and also the solid phase of the porous layer (bulk density,bulk Young’s modulus,and Poisson’s ratio).
(ii) Parameters associated with composite panels including wall thickness of the composite material. 5.3.1 Specifications of porous layer
The main target for improving acoustical behavior of the porous layer is to increase its thickness. Figure 9 shows effects of the porous thickness on sound transmission of the composite panel. As the thickness of the porous layer increases,it is well anticipated that the TL will be increased. Discrepancy of the curves will be more significant in high frequency ranges as a result of shortening of the wave length. In contrast,the coincidence frequency will be decreased with increasing of the porous thickness.
 |
| Fig. 9 Effect of porous layer thickness on TL |
An alternative approach to improve the acoustical behavior of a sound insulated structure is associated with fluid phase of the porous material,such as porosity,flow resistivity,and tortuosity. The effects of these parameters on power transmission are investigated through Figs. 10-12.
 |
| Fig. 10 Effects of porosity of porous layer on TL |
 |
| Fig. 11 Effects of flow resistivity of porous layer on TL |
 |
| Fig. 12 Effects of tortuosity on TL |
The results indicate that,the fluid phase of the porous material is particularly effective in high frequency ranges. It is also shown that,increasing of the porosity and flow resistivity will slightly enhance the TL. On the other hand,the power transmission is significantly reduced with increasing the tortuosity.
Moreover,the influence of corresponding parameters of the solid phase of the porous layer such as bulk density,bulk Young’s modulus,and Poisson’s ratio on TL of the composite panel is depicted in Figs. 13-15. Similar to the fact mentioned before,these parameters are particularly effective in high frequency ranges.
 |
| Fig. 13 Comparison of TL of structure with porous material with different bulk densities |
 |
| Fig. 14 Comparison of TL of structure with porous material with different bulk Young’s moduli |
 |
| Fig. 15 Comparison of TL of structure with porous material with different Poisson’s ratios |
Figure 13 shows that the bulk density of the porous layer in broad band frequency behaves in a different way. In low frequencies increasing the bulk density will improve the TL. However, in high frequencies it significantly reduces the TL.
As shown in Fig. 14,improving the structural rigidity increases the TL of the structure in high frequency ranges significantly as a result of growth in the bulk Young’s modulus of the porous layer.
The effects of Poisson’s ratio of porous layer on sound transmission through the structure are depicted in Fig. 15. In spite of the fact that Poisson’s ratio has no effect in lower frequencies, the power transmission will be improved by increasing the Poisson’s ratio in high frequencies.
It should be noted that the parameters described above can be effective regarding the boundary conditions of the structures. In other words,these parameters are related to how the acoustic energy is transmitted through air-borne or structure-borne waves. 5.3.2 Parameters of composite panels
One of the important parameters in noise transfer is thickness of the panels. Therefore, according to Fig. 16,the thickness effect of the composite panels on TL is examined. As can be observed from this figure,increasing thickness of the composite panels improves the TL of the structure in broad band frequencies.
 |
| Fig. 16 Effect of thickness of composite panels on TL |
The effect of composite material is shown in Fig. 17. These material specifications are listed in Table 2. As depicted in this figure,the composite made of glass-epoxy shows that the TL improves more than other materials as a result of its larger density.
 |
| Fig. 17 Effect of composite material on TL |
Figure 18 shows the effect of arrangement of the composite plies on TL. Three types of arrangement are considered as [0°,90°,45°,−45°,0°]s,[0°,0°,0°,0°,0°]s,and [90°,90°,90°, 90°,90°]s. As shown,arrangement of the plies could affect the structural TL in high frequency.
 |
| Fig. 18 Effect of composite plies arrangement in TL |
In this paper,the governing equations of porous layer are described based on the Biot theory. In addition,the viscous and inertia terms are considered to be coupled. Moreover,the stressstrain equations are derived by the thermal and elastic couplings. Then,the analytical model for sound transmission through a double-walled laminated composite is presented. The structure is excited by plane waves,while the SEA is employed to simulate the problem. Then,analytical results are compared with those obtained from the SEA. The comparison shows reliability of the model. The results mainly indicate that the present double-walled structure would improve the power transmission as well as the weight reduction,especially in high frequency ranges. Moreover,it can be inferred from the results that in the case of bounded-unbounded,where the porous layer is located between the panel and the air gap,a major part of the wave energy is transmitted through the structure-borne wave,whereas the remaining is transmitted through the air-borne wave. Therefore,the effects of those parameters associated with the solid phase of the porous layer are of high importance. At the end,it can be concluded that the composite material along with layer stacking sequence of the composite plies is more effective on TL, especially in high frequency ranges. Appendix A
The non-zero components of the matrix ( ) appearing in (56) are as follows:
) appearing in (56) are as follows:

H matrix elements include

Assume that

where

| [1] | Biot, M. A. Theory of propagation of elastic waves in a fluid-structural porous solid I: low frequencyrange. The Journal of the Acoustical Society of America, 28(2), 168-178 (1956) |
| [2] | Bolton, J. S. and Green, E. R. Normal incidence sound transmission through double-panel systemslined with relatively stiff, reticulated polyurethane foam. Applied Acoustics, 39(1), 23-51 (1993) |
| [3] | Bolton, J. S., Heng, Y. L., Katragadda, S., and Alexander, J. H. Layered fibrous treatment for asound absorption and transmission control. SAE 971878, 2576-2590 (1997) |
| [4] | Bolton, J. S., Shiau, N. M., and Kang, Y. J. Sound transmission through multi-panel structureslined with elastic porous materials. Journal of Sound and Vibration, 191(3), 317-347 (1996) |
| [5] | Allard, J. F. and Atalla, N. Propagation of Sound in Porous Media: Modeling Sound AbsorbingMaterials, Elsevier Applied Science, New York (2009) |
| [6] | Cimerman, B., Bremner, P., Yang, Q., and van Buskirk, J. A. Incorporating layered acoustic trimmaterials in body structural-acoustic models. SAE 951307, 2289-2294 (1995) |
| [7] | Zeng, X., Woo, J., and Tang, H. The effects of laminated steel body panels on vehicle interiornoise. Proceedings of the Second International Auto SEA Users Conference, Michigan, U. S.A.(2002) |
| [8] | Tadeu, A., Antonio, J., and Mateus, D. Sound insulation provided by single and double panelwalls鈥攁 comparison of analytical solutions versus experimental results. Applied Acoustics, 65(1),15-29 (2004) |
| [9] | Onsay, T. Use of SEA in a car program. SAE Noise and Vibration Conference, U. S.A. (2007) |
| [10] | Ghosh, A. K., Williams, A. D., Zucker, J. M., Mathews, J. L., and Spinhirne, N. An experimentalinvestigation into the acoustic characteristics of fluid-filled porous structures鈥攁 simplified modelof the human skull cancellous structure. Experimental mechanics, 48(2), 139-152 (2008) |
| [11] | Xin, F., Lu, T., and Chen, C. Vibroacoustic behavior of clamp mounted double-panel partitionwith enclosure air cavity. The Journal of the Acoustical Society of America, 124(6), 3604-3612(2008) |
| [12] | Xin, F. and Lu, T. Transmission loss of orthogonally rib-stiffened double-panel structures withcavity absorption. The Journal of the Acoustical Society of America, 129(4), 1919-1934 (2011) |
| [13] | Daneshjou, K., Ramezani, H., and Talebitooti, R.Wave transmission through laminated compositedouble-walled cylindrical shell lined with porous materials. Appl. Math. Mech. -Engl. Ed., 32(6),701-718 (2011) DOI 10.1007/s10483-011-1450-9 |
| [14] | Lee, J. H. and Kim, J. Simplified method to solve sound transmission through structures linedwith elastic porous material. The Journal of the Acoustical Society of America, 110(5), 2282-2294(2001) |
| [15] | Reddy, J. N. Mechanics of Laminated Composite Plates and Shells: Theory and Analysis, CRCPress, Boca Raton (2004) |
| [16] | Pierce, A. D. Acoustics, McGraw Hill, New York (1981) |
| [17] | Mulholland, K. A., Parbrook, H. D., and Cummings, A. The transmission loss of double panels.Journal of Sound and Vibration, 6(3), 324-334 (1967) |
| [18] | ESI Group. AutoSEA2 User's Guide, Vibro-Acoustic Sciences, San Diego (2004) |
| [19] | Craik, R. J. M. Non-resonant sound transmission through double walls using statistical energyanalysis. Applied Acoustics, 64(3), 325-341 (2003) |
| [20] | Moore, J. A. and Lyon, R. H. Sound transmission loss characteristics of finite sandwich panelconstructions. The Journal of Acoustic Society of America, 89(2), 777-791 (1991) |
| [21] | Cremer, L., Heckl, M., and Ungar, E. Structure-Borne Sound, Springer Verlag, Berlin (1988) |
 2014, Vol. 35
2014, Vol. 35







































