Shanghai University
Article Information
- He ZHANG, Ji-qing JIANG, Zhi-cheng ZHANG. 2014.
- Three-dimensional elasticity solutions for bending of generally supported thick functionally graded plates
- Appl. Math. Mech. -Engl. Ed., 35(11): 1467-1478
- http://dx.doi.org/10.1007/s10483-014-1871-7
Article History
- Received 2013-11-29;
- in final form 2014-4-30
2. School of Civil Engineering, Zhejiang University City College, Hangzhou 310058, P.R. China;
3. Department of Civil Engineering, Zhejiang University, Hangzhou 310058, P.R. China
Functionally graded material (FGM) is a new generation of composites which was proposed by materials scientists in the early 1980s and used in thermal barriers [1] . FGM is tailored commonly by controlling the volume fractions,microstructure,porosity,etc. of the material constituents during manufacturing,thus resulting in spatial gradient of macroscopic material properties,such as mass density,Young’s modulus,Poisson’s ratio,mechanical strength,and thermal conductivity. This makes FGMs possess various advantages over conventional laminate composites in mechanical behavior including thermal stresses,stress concentrations,intensity factors,or attenuation of stress waves,etc. As a result,FGMs have seen wide applications in modern engineering and attracted intensive research focus during the past decades.
As extended applications,various two-dimensional (2D) plate theories have been used to investigate the static bending of functionally graded plates in the past years,such as the thin plate theory with Kirchhoff hypothesis [2] ,the first-order shear deformation theory [3,4] ,the thirdorder plate theories [5,6,7] ,and the refined higher-order theories [8,9,10] . Due to the hypotheses and simplification concerning the deformation field along the thickness direction,the applicability of the 2D plate theories is always confined to the plates with lower thickness-to-length ratios. To account for the deformation field as complete as possible,three-dimensional (3D) elasticity solutions were widely exploited for FGM plates [11,12,13,14,15,16,17,18,19,20] . Since the spatial variation of material properties,it is rather difficult to derive analytical solutions for FGM plate based on the 3D elasticity theory. The common treatment was to assumez-dependent material properties and dealt with the through-thickness and in-plane direction separately. For example,the series expansions were used to derive an asymptotic solution in the thickness direction [11,12,13] ,while the exponential law was also widely used to describe the variation of stiffness constants in the thickness direction and thus decouple thez-dependence from the governing equation [14,15,16,17,18] .The former encounters a large number of recurrence manipulations which causes low efficiency of calculation,while the synchronous exponential-law variations of all material properties are no more than the theoretical meaning. To consider FGM plates with arbitrarily varying material properties through the thickness,Chen et al. [19] combined the approximate laminate model (ALM) and the state space method to obtain an asymptotic solution. It is noted that the above exact or asymptotic solutions [11,12,13,14,15,16,17,18,19] were all for fully simply supported plates by expanding all physical quantities into double Fourier series in both in-plane directions. For plates with nonsimple supports,say clamped or free edges,the general solution cannot be expanded into Fourier series. Hence,analyticalsolutions are impossible. Recently,Vaghefi et al. [20] used the meshless local Petrov-Galerkin (MLPG) method to derive a 3D elasticity solution for bending of generally supported FGM plates. However,their solutionis restricted to exponential law variations of Young’s modulus. In addition,the performing of MLPG in both three directions makes the size of the final equation very large and hence high computational cost.
For the purpose of treating generally supported plates with high computational efficiency, the semi-analytical solution may be an alternative. Fortunately,the state space method (SSM) was successfully combined with the generalized differential quadrature method (DQM),the so-called state-space based differential quadrature method (SSDQM),by Chen and his coworkers [21,22,23,24,25] for laminated beams and plates,functionally graded beams,and continuously multi-span plates,etc. In this paper,the SSDQM is used to obtain the semi-analytical threedimensional elasticity solutions for generally supported functionally graded thick plates. The volume fraction of each constituent phase is assumed to vary through the thickness according to a power-law function,and the material properties are determined by the micromechanicsbased Mori-Tanaka model [26] . The DQM is used to approximate the variables along the in-plane direction,while the thickness domain of the plates is solved asymptotically using the ALM [19,27] combined with on the SSM. Convergence studiesare performed to examine the effectiveness of both SSDQM and ALM by comparing the present results to exact solutions for plates with exponential law variations. Numerical examples are performed to investigate the effects of gradient index and aspect rations on the stress distributions in thick plates with non-fully simple supports. 2 State space formulations For an orthotropic FGM plate,with the lengtha,widthb,and uniform thickness h,the coordinate system (x,y,z) is established with the origin coincident with one corner of the place,which gives 0≤x≤a,0≤y≤b,and 0≤z≤h. In the absence of body forces,the strain-displacement relation,and equations of equilibrium are
where σi and τij (i,j =x,y,z) are the normal and shear stress components,respectively,cij are the elastic stiffness constants which vary continuously and smoothly through the thickness direction,i.e.,cij≡cij(z).Combining (1) and (2) and performing the routine derivation of SSM [19] lead to the following state equation:
where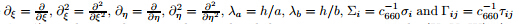 (i,j=ξ,η,ζ) are the non-dimensional normal and shear stresses,respectively,(U,V,W)=(u,
v,w)/hare the non-dimensional displacement components,ξ=x/a,η=y/b,and ζ=z/h are
the non-dimensional coordinates,and c660 is the elastic constant at the surface of ζ=0. The
coefficients Ci are determined by the elastic stiffness constants cij as
In the state equation (3),all variables are termed the state variables,by virtue of which the
induced variables are expressed as
(i,j=ξ,η,ζ) are the non-dimensional normal and shear stresses,respectively,(U,V,W)=(u,
v,w)/hare the non-dimensional displacement components,ξ=x/a,η=y/b,and ζ=z/h are
the non-dimensional coordinates,and c660 is the elastic constant at the surface of ζ=0. The
coefficients Ci are determined by the elastic stiffness constants cij as
In the state equation (3),all variables are termed the state variables,by virtue of which the
induced variables are expressed as
Generally,it is difficult to obtain an analytical solution of the partial differential equation (3) for a plate with arbitrary boundary conditions. As for general supports,numerical techniques are required. Here,we exploit the DQM [22] to approximate the derivatives aboutξandηon the right side of (3). Hence,a system of ordinary differential state equation at an arbitrary discrete point (ξi,gηj) is obtained as
where X(n)ij and Y(n)ij are the weighting coefficients for thenth-order derivative about ξ and η,respectively. In addition,the coefficients X(n)ij (or Y(n)ij) are uniquely determined according to the number Nx(or Ny)andthecoordinates ξi (or ηj) of the sampling discrete points[22] . Accordingly,the induced variables at all discrete points are obtained as By virtue of the discrete variables,the boundary conditions at four edges are expressed as simple supported edge (S) : for ξ=0 (i=1) orξ=1 (i=Nx); and for η=0 (j=1) or η=1 (j=Ny).In order to obtain the unique solution to (6),the boundary conditions in (8) and (9) should be incorporated. In detail,all boundary conditions should be rearranged in terms of the state variables,i.e.,the state variables at four edges are either zero or algebraically related to other state variables unknown with respect to ζ. Therefore,the differential equations of the state variables at the edges should be eliminated [20] . Upon incorporating all boundary conditions, the state equation (6) is further reduced to
where δ and M are respectively the new global state vector and coefficient matrix obtained according to the boundary conditions in (8) and (9). 3 Solutions with ALM
As mentioned at the very beginning,material constants vary continuously through the thickness direction,due to which (10) is a differential equation with variant coefficient matrix and
is rather difficult to solve directly. Here,the ALM
[15]
is employed,in which the plate is divided
into partificial layers,each with a small thicknesshk. Each layer is thin enough so that it can
be regarded as homogeneous to have constant material properties which are the same as that
at the mid-plane, Based on this approximation,the state equation
with constant coefficient matrix for thekth layer is obtained as
Based on this approximation,the state equation
with constant coefficient matrix for thekth layer is obtained as
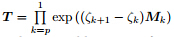 is the global transfer matrix,and the subscripts ‘t’ and ‘b’
indicate the top and bottom surfaces,respectively. Upon introducing the traction conditions at
the two lateral surfaces in (13),the displacement vectors at the bottom surface can be solved.
For the present bending problem,the plate is assumed subjected to normal loads Σζ,t and Σζ,b
at the two surfaces. Therefore,the solution is
where tij are the blocked matrices of the transfer matrix T. Once the displacement vectors
at the surface ζ = 0 are obtained,repeated performing of (12) together with the continuity
conditions will yield the state vectors at an arbitrary coordinateζ. Note that the boundary
conditions at the two lateral surfaces are notnecessarily limited to the normal traction but
arbitrary with both normal and shear tractions.
is the global transfer matrix,and the subscripts ‘t’ and ‘b’
indicate the top and bottom surfaces,respectively. Upon introducing the traction conditions at
the two lateral surfaces in (13),the displacement vectors at the bottom surface can be solved.
For the present bending problem,the plate is assumed subjected to normal loads Σζ,t and Σζ,b
at the two surfaces. Therefore,the solution is
where tij are the blocked matrices of the transfer matrix T. Once the displacement vectors
at the surface ζ = 0 are obtained,repeated performing of (12) together with the continuity
conditions will yield the state vectors at an arbitrary coordinateζ. Note that the boundary
conditions at the two lateral surfaces are notnecessarily limited to the normal traction but
arbitrary with both normal and shear tractions.
It should be pointed out that the numerical difficulties would be encountered if the plate is thick. In detail,numerical instabilities will occur when performing the inverse manipulation of the matrix in (14) if the plate is in thick configurations. This problem was well clarified and successfully removed by L¨ uetal.[23] when treating continuous plates and generally supported thick laminated plates [25] . In the current work,we will also use the combined transfer matrix method and the joint coupling matrix proposed in [23] to obtain numerical results with satisfying accuracy for thick plates. 4 Numerical examples 4.1 Validation analysis
To examine the effectiveness of both SSDQM and ALM,the convergence study is performed first. Here,for representative illustration,we consider an SSSS supported FGM plate with the Young’s modulus varying exponentially through thickness,i.e.,E(z)=E0eαz/h,where α=ln(Eh/E0) is the gradient index,and E0 and Eh are Young’s moduli at the bottom and top surfaces,respectively. For this problem,we can derive a strictly exact solution using the SSM with double Fourier series expansions,which is similar to that for elastic FGM plates on elastic foundations [15] .
For the implementation of the differential quadrature procedure,the unequally spaced sampling points in cosine pattern [28] are exploited in this paper. The relative error of the present SSDQM solutionδagainst the exact solution δ0 is defined as (δ−δ0)/δ0×100%,where δ denotes a certain variable. Taking an SSSS FGM plate with h/a=0.2,Eh/E0=0.5 and applied uniform load at the lower surface for example,the decaying of this relative error for the maximal transverse displacementwmaxand in-plane normal stressσx,b(0.5a,0.5b,0) versus the number of artificial layers using various discrete sampling points in thex-andy-directions are plotted in Fig. 1. It is confidence that the choosing 30 layers in the ALM and 9×9 discrete points for the in-plane domain will deliver sufficiently accurate results.
 |
| Fig. 1 Convergence study of present SSDQM and ALM for SSSS FGM square plate (h/a=0.2and Eh/E0=0.5) |
To further validate the effectiveness of SSDQM,the transverse displacement and in-plane normal stress for FGM square plates (h/a=0.3) with various boundary conditions and various Eh/E0 are computed using 30 layers in the ALM and 9×9 discrete points and presented in Table 1,where the exact solutions [15] for SSSS plate,3D MLPG,and finite element method (FEM) results [20] for all plates are also listed. Apparently,the present results coincide very well with these 3D solutions. Hence,the effectiveness of SSDQM with 9×9 discrete points and the ALM with 30 layers for generally supported FGM plates is also validated.
There have been proposed various methods to determine the locally effective material properties including the exponential law,power law,and micromechanical models,etc. The exponential or power law functions are often able to facilitate analytical solutions for FGM structures. In contrast,micromechanical models,such as Mori-Tanaka [26] ,self-consistent [29] ,and Viogt model (rule of mixture)[30] are the widely acceptable models forpredicting the locally effective elastic moduli of FGM since they account for the interactions between constituent phases based on solving the average local stress and strain fields. It has been reported that the Voigt and Mori-Tanaka models have the same accuracy in predicting the buckling and vibration characteristics of functionally graded ceramic-metal beams,plates,and shells [31,32,33,34] . Here,we consider an FGM plate composed of two-phase composite reinforced by spherical particles in the plate plane,and the effective material properties are predicted by the Mori-Tanaka model [26] ,in which the effective bulk modulusKe and the effective shear modulusμe are given by
whereK,μ,and V(z) are the bulk modulus,shear modulus,and volume fraction of individual material constituent,and the subscripts “1” and “2” denote two different material phases. The bulk and shear moduli of the material are determined by Young’s modulusEand Poisson’s ratio ν as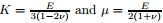 .
.
Here,we assume that the FGM plate is made of an aluminum alloy (Al) for metal phase and zirconia (ZrO2 ) for ceramic phase. The corresponding materials are respectively Em=70 GPa and νm=0.3 for Al[8] ,and Ec=168.06 GPa and νc=0.3 for ZrO2[35]. The volume fraction of ZrO2 is given by the power law V2=(z/h)α ,whereαis the gradient index indicating the variation through the thickness. This scheme of volume fraction indicates that the bottom surface is pure Al and the top pure ZrO2 . Figure 2 exhibits the through-thickness variation of the normalized effective Young’s moduliEe/Emof the Al/ZrO2 plate. It is obvious that when the gradient index is very small (e.g.,α=0.2) or very large (e.g.,α=5),the effective Young’s modulus varies drastically within the metal-rich or ceramic-rich area.
 |
| Fig. 2 Through-thickness variation of normalized effective Young’s moduli of Al/ZrO2 plate for various gradient indexα(insert shows schematic spatial distribution of Al and ZrO2 phases along thickness direction) |
Generally supported FGM square plate (a=b) subjected to a uniform pressure q0 on the ZrO2 surface is considered in this section. The deflectionw,the in-plane normal stress σx,and the shear stress τxy are normalized as
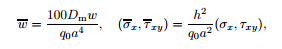
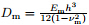 is the bending rigidity of an aluminum plate.
is the bending rigidity of an aluminum plate.
Firstly,the effectiveness of the SSDQM for FGM plates with Mori-Tanaka type material
properties and various boundary conditions is studied. To compare the current results with the
HOPT[8] solutions,the Young’s modulus for ZrO2 in this example is taken as Ec= 200 GPa.
Figures 3-5 exhibit the numerical results for through-thickness distributions of normalized deflection  and in-plane normal stress
and in-plane normal stress  x of SSSS,SCSC,and CCCC square plates with h/a=0.2
and gradient index α=1 and α=2. In the figures,the solid square markers denote the HOPT
results
[8]
obtained using the MLPG method based on the higher-order shear and normal deformable plate theory. It is seen that the present results agree well with the HOPT results. It
is also shown that the larger the gradient index is,the smaller deflection is of the plate. This is
mainly due to the fact that the volume fraction of ZrO2 with larger Young’s modulus increases
with the gradient index α.
x of SSSS,SCSC,and CCCC square plates with h/a=0.2
and gradient index α=1 and α=2. In the figures,the solid square markers denote the HOPT
results
[8]
obtained using the MLPG method based on the higher-order shear and normal deformable plate theory. It is seen that the present results agree well with the HOPT results. It
is also shown that the larger the gradient index is,the smaller deflection is of the plate. This is
mainly due to the fact that the volume fraction of ZrO2 with larger Young’s modulus increases
with the gradient index α.
 |
| Fig. 3 Through-thickness distributions of non-dimensional transverse displacement and in-plane normal stress of SSSS square at x=a/2 and y=b/2 (h/a=0.2) |
 |
| Fig. 4 Through-thickness distributions of non-dimensional transverse displacement and in-plane normal stress of SCSC square at x=a/2 and y=b/2 (h/a=0.2) |
Next,the effects of gradient index on the stress distributions of FGM plates are studied.
In practical applications,the gradient indexαshould not be too small or too large,otherwise,
the tailored FGM will contain too much of one constituent phase and too little of the other.
Nakamura et al.[36]
suggested 1/3<α<3 so that the volume fraction of each constituent phase
takes 25%-75%. Here,we consider a metal rich FGM plate with α=1,2,or5forrepresentatively
theoretical illustrations. Figure 6 plots the through-thickness distributions of the in-plane
normal stress  x and in-plane shear stress
x and in-plane shear stress  xy of a CCCC square plate (h/a=0.2) for various
α. It is observed that the nonlinear distributions of
xy of a CCCC square plate (h/a=0.2) for various
α. It is observed that the nonlinear distributions of  x and
x and  xy become increasingly obvious
asαincreases. The fibers at the vicinity of Al rich surface bear an increasing tensile stress
as the volume fraction of ZrO2 becomes increases. Similar trends are also observed for the
compressive stress near the ZrO2 rich surface,and the in-planeshear stress at the vicinity of
the two surfaces.
xy become increasingly obvious
asαincreases. The fibers at the vicinity of Al rich surface bear an increasing tensile stress
as the volume fraction of ZrO2 becomes increases. Similar trends are also observed for the
compressive stress near the ZrO2 rich surface,and the in-planeshear stress at the vicinity of
the two surfaces.
 |
| Fig. 5 Through-thickness distributions of nondimensional transverse displacement and in-plane normal stress of CCCC square at x=a/2 and y=b/2 (h/a=0.2) |
 |
| Fig. 6 Effects of gradient indexαon through-thickness distributions of in-plane normal and shear stresses of CCCC plates (h/a=0.2) |
Finally,to investigate the effects of aspect ratio h/a on the stress distributions in FGM plates,we consider the SCSC and CCCC plates with α= 3 as illustrative examples. The through-thickness distributions of in-plane normal stress σx and shear stress τxy for various aspect ratio h/a are shown in Figs. 7 and 8. It is seen that,for a given gradient index (α=3), the distributions of in-plane normal and shear stresses become increasingly drastic as the plate gets thicker regardless of the boundary conditions. Both Figs. 7 and 8 show that the existence of material gradient will shift the neutral plane. For the case of α=3,the neutral plane moves toward the lower surface,i.e.,the soft phase with rich Al.
 |
| Fig. 7 Effects of aspect ratio h/a on through-thickness distributions of inplane normal and shear stresses of SCSC plate (α=3) |
 |
| Fig. 8 Effects of aspect ratioh/aon throughthickness distributions of in-plane normal and shear stresses of CCCC plate (α=3) |
Bending analysis of FGM thick plates is carried out via the newly developed SSDQM. Directly based on the 3D theory of elasticity,no assumptions of the distributions of displacement and stress are introduced,which enables the current method applicable for plates with arbitrary thickness. The current semi-analytical method has two merits: (i) the introduction of differential quadrature makes it possible to extend the SSM to plates with arbitrary boundary conditions,thus expanding the application of the traditional SSM for FGM plates; (ii) to imple-ment the differential quadrature in the state space formalism avoids forcing some of the inner discrete points to satisfy higher-order boundary conditions,since all boundary conditions are now expressed by stress or displacement components at the edges. That is,physical approximations commonly encountered during performing DQM for higher-order differential equations are avoided. On the other hand,although the Mori-Tanaka method is not appropriate enough to determine the effective material properties for FGM especially at location where the inclusion is rich,the approximate laminate model is universal for arbitrarily through-thickness variations of material properties once the effective properties are predicted precisely.
Numerical results indicate that for two-phase functionally graded plates,the in-plane normal and shear stresses will vary more gently through the thickness direction for rich volume fraction of hard phase. It is also shown that the stress level is lower for thin plates than that for thick plate. In addition,the neutral plane of the plate will shift as the volume fraction of hard phase varies for two-phase functionally grade plate. All these findings may render theoretical references for the design of functionally graded materials for various application purposes in practical engineering.
| [1] | Koizumi, M. FGM activities in Japan. Composites Part B: Engineering, 28(1-2), 1-4 (1997) |
| [2] | Fereidoon, A., Asghardokht, S. M., and Mohyeddin, A. Bending analysis of thin functionallygraded plates using generalized differential quadrature method. Archive of Applied Mechanics,81, 1523-1539 (2011) |
| [3] | Zenkour, A. M. A comprehensive analysis of functionally graded sandwich plates, part 1: deflectionand stresses. International Journal of Solids and Structures, 42(18-19), 5224-5242 (2005) |
| [4] | Nguyen, T. K., Sab, K., and Bonnet, G. First-order shear deformation plate models for functionallygraded materials. Composite Structures, 83(1), 25-36 (2008) |
| [5] | Yang, J. and Sheng, H. S. Nonlinear bending analysis of shear deformable functionally gradedplates subjected to thermo-mechanical loads under various boundary conditions. Composites PartB: Engineering, 34(1), 103-115 (2003) |
| [6] | Reddy, J. N. Analysis of functionally graded plates. International Journal for Numerical Methodsin Engineering, 47(1-3), 663-684 (2000) |
| [7] | Wu, C. P. and Li, H. Y. An RMVT-based third-order shear deformation theory of multilayeredfunctionally graded material plates. Composite Structures, 92(10), 2591-2605 (2010) |
| [8] | Gilhooley, D. F., Batra, R. C., Xiao, J. R., McCarthy, M. A., and Gillespie, J. W. Analysis ofthick functionally graded plates by using higher-order shear and normal deformable plate theoryand MLPG method with radial basis functions. Composite Structures, 80(4), 539-552 (2007) |
| [9] | Matsunaga, H. Free vibration and stability of functionally graded plates according to a 2-D higherorderdeformation theory. Composite Structures, 82(4), 499-512 (2008) |
| [10] | Sahraee, S. and Saidi, A. R. Axisymmetric bending analysis of thick functionally graded circularplates using fourth-order shear deformation theory. European Journal of Mechanics A—Solids,28(5), 974-984 (2009) |
| [11] | Batra, R. C. and Vel, S. S. Exact solution for thermoelastic deformations of functionally gradedthick rectangular plates. AIAA Journal, 40(7), 1421-1433 (2001) |
| [12] | Reddy, J. N. and Cheng, Z. Q. Three-dimensional thermomechanical deformations of functionallygraded rectangular plates. European Journal of Mechanics A—Solids, 20(5), 841-855 (2001) |
| [13] | Wen, P. H., Sladek, J., and Sladek, V. Three-dimensional analysis of functionally graded plates.International Journal for Numerical Methods in Engineering, 87(10), 923-942 (2011) |
| [14] | Kashtalyan, M. Three-dimensional elasticity solution for bending of functionally graded rectangularplates. European Journal of Mechanics A—Solids, 23(5), 853-864 (2004) |
| [15] | Huang, Z. Y., Lü, C. F., and Chen, W. Q. Benchmark solutions for functionally graded thick platesresting on Winkler-Pasternak elastic foundations. Composite Structures, 85(1), 95-104 (2008) |
| [16] | Xu, Y. P. and Zhou, D. Three-dimensional elasticity solution of functionally graded rectangularplates with variable thickness. Composite Structures, 91(1), 56-65 (2009) |
| [17] | Alibeigloo, A. Three-dimensional exact solution for functionally graded rectangular plate withintegrated surface piezoelectric layers resting on elastic foundation. Mechanics of Advanced Materialsand Structures, 17, 183-195 (2010) |
| [18] | Wu, C. P., Chiu, K. H., and Wang, Y. M. RMVT-based meshless collocation and element-freeGalerkin methods for the quasi-3D analysis of multilayered composite and FGM plates. CompositeStructures, 93, 923-943 (2011) |
| [19] | Chen, W. Q., Bian, Z. G., and Ding, H. J. Three-dimensional analysis of a thick FGM rectangularplate in thermal environment. Journal of Zhejiang University Science A, 4(1), 1-7 (2003) |
| [20] | Vaghefi, R., Baradaran, G. H., and Koohkan, H. Three-dimensional static analysis of thick functionallygraded plates by using meshless local Petrov-Galerkin (MLPG) method. EngineeringAnalysis with Boundary Elements, 34, 564-573 (2010) |
| [21] | Chen, W. Q., Lü, C. F., and Bian, Z. G. Elasticity solution for free vibration of laminated beams.Composite Structures, 62(1), 75-82 (2003) |
| [22] | Lü, C. F. State-Space-Based Differential Quadrature Method and Its Applications, Ph. D. dissertation,Zhejiang University (2006) |
| [23] | Lü, C. F., Zhang, Z. C., and Chen, W. Q. Free vibration of generally supported rectangular Kirchhoffplates: state-space-based differential quadrature method. International Journal for NumericalMethods in Engineering, 70(12), 1430-1450 (2007) |
| [24] | Lü, C. F., Chen, W. Q., Xu, R. Q., and Lim, C. W. Semi-analytical elasticity solutions forbi-directional functionally graded beams. International Journal of Solids and Structures, 45(1),258-275 (2008) |
| [25] | Lü, C. F., Chen, W. Q., and Shao, J. W. Semi-analytical three-dimensional elasticity solutions forgenerally laminated composite plates. European Journal of Mechanics A—Solids, 27(5), 899-917(2008) |
| [26] | Mori, T. and Tanaka, K. Average stress in matrix and average elastic energy of materials withmisfitting inclusions. Acta Metallurgica, 21(5), 571-574 (1973) |
| [27] | Chen, W. Q. and Ding, H. J. Bending of functionally graded piezoelectric rectangular plates. ActaMechanica Solida Sinica, 13(4), 312-319 (2000) |
| [28] | Sherbourne, A. N. and Pandey, M. D. Differential quadrature method in the buckling analysis ofbeams and composite plates. Computers and Structures, 40(4), 903-913 (1991) |
| [29] | Hill, R. A self-consistent mechanics of composite materials. Journal of the Mechanics and Physicsof Solids, 13(2), 213-222 (1965) |
| [30] | Voigt, W. Ueber die beziehung zwischen den beiden elasticitätsconstanten isotroper körper. Annalender Physik, 274(12), 573-587 (1889) |
| [31] | Librescu, L., Oh, S. Y., and Song, O. Thin-walled beams made of functionally graded materialsand operating in a high temperature environment: vibration and stability. Journal of ThermalStresses, 28(6-7), 649-712 (2005) |
| [32] | Huang, C. S., McGee, O. G., and Chang, M. J. Vibrations of cracked rectangular FGM thickplates. Composite Structures, 93(7), 1747-1764 (2011) |
| [33] | Shen, H. S. and Wang, Z. X. Assessment of Voigt and Mori-Tanaka models for vibration analysisof functionally graded plates. Composite Structures, 94(7), 2197-2208 (2012) |
| [34] | Shen, H. S. Nonlinear vibration of shear deformable FGM cylindrical shells surrounded by anelastic medium. Composite Structures, 94(3), 1144-1154 (2012) |
| [35] | Shackelford, J. F. and Alexander, W. CRC Materials Science and Engineering Handbook, CRCPress, Boca Raton (2000) |
| [36] | Nakamura, T., Wang, T., and Sampath, S. Determination of properties of graded materials byinverse analysis and instrumented indentation. Acta Materialia, 48(17), 4293-4306 (2000) |
 2014, Vol. 35
2014, Vol. 35

















