Shanghai University
Article Information
- Chao LIU, Xing-nian LIU, Ke-jun YANG. 2014.
- Predictive model for stage-discharge curve in compound channels with vegetated floodplains
- Appl. Math. Mech. -Engl. Ed., 35(12): 1495-1508
- http://dx.doi.org/10.1007/s10483-014-1884-6
Article History
- Received 2013-11-19;
- in final form 2014-4-8
2. State Key Laboratory of Hydraulics and Mountain River Engineering, Sichuan University, Chengdu 610065, P. R. China
The stage-discharge curve is quite important to the hydrological computation and forecast in natural river. It is also crucial for the flood prediction. When flood happens,the flow depth increases significantly and the overbank flow may be observed in the compound channel where the characteristics of the flow discharge are totally different from that of the single channel. For example,the hydraulic radius for a compound channel is abruptly increasing when the flow depth reaches the overbank level. This causes some typical mathematical issues for predicting the stage-discharge curve. To explore the flow characteristics in the compound channel clearly, large numbers of experiments have been conducted in a large-scale compound channel in the U. K. Flood Channel Facility (UK-FCF) [1, 2, 3, 4, 5] .
In a natural river,large numbers of vegetation often live along the bank or on the floodplain. Huang et al. [6] and Yang et al. [7] experimentally investigated the effects of vegetation on the three-dimensional (3D) flow characteristics. James and Makoa [8] found that the conveyance capacity was significantly reduced by the vegetation. Tang and Knight [9] proposed an analytical model to predict the lateral velocity distribution in the compound channel with emergent oneline rods. Liu et al. [10] developed the model by considering the submergence of the vegetation on the floodplain. Huai et al. [11, 12] presented the methods by analyzing the force balance for a unit water body in the vegetated compound channel,and obtained good modeling results in the three cases with different vegetation densities. Liu et al. [13] discovered that different types of vegetation (e.g.,tree,shrub,and grass) affected the intensity and the rotational direction of secondary flows differently. From these studies,an interesting phenomenon can be noticed that the vegetation on the bank or floodplain may avoid erosion,while at the same time,the conveyance capacity for the whole channel may decrease significantly because the streamwise velocity in the vegetated area is much reduced. Therefore,when we are considering the erosion protection for a channel bed or beautiful landscape for some man-made channels,we must think about some specific types of vegetation along the bank or on the floodplain. If the floodplain is developed as the farmland or even the house living place which are needed to be protected well,building flood embankments may be a good choice. Therefore,the satisfied or negative effect of vegetation in a specific channel mainly depends on the demand of human beings. Since the vegetation is a two-side sword to river engineering,its effect must be considered and the corresponding stage-discharge changes have to be studied further.
Some scholars [14, 15, 16, 17, 18, 19] have investigated the flow characteristics and the stage-discharge relationship in single channels,which may be much helpful to predict the flow discharge. In the compound channel with smooth floodplain,the single-channel method seams easily to estimate the discharge. However,the predictive result is not accurate. Knight and Demetriou [20] ,Knight and Hamed [21] ,Tang et al. [22] ,and Wormleaton and Merrett [23] summarized the dividedchannel methods by different ways of panel division,and the predictions were much closer to experimental data. Ackers [24] proposed the coherence method (COHM) for predicting the conveyance capacity of straight compound channels. Yang et al. [25] ,Zeng et al. [26] ,and Liu and Dong [27] showed the methods for assessing the stage-discharge relationship by considering the momentum transfer. The differences among their models were that the momentum exchange was considered between different areas. Yang et al. [28] developed a simple but effective method to estimate the discharge capacity based on the energy concept. Liao and Knight [29] and Abril and Knight [30] proposed the analytical method and finite element model for the discharge prediction,respectively,based on the Shiono and Knight method [31] . The practical predictive method for the total discharge derived from the dimensional analysis presented by Shiono et al. [32] was available to the use in meandering compound channels. Many other methods were proposed for the discharge prediction in compound channels [33, 34, 35, 36, 37, 38, 39, 40] . However,in these methods, the effect of the secondary flow was ignored,and the obtained modeling results were not good enough. Moreover,the research information about the stage-discharge relation in the vegetated compound channel is seldom.
The goal of this paper is to propose a reasonable and simple method for stage-discharge prediction. First of all,the governing equation for the discharge per unit width in the vegetated compound channel is derived from the flow continuity equation and the momentum equation, leading to a two-dimensional (2D) analytical solution to the discharge per unit width. Then, a numerical integral method,named the compound trapezoidal formula,is used to obtain the approximate solutions for the sub-area discharge and the total discharge. The predictive capability of the model is verified by the experimental data from the UK-FCF. Finally,the effects of two crucial parameters on the total discharge are discussed and analyzed. This research may provide the predictive method of the stage-discharge curve for the hydraulic engineering project in the natural river with vegetation on the floodplain. 2 Model development
To predict the sub-area discharge and total discharge in the vegetated compound channel, the governing equation for the discharge per unit width is derived from the flow continuity and momentum equations. For the incompressible fluid,the flow continuity equation may be expressed as follows:
where x,y,and z are the streamwise,lateral,and vertical directions,respectively. U ,V ,and W are the temporal mean velocity components corresponding to the x-,y-,and z -directions, respectively.For the flow on the vegetated floodplain,the drag force due to vegetation must be considered, and the streamwise momentum equation may be shown as follows:
where g is the local gravitational acceleration. S is the channel bed slope. ρ is the flow density. T xx ,T yx ,and T zx are the Reynolds stresses on the planes perpendicular to the x-,y-,and z -directions,respectively. Fd is the drag force due to vegetation which may be expressed as where m is the number of plants per unit bottom area. β is the shape factor accounting for the vegetation type. Cd is the drag force coefficient,and D is the vegetation diameter. For the steady uniform flow,the longitudinal variation is neglected,i.e.,

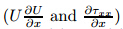 in Eq. (2) can be ignored.
in Eq. (2) can be ignored.Then,substituting Eqs. (1) and (3) into Eq. (2) yields
The depth-averaged equation may be obtained by integrating Eq. (4) over the local flow depth H(y). Due to the specific characteristic of the velocity in the vertical direction,i.e.,

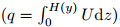 ,the governing equation for
the discharge per unit width may be obtained as follows:
where τ
b
is the bed shear stress,and Bs
is the factor corresponding to the inclined bed surface
defined by
,the governing equation for
the discharge per unit width may be obtained as follows:
where τ
b
is the bed shear stress,and Bs
is the factor corresponding to the inclined bed surface
defined by

Since the eddy viscosity has the dimension of m 2 /s and is often related to the shear velocity U* and the local flow depth H(y),the dimensionless eddy viscosity can be defined by
where λ is the lateral dimensionless eddy viscosity,regarded as a “catch all” parameter to describe various 3D effects [31] . In addition,the friction factor f ,which is defined by



According to the above introduction of parameters,the depth-averaged governing equation can be expressed as follows:
where Γ is the secondary coefficient expressed as

In the domain with constant flow depth,the analytical solution of the discharge per unit width for Eq. (9) is shown as follows:
where A1 and A2 are integral constants,and

For the domain with linearly varying flow depth

 |
| Fig. 1 Cross-section of compound channel |
The analytical solution of Eq. (11) is presented as follows:
where C1 and C2 are integral constants,and

To obtain the sub-area discharge Qi
,Eqs. (10) and (12) must be integrated laterally in the
specific area. However,from Eqs. (10) and (12),it can be noticed that their analytical integral
results,i.e.,Qi =
 qdy,may be hardly obtained. Therefore,a simple but available n umerical
method,i.e.,the compound trapezoidal formula,is used here to calculate the approximate
solution. The main idea of this method is to use the sum of all small divided trapezoidal areas
to stand for the real integral result. The theoretical schematic diagram for the main channel
of a vegetated compound channel is shown in Fig. 2. Each sub-area has been divided into N
equal parts. Therefore,there are N +1 dividing points,and the numerical integral results of Qi
are shown as follows:
qdy,may be hardly obtained. Therefore,a simple but available n umerical
method,i.e.,the compound trapezoidal formula,is used here to calculate the approximate
solution. The main idea of this method is to use the sum of all small divided trapezoidal areas
to stand for the real integral result. The theoretical schematic diagram for the main channel
of a vegetated compound channel is shown in Fig. 2. Each sub-area has been divided into N
equal parts. Therefore,there are N +1 dividing points,and the numerical integral results of Qi
are shown as follows:
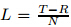 ,y
k
and y
k+1 are the dividing points,f (y) is
the integrand of Eq. (10) or Eq. (12),R is the integral lower limit,i.e.,R = yo
,and T is the
integral upper limit,i.e.,T = yN .
,y
k
and y
k+1 are the dividing points,f (y) is
the integrand of Eq. (10) or Eq. (12),R is the integral lower limit,i.e.,R = yo
,and T is the
integral upper limit,i.e.,T = yN .
 |
| Fig. 2 Illustration of compound trapezoidal formula for main channel in vegetated compound channel |
The approximate results of Qi are much closer to the real ones with bigger N ,and equal real values when N → +∞. The total discharge can be expressed as follows:
where i = 1,2,3,4,presenting the main channel,the main channel side slope,the floodplain (or sometimes the vegetated floodplain),and the floodplain side slope,respectively. 3 Determination of integral constantsThe cross-section of a compound channel is divided into four sub-areas (see Fig. 1). The unknown integral constants in Eqs. (10) and (12) may be eliminated by the chosen appropriate boundary conditions. In this paper,the boundary conditions are shown as follows:
(i) q = 0 at the remote boundary;
(ii) At each domain junction,q i = q i+1 .
(iii) At the junction of divided areas,the unit force is continuous,i.e.,
is continuous,i.e.,

(iv) There is no momentum exchange  = 0) at the centerline of the main channel
in the symmetric compound channel,i.e.,
= 0) at the centerline of the main channel
in the symmetric compound channel,i.e.,
 4 Input parameters
4 Input parameters
To use Eqs. (10) and (12) to predict the sub-area discharge and the total discharge,f ,λ, Cd ,β,and Γ are required to be addressed in details. The subscript (i) for all the parameters has the same meaning as the foregoing section. 4.1 Friction factor f
To predict f i in the compound channel with or without vegetation,the following modified form of the Colebrook-White equation is used:
where ν is the kinematic viscosity,k s is the equivalent sand roughness height obtained from the relationship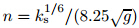 proposed by Ackers
[41]
. Rameshwaran and Shiono
[42]
suggested
φ = 12.3 and φ = 1.2 for the non-vegetated domain and the vegetated domain,respectively.
4.2 Dimensionless eddy viscosity λ
proposed by Ackers
[41]
. Rameshwaran and Shiono
[42]
suggested
φ = 12.3 and φ = 1.2 for the non-vegetated domain and the vegetated domain,respectively.
4.2 Dimensionless eddy viscosity λ λ1 is taken as the standard value 0.067,i.e.,κ/6,where κ is the Karman constant. It almost holds as a constant in the main channel [31] . On the floodplain,Abril and Knight [30] proposed a relationship as follows:

In the range of the rod Reynolds numbers in the experiments of FCF02 and FCF07
[42]
,i.e.,
1 000 Re
Re  10 000,Cd
is assumed to be about 1.0.
4.4 Shape factor β
10 000,Cd
is assumed to be about 1.0.
4.4 Shape factor β
In the vegetated case (FCF07),the shape factor β reflects the influence of the vegetation type,and it may be set as 1.0 because cylindrical rods are used to simulate the vegetation on the floodplain. 4.5 Secondary flow coefficient Γ
The secondary flow coefficient Γi in the sub-area is defined as the integral result of
 over the local flow depth (see Eq. (9)). It is of the same dimension as the gravity term ρgSH (y).
Therefore,in the non-vegetated compound channel,the relationship between Γi
and ρgSH (y)
may be built as follows:
over the local flow depth (see Eq. (9)). It is of the same dimension as the gravity term ρgSH (y).
Therefore,in the non-vegetated compound channel,the relationship between Γi
and ρgSH (y)
may be built as follows:
In the vegetated compound channel,the value of Γi changes with Dr . The relation may be presented as follows:
where αi is a ratio coefficient,defined as 1.2 and 0.6 for the main channel and the floodplain [42] , respectively. 5 Experimental dataTwo series groups of experimental data from the UK-FCF are used here,i.e.,the nonvegetated case FCF02 and the vegetated case FCF07. The data are collected from the web www.flowdata.bham.ac.uk. The experimental program is briefly described here,and the details may be found in Ref. [43]. The flume in the UK-FCF is 60 m long and 10 m wide with a maximum discharge of 1.1 m 3 /s. Within the large-scale flume,a variety of compound channels can be built with different geometries (straight,skewed,or meandering) and various floodplain conditions (smooth or rough). Typical cross-sections of straight compound channel are shown in Fig. 1, and four sub-areas are divided,i.e.,(1) main channel,(2) main channel side slope,(3) floodplain or vegetated floodplain,and (4) floodplain side slope. Only half of the compound channel is discussed because of the flow symmetry. The general bed slope S is set as 1.027×10 3 . The main channel width b is 0.75 m. The bankfull height h is 0.15 m. B = 3.15 m,and s 2 = s 4= 1. For the vegetated case,the rods are used to simulate the floodplain vegetation with the diameter D of 0.025 m and the density of 12 rods per m 2 . All the vegetation in the FCF07 case is emergent. The 3D turbulence data are recorded by the laser doppler anemometer (LDA) system at different relative flow depths,i.e.,
Dr = 0.041,0.117,0.157,0.198,0.242,0.298,0.396,0.479
for the FCF02 case andDr = 0.038,0.094,0.150,0.193,0.248,0.315,0.399,0.504
for the FCF07 case. 6 Calculation procedureIn the compound channel without any vegetation,the stage-discharge curve may be obtained by inputting several calculation parameters,i.e.,H,S,B,b,h,s,f ,λ,and Γ,for each subarea. When the vegetation is planted on the floodplain,some other parameters about the vegetation may be needed further,such as m,Cd ,β,and D. The calculation procedure of the stage-discharge curve is shown clearly as follows:
(i) Use the boundary conditions presented in Section 3,and input the calculation parameters shown at the beginning of this section to obtain the integral constants (A1,A2,C1 and C2) of Eqs. (10) and (12) in each sub-area.
(ii) Use Eq. (13) to obtain the Qi in the four sub-areas.
(iii) Obtain the total discharge Q by Eq. (14).
To well understand the calculation procedure,a case (FCF020801) of FCF02 with H = 0.287 9 m is taken as an example. Firstly,the integral constants A1,A2,C1 and C2in Eqs. (10) and (12) are obtained by the appropriate boundary conditions and inputting calculation parameters. For the main channel,
A1 = A2 = −0.002 5,w = 0.063 6.
For the main channel side slope,C1 = 12.866 5,C2 = 2.161 5 × 10 −4 ,w1 = −1.493 1,w2 = −11.688 7.
For the floodplain,A1 = 9.309 9 × 10 −23 ,A2 = 1 437.651 5,w = 0.000 9.
For the floodplain side slope,C1 = 0.020 5,C2 = 0,w1 = −0.323 4,w2 = 0.064 5.
Then,one can choose the appropriate lower and upper limits for each sub-area,and obtain the predictive Qi (see Table 1) by using Eq. (13). The Q calculated by Eq. (14) is 0.558 3 m 3 /s,and the experimental total discharge is 0.557 m 3 /s. |
The relative error Φ is used here. It is defined by
where Qpre is the predictive discharge,and Qexp is the experimental discharge.The relative error Φ for the total discharge of FCF020801 is only 0.233%. All the other cases of FCF02 and FCF07 are experienced in the identical calculation procedure to obtain the sub-are discharge and the total discharge. 7 Application
This model is applied in the FCF02 and FCF07 cases to predict the sub-area discharge. The results are shown in Fig. 3. In this figure,the main channel discharge is the total of Q1 + Q2, while the floodplain one is the sum of Q3 + Q4. The discharges of the main channel and floodplain are presented as the percentage form of the total discharge. For the non-vegetated cases (FCF02),Fig. 3(a) shows that the main channel discharge is dominant when Dr < 0.45. If the flow depth continues to increase,the dominant place of the main channel for the total discharge will be substituted by the floodplain. For the vegetated cases (FCF07),the discharge of the main channel always keeps the dominant position when 0 < Dr < 0.6. The ratio distribution of FCF07 is entirely different from that of FCF02,indicating that vegetation significantly reduces the conveyance capacity on the floodplain. In addition,the results in Fig. 3 demonstrate that the predictive ability of this model for each sub-area is quite good.
 |
| Fig. 3 Percentages of sub-area discharge for main channel and floodplain |
The total discharges of FCF02 and FCF07 are carried out,and shown in Fig. 4 when the sub-area discharges are all obtained. From Fig. 4,we can see that though the stage-discharge curves seem following different inclinations,the predictions are still close to the experimental data. In addition,it is noticeable that the total discharge of FCF07 is affected by the floodplain vegetation significantly. When the flow depth H of FCF02 reaches 0.287 9 m,the corresponding discharge is 0.557 1 m 3 /s. By contrast,the total discharge of FCF07 is only about half of that of FCF02,i.e.,0.271 7 m 3 /s,when H = 0.302 5 m. Figure 4 also shows the relative errors Φ for the cases FCF02 and FCF07. In the FCF02 case,all values of Φ hold within ±3% except the case with the lowest flow height,i.e.,H = 0.156 49 m,where Φ is -7.8%. In the FCF07 case, the biggest Φ is -6.56%,appearing when H = 0.155 86 m with the lowest water level. From the above error analysis,the predictive capability of the stage-discharge curve of this model is quite good in whether the non-vegetated compound channel or the vegetated compound channel.
 |
| Fig. 4 Experimental and predictive stage-discharge curves with relative errors |
In this model,the effects of two coefficients,i.e.,the number of the divided panel N in the integral interval and the secondary flow coefficient Γ,on the total discharge are not reported. Therefore,their effects on the conveyance capability are necessarily discussed separately. 8.1 Effect of integral interval divided number on total discharge
The value of N must be chosen according to the required accuracy. To show the influence of N on the total discharge Q,it is chosen as 2,4,8,16,32,64,and 128,respectively,for the four sub-areas. The comparison of the predictive results are shown in Fig. 5. From the figure,we can see that N > 64 is suitable because the maximum value of the absolute difference ε between the predictions with N = 64 and N = 128 is less than 0.001 m 3 ·s -1 in both the FCF02 and FCF07 cases. Therefore,N = 128 is used in the main channel and the floodplain. However, due to the much faster calculation convergence speed in the relatively smaller size domains (domains shown as (2) and (4) in Fig. 1),the absolute difference between the predictive results with N = 16 and N = 32 also meets the required accuracy ε < 0.001 m 3 ·s -1 . Hence,N is selected as 32 in the two side sloping areas.
 |
| Fig. 5 Influence of N in integral interval on total discharge |
In addition,the value of N affects the results more significantly in the vegetated case (FCF07),especially when the flow depth is deep,when compared with the non-vegetated one (FCF02). Besides,the increasing inclinations of the total discharge in both cases are totally different. 8.2 Effect of secondary flow coefficient on total discharge
In the non-vegetated case (FCF02),the effects of Γ1 (defined by Eq. (16)) on the total discharge are shown in Fig. 6. A parallel manner of the stage-discharge curves is observed,i.e., k 1 ∈ [0.0,1.0],indicating that Γ 1 is an important parameter. However,Fig. 7 shows that the total discharge is insensitive to Γ3 when k 3 varies from -1.0 to 0.0. Figures 6 and 7 also show that the predictive discharges seem unacceptable when the secondary flows in the main channel and on the floodplain are neglected,i.e.,k 1 = 1.0 and k 3 = 1.0. Theoretically,this assumption is unreasonable. The larger values of k 1 and k 3 are considered,the smaller the total discharge predictions may be obtained.
 |
| Fig. 6 Effects of Γ1 in main channel on stage-discharge curve in FCF02 |
 |
| Fig. 7 Effects of Γ3 on floodplain on stagedischarge curve in FCF02 |
For the vegetated case (FCF07),Figs. 8 and 9 show the relation of the stage-discharge when α1 and α3 increase from 0 to 1.0 in the main channel and on the floodplain,respectively. The effects of α1 on the total discharge are entirely different from that of k 1 because of the different definitions of Γ i (see Eqs. (16) and (17)). It can also seen that the deeper the flow depth is, the more serious effect of α1 on predictions is. However,the similar phenomenon in the FCF02 case is observed that the stage-discharge curve is insensitive to Γ3 (see Fig. 9). Though the secondary flows on the floodplain are weak [7] ,their effects on the stage-discharge curve cannot be ignored.
 |
| Fig. 8 Effects of Γ1 in main channel on stage-discharge curve in FCF07 |
 |
| Fig. 9 Effects of Γ3 on floodplain on stagedischarge curve in FCF07 |
In general,the stage-discharge relation is sensitive to Γ1 while insensitive to Γ3 in the FCF02 and FCF07 cases. To predict the total discharge reasonably,the effects of the secondary flows have to be considered appropriately in each sub-area,otherwise poor results will be obtained when the secondary currents are ignored. 9 Conclusions
(i) The governing equation for the discharge per unit width in the vegetated compound channel is derived from the flow continuity equation and the momentum equation. The analytical solutions contain four crucial parameters which are associated with the bed friction,the drag force,the lateral momentum transfer,and the secondary flow.
(ii) A numerical integral method,named the compound trapezoidal formula,is firstly used to obtain the approximate solution for the sub-area discharge Qi . Then,the total discharge Q is obtained. All the input parameters are introduced,and a simple hand calculation procedure is presented.
(iii) A comparison with two groups of published experimental data (FCF02 and FCF07) shows that the presented model can well predict not only the stage-discharge curve but also the sub-area discharge in both non-vegetated and vegetated compound channels. The predictive results of the main channel discharge (Q1 + Q2) and the floodplain discharge (Q3 + Q4) show that Q1 + Q2 keeps the dominant place in the vegetated channel when 0< Dr < 0.6. However, in the non-vegetated channel,Q1 + Q2 dominates the total discharge when Dr < 0.45,and Q3 + Q4 dominates the dominant place when Dr > 0.45. The relative errors of FCF02 and FCF07 are mostly within ±3% and ±4%,respectively.
(iv) The effects of the divided number N in the integral interval and the secondary flow coefficient (Γ) on the total discharge are discussed and analyzed separately. The value of N may be chosen according to the required accuracy. The predictive result is accurate enough when N = 128 in the main channel and on the floodplain and when N = 32 in the two side sloping areas. In the non-vegetated and vegetated cases,Γ1 is a sensitive parameter while Γ3 is an insensitive parameter to the total discharge. The effect of the secondary flows cannot be ignored during the calculation. Otherwise,poor results will be obtained.
| [1] | Atabay, S. Stage-Discharge, Resistance, and Sediment Transport Relationships for Flow in Straight Compound Channels, Ph.D. dissertation, University of Birmingham, Birmingham (2001) |
| [2] | Knight, D. W., Omran, M., and Tang, X. Modeling depth-averaged velocity and boundary shear in trapezoidal channels with secondary flows. Journal of Hydraulic Engineering, 133, 39-47 (2007) |
| [3] | Tang, X., Knight, D. W., and Sterling, M. Analytical model of streamwise velocity in vegetated channels. Proceedings of the ICE-Engineering and Computational Mechanics, 164, 91-102 (2011) |
| [4] | Yang, Z. H., Gao, W., and Huai, W. X. Study on the secondary flow coefficient of over- bank flow. Applied Mathematics and Mechanics (English Edition), 31(6), 709-718 (2010) DOI 10.1007/s10483-010-1305-9 |
| [5] | Yang, K. J., Nie, R. H., Liu, X. N., and Cao, S. Y. Modeling depth-averaged velocity and bound- ary shear stress in rectangular compound channels with secondary flows. Journal of Hydraulic Engineering, 139, 76-83 (2013) |
| [6] | Huang, B. S., Lai, G. W., Qiu, J., and Lin, S. Z. Hydraulics of compound channel with vegetated floodplains. Journal of Hydraulics, 14, 23-28 (2002) |
| [7] | Yang, K. J., Cao, S. Y., and Knight, D. W. Flow patterns in compound channels with vegetated floodplains. Journal of Hydraulic Engineering, 133, 148-159 (2007) |
| [8] | James, C. S. and Makoa, M. J. Conveyance estimation for channels with emerged vegetation boundaries. Proceedings of the ICE-Water Management, 159, 235-243 (2006) |
| [9] | Tang, X. and Knight, D.W. Lateral distribution of streamwise velocity in compound channels with partially vegetated floodplains. Science in China Series E: Technological Sciences, 52, 3357-3362 (2009) |
| [10] | Liu, C., Luo, X., Liu, X. N., and Yang, K. J. Modeling depth-averaged velocity and bed shear stress in compound channels with emerged and submerged vegetation. Advances in Water Resources, 60, 148-159 (2013) |
| [11] | Huai, W. X., Xu, Z. G., Yang, Z. H., and Zeng, Y. H. Two-dimensional analytical solution for a partially vegetated compound channel flow. Applied Mathematics and Mechanics (English Edition), 29(8), 1077-1084 (2008) DOI 10.1007/s10483-008-0811-y |
| [12] | Huai, W. X., Gao, M., Zeng, Y. H., and Li, D. Two-dimensional analytical solution for compound channel flows with vegetated floodplains. Applied Mathematics and Mechanics (English Edition), 30(9), 1121-1130 (2009) DOI 10.1007/s10483-009-0906-z |
| [13] | Liu, C., Shan, Y. Q., Yang, K. J., and Liu, X. N. The characteristics of secondary flows in compound channels with vegetated floodplains. Journal of Hydrodynamics, 25, 422-429 (2013) |
| [14] | Folkard, A. M. Vegetated flows in their environmental context: a review. Proceedings of the ICE- Engineering and Computational Mechanics, 164, 3-24 (2011) |
| [15] | Liao, H. S. and Knight, D. W. Analytic stage-discharge formulae for flow in straight trapezoidal open channels. Advances in Water Resources, 30, 2283-2295 (2007) |
| [16] | White, B. L. and Neph, H. M. Shear instability and coherent structures in shallow flow adjacent to a porous layer. Journal of Fluid Mechanics, 593, 1-32 (2007) |
| [17] | Li, C. W. and Zeng, C. 3D numerical modeling of flow divisions at open channel junctions with or without vegetation. Advances in Water Resources, 32, 49-60 (2009) |
| [18] | Barrett, L., Wright, N. G., and Sterling, M. A comparison of 2D and 3D simulations of the River Blackwater. Proceedings of the ICE-Engineering and Computational Mechanics, 164, 217-232 (2011) |
| [19] | McGahey, C., Samuels, P. G., Knight, D. W., and O'Hare, M. T. Estimating river flow capacity in practice. Journal of Flood Risk Management, 1, 23-33 (2008) |
| [20] | Knight, D. W. and Demetriou, J. D. Flood plain and main channel flow interaction. Journal of the Hydraulic Engineering, 109, 1073-1092 (1983) |
| [21] | Knight, D. W. and Hamed, M. E. Boundary shear in symmetrical compound channels. Journal of the Hydraulic Engineering, 110, 1412-1430 (1984) |
| [22] | Tang, X., Knight, D. W., and Samuels, P. G. Variable parameter Muskingum-Cunge method for flood routing in a compound channel. Journal of Hydraulic Research, 37, 591-614 (1999) |
| [23] | Wormleation, P. R. and Merrett, D. J. An improved method of calculation for steady uniform flow in prismatic main channel/flood plain sections. Journal of Hydraulic Research, 28, 157-174 (1990) |
| [24] | Ackers, P. Flow formulae for straight two-stage channels. Journal of Hydraulic Research, 31, 509-531 (1993) |
| [25] | Yang, K. J., Liu, X. N., Cao, S. Y., and Huang, E. Stage-discharge prediction in compound channels. Journal of Hydraulic Engineering, 140, 06014001 (2014) |
| [26] | Zeng, Y. H., Wang, Y. H., and Huai, W. X. Hydraulic calculation of steady uniform flows in trapezoidal compound open channels. Applied Mathematics and Mechanics (English Edition), 31(8), 947-954 (2010) DOI 10.1007/s10483-010-1329-z |
| [27] | Liu, P. Q. and Dong, J. R. Hydraulic computation of steady-uniform flows in open channels with compound cross section (in Chinese). Journal of Yangtze River Scientific Research Institute, 12, 61-66 (1995) |
| [28] | Yang, Z. H., Gao, W., and Huai, W. X. Estimation of discharge in compound channels based on energy concept. Journal of Hydraulic Research, 50, 105-113 (2012) |
| [29] | Liao, H. S. and Knight, D. W. Analytic stage-discharge formulas for flow in straight prismatic channels. Journal of Hydraulic Engineering, 133, 1111-1122 (2007) |
| [30] | Abril, J. B. and Knight, D. W. Stage discharge prediction for rivers in flood applying a depth averaged model. Journal of Hydraulic Research, 42, 616-629 (2004) |
| [31] | Shiono, K. and Knight, D.W. Turbulent open channel flows with variable depth across the channel. Journal of Fluid Mechanics, 222, 617-646 (1991) |
| [32] | Shiono, K., Al-Romaih, J. S., and Knight, D. W. Stage-discharge assessment in compound mean- dering channels. Journal of Hydraulic Engineering, 125, 66-77 (1999) |
| [33] | Greenhill, R. K. and Sellin, R. H. J. Development of a simple method to predict discharges in compound meandering channels. Proceedings of the ICE-Water, Maritime & Energy, 101, 37-44 (1993) |
| [34] | Horritt, M. S. and Wright, N. G. A mixing length model for estimating channel conveyance. Proceedings of the ICE-Water Management, 166, 165-174 (2011) |
| [35] | Myers, W. R. C., Lyness, J. F., and Cassells, J. B. Influence of boundary roughness on velocity and discharge in compound river channels. Journal of Hydraulic Research, 39, 311-319 (2000) |
| [36] | Sechin, G., Mamak, M., Atabay, S., and Omran, M. Discharge estimation in compound channels with fixed and mobile bed. Sadhana, 34, 923-945 (2009) |
| [37] | Wormleaton, P. R., Allen, J., and Hadjipanos, P. Discharge assessment in compound channel flow. Journal of Hydraulic Division, 108, 975-993 (1982) |
| [38] | Karamisheva, R. D., Lyness, J. F., Myers,W. R. C., Cassells, J. B. C., and O'Sullivan, J. Overbank flow depth prediction in alluvial compound channels. Proceedings of the ICE-Water Management, 159, 195-205 (2006) |
| [39] | Lambert, M. F. and Myers, W. R. C. Estimating the discharge capacity in straight compound channels. Proceedings of the ICE-Water, Maritime & Energy, 130, 84-94 (1998) |
| [40] | Darby, S. E. and Thorne, C. R. Predicting stage-discharge curves in channels with bank vegetation. Journal of Hydraulic Engineering, 122, 583-586 (1996) |
| [41] | Ackers, P. Hydraulic Design of Straight Compound Channels, Technical Report, HR Wallingford, 1-139 (1991) |
| [42] | Rameshwaran, P. and Shiono, K. Quasi two-dimensional model for straight overbank flows through emergent vegetation on floodplains. Journal of Hydraulic Research, 45, 302-315 (2007) |
| [43] | Knight, D. W. and Sellin, R. H. J. The SERC flood channel facility. Journal of Institution Water Environment and Management, 1, 198-204 (1987) |
 2014, Vol. 35
2014, Vol. 35




















