Shanghai University
Article Information
- S. ASGHAR, Q. HUSSAIN, T. HAYAT, F. ALSAADI. 2014.
- Hall and ion slip effects on peristaltic flow and heat transfer analysis with Ohmic heating
- Appl. Math. Mech. -Engl. Ed., 35(12): 1509-1524
- http://dx.doi.org/10.1007/s10483-014-1881-6
Article History
- Received 2013-9-27;
- in final form 2014-4-3
2. Department of Electrical and Computer Engineering, Faculty of Engineering, King Abdulaziz University, Jeddah 21589, Saudi Arabia;
3. Department of Mathematics, Quaid-i-Azam University, Islamabad 44000, Pakistan
The transportation of the bio-fluids from one place to another place caused by the propulsive movement of biological systems having smooth muscle tubes is known as peristalsis. The mechanism can be seen in the flow of urine from kidney to bladder through ureter,passage of chyme through the gastrointestinal tract,movement of spermatozoa in the cervical canal,embryo motion in non-pregnant uterus,bile movement in a bile duct,transport of lymph in lymphatic vessels,circulation of blood in small blood vessels,arterioles,and venules in capillaries. It also works in many important technological applications such as blood pumps in hurt-lung machine and finger and roller pumps for pumping of corrosive and toxic materials. Peristaltic flow has attracted the attention of many researchers and scientists due to its occurrence in natural phenomena and applications in biomechanical systems. Latham [1] was the first who explored the mechanism of peristalsis through experiments. The theoretical results obtained by Shapiro [2] were found to be in good agreement with the experimental results given by Latham [1] . Later on,many studies on this topic have been added in the literature under different situations and configurations [3, 4, 5, 6, 7, 8, 9, 10, 11] .
The heat transfer analysis is important to obtain the information about the blood flow rate through the initial thermal conditions and the thermal clearance rate. The blood flow can be estimated through the dilation technique. The thermal clearance in this process is watched when heat is either injected or generated locally. The role of bioheat transfer is frequently used in cryosurgery,laser therapy,and cancer tumor treatment causing hypothermia and destroying undesirable tissues. The study of heat transfer in peristaltic flows is important in some biomedical processes like oxygenation and hemodialysis. Moreover,this phenomenon helps in the transportation of the sanitary fluids,blood pumps in heart lung machine,and the transportation of corrosive materials where the fluid contact with machinery is prohibited. The normal blood temperature of a man is about 37 ℃ . When it increases to 41 ℃ C or above,irretrievable damage will take place in the plasma proteins. F ocusing on such facts,Ogulu [12] discussed the effect of heat generation on low Reynolds number fluid and mass transport in a single lymphatic blood vessel with uniform magnetic field. Mekheimer and Abd-Elmaboud [13] performed the heat transfer analysis on the peristaltic transport of electrically conducting Newtonian fluid in a vertical annulus. Vajravelu et al. [14] discussed the peristalsis with heat transfer by considering the viscous fluid in a vertical porous annulus. Srinivas and Kothandapani [15] dealt with peristalsis and heat transfer. Nadeem and Akbar [16] considered the effects of variable viscosity on heat transfer analysis of peristaltic flow of magnetohydrodynamic (MHD) Newtonian fluid. Radhakrishnamacharya and Srinivasulu [17] studied the influence of wall properties on peristaltic transport with heat transfer. Hayat et al. [18, 19, 20] and Abd-Elmaboud et al. [21] analyzed the peristaltic mechanism with heat transfer.
In all the above mentioned works,Hall and ion slip effects were neglected in applying the Ohm’s law as they have no remarkable effect for a weak magnetic field. However,the current trend in the application of magnetohydrodynamics is towards a strong magnetic field so that the effect of the electromagnetic force is noticeable. Therefore,the Hall and ion slip currents are important and they have remarkable effects on the magnitude,on the direction of the current density,and consequently on the magnetic force term [22] . The effects due to the Hall current become significant when the Hall parameter (the ratio of electron-cyclotron frequency and the electron-atom-collision frequency) is high. This situation occurs as a result of high magnetic field or low collision frequency. The previous related works in these directions are given by Hayat et al. [23] ,Abo-Eldahab et al. [24, 25] ,Haroun [26] ,and Mekheimer et al. [27] . The effects of Hall and ion slip currents with heat transfer are likely to be important in many situations as well as in engineering applications in areas like Hall accelerators,power generators,MHD accelerators,refrigeration coils,electric transformers,and heating elements. The study of the effect of a magnetic field and the Hall currents on the blood flow through an artery with a mild stenosis may be helpful in understanding the magnetic resonance angiography,which is one of the radiological investigations done for atherosclerosis [28] .
The above literature review indicates that no attempt has been made to explain the combined effects of Hall and ion slip currents and Ohmic heating on the peristaltic transport of electrically conducting viscous fluid with heat transfer. In fact,the Joule heating effect arises from the applied electric field and fluid electrical resistivity. Studying the heat transfer with Joule heating effects is very important for many applications in food industries and biomedical engineering. One of the important applications of electroosmosis is the fluid delivery in lab-on-a-chip devices, where one deals with thermally labile samples. The temperature rise due to the Joule heating can result in low column separation efficiency,reduction of analysis resolution,and even loss of injected samples. In addition,the viscous dissipation effects in the energy equation cannot be neglected. Such effects have an important role in the dynamics of fluids with strongly temperature-dependent viscosity because of the coupling between the energy and momentum equations. The heat generated by viscous friction produces a local temperature increase near the tube walls with a consequent decrease in the viscosity which may dramatically change the temperature and velocity profiles. The basic theme behind this theoretical work is to fill the gap in these directions. Therefore,the present attempt deals with such facts for peristaltic flow in an asymmetric channel. The modeled problems are first solved,and then the obtained solutions are analyzed carefully. 2 Problem description
Consider the peristaltic flow of an incompressible and electrically conducting viscous fluid in a two-dimensional asymmetric channel with the uniform width d 1 + d 2 . The channel length is assumed to be infinite along the X-axis,whereas the width of the channel bounded by two walls H1 and H2 is parallel to the Y -axis and hence perpendicular to the length. Two sinusoidal waves propagate along the upper and lower walls with a constant speed c,which cause the fluid to propel in the direction of wave propagation. It is pertinent to mention that there is no flow in the channel prior and the imposition of sinusoidal waves along the channel walls can introduce the disturbance in the fluid which consequently drives the flow inside the channel. The shapes of the channel walls in a laboratory reference frame is defined through the following expressions:
where H1 and H2 are the shapes of the upper and lower walls,respectively. The wall shapes are functions of the wave amplitudes b 1 and b 2 ,the wave length λ,the time t,the channel widths associated with the upper and lower halves of the channel d 1 and d 2 and the phase difference of two waves φ which varies in the interval 0 φ
φ  π. The channel’s asymmetry is produced due
to the different amplitudes and phases of the waves on the upper and lower walls. The values of
φ = 0 and φ = π retrieve the symmetric shape of the channel. When φ = 0,two waves become
out of phase,and when φ = π,the two waves are inphase along the channel walls. Moreover,
the quantities b
1 ,b
2 ,d
1 ,d
2
,and φ satisfy the following inequality:
Furthermore,the channel walls are assumed to be non-conducting,and two constant but different temperatures T1
and T2 are maintained at the upper and lower walls,respectively. It is
further assumed that the temperature at the upper wall is less than that at the lower wall,i.e.,
T1 < T2 . In addition,the fluid is conducted under the application of a uniform magnetic field
with the magnetic flux density vector B=(0,0,B0
). Since we are also interested to analyze the
effects of Hall and ion slip on the peristaltic flow,the values of necessary magnetic Reynolds
number for the case of partially ionized fluid is considered
[29]
. To maintain the mathematical
simplicity for this study,we ignore the effects through the change in the magnetic field due to
the change in the electric field.
2.1 Governing equations
π. The channel’s asymmetry is produced due
to the different amplitudes and phases of the waves on the upper and lower walls. The values of
φ = 0 and φ = π retrieve the symmetric shape of the channel. When φ = 0,two waves become
out of phase,and when φ = π,the two waves are inphase along the channel walls. Moreover,
the quantities b
1 ,b
2 ,d
1 ,d
2
,and φ satisfy the following inequality:
Furthermore,the channel walls are assumed to be non-conducting,and two constant but different temperatures T1
and T2 are maintained at the upper and lower walls,respectively. It is
further assumed that the temperature at the upper wall is less than that at the lower wall,i.e.,
T1 < T2 . In addition,the fluid is conducted under the application of a uniform magnetic field
with the magnetic flux density vector B=(0,0,B0
). Since we are also interested to analyze the
effects of Hall and ion slip on the peristaltic flow,the values of necessary magnetic Reynolds
number for the case of partially ionized fluid is considered
[29]
. To maintain the mathematical
simplicity for this study,we ignore the effects through the change in the magnetic field due to
the change in the electric field.
2.1 Governing equations The conservation of mass and the balance of momentum and energy are given by
In the above equations,d/dt is the sum of local and convective time derivatives,P is the pressure,V is the fluid velocity vector,ρ is the constant density,µ is the dynamic viscosity, J × B is the Lorentz force vector,T is the fluid temperature,c p is the specific heat,κ is the thermal conductivity,τ is the Cauchy stress tensor,τ ·L is the viscous dissipation term,and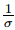 (J · J ) is the Joule heating term.
(J · J ) is the Joule heating term.The generalized Ohm’s law with Hall and ion slip effects is given by [24]
where J is the current density vector,σ is the fluid electrical conductivity,ωe is the cyclotron frequency,te is the electron collision time,and β i is the ion slip parameter. Using the Maxwell equations and solving Eq. (7) in J yield where U and V are the axial and transverse components of the fluid velocity ,respectively, i and j denote the unit vectors in the X- and Y -directions,respectively,βe is the Hall parameter expressed by β e = ωete ,and αe = 1 + β i β e. 2.2 Transformation and non-dimensionalizationTo transform our flow analysis from the laboratory reference frame to the wave reference frame,we use the standard Galilean transformations given by
where p and u,v are the pressure and the velocity components in the wave reference frame, respectively. Substituting these transformations in Eqs. (4)-(6) yields The dimensionless parameters for our problem are given by where δ,Re,P r,Ec,Br,and Ha represent the wave number,the Reynolds number,the Prandtl number,the Eckert number,the Brinkman number,and the Hartman number,respectively.Invoke these dimensionless parameters and introduce the stream function ψ * by writing the velocity components as
such that the continuity equation can be identically satisfied. Then,Eqs. (12)-(14) can be reduced to The above equations are subject to long wavelength assumption,i.e.,λ d
1,which means
that δ → 0. Moreover,the asterisks are omitted for simplicity.
d
1,which means
that δ → 0. Moreover,the asterisks are omitted for simplicity.The boundary conditions in the wave reference frame are expressed as follows:
where

Equation (18) indicates that p is a function of x only. Operating
 on Eq. (17) leads to
on Eq. (17) leads to

In this section,we will discuss the salient features of the peristaltic flow and the heat transfer under the influence of the Hall parameter β e,the ion slip parameter β i ,the Hartman number Ha,and the Brinkman number Br. The complicated integrals in the expressions of pressure rise and frictional forces are computed numerically by using built-in routine NIntegrate in MATHEMATICA-8.
The variation of pressure rise ∆Pλ over one cycle of the wave is shown in Fig. 1. It can be clearly seen that the pumping rate in the retrograde pumping region (∆Pλ > 0,Q < 0) decreases when β e and β i increase while increases when Ha increases. This situation remains the same in the peristaltic pumping region (∆Pλ > 0,Q > 0) up to the flow rate Q = 0.21. The situation is reverse when Q exceeds 0.21. In the copumping region (∆Pλ < 0,Q > 0), when β e and Ha increase,∆Pλ is disturbed in an opposite direction to that observed in the retrograde pumping region (∆Pλ > 0,Q < 0). Further,the maximum pressure,∆Pλ when Q = 0,is less in magnitude in the presence of Hall current and ion slip. The value of the flow rate Q when ∆Pλ = 0 is known as free pumping flux and denoted by Q0.
 |
| Fig. 1 Distribution of pressure rise ∆Pλ for a1 = 0.7,a2 = 0.8,d = 2,and φ = π/2 |
Table 1 is prepared to have a better look on Q0 for various values of β e ,β i ,and Ha. From Table 1 ,we can observe that Q0 increases when β e and β i increase whereas decreases when Ha increases. The effects of β e and β ion pumping in all pumping regions become more apparent for large fixed Ha. However,this observation for Q0 becomes true when either β e or β i varies and Ha is fixed and small.
The variations in the frictional forces Fλs (s = 1,2) at the upper and lower walls,respectively,can be seen in Fig. 2. The left-hand panels explain the variation of Fλ1 at the upper wall y = h 1(x),while the right-hand panels illustrate the variation of Fλ2 at the lower wall y = h 2(x). Figure 2(a) describes that Fλ1 increases when β e increases whilst decreases when Ha increases. This situation becomes reverse after the flow rate is appropriately chosen,i.e.,Q = −0.24. The variations of Fλ2 with different β e and Ha are given in Fig. 2(b). It can be seen from Fig. 2(b) that increasing β e increases Fλ2 for Q < −0.11 whereas decreases Fλ2 for Q > −0.11. Comparing Fig. 2(a) with Fig. 2(b),one can see that Fλ1 is less in magnitude when compared with Fλ2. From Figs. 2(c) and 2(d),it is noted that the impact of β i on Fλs is similar to that of β e on Fλs . Moreover,the effects of β e and β i on both Fλ1 and Fλ2 are more significant for higher values of Ha. Figure 2 also illustrates that there exist critical values,i.e.,Qh1 and Qh2 ,corresponding to Fλ1 = 0 and Fλ2 = 0,respectively. The critical values define that Fλs (s = 1,2) resist the flow when Q < Qhs (s = 1,2) and assist the flow when Q > Qhs (s = 1,2).
 |
| Fig. 2 Distribution of frictional forces Fλs (s = 1,2) at channel walls for a1 = 0.7,a2 = 0.8,d = 2, and φ = π/2 |
The critical values Qh1 and Qh2 for different values of β e,β i ,and Ha are presented in Table 2. We observe from Table 2 that Qhs (s = 1,2) increase when β e and β i increase. However, when Ha increases,Qhs (s = 1,2) decrease. Moreover,the critical values of Qhs (s = 1,2) vary at a sharp rate with different β e and β i for small Ha.
The effects of β e ,β i ,and Ha on the axial pressure gradient dp/dx are displayed in Fig. 3. The graphs are plotted within one wavelength x ∈ [−0.5,0.5]. The panels on the left-hand side depict the variation of dp/dx corresponding to the symmetric channel,and the right-hand panels represent the variation of dp/dx corresponding to the asymmetric channel. Figure 3(a) illustrates that the pressure gradient dp/dx is symmetric about x = 0 when the channel is symmetric. For all values of Ha,increasing β e decreases the pressure gradient dp/dx,and the effect becomes more significant when Ha is large. Moreover,the pressure gradient dp/dx increases as a result of increasing Ha. It can be seen from Fig. 3(b) that the effects of β e and Ha on dp/dx remain the same for the asymmetric channel case. However,the pressure gradient dp/dx is not symmetric when the channel is asymmetric. Increasing β i disturbs dp/dx in a similar way to that of β e(see Figs. 3(c) and 3(d)).
 |
| Fig. 3 Distribution of axial pressure gradient dp/dx for a1 = 0.5,a2 = 0.5,d = 1,and Q = −2 |
The profiles of the dimensionless velocity u for different values of β e ,β i ,and Ha are shown in Fig. 4. It is evident that the amplitude of u decreases when Ha increases. This is due to the fact that the magnetic body force (Lorentz force) increases in response to an increase in Ha. Such force offers resistance to the fluid flow. The behavior of βe on u depending on Ha can be explained through Figs. 4(a) and 4( b). It can be seen from Figs. 4(a) and 4(b) that an increase in βe gives an increase in the amplitude of u. In fact,an increase in βe decreases the effective conductivity (σ/((1 + βi βe) 2 + βe 2 )),and consequently decreases the magnetic damping force. Therefore,u increases. Figures 4(a) and 4(b) also illustrate that the impact of βe on u is more prominent against the higher values of the magnetic field. This means that when Ha is small,an increase in the value of βe slightly increases the amplitude of u. This is due to the gradual decrease in the magnetic damping force which is proportional to βe. Moreover, increasing βe with larger Ha greatly decreases the effective conductivity which rapidly reduces the magnetic damping force. Therefore,u increases. Figures 4(c) and 4(d) ensure that the effects of the ion slip parameter βi on u are similar to those of the Hall parameter βe . The comparison of left-hand panels with right-hand panels reveals that the magnitude of u in the asymmetric channel case is less than that in the symmetric channel case.
 |
| Fig. 4 Distribution of velocity profile u for a2 = 0.8,d = 1,Q = 1,and x = 0.1 |
The distributions of the temperature profile θ are displayed in Fig. 5. As shown in the figure,Fig. 5(a) indicates the combined effects of βe and Ha on θ. It is noted that θ increases when Ha increases. In fact,the Lorentz force increases when Ha increases,which opposes the motion of the fluid. Therefore,some energy is converted into the heat due to the frictional forces. Contrarily,an increase in βe decreases θ for all values of Ha. This is because of the result of decreasing the Joule dissipation which is proportional to (1/((1 + βi βe) 2 + βe 2 )). The temperature profile θ increases when Br increases (see Fig. 5(b)). When Br increases,the heat energy is stored in the fluid due to the frictional or drag forces,and thus θ increases. Moreover, the variation in θ with βe is more significant for larger values of Ha and Br,which is due to the change in the viscous and Joule dissipations. Figures 5(c) and 5(d) explain the effects of βi on θ,which depend on Ha and Br,respectively. Here,one can see that the effects of βi on θ are similar to the effects of βe on θ in a qualitative manner.
 |
| Fig. 5 DDistribution of θ for a1 = 0.7,a2 = 0.8,d = 1,φ = π/2,Q = 0.6,and x = 0.1 |
The effects of βe ,βi ,Ha,and Br on the heat transfer coefficient Z at the upper wall y = h 1(x) are displayed in Fig. 6. In Fig. 6,the plots of Z are sketched for one wavelength x ∈ [−0.5,0.5]. Clearly,for all Ha and Br,Z decreases in magnitude in response to the increases in βe and βi . On the other hand,Z increases in magnitude when either Ha or Br increases. Figure 6 also indicates that the variations of Z with varying βe and βi become more prominent for large values of Ha and Br.
 |
| Fig. 6Distribution of Z at upper wall for a1 = 0.3,a2 = 0.4,d = 1,φ = π/4,and Q = 1.5 |
Figures 7-9 show the effects of βe ,βi ,and Ha on trapping. In all these figures,(a),(c),and (e) correspond to the symmetric channel,and (b),(d),and (f ) correspond to the asymmetric channel where the asymmetry of the channel is considered only through the phase difference. From Fig. 7,we can see that when βe increases,the size of the trapped bolus increases. Moreover, the bolus is symmetric about the center line for the symmetric channel. The trapped bolus tends to shift in the opposite direction of the wave propagation when the channel is asymmetric. This can be attributed to the different phase angles. Similar effects of βi on the size of the trapped bolus are seen through Fig. 8. However,opposite effects on trapping are observed in Fig. 9 where an increase in Ha yields a decrease in the size of the trapped bolus.
 |
| Fig. 7 Streamlines for different βe and φ in symmetric (left panels) and asymmetric (right panels) channels with a1 = 0.5,a2 = 0.5,d = 1,Q = 1.4,Ha = 1,and βi = 0.5 |
 |
| Fig. 8 Streamlines for different βi and φ in symmetric (left panels) and asymmetric (right panels) channels with a1 = 0.5,a2 = 0.5,d = 1,Q = 1.4,Ha = 1.5,and βe = 0.5 |
 |
| Fig. 9 Streamlines for different Ha and φ in symmetric (left panels) and asymmetric (right panels) channels with a1 = 0.5,a2 = 0.5,d = 1,Q = 1.4,βi = 1.0,and βe = 0.5 |
A heat transfer analysis is performed for the peristaltic transport of an electrically conducting fluid under the influence of the applied uniform magnetic field. The generalized Ohm’s law is used to consider the Hall and ion slip effects. Viscous and Ohmic heating effects are also taken into account. The exact solutions of the governing problems are constructed with the wave reference frame. The main findings obtained from the present article may be summarized as follows:
(i) The maximum pressure,which is required to produce zero flow rate,decreases when βe and βi increase while increases when Ha increases.
(ii) When βe and βi increase and Ha decreases,the frictional forces Fλs (s = 1,2) increase first,and then decrease after a certain value of the flow rate Q.
(iii) All Q0,Q h1,and Qh2 increase when βe and βi are increased or Ha is decreased.
(iv) The magnitude of the pressure gradient dp/dx decreases when βe and βi increase while increases when Ha increases.
(v) For small Ha,the amplitude of the velocity u slightly increases when βe increases. However,for large Ha,the amplitude of the velocity u greatly increases when βe increases. Similar effects on u are noticed when the ion slip parameter βi increases.
(vi) The temperature θ decreases when βe and βi increase,and increases when Ha and Br increase. These observations are also true for the absolute value of the heat transfer coefficient Z .
(vii) For large Ha,the effects of βe and βi are more pronounced on the pressure rise ∆Pλ , the frictional forces Fλs (s = 1,2),the pressure gradient dp/dx,the velocity u,the temperature θ,and the heat transfer coefficient Z at the upper wall. However,the critical value varies at the sharp rate for small Ha.
(viii) The size of the trapped bolus increases when βe and βi increase,and decreases when Ha increases.
| [1] | Latham, T. W. Fluid Motion in a Peristaltic Pump, M. Sc. dissertation, Massachusetts Institute of Technology, Massachusetts (1966) |
| [2] | Shapiro, A. H. Pumping and retrograde diffusion in peristaltic waves. Proceedings of the Workshop in Ureteral Reflux in Children, Washington, D.C., 109-126 (1967) |
| [3] | Afifi, N. A. S. and Gad, N. S. Interaction of peristaltic flow with pulsatile magnto-fluid through a porous medium. Acta Mechanica, 149, 229-237 (2001) |
| [4] | El-Shehawey, E. F. and Husseny, S. Z. A. Peristaltic transport of a magneto-fluid with porous boundaries. Applied Mathematics and Computation, 129, 421-440 (2002) |
| [5] | Mekheimer, K. S. Peristaltic flow of blood under the effect of magnetic field in a non-uniform channel. Applied Mathematics and Computation, 153, 763-777 (2004) |
| [6] | Hayat, T. and Ali, N. Peristaltically induced motion of MHD third grade fluid in a deformable tube. Physics Letters A, 370, 225-239 (2006) |
| [7] | Ali, N., Hussain, Q., Hayat, T., and Asghar, S. Slip effects on the peristaltic transport of MHD fluid with variable viscosity. Physics Letters A, 372, 1477-1489 (2008) |
| [8] | Shahed, M. E. and Haroun, M. H. Peristaltic transport of Johson-Segalman fluid under effect of a magnetic field. Mathematical Problems in Engineering, 6, 663-667 (2005) |
| [9] | Ebaid, A. Effects of magnetic field and wall ion slip conditions on the peristaltic transport of a Newtonian fluid in an asymmetric channel. Physics Letters A, 372, 4493-4499 (2008) |
| [10] | Wang, Y., Ali, N., Hayat, T., and Oberlack, M. Peristaltic motion of a magnetohydrodynamic micropolar fluid in a tube. Applied Mathematical Modelling, 35, 3737-3750 (2011) |
| [11] | Mekheimer, K. S., Komy, S. R., and Abdelsalam, S. I. Simultaneous effects of magnetic field and space porosity on compressible Maxwell fluid transport induced by a surface acoustic wave in a microchannel. Chinese Physics B, 22, 124702 (2013) |
| [12] | Ogulu, A. Effect of heat generation on low Reynolds number fluid and mass transport in a single lymphatic blood vessel with uniform magnetic field. International Communications in Heat and Mass Transfer, 33, 790-799 (2006) |
| [13] | Mekheimer, K. S. and Abd-Elmaboud, Y. The influence of heat transfer and magnetic field on peristaltic transport of a Newtonian fluid in a vertical annulus: application of an endoscope. Physics Letters A, 372, 1657-1665 (2008) |
| [14] | Vajravelu, K., Radhakrishnamacharya, G., and Radhakrishnamurty, V. Peristaltic flow and heat transfer in a vertical porous annulus with long wave approximation. International Journal of Nonlinear Mechanics, 42, 754-759 (2007) |
| [15] | Srinivas, S. and Kothandapani, M. Peristaltic transport in an asymmetric channel with heat transfer-a note. International Communications in Heat and Mass Transfer, 35, 514-522 (2008) |
| [16] | Nadeem, S. and Akbar, N. S. Effects of heat transfer on the peristaltic transport of MHD Newto- nian fluid with variable viscosity: application of Adomian decomposition method. Communications in Nonlinear Science and Numerical Simulation, 14, 3844-3855 (2009) |
| [17] | Radhakrishnamacharya, G. and Srinivasulu, C. Influence of wall properties on peristaltic transport with heat transfer. Comptes Rendus Mecanique, 335, 369-373 (2007) |
| [18] | Hayat, T., Abbasi, F. M., and Obaidat, S. Peristaltic motion with Soret and Dufour effects. Magnetohydrodynamics, 47, 295-302 (2011) |
| [19] | Hayat, T., Hina, S., Hendi, A. A., and Asghar, S. Effect of wall properties on the peristaltic flow of a third grade fluid in a curved channel with heat and mass transfer. International Journal of Heat and Mass Transfer, 54, 5126-5136 (2011) |
| [20] | Hayat, T., Noreen, S., Alhothuali, M. S., Asghar, S., and Alhomaidan, A. Peristaltic flow under the effects of an induced magnetic field and heat and mass transfer. International Journal of Heat and Mass Transfer, 55, 443-452 (2012) |
| [21] | Abd-Elmaboud, Y., Mekheimer, K. S., and Abdellartif, A. Thermal properties of couple-stress fluid flow in an asymmetric channel with peristalsis. Journal of Heat Transfer, 135, 044502 (2013) |
| [22] | Cramer, K. and Pai, S. I. Magnetofluid Dynamics for Engineers and Applied Physicists, Scripta Publishing Company, Texas (1973) |
| [23] | Hayat, T., Ali, N., and Asghar, S. Hall effects on peristaltic flow of a Maxwell fluid in a porous medium. Physics Letters A, 363, 397-403 (2007) |
| [24] | Abo-Eldahab, E. M., Barakat, E. I., and Nowar, K. I. Effects of Hall and ion-slip currents on peristaltic transport of a couple stress fluid. International Journal of Applied Mathematics and Physics, 2, 145-157 (2010) |
| [25] | Abo-Eldahab, E. M., Barakat, E. I., and Nowar, K. I. Hall currents and ion-slip effects on the MHD peristaltic transport. International Journal of Applied Mathematics and Physics, 2, 113-123 (2010) |
| [26] | Haroun, M. H. A mathematical study of Hall effects on peristaltic transport of hydromagnetic flow through a porous medium. Journal of Porous Media, 10, 687-700 (2007) |
| [27] | Mekheimer, K. S., Salem, A. M., and Zaher, A. Z. Peristatcally induced MHD ion slip flow in a porous medium due to a surface acoustic wavy wall. Journal of the Egyptian Mathematical Society, 22, 143-151 (2014) |
| [28] | Mekheimer, K. S. and El-Kot, M. A. Influence of magnetic field and Hall currents on blood flow through a stenotic artery. Applied Mathematics and Mechanics (English Edition), 29, 1093-1104 (2008) DOI 10.1007/s10483-008-0813-x |
| [29] | Cowling, T. G. Magnetohydrodynamics, Interscience Publishers, New York and London (1957) |
 2014, Vol. 35
2014, Vol. 35

























