Shanghai University
Article Information
- Xiang-wu PENG, Xing-ming GUO, Liang LIU, Bing-jie WU. 2015.
- Scale effects on nonlocal buckling analysis of bilayer composite plates under non-uniform uniaxial loads
- Appl. Math. Mech. -Engl. Ed., 36(1): 1-10
- http://dx.doi.org/10.1007/s10483-015-1900-7
Article History
- Received 2014-6-13;
- in final form 2014-10-31
Since Iijima[1] first discovered carbon nanotubes,many nanostructures have been manufactured by the experimental means,such as nanobeams[2],nanorings[3],and nanoplates[4]. Graphene is an important two-dimensional carbon nanostructure because nanotubes and nanorings can be viewed as deformed graphene sheets. Therefore,analysis of graphene sheets is a fundamental issue in the study of nanomaterials. In addition,these nano-scale structures can be used to create some special structures with certain functions. They are found to possess extraordinary mechanical,electrical,and thermal properties,compared with traditional structural materials. Moreover,it requires accurate characterization of their mechanical elements[5, 6] to develop nano-scale instruments and devices for nano-electromechanical systems (NEMS) in modern technology. The systems consisting of thin films on a compliant substrate occupy an important position in NEMS. In the production process of composite micro-nanoelectronics components (e.g.,film,substrate,and package),NEMS fails because of the residual thermal stress or the dislocation strain,which is caused by the mismatch of the thermal and mechanical parameters under the heating and cooling of the molding process.
The classical continuum mechanics methods[7] have been used to analyze the mechanics of micro-nano materials. Yakobson et al.[8] found that the continuum mechanics model was valid in compression,bending,and torsion problem of carbon nanotubes by comparing with the method of molecular dynamics. Ru[9, 10] studied the buckling problem of double-wall carbon nanotubes under compression,where double-wall carbon nanotubes were modeled as doublewall cylindrical shells,and the interaction between the shells was described by the van der Waals force. However,more research on scale effects showed that it was necessary to study more accurate mechanic for micro- and nano-structures[11, 12, 13]. Based on the nonlocal theory[14], Pradhan andMurmu[15] studied the buckling analysis of single-layered graphene sheet embedded in an elastic medium,while Assadi and Farshi[16] investigated the stability analysis of graphene based laminated composite sheets under non-uniform inplane loading.
Inspired by the previous studies,this paper presents the nonlocal buckling problem of the bilayer composite plates,where two plates are isotropic with different material parameters,and the adhesive layer between the two plates is modeled as the Winkler elastic medium[17]. Effects of the nonlocal parameter,the non-dimensional Winkler parameter,the thickness ratio,the ratio of Young’s moduli,and the aspect ratio are considered based on the buckling theory and nonlocal elastic theory. Generally,the nonlocal effects are of importance when higher buckling modes occur. In the classical elastic theory,we find that higher buckling modes can appear in the present model under a certain circumstance. Thus,the present model shows that the nonlocal effects are significant. In addition,the multilayer graphene sheets can be regarded as the present model,where the top plate is the top single graphene while the bottom plate is consisting of the remaining multilayer graphene sheets. 2 Model and buckling analysis 2.1 Nonlocal theory for plate
In classical elasticity theories,the constitutive relationships are considered as that the stress field at a point x0 only depends on the strain field at that point. Apart from this,the stress field at that point also depends on the strains at all the other points in the domain of that point in the nonlocal elasticity theory. According to Eringen[18],it is attributed to the atomic theory of lattice dynamics and experimental observations on phonon dispersion. Therefore,the constitutive relationships for nonlocal elasticity theory can be written as
In (1),σij,εmn,and Cijmn are the stress,the strain,and the elastic moduli tensors,respectively,while the Kernel function

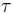 is
a material constant that depends on the internal characteristic length a and the external characteristic length
is
a material constant that depends on the internal characteristic length a and the external characteristic length 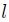 in the form of e0a/
in the form of e0a/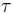 with e0 being a determined material constant adjusting
to the experimental results or the previous validated models.
with e0 being a determined material constant adjusting
to the experimental results or the previous validated models.
Unfortunately,it is difficult to solve the integral problem in (1). Eringen[19] reduced it to an equivalent differential form for linear isotropic elastic bodies as follows:
For the 2D thin plate,(2) can be expressed as
where E,G,and μ are Young’s modulus,shear modulus,and Poisson’s ratio,respectively,and

Based on the small deflection buckling theory of plate[7, 20, 21, 22],the displacement field of the Kirchhoff plate can be expressed as
where u,v,and w denote the displacements of the point in the middle plane along the x-,y-, and z-directions,respectively. The strains associated with the displacement field (4) areThe stress resultants are defined by
Applying the minimum total potential energy and omitting the body forces,we obtain the equilibrium equations as follows:
Using (3),(5),and (6),we have the nonlocal constitutive relationships in terms of displacements as follows:
where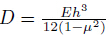 is the flexural rigidity.
is the flexural rigidity.
Therefore,we can get the governing equation for buckling of plate via the nonlocal elastic theory as follows:
2.2 Buckling analysis of modelConsider that the xy-plane is located at the interface of the top layer “1” (with thickness “h1”) and the bottom layer “2” (with thickness “h2”),having different material elastic moduli and Poisson ratios Ei and vi (i=1,2). The adhesive layer between the top plate and the bottom plate is modeled as the Winkler elastic medium with an elastic constant K. The only external loads are also modeled as different loads N1 and N2 applying on the top plate and the bottom plate,respectively,along the X-axis,as shown in Fig. 1.
 |
| Fig. 1. Bilayer composite plates and mechanical model |
Based on the nonlocal theory of plate aforementioned,the nonlocal buckling equations for bilayer composite plates are expressed as follows:
where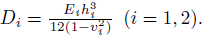
With the assumption of simplified supported boundary conditions on all the sides of each plate,by employing the well-known Navier series solution,the buckling deflection of each plate can be written as follows:
Substituting (11) into (10),we obtain the coupled buckling system of equations in the following form: where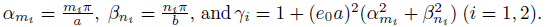
Actually,with the existence of the adhesive layer,we only consider that bilayer plates buckle without debonding. Thus,the only acceptable buckling wavenumbers of each plate should be the same,i.e.,m1 = m2 = m and N1 = N2 = n.
Therefore,(12) can be simplified to result in the following relationships:
where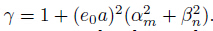
Now,we consider the two-layer plates under non-uniform uniaxial compression,i.e.,assume N1 ≠ 0 and N2 = 0. With the equation wr = W2mn/W1mn,(13) can lead to
2.3 Buckling mode analysis for classic elastic theoryNonlocal effects are considerable when higher buckling modes occur. Therefore,whether higher buckling modes occur or not,we analyse the nonlocal effects in the classical elastic theory,i.e.,(e0a)2 = 0. Then,γ= 1,and we have
Derived from (16),wr satisfies 0 < wr0 < 1 (i.e.,0 < w2mn < w1mn). We note that the deformation deflection of the top and bottom plates is in the same size,and the maximum deflection amplitude of the top plate is larger than that of the bottom plate. Moreover,we should note that the buckling wavenumber n is 1 along the direction of width b.
(i) Case 1 When the Winkler elastic coefficient makes the top and bottom plates deform consistently,or the flexural rigidity of the bottom plate is so small that it can be ignored (i.e., K → +∞ or D2 → 0),(16) becomes wr0 = 1 (i.e.,w1mn = w2mn),and therefore w1 = w2.(15) can be written as
The minimization of N10 with respect to the wavenumber m requires that Substituting (17) into (18) yields(ii) Case 2 When the Winkler elastic coefficient is so small that it can be ignored as complete debonding (i.e.,K → 0),(16) becomes wr0 = 0 (i.e.,w2mn = 0),and therefore w2 = 0. That means the bottom plate does not bend under an infinitely small force. From (15),we have
Substitution of (20) into (18) also can yield (19). (20) can be acceptable since we only consider the small deflection problem under N1 ≠ 0 and N2 = 0.
(iii) Case 3 When the flexural rigidity of the bottom plate is larger than that of the top plate (i.e.,D2 → +∞),(16) becomes wr0 = 0 (i.e.,w2mn = 0),and therefore w2 = 0. That is, the bottom plate can be considered as a rigid body. Then,(15) can be derived to
Substituting (21) into (19) yields
In such a case,it is found that the critical buckling wavenumber is dependent not only on the aspect ratio,but also upon the Winkler elastic coefficient and the flexural rigidity of the top plate,and the higher buckling modes may appear when the bottom plate does not bend or buckle under the external force because of the higher flexural rigidity. 3 Numerical examples and discussion
For brevity and generality,we introduce the non-dimensional parameters as follows:
where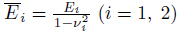 ,and the critical buckling load ratio is
,and the critical buckling load ratio is 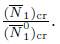 3.1 Effect of nonlocal parameter (e0a)2
3.1 Effect of nonlocal parameter (e0a)2To illustrate the nonlocal effects on the buckling problem of bilayer composite plates,curves are plotted for the critical buckling load ratio against the nonlocal parameter,where the aspect ratio is unity,and the non-dimensional Winkler parameter is 104,while the flexural rigidity ratios are taken as D2/D1 = 1 and 100 in Figs. 2(a) and 2(b),respectively. It is seen that the nonlocal effects are very little from Fig. 2(a),while the nonlocal effects are distinguished from γ = 1 + (e0a)2 (αm2+ βn2),the flexural rigidity of plate is smaller after the nonlocal parameter is considered,i.e.,D → D/γ. Thus,the critical buckling load will be smaller,which means that the systems will buckle easily under the nonlocal elastic theory. As mentioned previously,in the absence of the nonlocal parameter,the buckling mode is (1,1) with the flexural rigidity ratio 1,while the buckling mode is (10,1) with the flexural rigidity ratio 100. is larger with the higher buckling modes. Hence,the flexural rigidity is smaller,which leads the critical buckling load to be smaller,and also the nonlocal effects are notable.
 |
| Fig. 2. Effect of nonlocal parameter (e0a)2 on critical buckling load ratio |
The adhesive layer between the two plates is an elastic medium,which is modeled as the Winkler elastic medium. Here,the aspect ratio is unity,and the flexural rigidity ratios are fixed as 1 and 100 for comparison. Curves are plotted for the critical buckling load ratio against the non-dimensional Winkler parameter. The nonlocal parameters almost have no impact on critical buckling load ratio with the increase of the non-dimensional Winkler parameter,as shown in Fig. 3(a),while the influence of the nonlocal parameters on critical buckling load ratio is significant with the increase of the non-dimensional Winkler parameter (see Fig. 3(b)).
 |
| Fig. 3. Effect of non-dimensional Winkler parameter K on critical buckling load ratio |
As mentioned previously,the nonlocal effects are significant for higher buckling modes. In
the absence of the nonlocal parameter,the fixed aspect ratio a/b = 1 and the fixed flexural rigidity ratio D2/D1 = 1 both lead to the buckling mode (m,n) = (1,1) whatever the
non-dimensional Winkler parameter is. In that case,the nonlocal buckling load almost equals
the classical buckling load,and hence the nonlocal effects can be ignored. However,based on
Case 3,higher buckling modes may appear when the bottom plate can be regarded as a rigid
body,and the critical buckling wavenumber depends on the non-dimensional Winkler parameter. The wavenumber increases with the increase of the non-dimensional Winkler parameter.
Higher buckling modes occur,and hence the critical nonlocal buckling loads become smaller
dramatically. It is worth noting that the wavenumber does not increase infinitely when the
non-dimensional Winkler parameter increases infinitely.
3.3 Effects of thickness ratio  and ratio of Young’s moduli
and ratio of Young’s moduli 
This paper deals with the buckling problem of bilayer composite plates via the nonlocal
elastic theory. Each isotropic plate is composed of a material different from the others. They
have different Young’s moduli and geometric sizes. Therefore,the influence of thickness ratio
and Young’s moduli on nonlocal buckling problem should be considered,and the flexural rigidity
ratio is composed as  . The parameters are fixed as the ratio of Young’s modulus
is 0.1 in Fig. 4(a),and the thickness ratio is unity in Fig. 4(b),while the aspect ratio is unity,
and the non-dimensional Winkler parameter is 104. The curves are plotted for the critical
buckling load ratio.
. The parameters are fixed as the ratio of Young’s modulus
is 0.1 in Fig. 4(a),and the thickness ratio is unity in Fig. 4(b),while the aspect ratio is unity,
and the non-dimensional Winkler parameter is 104. The curves are plotted for the critical
buckling load ratio.
 |
| Fig. 4. Effects of thickness ratio h2/h1 and ratio of Young’s moduli E2/E1 on critical buckling load ratio |
From the figures,it can be seen that the critical buckling ratio decreases linearly from a steady value to another steady value when the thickness ratio (or the ratio of Young’s moduli) increases. The nonlocal effects are obvious. The bottom plate can be regard as a rigid body when the thickness ratio (or the ratio of Young’s moduli) reaches a certain value. In that circumstance,higher buckling modes may occur,which depends on the non-dimensionalWinkler parameter. 3.4 Effect of aspect ratio a/b
Based on the literature[21],the buckling wavenumber increases with the aspect ratio on the buckling analysis of classic single plate under uniaxial compression. In addition,the nonlocal effects are notable when higher buckling modes appear according to the previous analysis. Thus, we should consider the impact of aspect ratio under the nonlocal theory. To compare with the results of the classical elastic theory,curves are plotted for the critical buckling load ratio for two circumstances where the flexural rigidity ratio is 1 in Fig. 5(a),and the flexural rigidity ratio is 100 in Fig. 5(b),both having a non-dimensional Winkler parameter 104.
 |
| Fig. 5. Effect of aspect ratio a/b on critical buckling load ratio |
Figure 5 shows that the critical buckling load ratio becomes stable with the increase of the
aspect ratio,although the nonlocal effects are considerable by Fig. 5(b). As aforementioned,the
higher buckling modes appear when the bottom plate does not bend or buckle. Therefore,the
nonlocal effects occur so that the critical nonlocal buckling loads are smaller than the critical
classic buckling loads obviously. However,Fig. 5 shows that the nonlocal effects are pronounced
when the aspect ratio is small enough. In fact,the critical buckling wavenumbers must be
positive integers under physical boundary effects and are equal to 1 at least,although the
wavenumber depends on the aspect ratio. From  ,the flexural rigidity
D/γ decreases in the nonlocal theory,and hence the critical nonlocal buckling loads also are
smaller than those based on the classical elastic theory. The waves of curves in Fig. 5(b) can
be explained as that the buckling modes based on the nonlocal elastic theory are not the same
as those of classical elastic theory.
4 Conclusions
,the flexural rigidity
D/γ decreases in the nonlocal theory,and hence the critical nonlocal buckling loads also are
smaller than those based on the classical elastic theory. The waves of curves in Fig. 5(b) can
be explained as that the buckling modes based on the nonlocal elastic theory are not the same
as those of classical elastic theory.
4 Conclusions
Based on the nonlocal elastic theory,the present paper deals with the scale effects on the buckling problem of bilayer composite plates under a non-uniform uniaxial load. Each plate is isotropic,and the adhesive between the two plates is modeled as the Winkler elastic medium. The material parameters and geometric sizes of the plate are different from each other. Effects of the nonlocal parameter,the Winkler non-dimensional parameter,the thickness ratio,the ratio of Young’s moduli,and the aspect ratio are investigated. Numerical results reach several conclusions as follows. Nonlocal effects are pronounced when higher buckling modes appear or the aspect ratio is small enough. Higher buckling modes may appear when the bottom plate does not bend or buckle. The buckling wavenumber depends not only on the aspect ratio but also on the Winkler elastic coefficient and the flexural rigidity of the top plate. The thickness ratio and the ratio of Young’s moduli determine whether the bottom plate can be considered as a rigid body. The nonlocal effects can be ignored when the aspect ratio is larger in spite of the presence of higher buckling modes.
| [1] | Iijima, S. Helical microtubules of graphitic carbon. nature, 354, 56-58 (1991) |
| [2] | Lu, P., Lee, H. P., Lu, C., and Zhang, P. Q. Dynamic properties of flexural beams using a nonlocal elasticity model. Journal of Applied Physics, 99, 073510 (2006) |
| [3] | Wang, C. M. and Duan, W. H. Free vibration of nanorings/arches based on nonlocal elasticity. Journal of Applied Physics, 104, 014303 (2008) |
| [4] | Duan, W. H. and Wang, C. M. Exact solutions for axisymmetric bending of micro/nanoscale circular plates based on nonlocal plate theory. Nanotechnology, 18(38), 385704 (2007) |
| [5] | Gupta, A., Akin, D., and Bashir, R. Detection of bacterial cells and antibodies using surface micromachined thin silicon cantilever resonators. Journal of Vacuum Science & Technology B, 22(6), 2785-2791 (2004) |
| [6] | Li, C., Thostenson, E. T., and Chou, T. W. Sensors and actuators based on carbon nanotubes and their composites: a review. Composites Science and Technology, 68(6), 1227-1249 (2008) |
| [7] | Timoshenko, S. P. and Goodier, J. N. Theory of Elasticity, McGraw-Hill Publishing Company, New York (1970) |
| [8] | Yakobson, B. I., Brabec, C. J., and Bernholc, J. Nanomechanics of carbon tubes: instabilities beyond linear response. Physcial Review Letters, 76, 2511-2514 (1996) |
| [9] | Ru, C. Q. Axially compressed buckling of a double-walled carbon nanotube embedded in an elastic medium. Journal of the Mechanics and Physics of Solids, 49, 1265-1279 (2001) |
| [10] | Ru, C. Q. Effect of van de Waals forces on axial buckling of a double-walled carbon nanotube. Journal of Applied Physics, 87, 7227-7231 (2000) |
| [11] | Ansari, R., Rajabiehfard, R., and Arash, B. Nonlocal finite element model for vibrations of em-bedded multilayered graphene sheets. Computational Materials Science, 49, 831-838 (2010) |
| [12] | Arash, B. and Wang, Q. A review on the application of nonlocal elastic models in modeling of carbon nanotubes and graphenes. Computational Materials Science, 51, 303-313 (2012) |
| [13] | Wang, C. M., Zhang, Y. Y., Ramesh, S. S., and Kitipornchai, S. Buckling analysis of micro-and nano-rods/tubes based on nonlocal Timoshenko beam theory. Journal of Physics D: Applied Physics, 39(17), 3904-3909 (2006) |
| [14] | Erigen, A. C. Nonlocal Continuum Field Theories, Springer, New York (2001) |
| [15] | Pradhan, S. C. andMurmu, T. Small scale effect on the buckling analysis of single-layered graphene sheet embedded in an elastic medium based on nonlocal plate theory. Physica E, 42, 1293-1301 (2010) |
| [16] | Assadi, A. and Farshi, B. Stability analysis of graphene based laminated composite sheets under non-uniform inplane loading by nonlocal elasticity. Applied Mathematical Modelling, 35, 4541-4549 (2011) |
| [17] | Murmu, T., Sienz, J., Adhikari, S., and Arnold, C. Nonlocal buckling of double nanoplate systems under biaxial compression. Composites Part B: Engineering, 44, 84-94 (2013) |
| [18] | Erigen, A. C. Nonlocal polar elastic continua. International Journal of Engineering Science, 10, 1-16 (1972) |
| [19] | Eringen, A. C. On differential equations of nonlocal elasticity and solutions of screw dislocation and surface waves. Journal of Applied Physics, 54, 4703-4710 (1983) |
| [20] | Wu, L. Y. Stability Theory of Plates and Shells (in Chinese), Huazhong University of Science & Technology Press, Wuhan (1996) |
| [21] | Huang, Y. and He, F. S. Beams, Plates and Shells on Elastic Foundation (in Chinese), Science Press, Beijing (2005) |
| [22] | Reddy, J. N. Nonlocal nonlinear formulations for bending of classical and shear deformation theories of beams and plates. International Journal of Engineering Science, 48, 1507-1518 (2010) |
 2015, Vol. 36
2015, Vol. 36
























