Shanghai University
Article Information
- A. K. VASHISHTH, H. SUKHIJA. 2015.
- Reflection and transmission of plane waves from fluid-piezothermoelastic solid interface
- Appl. Math. Mech. -Engl. Ed., 36(1): 11-36
- http://dx.doi.org/10.1007/s10483-015-1892-9
Article History
- Received 2014-2-1;
- in final form 2014-5-15
Smart materials are different from the usual materials and can sense their environment and respond. Their properties can be significantly altered in a controlled fashion by external stimuli such as stress,temperature,electric,and magnetic fields. Such characteristics enable technological applications across a wide range of sectors including electronics,construction, transportation,agriculture,food and packaging,health care,space,defence,etc. A lot of studies have been done in this field,and details are sketched in many texts[1, 2, 3, 4, 5, 6].
The problems of reflection and refraction of elastic waves have been discussed by many authors. Knott[7] discussed the problem of reflection and refraction of elastic waves with seismological applications. Crampin and Taylor[8] studied surface wave propagation in anisotropic media. Crampin[9] calculated the particle motion of surface waves propagating in particular symmetry directions in anisotropic media. A full account of reflection and refraction of elastic waves were given by Achenbach[10]. Pal and Chattopadhyay[11] studied the reflection phenomenon of plane waves at a free boundary in a pre-stressed elastic half-space. The three-dimensional reflection and transmission coefficients for plane waves in isotropic elastic media were derived by Borejko[12],where an extensive survey of literature pertinent to the problem of reflection and transmission of plane waves was also given. Ogden and Sotirropoulos[13, 14] investigated the problems of reflection in both incompressible and compressible elasticity. Chattopadhyay and Rogerson[15] studied reflection of plane waves at an incrementally traction-free boundary of a half-space composed of a linearly incompressible elastic material. Chattopadhyay[16] studied the wave reflection in a triclinic crystalline medium,and Deschamps[17] studied the problem of reflection and refraction of the plane wave.
The coupled theory of thermoelasticity was extended by Lord and Shulman[18] and Green and Lindsay[19] by incorporating the thermal relaxation time in constitutive relations. Some problems on reflection in thermoelastic solid have been discussed by Deresiewicz[20],Sinha and Sinha[21],and Singh[22]. Sinha and Elsibai[23] discussed the reflection of thermoelastic waves at a free surface of solid half-space with two kinds of relaxation time. Abd-Alla and Al-Dawy[24] investigated the reflection phenomenon of the shear vertical (SV) waves in a generalized thermoelastic medium. Sharma et al.[25] studied the reflection of generalized thermoelastic waves from the stress free as well as the rigidly fixed thermally insulated or isothermal boundary of a thermoelastic solid half-space by considering the case of P and SV incidence waves. Deschamps and Cheng[26] studied the reflection problem in a liquid-thermoviscoelastic solid interface.
A number of problems,which are related to the phenomenon of reflection and refraction of plane waves for piezoelectric materials,can be found in the literature[2, 27]. In designing acoustic transducers,knowledge and control of the reflection and transmission of ultrasonic waves at the boundary between piezoelectric materials and water are important,which,in most of cases,are piezoelectric ceramics for use in under water imaging[28, 29]. Nayfeh and Chien[30, 31] derived the analytical expressions for the reflected and transmitted amplitude ratios for the fluid loaded piezoelectric plate and fluid loaded piezoelectric half-space in order to study the influence of piezoelectricity on such waves.
A thermo-piezoelectricity theory was first proposed by Mindlin[32],who later derived the governing equations of a thermo-piezoelectric plate[33]. The physical laws for the thermopiezoelectric materials were explored by Nowacki[34]. Chandrasekharaiah[35] has generalized Mindlin’s theory of thermo-piezoelectricity to take into account the finite speed of propagation of thermal disturbances. The effect of anisotropy on wave propagation in piezo-thermoelastic media has also been analyzed in some recent studies[36, 37, 38]. Sharma[39] solved the mathematical model to calculate the complex phase velocities of four attenuated waves. Sharma et al.[40] discussed the reflection of piezo-thermoelastic waves from the charge and stress free boundary of a transversely isotropic half-space. The theoretical and experiemental studies of reflection and refraction of piezo-thermoelastic waves are of considerable interest in many engineering and industrial applications such as sensors,actuators,intelligent structures,radio,computer technology,and ultrasonic. A number of problems of reflection and refraction at fluid-solid interfaces have been undertaken by many authors[41, 42, 43],but the problem of reflection and refraction at fluid-piezothermoelastic interfaces is still left.
In this paper,the problem of reflection and transmission of plane waves from a fluid-piezothermoelastic solid interface is considered. A piezo-thermoelastic half-space (PTHS),having 6mm symmetry,loaded with fluid half-space (FHS),is considered,and the expressions for the amplitude ratios and the energy ratios corresponding to reflected and transmitted waves are derived analytically using boundary conditions. Some reduced cases are discussed,and the effects of the angle of incidence,the frequency,the specific heat,the relaxation time,and the thermal conductivity on the reflected and transmitted energy ratios are observed for a particular model of cadmium selenide (CdSe) and water. Some special cases of interest are also discussed. 2 Basic equations
Consider a homogeneous,anisotropic,thermally conducting,piezoelectric elastic medium of the density ρ at a uniform temperature To in an undisturbed state. The basic equations are as follows. The strain-displacement relations are
the stress-strain-temperature and electric field relations are the equations of motion are the heat conduction equation is and the Gauss equation is where σij are the stress tensors,cijkl are the elastic constants,ekl are the strain tensors, ui are the displacement components in the medium,ηijkijk and εij represent the piezoelectric constants and the dielectric permittivity coefficients,respectively,βij are the thermoelastic coupling tensors,and Kij correspond to the thermal conductivities. ρ and Ce are the density and the specific heat at constant strain,respectively. The Lord and Shulman (LS) theory involves the thermal relaxation time τo,which represents the time lag needed to establish steady state heat conduction in an element of volume when a temperature gradient is suddenly imposed on that element. The Green and Lindsay (GL) theory involves the thermal relaxation time τo and τ1 such that τo>τ1>0. pi are the pyroelectric constants,Ek are the components of the electric field vector,and φ represents the electric potential. The convention of repeated index for summation is adopted. The dot and comma notations denote (partial) differentiation with respect to time and space,respectively. The symbols δ1k and δ2k denote the Kronecker delta. Here,κ=1 for the LS theory and κ = 2 for the GL theory. The parameters in Eqs. (1)-(5) are assumed to satisfy the following conditions:(i) The thermal conductivity Kij and the dielectric permittivity εij are symmetric and positive definite.
(ii) The pyroelectric coefficients are positive.
(iii) The piezoelectric modulus tensors ηijk are symmetric in indices j and k.
(iv) The thermoelastic coupling tensors βij are non-singular.
(v) The specific heat Ce at constant strain is positive.
(vi) The isothermal linear elastic coefficients are positive definite in the sense that cijkleijekl > 0.
The constitutive equations of piezo-thermoelastic material in the x1x3-plane in the absence of body forces and free charge density are
where

The harmonic plane waves,propagating in the x1x3-plane at a given angular frequency (ω), can be expressed as
where q is the unknown slowness parameter,and c is the apparent phase velocity. U,A,B, and C are the amplitudes associated with the harmonic wave. Then,Eqs. (3)-(5),along with Eqs. (6) and (7),reduce to a system where S = [U,A,B,C]T,and Γ is a 4×4 matrix whose elements are listed in Appendix A. This system is consistent ifThe desired expressions of the coefficients Tj (j = 1,2,· · · ,5) are given in Appendix B. q1,q2,q3,and q4 correspond to the roots of this equation whose imaginary parts are positive, and q5,q6,q7,and q8 denote those whose imaginary parts are negative. Here,q4 corresponds to the electric potential component wave mode (PE1),and q1,q2,and q3 correspond to the propagating quasi P (qP) mode,quasi S (qS) mode,and quasi T (qT) mode of wave propagation, respectively. For each qi (i = 1,2,· · · ,8),the corresponding eigen vectors Ui,Ai,Bi,and Ci can be written as
where and c(Γij)qi denotes the cofactor of Γij to the eigen value qi. The amplitudes (U,A,B,and C) of the plane harmonic waves decrease as these waves progress in a piezo-thermoelastic medium. The amplitudes of the plane harmonic waves propagating in a piezo-thermoelastic medium also depend on the frequency. The formal solution for the mechanical displacement and the electric potential becomesThe dynamical equations for the fluid are
where σijf and uif are the stress tensors and displacements in the FHS,respectively,and ρf and λf are the density and the bulk modulus of the fluid,respectively.The normal stresses are related to the dilatation by the relation
The solution to Eq. (14) can be expressed as where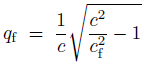 is the unknown slowness parameter,Uf and Af are the associated
amplitudes,and cf is the longitudinal wave velocity in the fluid medium.
3 Reflection and transmission coefficients
3.1 Amplitude ratios
is the unknown slowness parameter,Uf and Af are the associated
amplitudes,and cf is the longitudinal wave velocity in the fluid medium.
3 Reflection and transmission coefficients
3.1 Amplitude ratiosConsider a PTHS,having 6mm symmetry,loaded with the FHS. The PTHS occupies the region x3 ≥ 0,and the FHS occupies the region x3 ≤ 0,as shown in Fig. 1. A plane wave, making an angle θ with the x3-axis,becomes incident at the interface. This wave results in one reflected wave in the FHS and four transmitted modes in the PTHS. The transmitted wave modes are represented by qP,qS,qT,and the fourth mode PE1 corresponds to the electric potential wave mode. The formal solutions for the mechanical displacements,the temperature, the electric potential,the stress components,and the electric displacements in a PTHS are
 |
| Fig. 1. Geometry of problem |
The coefficients D1i,D2i,and D4i have been calculated and are given in Appendix C. Substituting Eq. (16) into Eq. (14) gives the displacements of incident and reflected waves as
where p = 1 corresponds to the incident wave,p = 2 corresponds to the reflected wave,and

Accordingly,the normal stress becomes
The boundary conditions at the interface x3 = 0 are as follows:(i) The mechanical boundary conditions are
(ii) The electrical boundary conditions are
(iii) The thermal boundary conditions are
Equations (17)-(19) and the above boundary conditions result in a non-homogeneous system
where


At the interface x3 = 0,the distribution of energy between different reflected and transmitted waves across a surface element of unit area is considered. Following Ikeda[4],Scott[44],and Kuang and Yuan[45],the normal acoustic flux P in a piezo-thermoelastic solid is
The average energy fluxes of the incident and reflected waves are

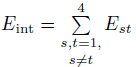 is the resultant interaction energy between the transmitted waves.
4 Reduced cases
is the resultant interaction energy between the transmitted waves.
4 Reduced casesReflection and transmission of plane waves are studied for the following types of the fluidPTHS interface:
(i) Open and isothermal interface
By invoking the stress free,isothermal,and charge free boundary conditions (20a)-(20c), (20d),and (20f) at the surface x3 = 0,we obtain a non-homogeneous system
where


By solving this system,we obtain the values of transmitted and reflected amplitude ratios. Then,using these values of amplitude ratios and equations from (23)-(28),we can calculate the energy ratios for different waves.
(ii) Closed and isothermal interface
Upon invoking the stress free,isothermal,and electrically shorted boundary conditions (20a)-(20c),(20e),and (20f) at the surface x3 = 0,we obtain a non-homogeneous system
where


(iii) Open and adiabatic interface
Upon invoking the stress free,adiabatic,and charge free boundary conditions (20a)-(20c), (20d),and (20g) at the surface x3 = 0,we obtain a non-homogeneous system
where


(iv) Closed and adiabatic interface
Upon invoking the stress free,adiabatic,and electrically shorted boundary conditions (20a)-(20c),(20e),and (20g) at the surface x3 = 0,we obtain a non-homogeneous system
where


(v) Fluid-piezoelectric solid interface
If we set β11 = β33 = p3 = K11 = K33 = Ce = 0,the motion corresponding to the thermal wave decouples from rest of motion. The Christoffel equation for the piezoelectric material now becomes
where T1P,T2P ,T3P ,and T4P are given in Appendix D. q1P,q2P,and q3P correspond to the roots of this equation whose imaginary parts are positive,and q4P ,q5P,and q6P denote those whose imaginary parts are negative. Here,q3P corresponds to the electric potential component wave mode,and q1P and q2P correspond to the propagating qP mode and qS mode of wave propagation, respectively. The reflection and refraction coefficients for such an interface are found for two sub cases.Case 1 Open interface
In this case,the boundary conditions (20a)-(20d) are used,which gives AP1X = BP1,where X = [U1,U2,U3,U2f]T,BP1 = [D′14,0,D′34,0]TU1f,and the matrix AP1 is given as

When the fluid-piezoelectric interface is short circuited,the boundary conditions (20a)- (20c) and (20e) are applicable,and the corresponding system is obtained as AP2X=BP2,where X=[U1,U2,U3,U2f]T,BP2=[D′14,0,D′34,0]TU1f,and the matrix AP2 is given by

(vi) Fluid-thermoelastic solid interface
If we set η31 = η15 = η33 = ε11 = ε33 = p3 = 0,the results of the PTHS reduce to those of the thermoelastic half-space. The Christoffel equation for the thermoelastic material becomes
where T1T,T2T ,T3T ,and T4T are given in Appendix E. q1T,q2T,and q3T correspond to the roots of Eq. (35) whose imaginary parts are positive,and q4T ,q5T,and q6T denote those whose imaginary parts are negative. Here,q3T corresponds to the thermal mode,and q1T and q2T correspond to the propagating qP mode and qS mode of wave propagation,respectively. The reflection and refraction coefficients for such an interface are found for two sub cases.Case 1 Isothermal interface
In this case,the boundary conditions (20a)-(20c) and (20f) are used,which give AT1X = BT1,where X = [U1,U2,U3,U2f]T,BT1 = [M14,0,M34,0]TU1f,and the matrix AT1 is given as

When the fluid-thermoelastic interface is adiabatic (thermally insulated),the boundary conditions (20a)-(20c) and (20g) are applicable,and the corresponding system is obtained as AT2X = BT2,where X = [U1,U2,U3,U2f]T,BT2 = [M14,0,M34,0]TU1f,and the matrix AT2 is given by

(vii) Fluid-elastic solid interface
In the absence of piezoelectric,pyroelectric,and thermal effects,Eq.(10) reduces to
where T1E,T 2E,and T3E are given in Appendix F. q1E and q2E correspond to the roots of this equation whose imaginary parts are positive,and q3E and q4E denote those whose imaginary parts are negative. Here,q1E and q2E correspond to the P mode and S mode of wave propagation,respectively. In this case,the boundary conditions (20a)-(20c) are applicable,and then we obtain the non-homogeneous system AEX = BE,where X = [U1,U2,U2f]T,BE= [E13,0,E33]TU1f,and the matrix AE is given by

The amplitude and energy ratios for reflected and transmitted waves are calculated for a particular model CdSe and water. The elastic,dielectric,piezoelectric,thermal,and pyroelectric coefficients,followed from Sharma et al.[40] and Vashishth and Gupta[46],are listed in Tables 1 and 2. The PTHS is loaded with water.
 |
 |
Figure 2 shows the variation of reflected and transmitted amplitude ratios with the angle of incidence (θ) of compressional wave propagating in the fluid medium at the frequency ω = 2π×1012 Hz and the relaxation time τo=10-12 s and τ1=3×10-12 s using two different theories LS and GL of thermoelasticity. Both theories almost show the same behaviour except at θ = 26° in the case of transmitted PE1 mode,where the value of amplitude ratio is less in the case of the GL theory in comparison to the LS theory. Figure 3 depicts the variation of reflected and transmitted amplitude ratios under isothermal open and isothermal short boundary conditions. In the case of isothermal open boundary conditions,there is a slight increase in the reflected amplitude ratio at θ = 31°,and the amplitude ratio of transmitted qP wave increases from θ = 31° to θ = 59 ° and then decreases up to θ = 81°. The amplitude ratio of transmitted PE1 mode decreases in the case of isothermal short boundary conditions. Figure 4 shows that by changing the boundary conditions from isothermal to adiabatic,the amplitude ratios are not affected,and Fig. 5 shows that in the case of adiabatic open and adiabatic short boundary conditions,the amplitude ratios show the same behaviour as in the case of isothermal open and isothermal short boundary conditions
 |
| Fig. 2. Variation of reflected and transmitted amplitude ratios with angle of incidence (θ) using LS and GL theories,where Ainc and Aref represent amplitudes of incident and reflected waves, and A1,A2,A3,and A4 represent amplitudes of transmitted qP,qS,qT,and PE1 waves |
 |
| Fig. 3. Variation of reflected and transmitted amplitude ratios with angle of incidence (θ) under isothermal open and isothermal short boundary conditions |
 |
| Fig. 4. Variation of reflected and transmitted amplitude ratios with angle of incidence (θ) under isothermal and adiabatic boundary conditions |
 |
| Fig. 5. Variation of reflected and transmitted amplitude ratios with angle of incidence (θ) under adiabatic open and adiabatic short boundary conditions |
From Fig. 6,it is observed that the amplitude ratios are not affected by the change in the values of thermal conductivity from K11 = K33=9 to K11= K33=0.000 1. From Fig. 7,it is observed that,when the value of the specific heat varies from 100 J/(kg·K) to 300 J/(kg·K) and to 800 J/(kg·K),the amplitude ratio of the qP and qT mode decreases. Figures 8 and 9 show that the change in the frequency affects the amplitude ratio slightly,and the change in the relaxation time (τ◦) affects the amplitudes of qP and qT waves slightly.
 |
| Fig. 6. Variation of reflected and transmitted amplitude ratios with angle of incidence (θ) under different values of thermal conductivity (Kij) |
 |
| Fig. 7. Variation of reflected and transmitted amplitude ratios with angle of incidence (θ) under different values of specific heat (Ce) |
 |
| Fig. 8. Variation of reflected and transmitted amplitude ratios with angle of incidence (θ) under different values of frequency (ω) |
 |
| Fig. 9. Variation of reflected and transmitted amplitude ratios with angle of incidence (θ) under different values of relaxation time (τ◦) |
Next,we shall observe the effect of thermoelasticity on the reflected and transmitted amplitude ratios with the angle of incidence in Fig. 10. In the absence of piezoelectricity,there are three modes in the transmitting medium instead of four,as expected theoretically. The amplitude ratio of qT mode is very small. In the absence of thermoelasticity,there are also three modes in the transmitting medium instead of four,as expected theoretically. This is observed from Fig. 11,and in Fig. 12,the effect of elasticity on the reflected and transmitted amplitude ratios with the angle of incidence is observed.
 |
| Fig. 10. Variation of reflected and transmitted amplitude ratios with angle of incidence (θ) under reduced case of piezo-thermoelasticity to thermoelasticity |
 |
| Fig. 11. Variation of reflected and transmitted amplitude ratios with angle of incidence (θ) under reduced case of piezo-thermoelasticity to piezoelecticity |
 |
| Fig. 12. Variation of reflected and transmitted amplitude ratios with angle of incidence (θ) under reduced case of piezo-thermoelasticity to elasticity |
The energy ratios of reflected wave,transmitted waves,and interaction energy coefficients are computed using Eqs. (26)-(29). Figure 13 shows the variation of energy ratios with the angle of incidence (θ) of compressional wave propagating in the fluid medium at the frequency=2π× 1012 Hz. The energy ratios corresponding to reflected and transmitted waves are represented by Eref and Es (s = 1,2,· · · ,4),respectively. The total interaction energy ratio between the transmitted waves is denoted by Eint. It is observed that before θ = 25°,all the transmitted wave modes,namely,PE1,qP,qS,and qT,propagate in the PTHS,and after θ=25°,the transmitted qP wave mode is no longer excited. Between θ = 25° and θ = 76°,two modes, i.e.,qS and qT,propagate in the PTHS,and after θ = 76°,only quasi thermal mode is excited. The energy carried out by the electric potential components PE1 is very small. The contribution of interaction energy ratio between the transmitted waves is almost negligible except at θ = 26° and from θ = 74° to θ = 86°. For a compressional wave,incident from the fluid medium,there are two critical angles θ1 = 25° and θ2 = 76° corresponding to transmitted P wave and S wave in the PTHS,respectively. Beyond the second critical angle,i.e., θ=76°,the incident wave is totally reflected,and the energy reflection coefficient equals unity.
 |
| Fig. 13. Variation of reflected and transmitted energy ratios with angle of incidence (θ) using LS and GL theories |
In the case of a perfect elastic medium,i.e.,for a lossless medium,the transmitted wave decays with distance from the interface for supercritical incidence[47]. However,for a medium with loss,it is possible to have transmitted waves whose amplitude grows with distance from the interface for some angles of incidence beyond critical angle as in viscoelasticity,critical angles for transmitted wave are isolated[47, 48]. For anelastic reflection-refraction problems,contrasts in anelastic absorption at a boundary give rise to inhomogeneous waves for all angles of incidence as opposed to the elastic reflection-refraction problems where inhomogeneous wave exists only beyond critical angles[49]. The major portion of incident energy is reflected back,which signifies the fact that the transmitting medium is much denser. The results are in agreement with the law of conservation of energy. There is no null in reflection coefficient which reveals the effect of transversely anisotropy[50].
Figure 14 shows the variation of energy ratios for isothermal short and isothermal open boundary conditions. The angles of incidence,where the energy ratios for the isothermal short boundary are greater than those for the open boundary,are 76°,71°,and 39°,respectively. For all other angles of incidence,no noticeable difference between the results for these two cases is observed. The energy ratio of PE1 mode increases after θ = 31° in the case of isothermal open boundary conditions,and the modulus of interaction energy increases in the case of isothermal short boundary conditions. Figure 15 depicts that,when we compare isothermal and adiabatic conditions,the energy ratio of qT wave and the interaction energy ratio increase in the case of adiabatic conditions. Now,in comparison with adiabatic open and adiabatic short conditions in Fig. 16,we find that the energy ratios of qP and qT waves and the interaction energy ratio increase in the case of adiabatic short boundary conditions,and the energy ratio of PE1 mode decreases in the case of adiabatic short boundary conditions. Figure 17 depicts that the thermal conductivity has no effect on the energy ratios,while the interaction energy ratio slightly increases with the increase in the values of thermal conductivity constants.
 |
| Fig. 14. Variation of reflected and transmitted energy ratios with angle of incidence (θ) under isothermal open and isothermal short boundary conditions |
 |
| Fig. 15. Variation of reflected and transmitted energy ratios with angle of incidence (θ) under isothermal and adiabatic boundary conditions |
 |
| Fig. 16. Variation of reflected and transmitted energy ratios with angle of incidence (θ) under adiabatic open and adiabatic short boundary conditions |
 |
| Fig. 17. Variation of reflected and transmitted energy ratios with angle of incidence (θ) under different values of thermal conductivity (Kij) |
Figure 18 depicts that the increase in Ce shifts the critical angle of qP wave,and the energy ratio of PE1 mode decreases with the increase in the values of Ce. From Fig. 19,we can say that the change in the value of ω slightly affects the energy ratios of qT and PE1 wave modes and the interaction energy ratios. Figure 20 gives the information that the energy ratio of PE1 mode and the interaction energy ratio increase with the increase in the thermal relaxation time. Figure 21 gives the information about what happens when the piezo-thermoelastic model changes to the thermoelastic model,and from Fig. 22,we note that the energy ratio of PE1 mode is zero when the piezo-thermoelastic model changes to the piezoelectric model. Figure 23 gives the same result as in Ref. [51],when we take data for aluminium as in this paper.
 |
| Fig. Variation of reflected and transmitted energy ratios with angle of incidence (θ) under different values of specific heat (Ce) |
 |
| Fig. 19. Variation of reflected and transmitted energy ratios with angle of incidence (θ) under different values of frequency (ω) |
 |
| Fig. 20. Variation of reflected and transmitted energy ratios with angle of incidence (θ) under different values of relaxation time (τ◦) |
 |
| Fig. 21. Variation of reflected and transmitted energy ratios with angle of incidence (θ) under reduced case of piezo-thermoelasticity to thermoelasticity |
 |
| Fig. 22. Variation of reflected and transmitted energy ratios with angle of incidence (θ) under reduced case of piezo-thermoelasticity to piezoelecticity |
 |
| Fig. 23. Variation of reflected and transmitted energy ratios with angle of incidence (θ) under reduced case of piezo-thermoelasticity to elasticity |
Some observations from the numerical example lead to the following conclusions.
(i) The reflection and transmission of waves from an interface separating the FHS and the PTHS are studied in the present paper. The analytical expressions for the reflected and transmitted amplitudes and the energy ratios are derived.
(ii) The incident wave is totally reflected,and the energy reflection coefficient equals unity after θ = 76°.
(iii) The resultant interaction energy flux and the energy flux corresponding to the electric potential wave mode are less significant in comparison to those of propagating qP,qS,and qT modes. The results are in agreement with the law of conservation of energy.
(iv) There is no null in the reflection coefficient as expected in the case of transversely isotropy.
(v) The change in frequency does not affect significantly the value of critical angle. Appendix A
where κ = 1 for the LS theory,and κ = 2 for the GL theory of thermoelasticity. Appendix B
For the LS theory,i.e.,for κ = 1,
where in which and For κ=2,i.e.,for the GL theory, where α1,α2,· · · ,α10 are the same as in Eq. (B2),and in which y1,y2,· · · ,y12 and x1,x2,· · · ,x6 are the same as in Eqs. (B3) and (B4),respectively,and Appendix Cwhere Appendix D
where in which Also, Appendix E
where in which Also, Appendix F
where Also,
| [1] | Cady, W. G. Piezoelectricity, McGraw-Hill, New York (1946) |
| [2] | Auld, B. A. Acoustic Field and Waves in Solids, Vol. II, Wiley InterScience, New York, 423 (1973) |
| [3] | Auld, B. A. Acoustic Fields and Waves in Solids, Vol. I, Keieger Publishing Company, Malabar, Florida (1990) |
| [4] | Ikeda, T. Fundamentals of Piezoelectricity, Oxford University Press, New York, 65-66 (1996) |
| [5] | Arnau, A. Piezoelectric Transducers and Applications, 1st ed., Springer, New York (2004) |
| [6] | Arnau, A. Piezoelectric Transducers and Applications, 2nd ed., Springer, New York (2008) |
| [7] | Knott, C. G. Reflection and refraction of elastic waves with seismological applications. Philosophical Magazine, 48, 64-97 (1899) |
| [8] | Crampin, S. and Taylor, D. B. The propagation of surface waves in anisotropic media. Geophysical Journal of the Royal Astronomical Society, 25, 71-87 (1971) |
| [9] | Crampin, S. Distinctive particle motion of surface waves as a diagnostic of anisotropic layering. Geophysical Journal of the Royal Astronomical Society, 40, 177-186 (1975) |
| [10] | Achenbach, J. D. Wave Propagation in Elastic Solids, North Holland Pub., Amsterdam (1973) |
| [11] | Pal, A. K. and Chattopadhyay, A. The reflection phenomenon of plane waves at a free boundary in a pre-stressed elastic half-space. Journal of the Acoustical Society of America, 76(3), 924-925 (1984) |
| [12] | Borejko, P. Reflection and transmission coefficients for three-dimensional plane waves in elastic media. Wave Motion, 24, 371-393 (1996) |
| [13] | Ogden, R. W. and Sotirropoulos, D. The effect of pre-stress on the propagation and reflection of plane waves in incompressible elastic solids. IMA Journal of Applied Mathematics, 59, 95-121 (1997) |
| [14] | Ogden, R. W. and Sotirropoulos, D. Reflection of plane wave from the boundary of a pre-stressed compressible elastic half-space. IMA Journal of Applied Mathematics, 61, 61-90 (1998) |
| [15] | Chattopadhyay, A. and Rogerson, G. A.Wave reflection in slightly compressible, finitely deformed elastic media. Archive of Applied Mechanics, 71, 307-316 (2001) |
| [16] | Chattopadhyay, A. Wave reflection in triclinic crystalline medium. Archive of Applied Mechanics, 76, 65-74 (2006) |
| [17] | Deschamps, M. Reflection and refraction of the evanescent plane wave on plane interfaces. Journal of the Acoustical Society of America, 96, 2841-2848 (1991) |
| [18] | Lord, H. W. and Shulman, Y. A generalized dynamical theory of thermoelasticity. Journal of the Mechanics and Physics of Solids, 15, 299-309 (1967) |
| [19] | Green, A. E. and Lindsay, K. A. Thermoelasticity. Journal of Elasticity, 2, 1-7 (1972) |
| [20] | Deresiewicz, H. Effect of boundaries on waves in a thermoelastic solid: reflection of plane wave from plane boundary. Journal of the Mechanics and Physics of Solids, 8, 164-172 (1960) |
| [21] | Sinha, A. N. and Sinha, S. B. Reflection of thermoelastic waves at a solid half-space with thermal relaxation. Journal of Physics of the Earth, 22, 237-244 (1974) |
| [22] | Singh, B. Reflection of plane sound wave from a micropolar generalized thermoelastic solid half-space. Journal of Sound and Vibration, 235, 685-696 (2000) |
| [23] | Sinha, S. B. and Elsibai, K. A. Reflection and refraction of thermoelastic wave at an interface of two semi-infinite media with two thermal relaxation times. Journal of Thermal Stresses, 20, 129-146 (1997) |
| [24] | Abd-Alla, A. N. and Al-Dawy, A. S. The reflection phenomenon of SV waves in a generalized thermoelastic medium. International Journal of Mathematics and Mathematical Sciences, 23, 529-546 (2000) |
| [25] | Sharma, J. N., Kumar, V., and Chand, D. Reflection of generalized thermoelastic wave from the boundary of a half-space. Journal of Thermal Stresses, 26, 925-942 (2003) |
| [26] | Deschamps, M. and Cheng, C. Liquid-thermoviscoelastic solids interface. Ultrasonics, 27, 308-313 (1989) |
| [27] | Parton, V. Z. and Kudryavtsev, B. A. Electromagnetoelasticity, Piezoelectrics and Electrically Conductive Solids, Gorden and Breach, New York, 503 (1988) |
| [28] | Noorbehesht, B. and Wade, G. Spatial frequency characteristics of opto-acoustic transducers. Acoustical Imaging (ed. Wang, K. Y.), Vol. 9, Plenum, New York, 139-154 (1980) |
| [29] | Noorbehesht, B. and Wade, G. Reflection and transmission of plane elastic waves at the boundary between piezoelectric materials and water. Journal of the Acoustical Society of America, 67(6), 1947-1953 (1980) |
| [30] | Nayfeh, A. D. and Chien, H. T. The influence of piezoelectricity on free and reflected waves from fluid loaded anisotropic plates. Journal of the Acoustical Society of America, 91(3), 1250-1261 (1992) |
| [31] | Nayfeh, A. D. and Chien, H. T. Wave propagation interaction with free and fluid loaded piezo-electric substrates. Journal of the Acoustical Society of America, 91(6), 3126-3135 (1992) |
| [32] | Mindlin, R. D. On the equations of motion of piezoelectric crystals. Problem of Continuum 290 Mechanics (ed. Muskhelishvili, N. I.), 70th Birthday Volume, SIAM, Philadelphia, 282-290 (1961) |
| [33] | Mindlin, R. D. Equations of high frequency vibrations of thermopiezoelectric crystal plates. International Journal of Solids and Structures, 10, 625-637 (1974) |
| [34] | Nowacki, W. Some general theorems of thermopiezoelectricity. Journal of Thermal Stresses, 1, 171-182 (1978) |
| [35] | Chandrasekharairh, D. S. A temperature rate dependent theory of thermoelasticity. Journal of Thermal Stresses, 7, 293-306 (1984) |
| [36] | Sharma, J. N. and Pal, M. Propagation of Lamb waves in a transversely isotropic piezothermoe-lastic plate. Journal of Sound and Vibration, 270, 587-610 (2004) |
| [37] | Sharma, J. N., Kumar, V., and Chand, D. Reflection of generalized thermoelastic waves from boundary of a half space. Journal of Thermal Stresses, 26, 925-942 (2003) |
| [38] | Sharma, J. N., Walia, V., and Gupta, S. K. Effect of rotation and thermal relaxation on Rayleigh waves in piezothermoelastic half space. International Journal of Mechanical Sciences, 50(3), 433-444 (2008) |
| [39] | Sharma, M. D. Propagation of inhomogeneous waves in anisotropic piezo-thermoelastic media. Acta Mechanica, 25, 307-318 (2010) |
| [40] | Sharma, J. N., Walia, V., and Gupta, S. K. Reflection of piezothermoelastic waves from the charge and stress free boundary of a transversely isotropic half space. International Journal of Engineering Science, 46, 131-146 (2008) |
| [41] | Mott, G. Reflection and refraction coefficients at a fluid-solid interface. Journal of the Acoustical Society of America, 50, 819-829 (1970) |
| [42] | Singh, B. Plane waves in a thermally conducting viscous liquid. Sadhna, 29(1), 27-34 (2004) |
| [43] | Vashishth, A. K. and Sharma, M. D. Reflection and refraction of acoustic waves at poroelastic ocean bed. Earth Planet Space, 61, 675-687 (2009) |
| [44] | Scott, N. H. Energy and dissipation of inhomogeneous plane waves in thermoelasticity. Wave Motion, 23, 393-406 (1996) |
| [45] | Kuang, Z. B. and Yuan, X. G. Reflection and transmission of waves in pyroelectric and piezoelectric materials. Journal of Sound and Vibration, 330, 1111-1120 (2011) |
| [46] | Vashishth, A. K. and Gupta, V. Reflection and transmission of plane waves from a fluid-porous piezoelectric solid interface. Journal of the Acoustical Society of America, 129(6), 3690-3701 (2011) |
| [47] | Krebes, E. S. The viscoelastic reflection/transmission problem: two special cases. Bulletin of the Seismological Society of America, 73(6), 1673-1683 (1983) |
| [48] | Stoll, R. D. and Kan, T. K. Reflection of acoustic waves at a water-sediment interface. Journal of the Acoustical Society of America, 70, 149-156 (1981) |
| [49] | Borcherdt, R. D., Glassmoyer, G., and Wennerberg, L. Influence of welded boundaries in anelastic media on energy flow, and characterestics of P, S-I and S-II waves: observational evidence for inhomogeneous body waves in low-loss solids. Journal of Geophysical Research, 91(B11), 11503-11518 (1986) |
| [50] | Ankan, O., Telatar, E., and Atalar, A. Reflection coefficient null of acoustic waves at a liquid-anisotropic solid interface. Journal of the Acoustical Society of America, 85(1), 1-10 (1989) |
| [51] | Mayer, G. W. Reflection and refraction of mechanical waves at solid liquid boundaries. Journal of Applied Physics, 34, 909-912 (1963) |
 2015, Vol. 36
2015, Vol. 36




























































