1 Introduction
The flow of viscous fluid in channel with porous walls has been investigated by many researchers for different physical situations. In such a system,the consideration of thermal effects
and thermal stability criteria ought to be a major part of the analysis. Various applications
are found in geothermal energy extraction,drying of food,nuclear waste disposal,heat and
fluid exchange inside human organs,insulation of building,groundwater movement,oil and
gas production,surface catalysis of chemical reactions,regenerative heat exchange and adsorption,etc. In some of these physical systems,the fluids involved belong to the wide class of
non-Newtonian fluids due to their failure in obeying the classical linear viscosity model. Thus,
many researchers
[1,2,3,4,5]
discussed the viscous fluid situation. The flow due to a stretching sheet
has applications in continuous casting of metals,glass blowing,and spinning of synthetic fibers.
Due to such applications,Crane
[6]
initiated the flow due to a linear stretching sheet. Many
authors extended the work of Ref. [6] to both viscous and non-Newtonian flows with different
boundary conditions. Gupta and Gupta
[7]
discussed heat transfer from an isothermal stretching sheet with suction/blowing effects. Chen and Char
[8]
extended the work of Ref. [7] to that
of a non-isothermal stretching sheet. Grubka and Bobba
[9]
carried out heat transfer analysis by considering the power-law variation of surface temperature. Chiam
[10]
investigated the magnetohydrodynamic (MHD) heat transfer over a non-isothermal stretching sheet. Series solutions of MHD peristaltic flow of a Jeffrey fluid in eccentric cylinders were discussed by Ellahi et
al.
[11]
. Sheikholeslami et al.
[12]
discussed the effects of the MHD for Cu-water nanofluid flow and
heat transfer by the control volume finite element method (CVFEM). Recently,Hayat et al.
[13]
discussed the unsteady flow of third grade fluid over a stretching surface with heat and mass
transfer. The stagnation-point flow of nanofluid towards a stretching sheet was investigated
by Mustafa et al.
[14]
. Hayat et al.
[15]
discussed the effect of the magnetic field on a peristaltic
flow of a second-order fluid in a symmetric channel. Thermal analysis of the flow saturating
porous media over a porous stretching plate was investigated by Tamayol et al.
[16]
. Makinde
and Aziz
[17]
investigated the boundary layer flow of viscous nanofluid past a stretching sheet
with a convective boundary condition. Ellahi and Hameed
[18]
discussed numerical analysis of
steady non-Newtonian fluids with heat transfer,MHD,and nonlinear slip effects. Ellahi
[19]
reported a review for thermodynamics,stability,applications,and techniques of differential types
of fluid.
The squeezing flow between two parallel boundaries is an interesting topic of research due
to its abundant applications. Examples of such flows are quite prevalent in polymer processing,compression and injection modelling. The lubrication system can be discussed through
the squeezing flow. The initial work on the squeezing flow was investigated by Stefan
[20]
. Following Stefan’s work,many researchers investigated such flows through different geometries.
Recently,Hayat et al.
[21]
discussed the MHD squeezing flow of second grade fluid between two
parallel plates. The unsteady squeezing flow of a Jeffrey fluid between parallel disks was investigated by Qayyum et al.
[22]
. Mustafa et al.
[23]
reported heat and mass transfer characteristics
squeezing flow of viscous fluid. Domairry and Aziz
[24]
developed the homotopy perturbation
solution (HPS) for MHD squeezed flow between the parallel disks. The three-dimensional
squeezing flow in a rotating channel of lower stretching porous wall was discussed by Munawar
et al.
[25]
.
In this attempt,we extend the work of Ref. [25] for mixed convection flow in presence of
thermal radiation. We also consider the viscous dissipation effects. Such a consideration is
significant,because the viscous dissipation effects (the generation of heat due to friction caused
by shear in the flow) are important when the fluid is largely viscous or flowing at a high speed.
The structure of this article is as follows. The problem development is given in Section 2. In
Section 3,the solution is computed by the modern technique known as the homotopy analysis
method (HAM)
[26,27,28,29,30,31,32]
. Section 4 contains the convergence analysis. Results and discussion are
presented in Section 5.
2 Problem development
Let us consider an unsteady incompressible three-dimensional mixed convection rotating flow
of viscous fluid between two infinite vertical plane walls. The fluid is electrically conducting.
The plane (positioned at y = 0) is stretched with a time-dependent velocity U0(t) =
 in
the x-direction. The plane is located at a variable distance
in
the x-direction. The plane is located at a variable distance  and it squeezes
the fluid with a time dependent velocity
and it squeezes
the fluid with a time dependent velocity  in the negative y-direction. The fluid and
the channel are rotating about the y-axis with an angular velocity
in the negative y-direction. The fluid and
the channel are rotating about the y-axis with an angular velocity  and the plate
y = 0 sucks the flow with a velocity
and the plate
y = 0 sucks the flow with a velocity  A magnetic field
A magnetic field  is applied along the y-axis.
The viscous dissipation effects are also considered. The flow configuration and the coordinate
system are shown in Fig. 1. The governing equations for the velocity and temperature fields are
as follows:
is applied along the y-axis.
The viscous dissipation effects are also considered. The flow configuration and the coordinate
system are shown in Fig. 1. The governing equations for the velocity and temperature fields are
as follows:
Here,
u,v,and
w are the velocity components in the
x-,
y- and
z-directions,respectively.
ρ is
the fluid density,
ν is the kinematic viscosity,
p is the pressure,
T is the fluid temperature,
g is the magnitude of acceleration due to gravity,
µ is the dynamic viscosity,
cp
is the specific heat
at constant pressure,
k is the coefficient of thermal conductivity,
B0
is the magnetic field,and
γ is the characteristic parameter.
The boundary conditions are
where
a is the stretching rate of the wall
y = 0,and
V0 is the suction/injection velocity. Substituting
into Eqs. (2)-(5),we have
with the boundary conditions
where the squeezing parameter
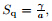
,the suction/injection parameter
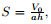
,the Prandtl
number
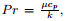
,the magnetic parameter
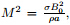
the rotation parameter
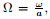
the
mixed convection parameter
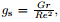
the modified Grashaf number
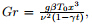
and the
Reynolds number
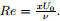
Note that the plane at
y =
h(t) moves with the velocity
Vh < 0
for
Sq > 0 towards the plane at
y = 0. For
Sq < 0,the plane at
y =
h(t) moves apart with
respect to the plane
y = 0,and
Sq
= 0 corresponds to the steady case or the stationary plane. The skin friction coefficient and the Nusselt number are defined as
where
In terms of dimensionless variables (7) in (12),we get
3 Homotopy analysis solutions
3.1 Zeroth-order deformation problems
The initial guess F0,G0,θ0,and the auxiliary linear operators LF,LG,and Lθ
are defined as follows:
with
where
Ci (
i = 1,2,· · · ,8) are the arbitrary constants. The nonlinear operators are
The zeroth-order deformation problems are
where
 F
F ,
 G
G ,and
 θ
θ
are the auxiliary parameters,and
p ∈
[0,1] is an embedding parameter.
Note that,when p changes from 0 to 1,
F(
η,p) varies from
F0(η) to
F (η) ,
G(
η,p) varies from
G0(η) to
G(η),and
θ(
η,p) varies from
θ0(η) to
θ(η). When
p = 0 and
p = 1,one obtains
In view of the Taylor series,we can write
The convergence of the series solution is dependent upon
 F
F ,
 G
G ,and
 θ
θ
. We choose
 F
F ,
 G
G ,
and
 θ
θ in such a way that the series (32)-(34) converge at
p = 1 and hence
3.2 mth-order deformation problems
The mth-order deformation equations are obtained by differentiating Eqs. (25)-(27) m times
with respect to p and then setting p = 0,which are
The general solution to Eqs. (38)-(40) can be expressed as
in which
Fm*,
Gm*,and
θm* epresent the special solutions.
3.3 Convergence analysis
The series solutions (38)-(40) contain the auxiliary parameters  F ,
F , G ,and
G ,and  θ
. These parameters adjust the convergence of the obtained series solutions.Figures 2-4 show the
θ
. These parameters adjust the convergence of the obtained series solutions.Figures 2-4 show the  -curves of the functions F,G,and θ for suction. The permissible values of these auxiliary
parameters
-curves of the functions F,G,and θ for suction. The permissible values of these auxiliary
parameters  F,
F, G ,and
G ,and  θ
are −1.3 6 (
θ
are −1.3 6 ( F,
F, G ) 6 −0.3 and −1.2 6
G ) 6 −0.3 and −1.2 6  θ 6 −0.4. Table 1
is useful in making a guess of what order of approximations are necessary for a convergent
solutions. This table shows that the 25th-order of approximations is enough for the convergent
solutions for suction.
θ 6 −0.4. Table 1
is useful in making a guess of what order of approximations are necessary for a convergent
solutions. This table shows that the 25th-order of approximations is enough for the convergent
solutions for suction.
Table 1 Convergence of HAM solutions for different orders of approximations when Sq = M = Ω = Ec = Re = gs = 1.0 and S = Pr = 0.5
We also use MATHEMATICA package BVPh 2.0 to solve the coupled nonlinear ODEs
(8)-(10) with the boundary conditions (11). We use BVPh
[11,15]
to obtain the 15th-order of
approximations for the momentum and energy equations. The minimum squared residual errors
at 15th-order of approximations are 3.237 5 × 10−23
,4.936 58 × 10−25,and 1.697 41 × 10−23 for
F,G,and θ,respectively. Figure 5 is sketched for the solutions of F,G,and θ. Figure 6 shows the total residual errors corresponding to different orders of approximations.
5 Results and discussion
To investigate the effects of different parameters on the flow and heat transfer,Figs. 7-14
are plotted. The velocity and temperature profiles against η are plotted for different values of
the involved parameters. The effect of Sq on the velocity component F is investigated in Fig. 7.
It is observed that as Sq
increases,the velocity profile F increases. The effect of the suction
parameter S on the velocity profile F is discussed in Fig. 8. With the increase in S,the velocity
profile F increases. The permeable nature of the right disk allows the fluid particles to move
closer to the boundary,which makes the boundary layer thinner. The effects of the mixed convection parameter gs on the velocity profile F' and F,are shown in Figs. 9 and 10,respectively.
With the increase in the mixed convection parameter gs,the magnitude of the velocity profile
increases for 0 6 η 6 0.5,and it decreases for 0.5 6 η 61. The influence of gs on the velocity component F is plotted in Fig. 10. Here,the velocity field F decreases with the increase in gs . The effect of the squeezing parameter Sq
on the temperature profile θ is observed in Fig. 11. With
the increase in Sq
,the temperature profile decreases,and the thermal boundary thickness also
decreases. The influence of the Prandtl number Pr on the temperature profile θ is displayed
in Fig. 12. Due to the large viscous dissipation effect,the temperature profile shows a rapid
increase by increasing Pr,while the thermal boundary layer thickness decreases with increasing
values of Pr. The effect of the Eckert number Econ the temperature profile θ is observed in
Fig. 13. The effects of Ecand Pr are similar in a quantitative sense. The viscous dissipation
effects are important only when the fluid is very viscous. This phenomenon occurs at high
Eckert number (Ec >> 1). The effect of the mixed convection parameter gs on the temperature profile θ is plotted in Fig. 14. The temperature decreases with the increase in gs. Physically,
the mixed convection parameter depends on the buoyancy force. Therefore,the increase in
the mixed convection parameter means an increase in the buoyancy force. An increase in the
buoyancy force gives rise to the fluid flow by which the velocity increases and the temperature
decreases. Figures 15-19 present the three-dimensional plot of the velocity components of u,v,
and w. Figure 15 shows the effects of x and η on the velocity component u. With the increase
in x,the stretching velocity increases near the left plane and is minimum at the centre of the channel. Figures 16 and 17 show the effects of t and η on the velocity components u and v.
With the increase in t and η,the velocity components u and v increase near the planes but
decrease near the centre of the channel. Figures 18 and Figures 19 indicate the effects of x and t on the
velocity component w. With the increase in x and t,the velocity component w increases at the
centre of the channel.
Tables 2 and 3 are prepared for the numerical values of the skin friction and the Nusselt
number for different parameters. With the increase in the rotation parameter Ω,the suction
parameter S,the magnitude of the skin friction coefficient,and the magnitude of the local
Nusselt number increase, while with the increase in the squeezing parameter Sq
and gs,the
magnitude of the skin friction coefficient and the magnitude of local Nusselt number at the
left plane decrease. However,the behavior of these quantities on the right plane is opposite.
Table 3 shows the effects of Pr,Re,and Ec on the Nusselt number at the left and right planes.
With the increase in Pr and Ec,the magnitude of the Nusselt number increases at the surface
of the right plane and decreases at the surface of the left plane. With the increase in Re,the
magnitude of the Nusselt number decreases at the left plane and increases at the right plane.
Table 4 gives a comparison of the present results with the previous published work. This table
shows that the present results are in excellent agreement with previous results in a limiting
case.
Table 2 Skin friction coefficient and local Nusselt number at both walls for different values of parameters when M = Pr = Ec = Re = 1.0
Table 3 Local Nusselt number at both walls for different values of parameters when S = 0.5 and Sq = M = Ω = gs = 1.0
Table 4 Comparison of shear stresses F′′ (0) and F′′ (1) for different values of suction/injection parameter S when M = 0.5 and gs = 0.0
 in
the x-direction. The plane is located at a variable distance
in
the x-direction. The plane is located at a variable distance  and it squeezes
the fluid with a time dependent velocity
and it squeezes
the fluid with a time dependent velocity  in the negative y-direction. The fluid and
the channel are rotating about the y-axis with an angular velocity
in the negative y-direction. The fluid and
the channel are rotating about the y-axis with an angular velocity  and the plate
y = 0 sucks the flow with a velocity
and the plate
y = 0 sucks the flow with a velocity  A magnetic field
A magnetic field  is applied along the y-axis.
The viscous dissipation effects are also considered. The flow configuration and the coordinate
system are shown in Fig. 1. The governing equations for the velocity and temperature fields are
as follows:
is applied along the y-axis.
The viscous dissipation effects are also considered. The flow configuration and the coordinate
system are shown in Fig. 1. The governing equations for the velocity and temperature fields are
as follows:

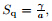 ,the suction/injection parameter
,the suction/injection parameter 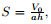 ,the Prandtl
number
,the Prandtl
number 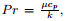 ,the magnetic parameter
,the magnetic parameter 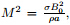 the rotation parameter
the rotation parameter 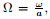 the
mixed convection parameter
the
mixed convection parameter 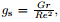 the modified Grashaf number
the modified Grashaf number 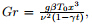 and the
Reynolds number
and the
Reynolds number 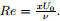 Note that the plane at y = h(t) moves with the velocity Vh < 0
for Sq > 0 towards the plane at y = 0. For Sq < 0,the plane at y = h(t) moves apart with
respect to the plane y = 0,and Sq
= 0 corresponds to the steady case or the stationary plane. The skin friction coefficient and the Nusselt number are defined as
where
In terms of dimensionless variables (7) in (12),we get
3 Homotopy analysis solutions
3.1 Zeroth-order deformation problems
Note that the plane at y = h(t) moves with the velocity Vh < 0
for Sq > 0 towards the plane at y = 0. For Sq < 0,the plane at y = h(t) moves apart with
respect to the plane y = 0,and Sq
= 0 corresponds to the steady case or the stationary plane. The skin friction coefficient and the Nusselt number are defined as
where
In terms of dimensionless variables (7) in (12),we get
3 Homotopy analysis solutions
3.1 Zeroth-order deformation problems F ,
F , G ,and
G ,and  θ
are the auxiliary parameters,and p ∈ [0,1] is an embedding parameter.
Note that,when p changes from 0 to 1,F(η,p) varies from F0(η) to F (η) ,G(η,p) varies from
G0(η) to G(η),and θ(η,p) varies from θ0(η) to θ(η). When p = 0 and p = 1,one obtains
In view of the Taylor series,we can write
The convergence of the series solution is dependent upon
θ
are the auxiliary parameters,and p ∈ [0,1] is an embedding parameter.
Note that,when p changes from 0 to 1,F(η,p) varies from F0(η) to F (η) ,G(η,p) varies from
G0(η) to G(η),and θ(η,p) varies from θ0(η) to θ(η). When p = 0 and p = 1,one obtains
In view of the Taylor series,we can write
The convergence of the series solution is dependent upon  F ,
F , G ,and
G ,and  θ
. We choose
θ
. We choose  F ,
F , G ,
and
G ,
and  θ in such a way that the series (32)-(34) converge at p = 1 and hence
3.2 mth-order deformation problems
θ in such a way that the series (32)-(34) converge at p = 1 and hence
3.2 mth-order deformation problems F ,
F , G ,and
G ,and  θ
. These parameters adjust the convergence of the obtained series solutions.Figures 2-4 show the
θ
. These parameters adjust the convergence of the obtained series solutions.Figures 2-4 show the  -curves of the functions F,G,and θ for suction. The permissible values of these auxiliary
parameters
-curves of the functions F,G,and θ for suction. The permissible values of these auxiliary
parameters  F,
F, G ,and
G ,and  θ
are −1.3 6 (
θ
are −1.3 6 ( F,
F, G ) 6 −0.3 and −1.2 6
G ) 6 −0.3 and −1.2 6  θ 6 −0.4. Table 1
is useful in making a guess of what order of approximations are necessary for a convergent
solutions. This table shows that the 25th-order of approximations is enough for the convergent
solutions for suction.
θ 6 −0.4. Table 1
is useful in making a guess of what order of approximations are necessary for a convergent
solutions. This table shows that the 25th-order of approximations is enough for the convergent
solutions for suction.

 -curve for function F (η)
-curve for function F (η)
 -curve for function G(η)
-curve for function G(η)
 -curve for function θ(η)
-curve for function θ(η)


















 2015, Vol. 36
2015, Vol. 36





















